Однородный 4-многогранник
В геометрии однородный 4-мерный многогранник (или однородный полихор ) [1] — это 4-мерный многогранник , который является вершинно-транзитивным и ячейки которого являются однородными многогранниками , а грани — правильными многоугольниками .
Существует 47 непризматических выпуклых однородных 4-многогранников. Существует два бесконечных множества выпуклых призматических форм, а также 17 случаев, возникающих как призмы выпуклых однородных многогранников. Существует также неизвестное число невыпуклых звездчатых форм.
История открытия
- Выпуклые правильные многогранники :
- 1852 : Людвиг Шлефли доказал в своей рукописи Theorie der vielfachen Kontinuität , что существует ровно 6 правильных многогранников в 4 измерениях и только 3 в 5 или более измерениях.
- Правильные звездчатые 4-мерные многогранники ( ячейки звездчатых многогранников и/или вершинные фигуры )
- 1852 : Людвиг Шлефли также нашел 4 из 10 правильных звездчатых 4-мерных многогранников, не считая 6 с ячейками или вершинными фигурами { 5 / 2,5 } и {5, 5 / 2 } .
- 1883 : Эдмунд Гесс завершил список 10 невыпуклых правильных 4-многогранников в своей книге (на немецком языке) Einleitung in die Lehre von der Kugelteilung mit besonderer Berücksichtigung ihrer Anwendung auf die Theorie der Gleichflächigen und der gleicheckigen Polyeder Einleitung in die Lehre von. der Kugelteilung mit besonderer Berücksichtigung ihrer Anwendung auf die Theorie der Gleichflächigen und der gleicheckigen Polyeder, von Dr. Эдмунд Хесс. Mit sechzehn литографиртен тафельн..
- Выпуклые полуправильные многогранники : (Различные определения до однородной категории Коксетера )
- 1900 : Торольд Госсет перечислил список непризматических полуправильных выпуклых многогранников с правильными ячейками ( Платоновы тела ) в своей публикации «О правильных и полуправильных фигурах в пространстве n измерений» . В четырех измерениях это дает выпрямленный 5-ячейник , выпрямленный 600-ячейник и плосконосый 24-ячейник . [2]
- 1910 : Алисия Буль Стотт в своей публикации «Геометрическое выведение полуправильных многогранников из правильных многогранников и заполнения пространства » расширила определение, также допустив архимедовы тела и призматические ячейки. Эта конструкция перечислила 45 полуправильных 4-мерных многогранников, соответствующих непризматическим формам, перечисленным ниже. Плосконосый 24-ячейник и большая антипризма отсутствовали в ее списке. [3]
- 1911 : Питер Хендрик Схоуте опубликовал работу «Аналитическое рассмотрение многогранников, регулярно полученных из правильных многогранников» , следуя обозначениям Буля-Стотта, перечисляя выпуклые однородные многогранники по симметрии на основе 5-ячеечных , 8-ячеечных / 16-ячеечных и 24-ячеечных .
- 1912 : Э. Л. Элте независимо расширил список Госсета, опубликовав «Полуправильные многогранники гиперпространств» , многогранники с одним или двумя типами полуправильных граней. [4]
- Выпуклые однородные многогранники :
- 1940 : Поиск был систематически расширен Г. С. М. Кокстером в его публикации «Правильные и полуправильные многогранники» .
- Выпуклые однородные 4-мерные многогранники :
- 1965 : Полный список выпуклых форм был окончательно перечислен Джоном Хортоном Конвеем и Майклом Гаем в их публикации «Четырехмерные архимедовы многогранники» , установленной с помощью компьютерного анализа, добавив только один невитхоффов выпуклый 4-мерный многогранник — большую антипризму.
- 1966 Норман Джонсон завершает докторскую диссертацию «Теория однородных многогранников и сот» под руководством Коксетера, завершая основную теорию однородных многогранников для размерностей 4 и выше.
- В 1986 году Коксетер опубликовал статью «Правильные и полуправильные многогранники II» , в которой был проанализирован уникальный плосконосый 24-ячеечный многогранник и симметрия аномальной большой антипризмы.
- 1998 [5] -2000 : 4-многогранники были систематически названы Норманом Джонсоном и даны в онлайн-индексированном перечислении Джорджа Ольшевского (использованном в качестве основы для этого списка). Джонсон назвал 4-многогранники полихорами, как полиэдры для 3-многогранников, от греческих корней poly («много») и choros («комната» или «пространство»). [6] Названия однородных полихор начинались с 6 правильных полихор с префиксами, основанными на кольцах в диаграммах Коксетера; усечение t 0,1 , стягивание t 0,2 , скручивание t 0,3 , с одинарными кольцевыми формами, называемыми выпрямленными, и би, три-префиксами, добавляемыми, когда первое кольцо находилось на втором или третьем узле. [7] [8]
- 2004 : Доказательство полноты множества Конвея-Гая было опубликовано Марко Мёллером в его диссертации « Пространственный архимедийный многогранник» . Мёллер воспроизвел в своем списке систему именования Джонсона. [9]
- 2008 : Симметрии вещей [10] были опубликованы Джоном Х. Конвеем и содержат первый опубликованный в печати список выпуклых однородных 4-многогранников и многогранников более высокой размерности по семейству групп Коксетера с общими диаграммами вершинных фигур для каждой кольцевой перестановки диаграмм Коксетера — плосконосой, большой антипризмы и дуопризмы — которые он назвал пропризмами для призм произведений. Он использовал свою собственную схему именования ijk -ambo для индексированных кольцевых перестановок за пределами усечения и битунции, и все имена Джонсона были включены в индекс книги.
- Неправильные однородные звездчатые 4-мерные многогранники : (похожи на невыпуклые однородные многогранники )
- 1966 : Джонсон описывает в своей диссертации три невыпуклые однородные антипризмы в 4-мерном пространстве. [11]
- 1990-2006 : В ходе совместных поисков к 2005 году Джонатан Бауэрс и Джордж Ольшевски идентифицировали в общей сложности 1845 однородных 4-мерных многогранников (выпуклых и невыпуклых) [12] , а в 2006 году было обнаружено еще четыре, что в общей сложности составило 1849. Подсчет включает 74 призмы из 75 непризматических однородных многогранников (поскольку это конечное множество — кубическая призма исключена, поскольку она дублирует тессеракт), но не бесконечные категории дуопризм или призм антипризм. [13]
- 2020-2023 : обнаружено 342 новых полихора, в результате чего общее число известных однородных 4-политопов достигло 2191. Полный список не доказан. [13] [14]
Правильные 4-мерные многогранники
Правильные 4-многогранники являются подмножеством однородных 4-многогранников, которые удовлетворяют дополнительным требованиям. Правильные 4-многогранники могут быть выражены символом Шлефли { p , q , r }, имеют ячейки типа { p , q }, грани типа { p }, реберные фигуры { r } и вершинные фигуры { q , r }.
Существование правильного 4-мерного многогранника { p , q , r } ограничивается существованием правильных многогранников { p , q }, которые становятся ячейками, и { q , r }, которые становятся вершинной фигурой .
Существование в качестве конечного 4-мерного многогранника зависит от неравенства: [15]
16 правильных 4-мерных многогранников , обладающих тем свойством, что все ячейки, грани, ребра и вершины конгруэнтны:
- 6 правильных выпуклых 4-мерных многогранников : 5-ячеечный {3,3,3}, 8-ячеечный {4,3,3}, 16-ячеечный {3,3,4}, 24-ячеечный {3,4,3}, 120-ячеечный {5,3,3} и 600-ячеечный {3,3,5}.
- 10 правильных звездчатых 4-мерных многогранников : икосаэдрический 120-ячейниковый {3,5, 5 / 2 }, малый звездчатый 120-ячейниковый { 5 / 2,5,3 }, большой 120-ячейниковый {5, 5 / 2,5 }, большой 120-ячейниковый {5,3, 5 / 2 }, большой звездчатый 120-ячейниковый { 5 / 2,3,5 }, большой звездчатый 120-ячейниковый { 5 / 2,5 , 5 / 2 }, большой великий 120-ячейниковый {5 , 5 / 2,3 }, большой икосаэдрический 120-ячейниковый {3, 5 / 2,5 }, большой 600-ячейниковый {3,3, 5 / 2 } и большой великий звездчатый 120-ячейниковый { 5 / 2 ,3,3}.
Выпуклые однородные 4-мерные многогранники
Симметрия однородных 4-мерных многогранников в четырех измерениях
24 зеркала F 4 можно разложить на 2 ортогональные группы D 4 :
|
10 зеркал B 3 × A 1 можно разложить на ортогональные группы 4 A 1 и D 3 :
|
Существует 5 фундаментальных семейств точечных групп зеркальной симметрии в 4-мерном пространстве: A 4 =
, В 4 =
, Д 4 =
, Ф 4 =, Н 4 =
. [7] Также существуют 3 призматические группы A 3 A 1 =
, В 3 А 1 =, Н 3 А 1 =и дуопризматические группы: I 2 (p)×I 2 (q) =
Каждая группа определяется фундаментальной областью тетраэдра Гурса, ограниченной зеркальными плоскостями.
Каждый отражающий однородный 4-многогранник может быть построен в одной или нескольких отражающих точечных группах в 4 измерениях с помощью конструкции Витхоффа , представленной кольцами вокруг перестановок узлов на диаграмме Коксетера . Зеркальные гиперплоскости могут быть сгруппированы, как видно по цветным узлам, разделенным четными ветвями. Группы симметрии вида [a,b,a] имеют расширенную симметрию, [[a,b,a]], удваивающую порядок симметрии. Сюда входят [3,3,3], [3,4,3] и [ p ,2, p ]. Однородные многогранники в этих группах с симметричными кольцами содержат эту расширенную симметрию.
Если все зеркала заданного цвета не окольцованы (неактивны) в заданном однородном многограннике, он будет иметь конструкцию с более низкой симметрией, удаляя все неактивные зеркала. Если все узлы заданного цвета окольцованы (активны), операция чередования может сгенерировать новый 4-многогранник с хиральной симметрией, показанный как «пустые» обведенные узлы», но геометрия, как правило, не настраивается для создания однородных решений.
Группа Вейля | Кватернион Конвея | Абстрактная структура | Заказ | Диаграмма Коксетера | нотация Коксетера | Подгруппа коммутатора | Число Кокстера (ч) | Зеркала m =2 ч | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Неприводимый | ||||||||||||
| А 4 | +1/60[I×I].21 | С 5 | 120 | |  | [3,3,3] | [3,3,3] + | 5 | 10 | |||
| Д 4 | ±1/3[T×T].2 | 1/2. 2 С 4 | 192 |  |  | [3 1,1,1 ] | [3 1,1,1 ] + | 6 | 12 | |||
| Б 4 | ±1/6[O×O].2 | 2 С 4 = С 2 ≀С 4 | 384 | |  | [4,3,3] | 8 | 4 | 12 | |||
| Ф 4 | ±1/2[O×O].2 3 | 3. 2 С 4 | 1152 | | | [3,4,3] | [3 + ,4,3 + ] | 12 | 12 | 12 | ||
| Н 4 | ±[I×I].2 | 2.(А 5 ×А 5 ).2 | 14400 | | | [5,3,3] | [5,3,3] + | 30 | 60 | |||
| Призматические группы | ||||||||||||
| А 3 А 1 | +1/24[O×O].2 3 | С 4 × Д 1 | 48 | |  | [3,3,2] = [3,3]×[ ] | [3,3] + | - | 6 | 1 | ||
| Б 3 А 1 | ±1/24[O×O].2 | С 4 × Д 1 | 96 | | | [4,3,2] = [4,3]×[ ] | - | 3 | 6 | 1 | ||
| Н 3 А 1 | ±1/60[I×I].2 | А 5 × Д 1 | 240 | | | [5,3,2] = [5,3]×[ ] | [5,3] + | - | 15 | 1 | ||
| Дуопризматические группы (используйте 2p,2q для четных целых чисел) | ||||||||||||
| Я 2 ( п )Я 2 ( д ) | ±1/2[D 2 p ×D 2 q ] | D п ×D д | 4 пк | | | [ п ,2, q ] = [ п ]×[ q ] | [ п + ,2, д + ] | - | п | д | ||
| Я 2 ( 2п )Я 2 ( д ) | ±1/2[D 4 p ×D 2 q ] | D 2 п ×D q | 8 пк |  | | [2 п ,2, q ] = [2 п ]×[ q ] | - | п | п | д | ||
| Я 2 ( 2п )Я 2 ( 2к ) | ±1/2[D 4 p ×D 4 q ] | Д2п × Д2q | 16 шт. | |  | [2 п ,2,2 q ] = [2 п ]×[2 q ] | - | п | п | д | д | |
Перечисление
Существует 64 выпуклых однородных 4-мерных многогранника, включая 6 правильных выпуклых 4-мерных многогранников и исключая бесконечные множества дуопризм и антипризматических призм .
- 5 — многогранные призмы, основанные на Платоновых телах (1 перекрывается с правильной, поскольку кубическая гиперпризма является тессерактом )
- 13 — многогранные призмы, основанные на архимедовых телах
- 9 относятся к самодвойственной регулярной группе A 4 [3,3,3] ( 5-клеточной ).
- 9 относятся к самодвойственной регулярной группе F 4 [3,4,3] ( 24-клеточной ) семье. (Исключая курносую 24-клеточную)
- 15 из них относятся к обычной группе B 4 [3,3,4] ( тессеракт / 16-ячеечное семейство) (3 перекрываются с 24-ячеечным семейством)
- 15 из них относятся к обычной группе H 4 [3,3,5] ( 120-клеточная / 600-клеточная ).
- 1 особая курносая форма в семействе группы [3,4,3] ( 24-клеточная ).
- 1 специальный невитхоффов 4-мерный многогранник, большая антипризма.
- ИТОГО: 68 − 4 = 64
Эти 64 однородных 4-многогранника проиндексированы ниже Джорджем Ольшевским. Повторяющиеся формы симметрии проиндексированы в скобках.
В дополнение к 64 приведенным выше, существуют 2 бесконечных призматических множества, которые порождают все оставшиеся выпуклые формы:
- Набор однородных антипризматических призм - sr{ p ,2}×{ } - Многогранные призмы из двух антипризм .
- Набор однородных дуопризм - { p }×{ q } - декартово произведение двух многоугольников.
А4семья
Пятиклетка имеет диплоидную пентахорическую [3,3,3] симметрию [ 7] порядка 120 , изоморфную перестановкам пяти элементов, поскольку все пары вершин связаны одинаковым образом.
Даны грани (ячейки), сгруппированные в своих местоположениях на диаграмме Кокстера путем удаления указанных узлов.
| # | Имя Имя Боуэрса (и аббревиатура) | Вершинная фигура | Диаграмма Кокстера и символы Шлефли | Количество клеток по местоположению | Количество элементов | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Поз. 3 (5) | Поз. 2 (10) | Поз. 1 (10) | Поз. 0 (5) | Клетки | Лица | Края | Вершины | ||||
| 1 | 5-клеточный пентахорон [7] (ручка) |  |  {3,3,3} | (4) (3.3.3) | 5 | 10 | 10 | 5 | |||
| 2 | Выпрямленный 5-клеточный Выпрямленный пентахорон (рэп) |  | г{3,3,3} | (3) (3.3.3.3) | (2) (3.3.3) | 10 | 30 | 30 | 10 | ||
| 3 | усеченный 5-клеточный усеченный пентахорон (кончик) |  | т{3,3,3} | (3) (3.6.6) | (1) (3.3.3) | 10 | 30 | 40 | 20 | ||
| 4 | Кантеллированный 5-клеточный Малый ромбовидный пентахорон (srip) |  | рр{3,3,3} | (2) (3.4.3.4) | (2) (3.4.4) | (1) (3.3.3.3) | 20 | 80 | 90 | 30 | |
| 7 | усеченный 5-клеточный большой ромбовидный пентахорон (ручка) |  | тр{3,3,3} | (2) (4.6.6) | (1) (3.4.4) | (1) (3.6.6) | 20 | 80 | 120 | 60 | |
| 8 | рунцитоусеченный 5-клеточный призматорогомбатный пентахорон (прип) |  | т 0,1,3 {3,3,3} | (1) (3.6.6) | (2) (4.4.6) | (1) (3.4.4) | (1) (3.4.3.4) | 30 | 120 | 150 | 60 |
| # | Имя Имя Боуэрса (и аббревиатура) | Вершинная фигура | Диаграмма Коксетера и символы Шлефли | Количество клеток по местоположению | Количество элементов | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Поз. 3-0 (10) | Поз. 1-2 (20) | Альт | Клетки | Лица | Края | Вершины | ||||
| 5 | * струйчатый 5-клеточный Малый призматодекахорон (spid) |  | т 0,3 {3,3,3} | (2) (3.3.3) | (6) (3.4.4) | 30 | 70 | 60 | 20 | |
| 6 | * укороченный 5-клеточный Декахорон (дека) |  | 2т{3,3,3} | (4) (3.6.6) | 10 | 40 | 60 | 30 | ||
| 9 | * всеусеченный 5-клеточный Большой призматодекахорон (гиппид) |  | т 0,1,2,3 {3,3,3} | (2) (4.6.6) | (2) (4.4.6) | 30 | 150 | 240 | 120 | |
| Неравномерный | omnisnub 5-клеточный Курносый декахорон (снад) Курносый пентахорон (снип) [16] |  |  хт 0,1,2,3 {3,3,3} |  (2) (3.3.3.3.3) |  (2) (3.3.3.3) | (4) (3.3.3) | 90 | 300 | 270 | 60 |
Три однородные формы 4-многогранников, отмеченные звездочкой , * , имеют более высокую расширенную пентахорическую симметрию , порядка 240, [[3,3,3]], поскольку элемент, соответствующий любому элементу базовой 5-клетки, можно поменять местами с одним из тех, которые соответствуют элементу его двойственной. Существует одна малая подгруппа индексов [3,3,3] + , порядка 60, или ее удвоение [[3,3,3]] + , порядка 120, определяющая всенощную 5-клетку , которая указана для полноты, но не является однородной.
Б4семья
Это семейство имеет диплоидную гексадекахорическую симметрию , [7] [4,3,3], порядка 24×16=384: 4!=24 перестановок четырех осей, 2 4 =16 для отражения по каждой оси. Существует 3 малых подгруппы индексов, причем первые две генерируют однородные 4-многогранники, которые также повторяются в других семействах, [1 + ,4,3,3], [4,(3,3) + ] и [4,3,3] + , все порядка 192.
Усечения Тессеракта
| # | Имя (имя и аббревиатура Bowers) | Вершинная фигура | Диаграмма Кокстера и символы Шлефли | Количество клеток по местоположению | Количество элементов | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
Поз. 3   (8) | Поз. 2 (24) | Поз. 1 (32) | Поз. 0 (16) | Клетки | Лица | Края | Вершины | |||||
| 10 | тессеракт или 8-ячеечный тессеракт (tes) |  | {4,3,3} | (4) (4.4.4) | 8 | 24 | 32 | 16 | ||||
| 11 | Выпрямленный тессеракт (рит) |  | г{4,3,3} | (3) (3.4.3.4) | (2) (3.3.3) | 24 | 88 | 96 | 32 | |||
| 13 | Усеченный тессеракт (тат) |  | т{4,3,3} | (3) (3.8.8) | (1) (3.3.3) | 24 | 88 | 128 | 64 | |||
| 14 | Тессеракт с ромбовидными ярусами. Малый ромбовидный тессеракт (srit) |  | рр{4,3,3} | (2) (3.4.4.4) | (2) (3.4.4) | (1) (3.3.3.3) | 56 | 248 | 288 | 96 | ||
| 15 | Тессеракт с ручьём (также 16-ячеечный с ручьём ) Малый диспризматотессерактигексадекахорон (сидпит) |  | т 0,3 {4,3,3} | (1) (4.4.4) | (3) (4.4.4) | (3) (3.4.4) | (1) (3.3.3) | 80 | 208 | 192 | 64 | |
| 16 | Тессеракт усеченный (также усеченный 16-ячейниковый ) |  | 2т{4,3,3} | (2) (4.6.6) | (2) (3.6.6) | 24 | 120 | 192 | 96 | |||
| 18 | Усеченный тессеракт Большой ромбический тессеракт (зернистость) |  | тр{4,3,3} | (2) (4.6.8) | (1) (3.4.4) | (1) (3.6.6) | 56 | 248 | 384 | 192 | ||
| 19 | Тессеракт с усеченным призматическим рогом, гексадекахорон (proh) |  | т 0,1,3 {4,3,3} | (1) (3.8.8) | (2) (4.4.8) | (1) (3.4.4) | (1) (3.4.3.4) | 80 | 368 | 480 | 192 | |
| 21 | Всеусеченный тессеракт (также всеусеченный 16-клеточный ) Большой диспризматотессерактигексадекахорон (гидпит) |  | т 0,1,2,3 {3,3,4} | (1) (4.6.8) | (1) (4.4.8) | (1) (4.4.6) | (1) (4.6.6) | 80 | 464 | 768 | 384 | |
| # | Название (аббревиатура в стиле Боуэрса) | Вершинная фигура | Диаграмма Кокстера и символы Шлефли | Количество клеток по местоположению | Количество элементов | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Поз. 3 (8) | Поз. 2 (24) | Поз. 1 (32) | Поз. 0 (16) | Альт | Клетки | Лица | Края | Вершины | ||||
| 12 | Половина тессеракта Демитессеракт = 16-ячеечный (гексагональный) |  |  = ч{4,3,3}={3,3,4} | (4) (3.3.3) | (4) (3.3.3) | 16 | 32 | 24 | 8 | |||
| [17] | Кантический тессеракт = усеченный 16-ячейковый (thex) |  | = ч 2 {4,3,3}=т{4,3,3} | (4) (6.6.3) | (1) (3.3.3.3) | 24 | 96 | 120 | 48 | |||
| [11] | Runcic tesseract = Выпрямленный тессеракт (rit) |  | = ч 3 {4,3,3}=р{4,3,3} | (3) (3.4.3.4) | (2) (3.3.3) | 24 | 88 | 96 | 32 | |||
| [16] | Тессеракт Runcicantic = Усеченный битсеракт (tah) |  | = ч 2,3 {4,3,3}=2т{4,3,3} | (2) (3.4.3.4) | (2) (3.6.6) | 24 | 120 | 192 | 96 | |||
| [11] | = Выпрямленный тессеракт (крыса) | |  = ч 1 {4,3,3}=r{4,3,3} | 24 | 88 | 96 | 32 | |||||
| [16] | = Усеченный тессеракт (tah) | | = ч 1,2 {4,3,3}=2т{4,3,3} | 24 | 120 | 192 | 96 | |||||
| [23] | = Выпрямленный 24-элементный (rico) |  | = ч 1,3 {4,3,3}=рр{3,3,4} | 48 | 240 | 288 | 96 | |||||
| [24] | = Усеченный 24-ячеечный (tico) |  | = ч 1,2,3 {4,3,3}=тр{3,3,4} | 48 | 240 | 384 | 192 | |||||
| # | Название (аббревиатура в стиле Боуэрса) | Вершинная фигура | Диаграмма Кокстера и символы Шлефли | Количество клеток по местоположению | Количество элементов | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Поз. 3 (8) | Поз. 2 (24) | Поз. 1 (32) | Поз. 0 (16) | Альт | Клетки | Лица | Края | Вершины | ||||
| Неравномерный | омниснуб тессеракт Плосконосый тессеракт (snet) [17] (Или омниснуб 16-ячеечный ) | 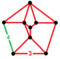 | хт 0,1,2,3 {4,3,3} | (1) (3.3.3.3.4) | (1) (3.3.3.4) | (1) (3.3.3.3) | (1) (3.3.3.3.3) | (4) (3.3.3) | 272 | 944 | 864 | 192 |
16-клеточные усечения
| # | Имя (имя и аббревиатура Bowers) | Вершинная фигура | Диаграмма Кокстера и символы Шлефли | Количество клеток по местоположению | Количество элементов | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Поз. 3 (8) | Поз. 2 (24) | Поз. 1 (32) | Поз. 0 (16) | Альт | Клетки | Лица | Края | Вершины | ||||
| [12] | 16-клеточный гексадекахорон [7] (гекс) | | {3,3,4} | (8) (3.3.3) | 16 | 32 | 24 | 8 | ||||
| [22] | *Ректифицированный 16-элементный (то же, что и 24-элементный ) (ico) |  | = г{3,3,4} | (2) (3.3.3.3) | (4) (3.3.3.3) | 24 | 96 | 96 | 24 | |||
| 17 | Усеченный 16-клеточный усеченный гексадекахорон (текс) |  | т{3,3,4} | (1) (3.3.3.3) | (4) (3.6.6) | 24 | 96 | 120 | 48 | |||
| [23] | *Кантеллированный 16-ячеечный (То же, что и выпрямленный 24-ячеечный ) (rico) |  | = рр{3,3,4} | (1) (3.4.3.4) | (2) (4.4.4) | (2) (3.4.3.4) | 48 | 240 | 288 | 96 | ||
| [15] | Runcinated 16-cell (также runcinated tesseract ) (sidpith) | | т 0,3 {3,3,4} | (1) (4.4.4) | (3) (4.4.4) | (3) (3.4.4) | (1) (3.3.3) | 80 | 208 | 192 | 64 | |
| [16] | Усеченный 16-ячеечный многогранник (также усеченный тессеракт ) (tah) | | 2т{3,3,4} | (2) (4.6.6) | (2) (3.6.6) | 24 | 120 | 192 | 96 | |||
| [24] | *Усеченный 16-ячеечный (То же, что и усеченный 24-ячеечный ) (tico) |  | = тр{3,3,4} | (1) (4.6.6) | (1) (4.4.4) | (2) (4.6.6) | 48 | 240 | 384 | 192 | ||
| 20 | Тессеракт с 16 ячейками призматорогомбированный (прит) |  | т 0,1,3 {3,3,4} | (1) (3.4.4.4) | (1) (4.4.4) | (2) (4.4.6) | (1) (3.6.6) | 80 | 368 | 480 | 192 | |
| [21] | Всеусеченный 16-ячеечный (также всеусеченный тессеракт ) (gidpith) | | т 0,1,2,3 {3,3,4} | (1) (4.6.8) | (1) (4.4.8) | (1) (4.4.6) | (1) (4.6.6) | 80 | 464 | 768 | 384 | |
| [31] | чередующийся усеченный 16-клеточный (то же, что и курносый 24-клеточный ) (сади) |  | ср{3,3,4} | (1) (3.3.3.3.3) | (1) (3.3.3) | (2) (3.3.3.3.3) | (4) (3.3.3) | 144 | 480 | 432 | 96 | |
| Неравномерный | Рунчиц курносый выпрямленный 16-ячеечный пиритосубый тессеракт (pysnet) |  | ст 3 {3,3,4} | (1) (3.4.4.4) | (2) (3.4.4) | (1) (4.4.4) | (1) (3.3.3.3.3) | (2) (3.4.4) | 176 | 656 | 672 | 192 |
- (*) Так же, как ректификация тетраэдра дает октаэдр , ректификация 16-ячеечного дает 24-ячеечный, обычного члена следующего семейства.
Плосконосый 24-ячейник повторяется в этом семействе для полноты. Это чередование усеченного 16-ячейника или усеченного 24-ячейника с группой симметрии половины [(3,3) + ,4]. Усеченные октаэдрические ячейки становятся икосаэдрами. Кубы становятся тетраэдрами, и 96 новых тетраэдров создаются в зазорах от удаленных вершин.
Ф4семья
Это семейство имеет диплоидную икоситетрахорическую симметрию , [7] [3,4,3], порядка 24×48=1152: 48 симметрий октаэдра для каждой из 24 ячеек. Существует 3 малых подгруппы индексов, причем первые две изоморфные пары порождают однородные 4-многогранники, которые также повторяются в других семействах, [3 + ,4,3], [3,4,3 + ] и [3,4,3] + , все порядка 576.
| # | Имя | Вершинная фигура | Диаграмма Кокстера и символы Шлефли | Количество клеток по местоположению | Количество элементов | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Поз. 3 (24) | Поз. 2 (96) | Поз. 1 (96) | Поз. 0 (24) | Клетки | Лица | Края | Вершины | ||||
| 22 | 24-клеточный (То же, что и ректифицированный 16-клеточный ) Икозитетрахорон [7] (ico) |  | {3,4,3} | (6) (3.3.3.3) | 24 | 96 | 96 | 24 | |||
| 23 | выпрямленный 24-ячеечный (то же, что и кантеллированный 16-ячеечный ) Выпрямленный икоситетрахорон (рико) |  | г{3,4,3} | (3) (3.4.3.4) | (2) (4.4.4) | 48 | 240 | 288 | 96 | ||
| 24 | усеченный 24-клеточный (То же, что и усеченный 16-клеточный ) Усеченный икоситетрахорон (тико) |  | т{3,4,3} | (3) (4.6.6) | (1) (4.4.4) | 48 | 240 | 384 | 192 | ||
| 25 | Кантеллированный 24-клеточный Малый ромбический икоситетрахорон (srico) |  | рр{3,4,3} | (2) (3.4.4.4) | (2) (3.4.4) | (1) (3.4.3.4) | 144 | 720 | 864 | 288 | |
| 28 | усеченный 24-клеточный большой ромбический икоситетрахорон (grico) |  | тр{3,4,3} | (2) (4.6.8) | (1) (3.4.4) | (1) (3.8.8) | 144 | 720 | 1152 | 576 | |
| 29 | рунцитусеченный 24-клеточный призматогомбированный икоситетрахорон (прико) |  | т 0,1,3 {3,4,3} | (1) (4.6.6) | (2) (4.4.6) | (1) (3.4.4) | (1) (3.4.4.4) | 240 | 1104 | 1440 | 576 |
| # | Имя | Вершинная фигура | Диаграмма Кокстера и символы Шлефли | Количество клеток по местоположению | Количество элементов | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Поз. 3 (24) | Поз. 2 (96) | Поз. 1 (96) | Поз. 0 (24) | Альт | Клетки | Лица | Края | Вершины | ||||
| 31 | † курносый 24-клеточный курносый дисикозитетрахорон (сади) | | с{3,4,3} | (3) (3.3.3.3.3) | (1) (3.3.3) | (4) (3.3.3) | 144 | 480 | 432 | 96 | ||
| Неравномерный | рунцик курносый 24-клеточный Prissatorhombisnub icositetrachoron (prissi) | 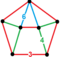 | с 3 {3,4,3} | (1) (3.3.3.3.3) | (2) (3.4.4) | (1) (3.6.6) | (3) Тричашка | 240 | 960 | 1008 | 288 | |
| [25] | Кантик субл 24-клеточный (То же, что и кантеллированный 24-клеточный ) (srico) | 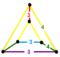 | с 2 {3,4,3} | (2) (3.4.4.4) | (1) (3.4.3.4) | (2) (3.4.4) | 144 | 720 | 864 | 288 | ||
| [29] | runcicantic курносый 24-ячеечный (То же, что и runcitruncated 24-ячеечный ) (prico) |  | с 2,3 {3,4,3} | (1) (4.6.6) | (1) (3.4.4) | (1) (3.4.4.4) | (2) (4.4.6) | 240 | 1104 | 1440 | 576 | |
- (†) Плосконосый 24-ячеечный здесь, несмотря на его общее название, не является аналогом плосконосого куба ; скорее, он получен путем чередования усеченного 24-ячеечного. Его число симметрии составляет всего 576, ( ионная уменьшенная икоситетрахорическая группа, [3 + ,4,3]).
Как и 5-ячеечная, 24-ячеечная является самодвойственной, поэтому следующие три формы имеют вдвое больше симметрий, в результате чего их общее число достигает 2304 ( расширенная икоситетрахорическая симметрия [[3,4,3]]).
| # | Имя | Вершинная фигура | Диаграмма Коксетера и символы Шлефли | Количество клеток по местоположению | Количество элементов | ||||
|---|---|---|---|---|---|---|---|---|---|
| Поз. 3-0 (48) | Поз. 2-1 (192) | Клетки | Лица | Края | Вершины | ||||
| 26 | струйчатый 24-клеточный Малый призматотетраконтоктахорон (спик) |  | т 0,3 {3,4,3} | (2) (3.3.3.3) | (6) (3.4.4) | 240 | 672 | 576 | 144 |
| 27 | укороченный 24-клеточный Тетраконтоктахорон (продолжение) |  | 2т{3,4,3} | (4) (3.8.8) | 48 | 336 | 576 | 288 | |
| 30 | всеусеченный 24-клеточный Большой призматотетраконтоктахорон (гиппический) |  | т 0,1,2,3 {3,4,3} | (2) (4.6.8) | (2) (4.4.6) | 240 | 1392 | 2304 | 1152 |
| # | Имя | Вершинная фигура | Диаграмма Кокстера и символы Шлефли | Количество клеток по местоположению | Количество элементов | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Поз. 3-0 (48) | Поз. 2-1 (192) | Альт | Клетки | Лица | Края | Вершины | ||||
| Неравномерный | omnisnub 24-клеточный Snub tetracontoctachoron (snoc) Snub icositetrachoron (sni) [18] | 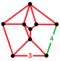 | хт 0,1,2,3 {3,4,3} | (2) (3.3.3.3.4) | (2) (3.3.3.3) | (4) (3.3.3) | 816 | 2832 | 2592 | 576 |
H-образный4семья
Это семейство имеет диплоидную гексакосихорическую симметрию , [7] [5,3,3], порядка 120×120=24×600=14400: 120 для каждого из 120 додекаэдров или 24 для каждого из 600 тетраэдров. Существует одна небольшая подгруппа индексов [5,3,3] + , все порядка 7200.
120-клеточные усечения
| # | Имя (имя и аббревиатура Bowers) | Вершинная фигура | Диаграмма Кокстера и символы Шлефли | Количество клеток по местоположению | Количество элементов | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Поз. 3 (120) | Поз. 2 (720) | Поз. 1 (1200) | Поз. 0 (600) | Альт | Клетки | Лица | Края | Вершины | ||||
| 32 | 120-клеточный (гекатоникосахорон или додекаконтахорон) [7] Гекатоникосахорон (hi) |  | {5,3,3} | (4) (5.5.5) | 120 | 720 | 1200 | 600 | ||||
| 33 | Выпрямленный 120-клеточный Выпрямленный гекатоникосохорон (рахи) |  | г{5,3,3} | (3) (3.5.3.5) | (2) (3.3.3) | 720 | 3120 | 3600 | 1200 | |||
| 36 | усеченный 120-клеточный усеченный гекатоникосохорон (thi) |  | т{5,3,3} | (3) (3.10.10) | (1) (3.3.3) | 720 | 3120 | 4800 | 2400 | |||
| 37 | Кантеллированный 120-клеточный Малый ромбовидный гекатоникосохорон (срахи) |  | рр{5,3,3} | (2) (3.4.5.4) | (2) (3.4.4) | (1) (3.3.3.3) | 1920 | 9120 | 10800 | 3600 | ||
| 38 | 120-клеточный стручковидный (также 600-клеточный стручковидный ) Малый диспризматогексакосигектоникосахорон (sidpixhi) |  | т 0,3 {5,3,3} | (1) (5.5.5) | (3) (4.4.5) | (3) (3.4.4) | (1) (3.3.3) | 2640 | 7440 | 7200 | 2400 | |
| 39 | укороченный 120-клеточный (также укороченный 600-клеточный ) гексакосигектоникосахорон (xhi) |  | 2т{5,3,3} | (2) (5.6.6) | (2) (3.6.6) | 720 | 4320 | 7200 | 3600 | |||
| 42 | усеченный 120-клеточный большой ромбовидный гекатоникосохорон (грахи) |  | тр{5,3,3} | (2) (4.6.10) | (1) (3.4.4) | (1) (3.6.6) | 1920 | 9120 | 14400 | 7200 | ||
| 43 | рунцитоусеченный 120-клеточный призматорогомбированный гексакосихорон (prix) |  | т 0,1,3 {5,3,3} | (1) (3.10.10) | (2) (4.4.10) | (1) (3.4.4) | (1) (3.4.3.4) | 2640 | 13440 | 18000 | 7200 | |
| 46 | всеусеченный 120-клеточный (также всеусеченный 600-клеточный ) Большой диспризматогексакосигектоникосахорон (гидпиксхи) |  | т 0,1,2,3 {5,3,3} | (1) (4.6.10) | (1) (4.4.10) | (1) (4.4.6) | (1) (4.6.6) | 2640 | 17040 | 28800 | 14400 | |
| Неравномерный | omnisnub 120-клеточный Snub hecatonicosachoron (snixhi) [19] (То же, что и omnisnub 600-клеточный ) |  | хт 0,1,2,3 {5,3,3} |  (1) (3.3.3.3.5) |  (1) (3.3.3.5) | (1) (3.3.3.3) | (1) (3.3.3.3.3) | (4) (3.3.3) | 9840 | 35040 | 32400 | 7200 |
600-клеточные усечения
| # | Название (аббревиатура в стиле Боуэрса) | Вершинная фигура | Диаграмма Кокстера и символы Шлефли | Симметрия | Количество клеток по местоположению | Количество элементов | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Поз. 3 (120) | Поз. 2 (720) | Поз. 1 (1200) | Поз. 0 (600) | Клетки | Лица | Края | Вершины | |||||
| 35 | 600-клеточный гексакосихорон [7] (ex) |  | {3,3,5} | [5,3,3] заказ 14400 | (20) (3.3.3) | 600 | 1200 | 720 | 120 | |||
| [47] | 20-уменьшенная 600-ячейка = Большая антипризма (щель) |  | Невитхоффовская конструкция | [[10,2 + ,10]] порядок 400 Индекс 36 | (2) (3.3.3.5) | (12) (3.3.3) | 320 | 720 | 500 | 100 | ||
| [31] | 24-уменьшенный 600-ячейковый = курносый 24-ячейковый (сади) | | Невитхоффовская конструкция | [3 + ,4,3] порядок 576 индекс 25 | (3) (3.3.3.3.3) | (5) (3.3.3) | 144 | 480 | 432 | 96 | ||
| Неравномерный | би-24-уменьшенный 600-клеточный Би-икозитэуменьшенный гексакосихорон (бидекс) |  | Невитхоффовская конструкция | заказ 144 индекс 100 | (6) тди | 48 | 192 | 216 | 72 | |||
| 34 | Выпрямленный 600-клеточный Выпрямленный гексакосихорон (rox) |  | г{3,3,5} | [5,3,3] | (2) (3.3.3.3.3) | (5) (3.3.3.3) | 720 | 3600 | 3600 | 720 | ||
| Неравномерный | 120-уменьшенный выпрямленный 600-клеточный Swirlprismatoуменьшенный выпрямленный гексакосихорон (спидрокс) |  | Невитхоффовская конструкция | заказ 1200 индекс 12 | (2) 3.3.3.5 | (2) 4.4.5 | (5) П4 | 840 | 2640 | 2400 | 600 | |
| 41 | усеченный 600-клеточный усеченный гексакосихорон (текс) |  | т{3,3,5} | [5,3,3] | (1) (3.3.3.3.3) | (5) (3.6.6) | 720 | 3600 | 4320 | 1440 | ||
| 40 | Кантеллированный 600-клеточный малый ромбовидный гексакосихорон (srix) |  | рр{3,3,5} | [5,3,3] | (1) (3.5.3.5) | (2) (4.4.5) | (1) (3.4.3.4) | 1440 | 8640 | 10800 | 3600 | |
| [38] | runcinated 600-клеточный (также runcinated 120-клеточный ) (sidpixhi) | | т 0,3 {3,3,5} | [5,3,3] | (1) (5.5.5) | (3) (4.4.5) | (3) (3.4.4) | (1) (3.3.3) | 2640 | 7440 | 7200 | 2400 |
| [39] | бит-усеченный 600-ячеечный (также бит-усеченный 120-ячеечный ) (xhi) | | 2т{3,3,5} | [5,3,3] | (2) (5.6.6) | (2) (3.6.6) | 720 | 4320 | 7200 | 3600 | ||
| 45 | усеченный 600-клеточный большой ромбовидный гексакосихорон (грикс) |  | тр{3,3,5} | [5,3,3] | (1) (5.6.6) | (1) (4.4.5) | (2) (4.6.6) | 1440 | 8640 | 14400 | 7200 | |
| 44 | рунцитусечённый 600-клеточный призматогомбированный гекатоникосохор (прахи) |  | т 0,1,3 {3,3,5} | [5,3,3] | (1) (3.4.5.4) | (1) (4.4.5) | (2) (4.4.6) | (1) (3.6.6) | 2640 | 13440 | 18000 | 7200 |
| [46] | omniturcated 600-cell (также omniturcated 120-cell ) (gidpixhi) | | т 0,1,2,3 {3,3,5} | [5,3,3] | (1) (4.6.10) | (1) (4.4.10) | (1) (4.4.6) | (1) (4.6.6) | 2640 | 17040 | 28800 | 14400 |
Д4семья
Это семейство полутессерактов , [3 1,1,1 ], не вводит новых однородных 4-многогранников, но стоит повторить эти альтернативные конструкции. Это семейство имеет порядок 12×16=192: 4!/2=12 перестановок четырех осей, в два раза меньше чередующихся, 2 4 =16 для отражения относительно каждой оси. Существует одна небольшая подгруппа индексов, которая порождает однородные 4-многогранники, [3 1,1,1 ] + , порядок 96.
| # | Название (аббревиатура в стиле Боуэрса) | Вершинная фигура | Диаграмма Коксетера == | Количество клеток по местоположению | Количество элементов | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Поз. 0 (8) | Поз. 2 (24) | Поз. 1 (8) | Поз. 3 (8) | Поз. Alt (96) | 3 | 2 | 1 | 0 | ||||
| [12] | полутессеракт демитессеракт (то же, что и 16-ячеечный ) (шестигранник) | | = ч{4,3,3} | (4) (3.3.3) | (4) (3.3.3) | 16 | 32 | 24 | 8 | |||
| [17] | кантический тессеракт (то же, что и усеченный 16-ячеечный ) (thex) | | = ч 2 {4,3,3} | (1) (3.3.3.3) | (2) (3.6.6) | (2) (3.6.6) | 24 | 96 | 120 | 48 | ||
| [11] | рунический тессеракт (то же, что и выпрямленный тессеракт ) (рит) | | = ч 3 {4,3,3} | (1) (3.3.3) | (1) (3.3.3) | (3) (3.4.3.4) | 24 | 88 | 96 | 32 | ||
| [16] | тессеракт ранцикантик (то же, что и битусеченный тессеракт ) (тах) | | = ч 2,3 {4,3,3} | (1) (3.6.6) | (1) (3.6.6) | (2) (4.6.6) | 24 | 96 | 96 | 24 | ||
Когда 3 разветвленных узла ветвления одинаково окольцованы, симметрия может быть увеличена на 6, так как [3[3 1,1,1 ]] = [3,4,3], и, таким образом, эти многогранники повторяются из 24-ячеечного семейства.
| # | Название (аббревиатура в стиле Боуэрса) | Вершинная фигура | Диаграмма Коксетера==  | Количество клеток по местоположению | Количество элементов | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Поз. 0,1,3 (24) | Поз. 2 (24) | Поз. Alt (96) | 3 | 2 | 1 | 0 | ||||
| [22] | выпрямленный 16-элементный (то же, что и 24-элементный ) (ico) |  | === {3 1,1,1 } = р{3,3,4} = {3,4,3} | (6) (3.3.3.3) | 48 | 240 | 288 | 96 | ||
| [23] | Кантеллированный 16-ячеечный (То же, что и выпрямленный 24-ячеечный ) (rico) | | === г{3 1,1,1 } = рр{3,3,4} = г{3,4,3} | (3) (3.4.3.4) | (2) (4.4.4) | 24 | 120 | 192 | 96 | |
| [24] | усеченный 16-ячеечный (то же, что усеченный 24-ячеечный ) (tico) | | === т{3 1,1,1 } = тр{3,3,4} = т{3,4,3} | (3) (4.6.6) | (1) (4.4.4) | 48 | 240 | 384 | 192 | |
| [31] | курносый 24-х ячеечный (сади) | |  === с{3 1,1,1 } = ср{3,3,4} = с{3,4,3} | (3) (3.3.3.3.3) | (1) (3.3.3) | (4) (3.3.3) | 144 | 480 | 432 | 96 |
Здесь снова плосконосый 24-ячейник с группой симметрии [3 1,1,1 ] + на этот раз представляет собой альтернативное усечение усеченного 24-ячейника, создающее 96 новых тетраэдров в позиции удаленных вершин. В отличие от его появления в предыдущих группах как частично плосконосого 4-политопа, только в этой группе симметрии он имеет полную аналогию с плосконосыми Кеплера, т.е. плосконосым кубом и плосконосым додекаэдром .
Великая антипризма
Существует один не-Витхоффов однородный выпуклый 4-мерный многогранник, известный как большая антипризма , состоящий из 20 пятиугольных антипризм, образующих два перпендикулярных кольца, соединенных 300 тетраэдрами . Он примерно аналогичен трехмерным антипризмам , которые состоят из двух параллельных многоугольников , соединенных полосой треугольников . Однако, в отличие от них, большая антипризма не является членом бесконечного семейства однородных многогранников.
Его симметрия — ионная уменьшенная группа Коксетера , [[10,2 + ,10]], порядок 400.
| # | Название (аббревиатура в стиле Боуэрса) | Картина | Вершинная фигура | Диаграмма Кокстера и символы Шлефли | Клетки по типу | Количество элементов | Сеть | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Клетки | Лица | Края | Вершины | ||||||||
| 47 | большая антипризма (щель) |  | 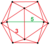| Нет символа | 300 ( 3.3.3 ) | 20 ( 3.3.3.5 ) | 320 | 20 {5} 700 {3} | 500 | 100 |  |
Призматические однородные 4-мерные многогранники
Призматический многогранник — это декартово произведение двух многогранников меньшей размерности; знакомые примеры — 3-мерные призмы , которые являются произведениями многоугольника и отрезка . Призматические однородные 4-мерные многогранники состоят из двух бесконечных семейств:
- Многогранные призмы : произведения отрезка прямой и однородного многогранника. Это семейство бесконечно, поскольку включает призмы, построенные на трехмерных призмах и антипризмах .
- Дуопризмы : произведения двух многоугольников.
Выпуклые многогранные призмы
Наиболее очевидным семейством призматических 4-многогранников являются многогранные призмы, т. е. произведения многогранника с отрезком прямой . Ячейками таких 4-многогранников являются два одинаковых однородных многогранника, лежащих в параллельных гиперплоскостях ( базовые ячейки), и слой призм, соединяющих их ( боковые ячейки). Это семейство включает призмы для 75 непризматических однородных многогранников (из которых 18 выпуклые; один из них, кубическая призма, указан выше как тессеракт ). [ необходима цитата ]
Существует 18 выпуклых многогранных призм, созданных из 5 Платоновых тел и 13 Архимедовых тел, а также для бесконечных семейств трехмерных призм и антипризм . [ необходима ссылка ] Число симметрии многогранной призмы в два раза больше, чем у базового многогранника.
Тетраэдрические призмы: А3× А1
Эта призматическая тетраэдрическая симметрия имеет порядок [3,3,2] 48. Существуют две подгруппы индекса 2, [(3,3) + ,2] и [3,3,2] + , но вторая не порождает однородный 4-многогранник.
| # | Название (аббревиатура в стиле Боуэрса) | Картина | Вершинная фигура | Диаграмма Кокстера и символы Шлефли | Клетки по типу | Количество элементов | Сеть | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Клетки | Лица | Края | Вершины | |||||||||
| 48 | Тетраэдрическая призма (тепе) |  |  | {3,3}×{ } т 0,3 {3,3,2} | 2 3.3.3 | 4 3.4.4 | 6 | 8 {3} 6 {4} | 16 | 8 |  | |
| 49 | Усеченная тетраэдрическая призма (туттип) |  |  | т{3,3}×{ } т 0,1,3 {3,3,2} | 2 3.6.6 | 4 3.4.4 | 4 4.4.6 | 10 | 8 {3} 18 {4} 8 {6} | 48 | 24 |  |
| # | Название (аббревиатура в стиле Боуэрса) | Картина | Вершинная фигура | Диаграмма Кокстера и символы Шлефли | Клетки по типу | Количество элементов | Сеть | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Клетки | Лица | Края | Вершины | |||||||||
| [51] | Выпрямленная тетраэдрическая призма (такая же, как октаэдрическая призма ) (ope) |  |  | г{3,3}×{ } т 1,3 {3,3,2} | 2 3.3.3.3 | 4 3.4.4 | 6 | 16 {3} 12 {4} | 30 | 12 |  | |
| [50] | Конусная тетраэдрическая призма (та же, что и кубооктаэдрическая призма ) (коуп) |  |  | рр{3,3}×{ } т 0,2,3 {3,3,2} | 2 3.4.3.4 | 8 3.4.4 | 6 4.4.4 | 16 | 16 {3} 36 {4} | 60 | 24 |  |
| [54] | Усеченная тетраэдрическая призма (То же, что усеченная октаэдрическая призма ) (tope) |  |  | tr{3,3}×{ } т 0,1,2,3 {3,3,2} | 2 4.6.6 | 8 6.4.4 | 6 4.4.4 | 16 | 48 {4} 16 {6} | 96 | 48 |  |
| [59] | Плосконосая тетраэдрическая призма (такая же, как и икосаэдрическая призма ) (ipe) |  |  | ср{3,3}×{ } | 2 3.3.3.3.3 | 20 3.4.4 | 22 | 40 {3} 30 {4} | 72 | 24 |  | |
| Неравномерный | всеносколотая тетраэдрическая антипризма Пиритоэдрическая икосаэдрическая антипризма (пикап) |  | | 2 3.3.3.3.3 | 8 3.3.3.3 | 6+24 3.3.3 | 40 | 16+96 {3} | 96 | 24 | ||
Октаэдрические призмы: B3× А1
Симметрия этого семейства призматических октаэдров — [4,3,2], порядок 96. Существует 6 подгрупп индекса 2, порядок 48, которые выражены в чередующихся 4-многогранниках ниже. Симметрии — [(4,3) + ,2], [1 + ,4,3,2], [4,3,2 + ], [4,3 + ,2], [4,(3,2) + ] и [4,3,2] + .
| # | Название (аббревиатура в стиле Боуэрса) | Картина | Вершинная фигура | Диаграмма Кокстера и символы Шлефли | Клетки по типу | Количество элементов | Сеть | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Клетки | Лица | Края | Вершины | ||||||||||
| [10] | Кубическая призма (То же, что тессеракт ) (То же, что 4-4 дуопризма ) (тес) |  |  | {4,3}×{ } т 0,3 {4,3,2} | 2 4.4.4 | 6 4.4.4 | 8 | 24 {4} | 32 | 16 |  | ||
| 50 | Кубооктаэдрическая призма (То же, что и усеченная тетраэдрическая призма ) (коуп) | | | г{4,3}×{ } т 1,3 {4,3,2} | 2 3.4.3.4 | 8 3.4.4 | 6 4.4.4 | 16 | 16 {3} 36 {4} | 60 | 24 | | |
| 51 | Октаэдрическая призма (То же, что и выпрямленная тетраэдрическая призма ) (То же, что и треугольная антипризматическая призма ) (ope) | | | {3,4}×{ } т 2,3 {4,3,2} | 2 3.3.3.3 | 8 3.4.4 | 10 | 16 {3} 12 {4} | 30 | 12 | | ||
| 52 | Ромбокубооктаэдрическая призма (сиркопа) |  |  | рр{4,3}×{ } т 0,2,3 {4,3,2} | 2 3.4.4.4 | 8 3.4.4 | 18 4.4.4 | 28 | 16 {3} 84 {4} | 120 | 48 |  | |
| 53 | Усеченная кубическая призма (тиккуп) |  |  | т{4,3}×{ } т 0,1,3 {4,3,2} | 2 3.8.8 | 8 3.4.4 | 6 4.4.8 | 16 | 16 {3} 36 {4} 12 {8} | 96 | 48 |  | |
| 54 | Усеченная октаэдрическая призма (То же, что и усеченная тетраэдрическая призма ) (tope) | | | т{3,4}×{ } т 1,2,3 {4,3,2} | 2 4.6.6 | 6 4.4.4 | 8 4.4.6 | 16 | 48 {4} 16 {6} | 96 | 48 | | |
| 55 | Усеченная кубооктаэдрическая призма (гиркоп) |  |  | tr{4,3}×{ } t 0,1,2,3 {4,3,2} | 2 4.6.8 | 12 4.4.4 | 8 4.4.6 | 6 4.4.8 | 28 | 96 {4} 16 {6} 12 {8} | 192 | 96 |  |
| 56 | Плосконосая кубическая призма (sniccup) |  |  | ср{4,3}×{ } | 2 3.3.3.3.4 | 32 3.4.4 | 6 4.4.4 | 40 | 64 {3} 72 {4} | 144 | 48 |  | |
| [48] | Тетраэдрическая призма (тепе) | | | ч{4,3}×{ } | 2 3.3.3 | 4 3.4.4 | 6 | 8 {3} 6 {4} | 16 | 8 | | ||
| [49] | Усеченная тетраэдрическая призма (туттип) | | | ч 2 {4,3}×{ } | 2 3.3.6 | 4 3.4.4 | 4 4.4.6 | 6 | 8 {3} 6 {4} | 16 | 8 | | |
| [50] | Кубооктаэдрическая призма (коуп) | | | рр{3,3}×{ } | 2 3.4.3.4 | 8 3.4.4 | 6 4.4.4 | 16 | 16 {3} 36 {4} | 60 | 24 | | |
| [52] | Ромбокубооктаэдрическая призма (сиркопа) | | | с 2 {3,4}×{ } | 2 3.4.4.4 | 8 3.4.4 | 18 4.4.4 | 28 | 16 {3} 84 {4} | 120 | 48 | | |
| [54] | Усеченная октаэдрическая призма (топ) | | | тр{3,3}×{ } | 2 4.6.6 | 6 4.4.4 | 8 4.4.6 | 16 | 48 {4} 16 {6} | 96 | 48 | | |
| [59] | Икосаэдрическая призма (ИП) | | | с{3,4}×{ } | 2 3.3.3.3.3 | 20 3.4.4 | 22 | 40 {3} 30 {4} | 72 | 24 | | ||
| [12] | 16-ячеечный (шестигранный) |  | | с{2,4,3} | 2+6+8 3.3.3.3 | 16 | 32 {3} | 24 | 8 |  | |||
| Неравномерный | Омнисноплоская тетраэдрическая антипризма = Пиритоэдрическая икосаэдрическая антипризма (пикап) | | ср{2,3,4} | 2 3.3.3.3.3 | 8 3.3.3.3 | 6+24 3.3.3 | 40 | 16+96 {3} | 96 | 24 | |||
| Неравномерный | Краево-курносый октаэдрический госохорон Пирито-курносый альтерпризма (пысна) |  | ст 3 {2,3,4} | 2 3.4.4.4 | 6 4.4.4 | 8 3.3.3.3 | 24 3.4.4 | 40 | 16+48 {3} 12+12+24+24 {4} | 144 | 48 | ||
| Неравномерный | Кубическая антипризма плосконосая (sniccap) |  | | 2 3.3.3.3.4 | 12+48 3.3.3 | 8 3.3.3.3 | 6 3.3.3.4 | 76 | 16+192 {3} 12 {4} | 192 | 48 | ||
| Неравномерный | Рунический плосконосый кубический хосохорон Усеченная тетраэдрическая альтерпризма (тута) |  |  | с 3 {2,4,3} | 2 3.6.6 | 6 3.3.3 | 8 треугольный купол | 16 | 52 | 60 | 24 |  | |
Икосаэдрические призмы: H3× А1
Эта призматическая икосаэдрическая симметрия имеет порядок [5,3,2] 240. Существуют две подгруппы индекса 2, [(5,3) + ,2] и [5,3,2] + , но вторая не порождает однородный полихор.
| # | Имя (имя и аббревиатура Bowers) | Картина | Вершинная фигура | Диаграмма Кокстера и символы Шлефли | Клетки по типу | Количество элементов | Сеть | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Клетки | Лица | Края | Вершины | ||||||||||
| 57 | Двенадцатигранная призма (легированная) |  |  | {5,3}×{ } т 0,3 {5,3,2} | 2 5.5.5 | 12 4.4.5 | 14 | 30 {4} 24 {5} | 80 | 40 |  | ||
| 58 | Икосододекаэдрическая призма (iddip) | 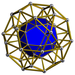 | 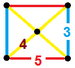 | г{5,3}×{ } т 1,3 {5,3,2} | 2 3.5.3.5 | 20 3.4.4 | 12 4.4.5 | 34 | 40 {3} 60 {4} 24 {5} | 150 | 60 |  | |
| 59 | Икосаэдрическая призма (то же, что и плосконосая тетраэдрическая призма ) (ipe) | | | {3,5}×{ } т 2,3 {5,3,2} | 2 3.3.3.3.3 | 20 3.4.4 | 22 | 40 {3} 30 {4} | 72 | 24 | | ||
| 60 | Усеченная додекаэдрическая призма (tiddip) | 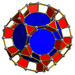 |  | т{5,3}×{ } т 0,1,3 {5,3,2} | 2 3.10.10 | 20 3.4.4 | 12 4.4.10 | 34 | 40 {3} 90 {4} 24 {10} | 240 | 120 |  | |
| 61 | Ромбоикосододекаэдрическая призма (срддип) |  |  | рр{5,3}×{ } т 0,2,3 {5,3,2} | 2 3.4.5.4 | 20 3.4.4 | 30 4.4.4 | 12 4.4.5 | 64 | 40 {3} 180 {4} 24 {5} | 300 | 120 |  |
| 62 | Усеченная икосаэдрическая призма (тип) |  |  | т{3,5}×{ } т 1,2,3 {5,3,2} | 2 5.6.6 | 12 4.4.5 | 20 4.4.6 | 34 | 90 {4} 24 {5} 40 {6} | 240 | 120 |  | |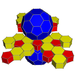
| 63 | Усеченная икосододекаэдрическая призма (сетка) | 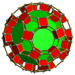 | 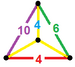 | tr{5,3}×{ } t 0,1,2,3 {5,3,2} | 2 4.6.10 | 30 4.4.4 | 20 4.4.6 | 12 4.4.10 | 64 | 240 {4} 40 {6} 24 {10} | 480 | 240 |  |
| 64 | Плосконосая додекаэдрическая призма (sniddip) |  | 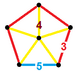 | ср{5,3}×{ } | 2 3.3.3.3.5 | 80 3.4.4 | 12 4.4.5 | 94 | 160 {3} 150 {4} 24 {5} | 360 | 120 |  | |
| Неравномерный | Плосконосая додекаэдрическая антипризма Плосконосая додекаэдрическая антипризма (sniddap) |  | | 2 3.3.3.3.5 | 30+120 3.3.3 | 20 3.3.3.3 | 12 3.3.3.5 | 184 | 20+240 {3} 24 {5} | 220 | 120 | ||
Дуопризмы: [p] × [q]
Второе — бесконечное семейство однородных дуопризм , произведений двух правильных многоугольников . Диаграмма Коксетера-Дынкина дуопризмы — это. Его вершинная фигура — двуклиновидный тетраэдр ,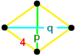
.
Это семейство перекрывается с первым: когда один из двух многоугольников-"факторов" является квадратом, произведение эквивалентно гиперпризме, основание которой является трехмерной призмой. Число симметрии дуопризмы, факторы которой являются p -угольником и q -угольником (a " p,q -дуопризма"), равно 4pq , если p ≠ q ; если факторы оба являются p -угольниками, число симметрии равно 8p2 . Тессеракт также можно считать 4,4-дуопризмой.
Расширенный f-вектор { p }×{ q } равен ( p , p ,1)*( q , q ,1) = ( pq ,2 pq , pq + p + q , p + q ).
- Ячейки: p q -угольные призмы, q p -угольные призмы
- Грани: pq квадратов , pq -угольников , qp -угольников
- Края: 2pq
- Вершины: pq
Не существует единого аналога в четырех измерениях для бесконечного семейства трехмерных антипризм .
Бесконечный набор pq дуопризм -- p q -угольные призмы, q p -угольные призмы:
| Имя | Граф Коксетера | Клетки | Изображения | Сеть |
|---|---|---|---|---|
| 3-3 дуопризма (тридип) | | 3+3 треугольные призмы | |  |
| 3-4 дуопризма (тисдип) | | 3 куба 4 треугольные призмы |   |  |
| 4-4 дуопризма (тес) (то же, что и тессеракт) | | 4+4 кубика |  | |
| 3-5 дуопризма (трапедип) | | 3 пятиугольные призмы 5 треугольных призм |   |  |
| 4-5 дуопризма (сквипидип) | | 4 пятиугольные призмы 5 кубов |   |  |
| 5-5 дуопризма (педип) | | 5+5 пятиугольных призм |  |  |
| 3-6 дуопризма (тридип) |  | 3 шестиугольные призмы 6 треугольных призм |   |  |
| 4-6 дуопризма (шиддип) | | 4 шестиугольные призмы 6 кубов |   |  |
| 5-6 дуопризма (фиддип) | | 5 шестиугольных призм 6 пятиугольных призм |   |  |
| 6-6 дуопризма (хиддип) | | 6+6 шестиугольных призм |  |  |
3-3 | 3-4 | 3-5 | 3-6 |  3-7 |  3-8 |
4-3 | 4-4 | 4-5 | 4-6 |  4-7 |  4-8 |
5-3 | 5-4 | 5-5 | 5-6 |  5-7 |  5-8 |
6-3 | 6-4 | 6-5 | 6-6 |  6-7 |  6-8 |
 7-3 |  7-4 |  7-5 |  7-6 |  7-7 |  7-8 |
 8-3 |  8-4 |  8-5 |  8-6 |  8-7 |  8-8 |
Возможны варианты замены.=дает семейство дуоантипризм , но их, как правило, нельзя сделать однородными. p=q=2 — единственный выпуклый случай, который можно сделать однородным, что дает правильную 16-ячейку. p=5, q=5/3 — единственный невыпуклый случай, который можно сделать однородным, что дает так называемую большую дуоантипризму .дает p-2q-угольную призмантипризму (чередование ребер дуопризмы 2p-4q), но ее нельзя сделать однородной ни в одном случае. [20]
Многоугольные призматические призмы: [p] × [ ] × [ ]
Бесконечное множество однородных призматических призм перекрывается с 4-p дуопризмами: (p≥3) -- p кубы и 4 p -угольные призмы - (Все они такие же, как 4-p дуопризма ) Второй многогранник в серии является более низкой симметрией правильного тессеракта , {4}×{4}.
| Имя | {3}×{4} | {4}×{4} | {5}×{4} | {6}×{4} | {7}×{4} | {8}×{4} | {п}×{4} |
|---|---|---|---|---|---|---|---|
Диаграммы Коксетера | | | | |  |  | |
| Изображение | | | | | | | |
| Клетки | 3 {4}×{}  4 {3}×{} | 4 {4}×{} 4 {4}×{} | 5 {4}×{} 4 {5}×{} | 6 {4}×{} 4 {6}×{} | 7 {4}×{} 4 {7}×{}  | 8 {4}×{} 4 {8}×{} | п {4}×{} 4 {п}×{} |
| Сеть | | | | |  |  |
Многоугольные антипризматические призмы: [p] × [ ] × [ ]
Бесконечные множества однородных антипризматических призм строятся из двух параллельных однородных антипризм ): (p≥2) -- 2 p -угольные антипризмы, соединенные 2 p -угольными призмами и 2p треугольными призмами.
| Имя | с{2,2}×{} | с{2,3}×{} | с{2,4}×{} | с{2,5}×{} | с{2,6}×{} | с{2,7}×{} | с{2,8}×{} | с{2,п}×{} |
|---|---|---|---|---|---|---|---|---|
Диаграмма Коксетера | | | |  |  |  |  | |
| Изображение |  |  |  |  |  |  |  |  |
| Вершинная фигура | | |  |  |  |  |  |  |
| Клетки | 2 с{2,2} (2) {2}×{}= {4} 4 {3}×{} | 2 с{2,3} 2 {3}×{} 6 {3}×{} | 2 с{2,4} 2 {4}×{} 8 {3}×{} | 2 с{2,5} 2 {5}×{} 10 {3}×{} | 2 с{2,6} 2 {6}×{} 12 {3}×{} | 2 с{2,7} 2 {7}×{} 14 {3}×{} | 2 с{2,8} 2 {8}×{} 16 {3}×{} | 2 с{2,п} 2 {п}×{} 2 п {3}×{} |
| Сеть | | |  |  |  |  |  |  |
P -угольная антипризматическая призма имеет 4p треугольник, 4p квадрат и 4 p-угольника. Она имеет 10p ребер и 4p вершин.
Неравномерные чередования
, чередование удаляет половину вершин в двух хиральных наборах вершин из кольцевой формы, однако равномерное решение требует корректировки позиций вершин для одинаковой длины. В четырех измерениях такая корректировка возможна только для 2 чередующихся фигур, тогда как остальные существуют только как неравносторонние чередующиеся фигуры.Коксетер показал только два однородных решения для групп Коксетера ранга 4 со всеми чередующимися кольцами (показано с пустыми круглыми узлами). Первое —, s{2 1,1,1 }, которая представляла собой подгруппу индекса 24 ( симметрия [2,2,2] + , порядок 8) форму полутессеракта ,, h{4,3,3} (симметрия [1 + ,4,3,3] = [3 1,1,1 ], порядок 192). Второе -, s{3 1,1,1 }, которая является подгруппой индекса 6 (симметрия [3 1,1,1 ] + , порядок 96) формы плосконосой 24-клеточной ,, s{3,4,3}, (симметрия [3 + ,4,3], порядок 576).
Другие изменения, такие как, как альтернатива усеченному тессеракту , не может быть сделана однородной, так как решение для равных длин ребер в общем случае переопределено (есть шесть уравнений, но только четыре переменных). Такие неоднородные чередующиеся фигуры могут быть построены как вершинно-транзитивные 4-многогранники путем удаления одного из двух половинных наборов вершин полной окольцованной фигуры, но будут иметь неравные длины ребер. Так же, как и однородные чередования, они будут иметь половину симметрии однородной фигуры, как [4,3,3] + , порядок 192, является симметрией чередующегося всеусеченного тессеракта . [21]
Конструкции Витхоффа с чередованиями производят вершинно-транзитивные фигуры, которые можно сделать равносторонними, но не однородными, поскольку чередующиеся промежутки (вокруг удаленных вершин) создают ячейки, которые не являются регулярными или полурегулярными. Предлагаемое название для таких фигур — чешуйчатые многогранники . [22] Эта категория допускает подмножество тел Джонсона в качестве ячеек, например, треугольный купол .
Каждая конфигурация вершины в теле Джонсона должна существовать в вершинной фигуре. Например, квадратная пирамида имеет две конфигурации вершин: 3.3.4 вокруг основания и 3.3.3.3 на вершине.
Ниже приведены развертки и вершинные фигуры четырех выпуклых равносторонних случаев, а также список ячеек вокруг каждой вершины.
Диаграмма Коксетера | с 3 {2,4,3}, | с 3 {3,4,3}, | Другие | |
|---|---|---|---|---|
| Связь | 24 из 48 вершин ромбокубооктаэдрической призмы | 288 из 576 вершин runcitucated 24-cell | 72 из 120 вершин 600 -ячеечного | 600 из 720 вершин выпрямленного 600-ячеечного |
| Проекция |  |  |  |  Два кольца пирамид |
| Сеть | рунический курносый кубический хосохорон [23] [24] |  рунчик курносый 24-клеточный [25] [26] |  [27] [28] [29] |  [30] [31] |
| Клетки |   |  | | |
| Вершинная фигура | (1) 3.4.3.4: треугольный купол (2) 3.4.6: треугольный купол (1) 3.3.3: тетраэдр (1) 3.6.6: усеченный тетраэдр | (1) 3.4.3.4: треугольный купол (2) 3.4.6: треугольный купол (2) 3.4.4: треугольная призма (1) 3.6.6: усеченный тетраэдр (1) 3.3.3.3.3: икосаэдр | (2) 3.3.3.5: трехмерный икосаэдр (4) 3.5.5: трехмерный икосаэдр | (1) 3.3.3.3: квадратная пирамида (4) 3.3.4: квадратная пирамида (2) 4.4.5: пятиугольная призма (2) 3.3.3.5 пятиугольная антипризма |
Геометрические выводы для 46 непризматических Витхоффовых однородных полихор
46 4-мерных многогранников Витхоффа включают шесть выпуклых правильных 4-мерных многогранников . Остальные сорок могут быть получены из правильных многогранников с помощью геометрических операций, которые сохраняют большую часть или все их симметрии , и, следовательно, могут быть классифицированы по группам симметрии , которые у них есть общие.
 Сводная таблица операций усечения |  Примеры расположения калейдоскопической точки генератора на фундаментальной области. |
Геометрические операции, которые выводят 40 однородных 4-многогранников из правильных 4-многогранников, являются операциями усечения . 4-многогранник может быть усечен по вершинам, ребрам или граням, что приводит к добавлению ячеек, соответствующих этим элементам, как показано в столбцах таблиц ниже.
Диаграмма Коксетера-Дынкина показывает четыре зеркала калейдоскопа Витхоффа как узлы, а ребра между узлами помечены целым числом, показывающим угол между зеркалами ( π / n радиан или 180/ n градусов). Обведенные кружком узлы показывают, какие зеркала активны для каждой формы; зеркало активно относительно вершины, которая не лежит на нем.
| Операция | Символ Шлефли | Симметрия | Диаграмма Коксетера | Описание |
|---|---|---|---|---|
| Родитель | т 0 {п, д, р} | [п,к,р] |  | Исходная правильная форма {p,q,r} |
| Исправление | т 1 {п, д, р} | | Операция усечения применяется до тех пор, пока исходные края не превратятся в точки. | |
| Биректификация (выпрямленное двойное) | т 2 {п, д, р} | | Лица полностью усечены до точек. То же, что и у выпрямленных двойных. | |
| Триректификация ( двойная ) | т 3 {п, д, р} | | Клетки усечены до точек. Регулярный дуальный {r,q,p} | |
| Усечение | т 0,1 {п,q,r} | | Каждая вершина обрезается так, что остается середина каждого исходного ребра. Там, где была вершина, появляется новая ячейка, родительская вершинная фигура . Каждая исходная ячейка также обрезается. | |
| Бит-усечение | т 1,2 {п,д,р} | | Усечение между ректифицированной формой и двойственной ректифицированной формой. | |
| Три-усечение | т 2,3 {п,д,р} | | Усеченный дуальный {r,q,p}. | |
| Кантеллация | т 0,2 {п,q,r} | | Усечение, применяемое к ребрам и вершинам и определяющее прогрессию между обычной и двойственно-выпрямленной формой. | |
| Бикантелляция | т 1,3 {п,д,р} | | Сократённое двойственное {r,q,p}. | |
| Runcination (или расширение ) | т 0,3 {п,q,r} | | Усечение, применяемое к ячейкам, граням и ребрам; определяет прогрессию между правильной формой и двойственной. | |
| Кантитрация | т 0,1,2 {п,q,r} | | Операции отмены и усечения применялись одновременно . | |
| Бикантитрация | т 1,2,3 {п,д,р} | | Усеченное двойственное число {r,q,p}. | |
| Runcitrcation | т 0,1,3 {п,д,р} | | Операции усечения и укорочения применяются одновременно . | |
| Runcicantellation | т 0,2,3 {п,д,р} | | Запустить усеченное двойственное число {r,q,p}. | |
| Омнитрация (runcicantitruncation) | т 0,1,2,3 {п,д,р} | | Применение всех трех операторов. | |
| Половина | ч{2п,3,q} | [1 + ,2p,3,q] =[(3,p,3),q] | | Чередование, то же самое, что и  |
| Кантик | ч 2 {2п,3,д} | | То же самое, что и | |
| Рунчич | ч 3 {2п,3,д} | | То же самое, что и | |
| Runcicantic | ч 2,3 {2п,3,q} | | То же самое, что и | |
| Четверть | д{2п,3,2д} | [1 + ,2p,3,2q,1 + ] | | То же самое, что и    |
| Пренебрежительное отношение | с{п,2q,r} | [п + ,2q,r] | | Альтернативное усечение |
| Кантик пренебрежение | с 2 {п,2q,r} | | Кантеллированное чередующееся усечение | |
| Рунчич пренебрежение | с 3 {п,2q,r} | | Runcinated чередующееся усечение | |
| Runcicantic пренебрежительное отношение | с 2,3 {п,2q,r} | | Ранцикантеллированное чередующееся усечение | |
| Снуб выпрямленный | ср{п,д,2р} | [(п,q) + ,2r] | | Альтернативное усеченное ректификация |
| ht 0,3 {2p,q,2r} | [(2п,д,2р,2 + )] | | Попеременный бег | |
| Бишнуб | 2с{2п,д,2р} | [2p,q + ,2r] | | Альтернативное битоусечение |
| Omnisnub | ht 0,1,2,3 {п,д,р} | [п,к,р] + | | Попеременное омни-усечение |
См. также выпуклые однородные соты , некоторые из которых иллюстрируют эти операции применительно к правильным кубическим сотам .
Если два многогранника являются дуальными друг другу (например, тессеракт и 16-ячеечный, или 120-ячеечный и 600-ячеечный), то bitruncating , runcinating или omnitruncating либо производят ту же самую фигуру, что и та же операция для другого. Таким образом, если в таблице появляется только причастие, следует понимать, что оно применяется к любому из родителей.
Резюме построений по расширенной симметрии
46 однородных полихор, построенных из симметрии A 4 , B 4 , F 4 , H 4 , даны в этой таблице по их полной расширенной симметрии и диаграммам Коксетера. Симметрия D 4 также включена, хотя она создает только дубликаты. Чередования сгруппированы по их хиральной симметрии. Даны все чередования, хотя курносая 24-ячеечная , с ее 3 конструкциями из разных семейств, является единственной, которая является однородной. Числа в скобках либо повторяются, либо неравномерны. Диаграммы Коксетера даны с нижними индексами от 1 до 46. Включено дуопризматическое семейство 3-3 и 4-4, второе по его отношению к семейству B 4 .
| Группа Коксетера | Расширенная симметрия | Полихора | Хиральная расширенная симметрия | Чередование сот | ||
|---|---|---|---|---|---|---|
| [3,3,3] | [3,3,3] (заказ 120) | 6 | (1) |(2) |(3)(4) |(7) |(8) | |||
| [2 + [3,3,3]] (заказ 240) | 3 | (5) |(6) |(9) | [2 + [3,3,3]] + (порядок 120) | (1) | (−) | |
| [3,3 1,1 ] | [3,3 1,1 ] (приказ 192) | 0 | (никто) | |||
[1[3,3 1,1 ]]=[4,3,3] =(приказ 384) | (4) | (12) |(17) |(11) |(16) | ||||
| [3[3 1,1,1 ]]=[3,4,3]= (приказ 1152) | (3) | (22) |(23) |(24) | [3[3,3 1,1 ]] + =[3,4,3] + (порядок 576) | (1) | (31) (=)(−) | |
| [4,3,3] | [3[1 + ,4,3,3]]=[3,4,3]= (приказ 1152) | (3) | (22) |(23) |(24) | |||
| [4,3,3] (приказ 384) | 12 | (10) |(11) |(12) |(13) |(14)(15) |(16) |(17) |(18) |(19)(20) |(21) | [1 + ,4,3,3] + (порядок 96) | (2) | (12) (=)(31)(−) | |
| [4,3,3] + (порядок 192) | (1) | (−) | ||||
| [3,4,3] | [3,4,3] (приказ 1152) | 6 | (22) |(23) |(24)(25) |(28) |(29) | [2 + [3 + ,4,3 + ]] (порядок 576) | 1 | (31) |
| [2 + [3,4,3]] (приказ 2304) | 3 | (26) |(27) |(30) | [2 + [3,4,3]] + (порядок 1152) | (1) | (−) | |
| [5,3,3] | [5,3,3] (заказ 14400) | 15 | (32) |(33) |(34) |(35) |(36)(37) |(38) |(39) |(40) |(41)(42) |(43) |(44) |(45) |(46) | [5,3,3] + (порядок 7200) | (1) | (−) |
| [3,2,3] | [3,2,3] (заказ 36) | 0 | (никто) | [3,2,3] + (порядок 18) | 0 | (никто) |
| [2 + [3,2,3]] (приказ 72) | 0 | | [2 + [3,2,3]] + (порядок 36) | 0 | (никто) | |
| [[3],2,3]=[6,2,3]= (приказ 72) | 1 | | [1[3,2,3]]=[[3],2,3] + =[6,2,3] + (порядок 36) | (1) | | |
| [(2 + ,4)[3,2,3]]=[2 + [6,2,6]]= (приказ 288) | 1 | | [(2 + ,4)[3,2,3]] + =[2 + [6,2,6]] + (порядок 144) | (1) | | |
| [4,2,4] | [4,2,4] (приказ 64) | 0 | (никто) | [4,2,4] + (порядок 32) | 0 | (никто) |
| [2 + [4,2,4]] (приказ 128) | 0 | (никто) | [2 + [(4,2 + ,4,2 + )]] (порядок 64) | 0 | (никто) | |
| [(3,3)[4,2*,4]]=[4,3,3]= (приказ 384) | (1) | (10) | [(3,3)[4,2*,4]] + =[4,3,3] + (порядок 192) | (1) | (12) | |
| [[4],2,4]=[8,2,4]= (приказ 128) | (1) | | [1[4,2,4]]=[[4],2,4] + =[8,2,4] + (порядок 64) | (1) | | |
| [(2 + ,4)[4,2,4]]=[2 + [8,2,8]]= (приказ 512) | (1) | | [(2 + ,4)[4,2,4]] + =[2 + [8,2,8]] + (порядок 256) | (1) | | |
Равномерная звездчатая полихора
Помимо вышеупомянутых бесконечных семейств дуопризм и антипризм, которые имеют бесконечно много невыпуклых членов, было открыто много однородных звездчатых полихор. В 1852 году Людвиг Шлефли открыл четыре правильных звездчатых полихора: {5,3,5/2}, {5/2,3,5}, {3,3,5/2} и {5/2,3,3}. В 1883 году Эдмунд Гесс нашел остальные шесть: {3,5,5/2}, {5/2,5,3}, {5,5/2,5}, {5/2,5,5/2}, {5,5/2,3} и {3,5/2,5}. Норман Джонсон описал три однородных антипризменных звездчатых полихора в своей докторской диссертации 1966 года: они основаны на трех дитригональных многогранниках, разделяющих ребра и вершины правильного додекаэдра. С тех пор было обнаружено еще много других исследователей, включая Джонатана Бауэрса и Джорджа Ольшевского, что в настоящее время составляет 2127 известных однородных звездных полихор (не считая бесконечного множества дуопризм, основанных на звездных полигонах). В настоящее время нет доказательств полноты этого множества.
Смотрите также
- Конечные правильные косые многогранники 4-мерного пространства
- Выпуклые однородные соты - связанные бесконечные 4-мерные многогранники в евклидовом 3-мерном пространстве.
- Выпуклые однородные соты в гиперболическом пространстве - связанные бесконечные 4-мерные многогранники в гиперболическом 3-мерном пространстве.
- Паракомпактные однородные соты
Ссылки
- ^ NW Johnson : Геометрии и преобразования , (2018) ISBN 978-1-107-10340-5 Глава 11: Конечные группы симметрии , 11.1 Многогранники и соты , стр.224
- ^ Т. Госсет : О правильных и полуправильных фигурах в пространстве n измерений , Вестник математики, Макмиллан, 1900
- ^ "Архивная копия" (PDF) . Архивировано из оригинала (PDF) 2009-12-29 . Получено 2010-08-13 .
{{cite web}}: CS1 maint: архивная копия как заголовок ( ссылка ) - ^ Элте (1912)
- ^ Однородные многогранники в четырех измерениях 6 декабря 1998 г. старейший архив
- ^ Универсальная книга математики: от абракадабры до парадоксов Зенона Дэвида Дарлинга, (2004) ASIN: B00SB4TU58
- ^ abcdefghijk Джонсон (2015), Глава 11, раздел 11.5 Сферические группы Коксетера, 11.5.5 Полные полихорические группы
- ^ Однородные многогранники в четырех измерениях, Джордж Ольшевский.
- ^ Мёллер, Марко (2004). Viersizede Archimedische Polytope (PDF) (Докторская диссертация) (на немецком языке). Университет Гамбурга.
- ^ Конвей (2008)
- ^ Многомерный глоссарий, Джордж Ольшевский
- ^ https://www.mit.edu/~hlb/Associahedron/program.pdf Семинар по выпуклым и абстрактным многогранникам (2005), Н.Джонсон — «Однородная многогранница» аннотация
- ^ ab "Uniform Polychora". www.polytope.net . Получено 20 февраля 2020 г. .
- ^ "Однородный многогранник". Polytope Wiki . 6 ноября 2023 г. Получено 11 ноября 2023 г.
- ^ Коксетер, Правильные многогранники, 7.7 Критерий Шлефли ур. 7.78, стр.135
- ^ "С3с3с3с".
- ^ "S3s3s4s".
- ^ "S3s4s3s".
- ^ "S3s3s5s".
- ^ sns2s2mx, Ричард Клитцинг
- ^ HSM Coxeter, Regular and Semi-Regular Polytopes II, [Math. Zeit. 188 (1985) стр. 582-588 2.7 Четырехмерные аналоги плосконосого куба
- ^ "Многогранник-дерево".
- ^ "тута".
- ^ Категория S1: Простые чешуевидные tutcup
- ^ "Присси".
- ^ Категория S3: Особые чешуекрылые
- ^ "bidex". bendwavy.org . Получено 11 ноября 2023 г. .
- ^ Категория S3: Специальные чешуевидные двудольные
- ^ Би-икозитол уменьшил 600 ячеек
- ^ "spidrox". bendwavy.org . Получено 11 ноября 2023 г. .
- ^ Категория S4: Чешуйчатые спиральные призмы spidrox
- А. Буль Стотт : Геометрический вывод полуправильных многогранников из правильных многогранников и пространственного заполнения , Verhandelingen из Koninklijke academy van Wetenschappen, единица ширины Амстердам, Eerste Sectie 11,1, Амстердам, 1910 г.
- B. Grünbaum Convex Polytopes , Нью-Йорк; Лондон: Springer, c2003. ISBN 0-387-00424-6 . Второе издание подготовили Фолькер Кайбель, Виктор Клее и Гюнтер М. Циглер.
- Эльте, EL (1912), Полуправильные многогранники гиперпространств , Гронинген: Гронингенский университет, ISBN 1-4181-7968-XПолуправильные многогранники гиперпространств. Полуправильные многогранники гиперпространств.
- HSM Коксетер :
- HSM Coxeter, MS Longuet-Higgins и JCP Miller: Однородные многогранники , Philosophical Transactions of the Royal Society of London, London, 1954
- HSM Coxeter, Правильные многогранники , 3-е издание, Довер, Нью-Йорк, 1973
- Калейдоскопы: избранные труды Х. С. М. Коксетера , под редакцией Ф. Артура Шерка, Питера МакМаллена, Энтони К. Томпсона, Азии Айвик Вайс, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6
- (Документ 22) HSM Coxeter, Правильные и полуправильные многогранники I , [Math. Zeit. 46 (1940) 380-407, MR 2,10]
- (Документ 23) HSM Coxeter, Правильные и полуправильные многогранники II , [Math. Zeit. 188 (1985) 559-591]
- (Документ 24) HSM Coxeter, Правильные и полуправильные многогранники III , [Math. Zeit. 200 (1988) 3-45]
- HSM Coxeter и WOJ Moser. Генераторы и отношения для дискретных групп , 4-е изд., Springer-Verlag. Нью-Йорк. 1980 стр. 92, стр. 122.
- Джон Х. Конвей , Хайди Берджил, Хаим Гудман-Штраус , Симметрии вещей 2008, ISBN 978-1-56881-220-5 (глава 26)
- Джон Х. Конвей и М. Дж. Т. Гай : Четырехмерные архимедовы многогранники , Труды коллоквиума по выпуклости в Копенгагене, стр. 38 и 39, 1965 г.
- NW Johnson : Теория однородных многогранников и сот , докторская диссертация, Университет Торонто, 1966 г.
- NW Johnson: Геометрии и преобразования , (2015) Глава 11: Конечные группы симметрии
- Ричард Клитцинг, Снубы, чередующиеся огранки и диаграммы Стотта-Коксетера-Дынкина , Симметрия: Культура и наука, т. 21, № 4, 329-344, (2010) [1]
- Шуте, Питер Хендрик (1911), «Аналитическая обработка многогранников, регулярно полученных из правильных многогранников», Verhandelingen der Koninklijke Akademie van Wetenschappen te Amsterdam , 11 (3): 87 стр.Гуглбук, 370-381
Внешние ссылки
- Выпуклые однородные 4-мерные многогранники
- Однородные, выпуклые многогранники в четырех измерениях, Марко Мёллер (на немецком) . Включает альтернативные названия для этих фигур, в том числе от Джонатана Бауэрса, Джорджа Ольшевского и Нормана Джонсона.
- Правильные и полуправильные выпуклые многогранники краткий исторический обзор
- Java3D-апплеты с исходниками
- Невыпуклые однородные 4-многогранники
- Равномерная полихора Джонатана Бауэрса
- Stella4D Stella (программное обеспечение) создает интерактивные виды известных однородных полихор, включая 64 выпуклые формы и бесконечные призматические семейства.
- Клитцинг, Ричард. «4D однородные многогранники».
- 4D-многогранники и их дуальные многогранники группы Коксетера W(A4), представленные кватернионами Международный журнал геометрических методов в современной физике, т. 9, № 4 (2012) Мехмет Коджа, Назифе Оздеш Коджа, Мудхахир Аль-Аджми (2012) [2]
