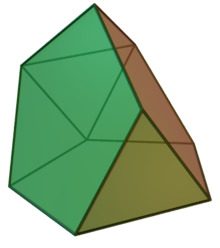
Трехмерный икосаэдр

Трехмерный икосаэдр
Трехмерный икосаэдр
Тип	Джонсон ; Дж 62 – Дж 63 – Дж 64
Лица	5 треугольников; 3 пятиугольника
Края	15
Вершины	9
Конфигурация вершины	2 × 3 × ( 3 × 5 2 ) + 3 × ( 3 3 × 5 ) {\displaystyle 2\times 3\times (3\times 5^{2})+3\times (3^{3}\times 5)}
Группа симметрии	С 3 в {\displaystyle C_{3\mathrm {v} }}
Характеристики	выпуклый , ; несоставной
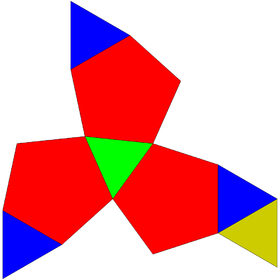
Сеть

63-й Джонсон солидный

В геометрии трехмерный икосаэдр — это многогранник Джонсона , который получается путем удаления трех пятиугольных пирамид из правильного икосаэдра .

Строительство

Триуменьшённый икосаэдр может быть построен путём удаления трёх правильных пятиугольных пирамид из правильного икосаэдра . ^[1] Последствие такого построения оставляет пять равносторонних треугольников и три правильных пятиугольника . ^[2] Поскольку все его грани являются правильными многоугольниками , а полученный многогранник остаётся выпуклым , триуменьшённый икосаэдр является телом Джонсона , и он нумеруется как шестьдесят третье тело Джонсона . ^[3] Эта конструкция похожа на другие тела Джонсона, такие как гироудлинённая пятиугольная пирамида и метабиуменьшённый икосаэдр . ^[1] $J_{63}$

Трёхмерный икосаэдр является несоставным многогранником , то есть это выпуклый многогранник, который не может быть разделён плоскостью на два или более правильных многогранника . ^[4]

Характеристики

Площадь поверхности триадминизированного икосаэдра равна сумме площадей всех многоугольных граней: пяти равносторонних треугольников и трех правильных пятиугольников. Ее объем можно определить, вычитая объем правильного икосаэдра из объема трех пятиугольных пирамид. Учитывая, что — длина ребра триадминизированного икосаэдра, они равны: ^[2] $А$ $V$ $а$ ${\begin{aligned}A&={\frac {5{\sqrt {3}}+3{\sqrt {5\left(5+2{\sqrt {5}}\right)}}}{4}}a^{2}&\approx 7.3265a^{2},\\V&={\frac {15+7{\sqrt {5}}}{24}}a^{3}&\approx 1.2772a^{3}.\end{aligned}}$

Смотрите также

Плосконосый 24-ячейник , 4-мерный многогранник , вершинная фигура которого представляет собой трехмерный икосаэдр

Ссылки

^ аб Гайлюнас, Пол (2001), «Многогранная дорога» (PDF) , в Сарханги, Реза; Яблан, Славик (ред.), Мосты: математические связи в искусстве, музыке и науке , Конференция Бриджеса, стр. 115–122 ..
^ ab Берман, Мартин (1971), «Выпуклые многогранники с правильными гранями», Журнал Института Франклина , 291 (5): 329–352 , doi :10.1016/0016-0032(71)90071-8, MR 0290245 .
^ Фрэнсис, Даррил (август 2013 г.), «Твердые тела Джонсона и их аббревиатуры», Word Ways , 46 (3): 177
^ Тимофеенко, А.В. (2009), «Выпуклые многогранники с паркетными гранями» (PDF) , Docklady Mathematics , 80 (2): 720– 723, doi :10.1134/S1064562409050238.

Внешние ссылки

Вайсштейн, Эрик В. , «Трехмерный икосаэдр» («Твердое тело Джонсона») на MathWorld .

[gailiunas-1] аб Гайлюнас, Пол (2001), «Многогранная дорога» (PDF) , в Сарханги, Реза; Яблан, Славик (ред.), Мосты: математические связи в искусстве, музыке и науке , Конференция Бриджеса, стр. 115–122 ..

[berman-2] Берман, Мартин (1971), «Выпуклые многогранники с правильными гранями», Журнал Института Франклина , 291 (5): 329–352 , doi :10.1016/0016-0032(71)90071-8, MR 0290245 .

[francis-3] Фрэнсис, Даррил (август 2013 г.), «Твердые тела Джонсона и их аббревиатуры», Word Ways , 46 (3): 177

[timofeenko-2009-4] Тимофеенко, А.В. (2009), «Выпуклые многогранники с паркетными гранями» (PDF) , Docklady Mathematics , 80 (2): 720– 723, doi :10.1134/S1064562409050238.

Трехмерный икосаэдр

Тип	Джонсон $Дж 62 - Дж 63 - Дж 64$
Лица	5 треугольников 3 пятиугольника
Края	15
Вершины	9
Конфигурация вершины	$2\times 3\times (3\times 5^{2})+3\times (3^{3}\times 5)$
Группа симметрии	$C_{3\mathrm {v} }$
Характеристики	выпуклый , несоставной
Сеть