Тессеракт с кантеллированными углами
 тессеракт        | 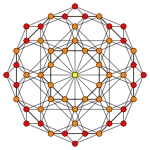 Тессеракт с кантеллированными углами        |  Кантеллированный 16-ячеечный ( ректифицированный 24-ячеечный )        |
 16-ячеечный        |  Усеченный тессеракт        | 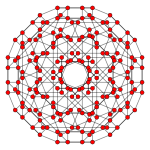 Усеченный 16-ячеечный ( Усеченный 24-ячеечный )        |
| Ортогональные проекции в плоскости Коксетера A 4 | ||
|---|---|---|
В четырехмерной геометрии тессеракт с кантелляцией — это выпуклый однородный 4-мерный многогранник , являющийся кантелляцией (усечением 2-го порядка) правильного тессеракта .
Существует четыре степени кантелляции тессеракта, включая перестановки и усечения. Две из них также получены из 24-клеточного семейства.
Тессеракт с кантеллированными углами
| Тессеракт с кантеллированными углами | ||
|---|---|---|
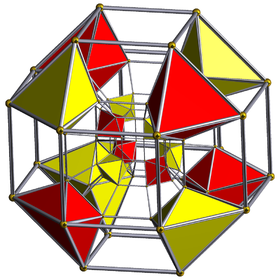 Диаграмма Шлегеля , в центре которой изображены ромбокубооктаэдрические октаэдрические ячейки | ||
| Тип | Однородный 4-многогранник | |
| Символ Шлефли | рр{4,3,3} | |
| Диаграмма Коксетера |        | |
| Клетки | 56 | 8 3.4.4.4  16 3.3.3.3  32 3.4.4  |
| Лица | 248 | 128 {3} 120 {4} |
| Края | 288 | |
| Вершины | 96 | |
| Вершинная фигура |  Квадратный клин | |
| Группа симметрии | B 4 , [3,3,4], порядок 384 | |
| Характеристики | выпуклый | |
| Единый индекс | 13 14 15 | |

Скобовидный тессеракт , бискобовидный 16-ячейниковый или малый ромбический тессеракт представляет собой выпуклый однородный 4 -мерный многогранник , ограниченный 56 ячейками : 8 малыми ромбокубооктаэдрами , 16 октаэдрами и 32 треугольными призмами .
Строительство
В процессе кантеллирования 2-грани многогранника эффективно сжимаются. Ромбокубооктаэдр можно назвать кантеллированным кубом, поскольку если его шесть граней сжать в соответствующих плоскостях, каждая вершина разделится на три вершины треугольников ромбокубооктаэдра, а каждое ребро разделится на два противоположных ребра двенадцати неосевых квадратов ромбокубооктаэдра.
Когда тот же процесс применяется к тессеракту, каждый из восьми кубов становится ромбокубооктаэдром описанным способом. Кроме того, однако, поскольку ребро каждого куба ранее было общим с двумя другими кубами, разделяющие ребра образуют три параллельных ребра треугольной призмы — 32 треугольные призмы, поскольку было 32 ребра. Кроме того, поскольку каждая вершина ранее была общей с тремя другими кубами, вершина разделилась бы на 12, а не на три новых вершины. Однако, поскольку некоторые из сжатых граней продолжают быть общими, определенные пары из этих 12 потенциальных вершин идентичны друг другу, и поэтому из каждой исходной вершины создается только 6 новых вершин (отсюда 96 вершин усеченного тессеракта по сравнению с 16 вершинами тессеракта). Эти шесть новых вершин образуют вершины октаэдра — 16 октаэдров, поскольку тессеракт имел 16 вершин.
Декартовы координаты
Декартовы координаты вершин конического тессеракта с длиной ребра 2 задаются всеми перестановками:
Структура
8 малых ромбокубооктаэдрических ячеек соединены друг с другом через их осевые квадратные грани. Их неосевые квадратные грани, которые соответствуют ребрам куба, соединены с треугольными призмами. Треугольные грани малых ромбокубооктаэдров и треугольных призм соединены с 16 октаэдрами.
Его структуру можно представить с помощью самого тессеракта: ромбокубооктаэдры аналогичны ячейкам тессеракта, треугольные призмы аналогичны ребрам тессеракта, а октаэдры аналогичны вершинам тессеракта.
Изображения
| самолет Коксетера | Б 4 | Б 3 / Д 4 / А 2 | Б 2 / Д 3 |
|---|---|---|---|
| График |  |  |  |
| Диэдральная симметрия | [8] | [6] | [4] |
| самолет Коксетера | Ф 4 | А 3 | |
| График |  |  | |
| Диэдральная симметрия | [12/3] | [4] |
 Каркас | 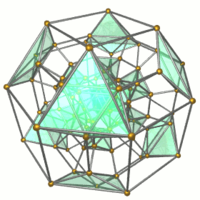 Показаны 16 октаэдров . |  Показаны 32 треугольные призмы . |
Прогнозы
Ниже представлена схема ячеек конусообразного тессеракта при параллельной проекции в трехмерное пространство, сначала малый ромбокубооктаэдр:
- Проекционная оболочка представляет собой усеченный куб .
- Ближайшие и самые дальние от точки зрения 4D малые ромбокубооктаэдрические ячейки проецируются на объем той же формы, вписанный в оболочку проекции.
- Осевые квадраты этого центрального малого ромбокубооктаэдра касаются центров 6 восьмиугольников оболочки. Восьмиугольники являются изображением других 6 малых ромбокубооктаэдрических ячеек.
- 12 клиновидных объемов, соединяющих неосевые квадратные грани центрального малого ромбокубооктаэдра с соседними восьмиугольниками, являются изображениями 24 треугольных призм.
- Оставшиеся 8 треугольных призм проецируются на треугольные грани оболочки.
- Между треугольными гранями оболочки и треугольными гранями центрального малого ромбокубооктаэдра расположены 8 октаэдрических объемов, которые являются изображениями 16 октаэдрических ячеек.
Такое расположение ячеек в проекции аналогично расположению граней в проекции усеченного куба в 2 измерениях. Следовательно, тессеракт с кантеллой можно рассматривать как аналог усеченного куба в 4 измерениях. (Это не единственный возможный аналог; другим близким кандидатом является усеченный тессеракт .)
Другим однородным 4-мерным многогранником с похожей компоновкой ячеек является усеченный 16-мерный многогранник .
Усеченный тессеракт
| Усеченный тессеракт | ||
 Диаграмма Шлегеля , центрированная на ячейке усеченного кубооктаэдра со скрытыми восьмиугольными гранями. | ||
| Тип | Однородный 4-многогранник | |
| Символ Шлефли | тр{4,3,3} | |
| Диаграммы Коксетера |             | |
| Клетки | 56 | 8 4.6.8  16 3.6.6  32 3.4.4  |
| Лица | 248 | 64 {3} 96 {4} 64 {6} 24 {8} |
| Края | 384 | |
| Вершины | 192 | |
| Вершинная фигура | 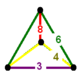 клиновидная кость | |
| Группа симметрии | B 4 , [3,3,4], порядок 384 | |
| Характеристики | выпуклый | |
| Единый индекс | 17 18 19 | |

В геометрии усеченный тессеракт или большой ромбический тессеракт представляет собой однородный 4 -мерный многогранник , ограниченный 56 ячейками : 8 усеченными кубооктаэдрами , 16 усеченными тетраэдрами и 32 треугольными призмами .
Строительство
Кантитрункированный тессеракт строится путем кантитрункации тессеракта . Кантитрункацию часто считают ректификацией, за которой следует усечение. Однако результатом этого построения будет многогранник, структура которого будет очень похожа на структуру, полученную путем кантитрункации, но не все его грани будут однородными.
В качестве альтернативы, однородный усеченный тессеракт может быть построен путем размещения 8 однородных усеченных кубооктаэдров в гиперплоскостях ячеек тессеракта, смещенных вдоль осей координат таким образом, чтобы их восьмиугольные грани совпадали. Для длины ребра 2 эта конструкция дает декартовы координаты его вершин как все перестановки:
Структура
8 усеченных кубооктаэдров соединены друг с другом посредством своих восьмиугольных граней, в расположении, соответствующем 8 кубическим ячейкам тессеракта. Они соединены с 16 усеченными тетраэдрами посредством своих шестиугольных граней, а их квадратные грани соединены с квадратными гранями 32 треугольных призм. Треугольные грани треугольных призм соединены с усеченными тетраэдрами.
Усеченные тетраэдры соответствуют вершинам тессеракта, а треугольные призмы — ребрам тессеракта.
Изображения
| самолет Коксетера | Б 4 | Б 3 / Д 4 / А 2 | Б 2 / Д 3 |
|---|---|---|---|
| График |  |  |  |
| Диэдральная симметрия | [8] | [6] | [4] |
| самолет Коксетера | Ф 4 | А 3 | |
| График |  |  | |
| Диэдральная симметрия | [12/3] | [4] |
 Стереографическая проекция усеченного тессеракта в виде мозаики на 3-сфере с ее 64 синими треугольниками, 96 зелеными квадратами и 64 красными шестиугольными гранями (восьмиугольные грани не изображены). |
Прогнозы
В первой параллельной проекции усеченного кубооктаэдра в трех измерениях ячейки усеченного тессеракта располагаются следующим образом:
- Проекционная оболочка представляет собой неоднородный усеченный куб с более длинными ребрами между восьмиугольниками и более короткими ребрами в 8 треугольниках.
- Неправильные восьмиугольные грани оболочки соответствуют изображениям 6 из 8 усеченных кубооктаэдрических ячеек.
- Две другие усеченные кубооктаэдрические ячейки проецируются на усеченный кубооктаэдр, вписанный в проекционную оболочку. Восьмиугольные грани касаются неправильных восьмиугольников оболочки.
- В пространствах, соответствующих ребрам куба, расположены 12 объемов в форме неправильных треугольных призм. Это изображения, по одному на пару, 24 ячеек треугольной призмы.
- Оставшиеся 8 треугольных призм проецируются на треугольные грани проекционной оболочки.
- Оставшиеся 8 ячеек, соответствующие углам куба, являются изображениями 16 усеченных тетраэдров, по паре на каждую ячейку.
Такое расположение ячеек в проекции похоже на расположение ячеек в конусообразном тессеракте.
Альтернативные названия
- Усеченный тессеракт ( Норман У. Джонсон )
- Усеченный 4-куб
- Канти-усеченный 8-клеточный
- Кантиусечённый октахорон
- Большой призматотессерактигексадекахорон (Георгий Ольшевский)
- Грит (Джонатан Бауэрс: для большого ромбовидного тессеракта)
- 012-ambo тессеракт ( Джон Конвей )
Связанные однородные многогранники
| Многогранники симметрии B4 | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Имя | тессеракт | выпрямленный тессеракт | усеченный тессеракт | тессеракт с конусом | рунический тессеракт | битусеченный тессеракт | усеченный тессеракт | бежатьусеченныйтессеракт | омниусеченный тессеракт | ||
Диаграмма Коксетера |        |        =      |        |        |        |        =      |        |        |        | ||
Символ Шлефли | {4,3,3} | т 1 {4,3,3} р{4,3,3} | т 0,1 {4,3,3} т{4,3,3} | т 0,2 {4,3,3} рр{4,3,3} | т 0,3 {4,3,3} | т 1,2 {4,3,3} 2т{4,3,3} | т 0,1,2 {4,3,3} тр{4,3,3} | т 0,1,3 {4,3,3} | т 0,1,2,3 {4,3,3} | ||
Диаграмма Шлегеля |  |  |  |  |  |  |  |  |  | ||
| Б 4 |  |  |  |  |  |  |  |  |  | ||
| Имя | 16-ячеечный | выпрямленный 16-элементный | усеченный 16-клеточный | кантеллированный 16-ячеечный | 16 -клеточный | усеченный 16-ячеечный | кантит-усеченный 16-клеточный | runcitucated 16-ячеечный | усеченный 16-ячеечный | ||
Диаграмма Коксетера |        =      |        =      |        =      |        =      |        |        =      |        =      |        |        | ||
Символ Шлефли | {3,3,4} | т 1 {3,3,4} р{3,3,4} | т 0,1 {3,3,4} т{3,3,4} | т 0,2 {3,3,4} рр{3,3,4} | т 0,3 {3,3,4} | т 1,2 {3,3,4} 2т{3,3,4} | т 0,1,2 {3,3,4} тр{3,3,4} | т 0,1,3 {3,3,4} | т 0,1,2,3 {3,3,4} | ||
Диаграмма Шлегеля |  |  |  |  |  |  |  |  |  | ||
| Б 4 |  |  |  |  |  |  |  |  |  | ||
Он является вторым в серии усеченных гиперкубов:
  |   |   |   |   |   |
| Усеченный кубооктаэдр | Усеченный тессеракт | Усеченный 5-куб | Усеченный 6-куб | Усеченный 7-куб | Усеченный 8-куб |
     |        |          |            |              |                |
Ссылки
- Т. Госсет : О правильных и полуправильных фигурах в пространстве n измерений , Вестник математики, Макмиллан, 1900
- HSM Коксетер :
- Коксетер, Правильные многогранники , (3-е издание, 1973), издание Дувра, ISBN 0-486-61480-8 , стр. 296, Таблица I (iii): Правильные многогранники, три правильных многогранника в n-мерности (n≥5)
- HSM Coxeter, Regular Polytopes , 3-е издание, Dover New York, 1973, стр. 296, Таблица I (iii): Regular Polytopes, три regular polytopes в n-мерностях (n≥5)
- Калейдоскопы: избранные труды Х. С. М. Коксетера , под редакцией Ф. Артура Шерка, Питера МакМаллена, Энтони К. Томпсона, Азии Айвик Вайс, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [1]
- (Документ 22) HSM Coxeter, Правильные и полуправильные многогранники I , [Math. Zeit. 46 (1940) 380-407, MR 2,10]
- (Документ 23) HSM Coxeter, Правильные и полуправильные многогранники II , [Math. Zeit. 188 (1985) 559-591]
- (Документ 24) HSM Coxeter, Правильные и полуправильные многогранники III , [Math. Zeit. 200 (1988) 3-45]
- Джон Х. Конвей , Хайди Бергиел, Хаим Гудман-Штраус, Симметрии вещей 2008, ISBN 978-1-56881-220-5 (Глава 26. стр. 409: Гемикубы: 1 n1 )
- Норман Джонсон Однородные многогранники , Рукопись (1991)
- Н. В. Джонсон: Теория однородных многогранников и сот , доктор философии (1966)
- 2. Выпуклая однородная полихора на основе тессеракта (8-ячейковая) и гексадекахорона (16-ячейковая) - Модель 14, 18, Георгий Ольшевский.
- Клитцинг, Ричард. «Четырехмерные однородные многогранники (полихоры)».o3x3o4x - срит, o3x3x4x - зернистость
- Бумажная модель усеченного тессеракта, созданная с использованием сетей, сгенерированных программой Stella4D



