Кантеллированный 5-клеточный

Ортогональные проекции в плоскости Коксетера A ₄
5-ти ячеечный	Кантеллированный 5-клеточный	Канти-усеченный 5-клеточный

В четырехмерной геометрии 5-ячейка с конической поверхностью — это выпуклый однородный 4-многогранник , представляющий собой коническую поверхность (усечение 2-го порядка, вплоть до рёберного выравнивания) правильной 5-ячейки .

Кантеллированный 5-клеточный

Кантеллированный 5-клеточный
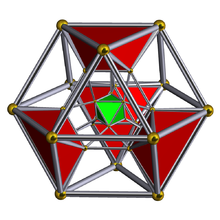Диаграмма Шлегеля с показанными октаэдрическими ячейками
Тип	Однородный 4-многогранник
Символ Шлефли	т _0,2 {3,3,3} рр{3,3,3}
Диаграмма Коксетера
Клетки	20	5 (3.4.3.4) 5 (3.3.3.3) 10 (3.4.4)
Лица	80	50 {3} 30 {4}
Края	90
Вершины	30
Вершинная фигура	Квадратный клин
Группа симметрии	А ₄ , [3,3,3], порядок 120
Характеристики	выпуклый , изогональный
Единый индекс	3 4 5

Кантеллированный 5-ячейковый или малый ромбический пентахорон является однородным 4-многогранником . Он имеет 30 вершин, 90 ребер, 80 граней и 20 ячеек. Ячейки представляют собой 5 кубооктаэдров , 5 октаэдров и 10 треугольных призм . Каждая вершина окружена 2 кубооктаэдрами, 2 треугольными призмами и 1 октаэдром; вершинная фигура представляет собой неоднородную треугольную призму.

Альтернативные названия

Кантеллированный пентахорон
Кантеллированный 4-симплекс
(маленький) призматодиспентахорон
Выпрямленный диспентахорон
Маленький ромбовидный пентахорон (сокращение: Srip) (Джонатан Бауэрс)

Конфигурация

В матрице конфигурации показаны все подсчеты инцидентности между элементами. Диагональные числа f-вектора выводятся с помощью построения Витхоффа , деля полный групповой порядок на подгрупповой порядок, удаляя по одному зеркалу за раз. ^[1]

ф _к	ф ₀	ф ₁		ф ₂				ф ₃
ф ₀	30	2	4	1	4	2	2	2	2	1
ф ₁	2	30	*	1	2	0	0	2	1	0
ф ₁	2	*	60	0	1	1	1	1	1	1
ф ₂	3	3	0	10	*	*	*	2	0	0
	4	2	2	*	30	*	*	1	1	0
	3	0	3	*	*	20	*	1	0	1
	3	0	3	*	*	*	20	0	1	1
ф ₃	12	12	12	4	6	4	0	5	*	*
	6	3	6	0	3	0	2	*	10	*
	6	0	12	0	0	4	4	*	*	5

Изображения

ортографические проекции
Самолет _{Коксетера}	А ₄	А ₃	А ₂
График
Диэдральная симметрия	[5]	[4]	[3]

Каркас	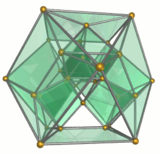Десять треугольных призм зеленого цвета	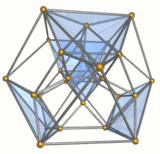Пять октаэдров синего цвета

Координаты

Декартовы координаты вершин конического пятиячейкового многоугольника с центром в начале координат и длиной ребра 2 равны:

Координаты
$\left(2{\sqrt {\frac {2}{5}}},\ 2{\sqrt {\frac {2}{3}}},\ {\frac {1}{\sqrt {3}}},\ \pm 1\right)$ $\left(2{\sqrt {\frac {2}{5}}},\ 2{\sqrt {\frac {2}{3}}},\ {\frac {-2}{\sqrt {3}}},\ 0\right)$ $\left(2{\sqrt {\frac {2}{5}}},\ 0,\ \pm {\sqrt {3}},\ \pm 1\right)$ $\left(2{\sqrt {\frac {2}{5}}},\ 0,\ 0,\ \pm 2\right)$ $\left(2{\sqrt {\frac {2}{5}}},\ -2{\sqrt {\frac {2}{3}}},\ {\frac {2}{\sqrt {3}}},\ 0\right)$ $\left(2{\sqrt {\frac {2}{5}}},\ -2{\sqrt {\frac {2}{3}}},\ {\frac {-1}{\sqrt {3}}},\ \pm 1\right)$ $\left({\frac {-1}{\sqrt {10}}},\ {\sqrt {\frac {3}{2}}},\ \pm {\sqrt {3}},\ \pm 1\right)$	$\left({\frac {-1}{\sqrt {10}}},\ {\sqrt {\frac {3}{2}}},\ 0,\ \pm 2\right)$ $\left({\frac {-1}{\sqrt {10}}},\ {\frac {-1}{\sqrt {6}}},\ {\frac {2}{\sqrt {3}}},\ \pm 2\right)$ $\left({\frac {-1}{\sqrt {10}}},\ {\frac {-1}{\sqrt {6}}},\ {\frac {-4}{\sqrt {3}}},\ 0\right)$ $\left({\frac {-1}{\sqrt {10}}},\ {\frac {-5}{\sqrt {6}}},\ {\frac {1}{\sqrt {3}}},\ \pm 1\right)$ $\left({\frac {-1}{\sqrt {10}}},\ {\frac {-5}{\sqrt {6}}},\ {\frac {-2}{\sqrt {3}}},\ 0\right)$ $\left(-3{\sqrt {\frac {2}{5}}},\ 0,\ 0,\ 0\right)\pm \left(0,\ {\sqrt {\frac {2}{3}}},\ {\frac {2}{\sqrt {3}}},\ 0\right)$ $\left(-3{\sqrt {\frac {2}{5}}},\ 0,\ 0,\ 0\right)\pm \left(0,\ {\sqrt {\frac {2}{3}}},\ {\frac {-1}{\sqrt {3}}},\ \pm 1\right)$

Вершины скошенного 5-ячейника проще всего расположить в 5-мерном пространстве как перестановки:

(0,0,1,1,2)

Эта конструкция основана на положительной ортантной грани скошенного 5-ортоплекса .

Связанные многогранники

Выпуклая оболочка двух скошенных 5-ячеек в противоположных положениях представляет собой неоднородный полихор, состоящий из 100 ячеек: три вида 70 октаэдров (10 выпрямленных тетраэдров, 20 треугольных антипризм, 40 треугольных антиподий), 30 тетраэдров (как тетрагональные двуклиноиды) и 60 вершин. Его вершинная фигура представляет собой форму, топологически эквивалентную кубу с треугольной призмой, прикрепленной к одной из его квадратных граней.

Вершинная фигура

Канти-усеченный 5-клеточный

Канти-усеченный 5-клеточный
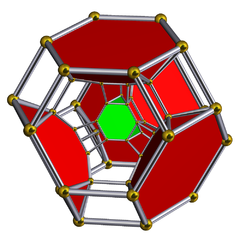Диаграмма Шлегеля с показанными усеченными тетраэдрическими ячейками
Тип	Однородный 4-многогранник
Символ Шлефли	т _0,1,2 {3,3,3} тр{3,3,3}
Диаграмма Коксетера
Клетки	20	5 (4.6.6) 10 (3.4.4) 5 (3.6.6)
Лица	80	20{3} 30{4} 30{6}
Края	120
Вершины	60
Вершинная фигура	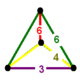клиновидная кость
Группа симметрии	А ₄ , [3,3,3], порядок 120
Характеристики	выпуклый , изогональный
Единый индекс	6 7 8

Кантитруцированный 5-ячейковый или большой ромбический пентахорон является однородным 4-многогранником . Он состоит из 60 вершин, 120 ребер, 80 граней и 20 ячеек. Ячейки: 5 усеченных октаэдров , 10 треугольных призм и 5 усеченных тетраэдров . Каждая вершина окружена 2 усеченными октаэдрами, одной треугольной призмой и одним усеченным тетраэдром.

Конфигурация

В матрице конфигурации показаны все подсчеты инцидентности между элементами. Диагональные числа f-вектора выводятся с помощью построения Витхоффа , деля полный групповой порядок на подгрупповой порядок, удаляя по одному зеркалу за раз. ^[2]

ф _к	ф ₀	ф ₁			ф ₂				ф ₃
ф ₀	60	1	1	2	1	2	2	1	2	1	1
ф ₁	2	30	*	*	1	2	0	0	2	1	0
	2	*	30	*	1	0	2	0	2	0	1
	2	*	*	60	0	1	1	1	1	1	1
ф ₂	6	3	3	0	10	*	*	*	2	0	0
	4	2	0	2	*	30	*	*	1	1	0
	6	0	3	3	*	*	20	*	1	0	1
	3	0	0	3	*	*	*	20	0	1	1
ф ₃	24	12	12	12	4	6	4	0	5	*	*
	6	3	0	6	0	3	0	2	*	10	*
	12	0	6	12	0	0	4	4	*	*	5

Альтернативные названия

Кантиусеченный пентахорон
Усеченный 4-симплекс
Большой призматодиспентахорон
Усеченный диспентахорон
Большой ромбовидный пентахорон (сокращение: рукоятка) (Джонатан Бауэрс)

Изображения

ортографические проекции
Самолет _{Коксетера}	А ₄	А ₃	А ₂
График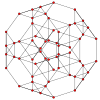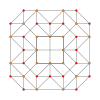
Диэдральная симметрия	[5]	[4]	[3]

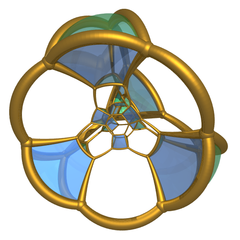Стереографическая проекция с 10 треугольными призмами .

Декартовы координаты

Декартовы координаты усеченного пятиугольника с центром в начале координат и длиной ребра 2 равны:

Координаты
$\left(3{\sqrt {\frac {2}{5}}},\ \pm {\sqrt {6}},\ \pm {\sqrt {3}},\ \pm 1\right)$ $\left(3{\sqrt {\frac {2}{5}}},\ \pm {\sqrt {6}},\ 0,\ \pm 2\right)$ $\left(3{\sqrt {\frac {2}{5}}},\ 0,\ 0,\ 0\right)\pm \left(0,\ {\sqrt {\frac {2}{3}}},\ {\frac {5}{\sqrt {3}}},\ \pm 1\right)$ $\left(3{\sqrt {\frac {2}{5}}},\ 0,\ 0,\ 0\right)\pm \left(0,\ {\sqrt {\frac {2}{3}}},\ {\frac {-1}{\sqrt {3}}},\ \pm 3\right)$ $\left(3{\sqrt {\frac {2}{5}}},\ 0,\ 0,\ 0\right)\pm \left(0,\ {\sqrt {\frac {2}{3}}},\ {\frac {-4}{\sqrt {3}}},\ \pm 2\right)$ $\left({\frac {1}{\sqrt {10}}},\ {\frac {5}{\sqrt {6}}},\ {\frac {5}{\sqrt {3}}},\ \pm 1\right)$ $\left({\frac {1}{\sqrt {10}}},\ {\frac {5}{\sqrt {6}}},\ {\frac {-1}{\sqrt {3}}},\ \pm 3\right)$ $\left({\frac {1}{\sqrt {10}}},\ {\frac {5}{\sqrt {6}}},\ {\frac {-4}{\sqrt {3}}},\ \pm 2\right)$ $\left({\frac {1}{\sqrt {10}}},\ -{\sqrt {\frac {3}{2}}},\ {\sqrt {3}},\ \pm 3\right)$ $\left({\frac {1}{\sqrt {10}}},\ -{\sqrt {\frac {3}{2}}},\ -2{\sqrt {3}},\ 0\right)$ $\left({\frac {1}{\sqrt {10}}},\ {\frac {-7}{\sqrt {6}}},\ {\frac {2}{\sqrt {3}}},\ \pm 2\right)$ $\left({\frac {1}{\sqrt {10}}},\ {\frac {-7}{\sqrt {6}}},\ {\frac {-4}{\sqrt {3}}},\ 0\right)$ $\left(-2{\sqrt {\frac {2}{5}}},\ 2{\sqrt {\frac {2}{3}}},\ {\frac {4}{\sqrt {3}}},\ \pm 2\right)$	$\left(-2{\sqrt {\frac {2}{5}}},\ 2{\sqrt {\frac {2}{3}}},\ {\frac {1}{\sqrt {3}}},\ \pm 3\right)$ $\left(-2{\sqrt {\frac {2}{5}}},\ 2{\sqrt {\frac {2}{3}}},\ {\frac {-5}{\sqrt {3}}},\ \pm 1\right)$ $\left(-2{\sqrt {\frac {2}{5}}},\ 0,\ {\sqrt {3}},\ \pm 3\right)$ $\left(-2{\sqrt {\frac {2}{5}}},\ 0,\ -2{\sqrt {3}},\ 0\right)$ $\left(-2{\sqrt {\frac {2}{5}}},\ -4{\sqrt {\frac {2}{3}}},\ {\frac {1}{\sqrt {3}}},\ \pm 1\right)$ $\left(-2{\sqrt {\frac {2}{5}}},\ -4{\sqrt {\frac {2}{3}}},\ {\frac {-2}{\sqrt {3}}},\ 0\right)$ $\left({\frac {-9}{\sqrt {10}}},\ {\sqrt {\frac {3}{2}}},\ \pm {\sqrt {3}},\ \pm 1\right)$ $\left({\frac {-9}{\sqrt {10}}},\ {\sqrt {\frac {3}{2}}},\ 0,\ \pm 2\right)$ $\left({\frac {-9}{\sqrt {10}}},\ {\frac {-1}{\sqrt {6}}},\ {\frac {2}{\sqrt {3}}},\ \pm 2\right)$ $\left({\frac {-9}{\sqrt {10}}},\ {\frac {-1}{\sqrt {6}}},\ {\frac {-4}{\sqrt {3}}},\ 0\right)$ $\left({\frac {-9}{\sqrt {10}}},\ {\frac {-5}{\sqrt {6}}},\ {\frac {1}{\sqrt {3}}},\ \pm 1\right)$ $\left({\frac {-9}{\sqrt {10}}},\ {\frac {-5}{\sqrt {6}}},\ {\frac {-2}{\sqrt {3}}},\ 0\right)$

Эти вершины можно проще построить на гиперплоскости в 5-мерном пространстве, как перестановки :

(0,0,1,2,3)

Эта конструкция получена из положительной ортантной грани усеченного 5-ортоплекса .

Связанные многогранники

Двойную симметричную конструкцию можно построить, поместив усеченные тетраэдры на усеченные октаэдры, что приведет к неоднородному полихорону с 10 усеченными тетраэдрами , 20 шестиугольными призмами (как дитригональными трапециями), двумя видами 80 треугольных призм (20 с симметрией D _3h и 60 C _2v -симметричными клиньями) и 30 тетраэдрами (как тетрагональными двуклиноидами). Его вершинная фигура топологически эквивалентна октаэдру .

Вершинная фигура

Связанные 4-многогранники

Эти многогранники являются частью набора из 9 однородных 4-мерных многогранников, построенных из группы Коксетера [3,3,3] .

Имя	5-ти ячеечный	усеченный 5-клеточный	выпрямленный 5-элементный	кантеллированный 5-клеточный	усеченный 5-ячеечный	кантит-усеченный 5-клеточный	5-клеточный	runcitucated 5-клеточный	усеченный 5-клеточный
Символ Шлефли	{3,3,3} 3р{3,3,3}	т{3,3,3} 3т{3,3,3}	г{3,3,3} 2г{3,3,3}	рр{3,3,3} р2р{3,3,3}	2т{3,3,3}	тр{3,3,3} т2р{3,3,3}	т _0,3 {3,3,3}	т _0,1,3 {3,3,3} т _0,2,3 {3,3,3}	т _0,1,2,3 {3,3,3}
Диаграмма Коксетера
Диаграмма Шлегеля
Граф плоскости Коксетера ₄
Граф плоскости Коксетера ₃
Граф плоскости Коксетера ₂

Ссылки

^ Клитцинг, Ричард. "o3x4x3o - deca".
^ Клитцинг, Ричард. "x3x4x3o - сцепление".

HSM Коксетер :
- HSM Coxeter, Правильные многогранники , 3-е издание, Довер, Нью-Йорк, 1973 г.
- Калейдоскопы: избранные труды Х. С. М. Коксетера , под редакцией Ф. Артура Шерка, Питера МакМаллена, Энтони К. Томпсона, Азии Айвик Вайс, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [1]
  - (Документ 22) HSM Coxeter, Правильные и полуправильные многогранники I , [Math. Zeit. 46 (1940) 380-407, MR 2,10]
  - (Документ 23) HSM Coxeter, Правильные и полуправильные многогранники II , [Math. Zeit. 188 (1985) 559-591]
  - (Документ 24) HSM Coxeter, Правильные и полуправильные многогранники III , [Math. Zeit. 200 (1988) 3-45]
Норман Джонсон Однородные многогранники , Рукопись (1991)
- Н. В. Джонсон: Теория однородных многогранников и сот , доктор философии (1966)
1. Выпуклая однородная полихора на основе пентахора - Модель 4, 7, Георгий Ольшевский.
Клитцинг, Ричард. «Четырехмерные однородные многогранники (полихоры)».х3о3х3о - срип, х3х3х3о - захват

в т е Фундаментальные выпуклые правильные и однородные многогранники в размерностях 2–10
Семья	А _н	Б _н	Я ₂ (п) / Д _н	Е ₆ / Е ₇ / Е ₈ / Ф ₄ / Соль ₂	Н _н
Правильный многоугольник	Треугольник	Квадрат	п-гон	Шестиугольник	Пентагон
Однородный многогранник	Тетраэдр	Октаэдр • Куб	Демикуб		Додекаэдр • Икосаэдр
Равномерный полихорон	Пентахорон	16-ячеечный • Тессеракт	Демитессеракт	24-ячеечный	120-ячеечный • 600-ячеечный
Однородный 5-многогранник	5-симплекс	5-ортоплекс • 5-куб	5-демикуб
Однородный 6-многогранник	6-симплекс	6-ортоплекс • 6-куб	6-демикуб	1 ₂₂ • 2 ₂₁
Однородный 7-многогранник	7-симплекс	7-ортоплекс • 7-куб	7-демикуб	1 ₃₂ • 2 ₃₁ • 3 ₂₁
Однородный 8-многогранник	8-симплекс	8-ортоплекс • 8-куб	8-демикуб	1 ₄₂ • 2 ₄₁ • 4 ₂₁
Однородный 9-многогранник	9-симплекс	9-ортоплекс • 9-куб	9-демикуб
Однородный 10-многогранник	10-симплекс	10-ортоплекс • 10-куб	10-демикуб
Однородный n - многогранник	н - симплекс	n - ортоплекс • n - куб	н - демикуб	1 _к2 • 2 _к1 • к ₂₁	n - пятиугольный многогранник
Темы: Семейства многогранников • Правильный многогранник • Список правильных многогранников и соединений

[1] Клитцинг, Ричард. "o3x4x3o - deca".

[2] Клитцинг, Ричард. "x3x4x3o - сцепление".