Runcinated 24-клеточный
 24-ячеечный     |  Runcinated 24-ячеечный |
 Runcitucated 24-ячеечный |  Омни-усеченный 24-клеточный (Runcicanti-усеченный 24-клеточный) |
| Ортогональные проекции в плоскости Коксетера F 4 | |
|---|---|
В четырехмерной геометрии 24-ячейковый многогранник с прямой структурой — это выпуклый однородный 4-мерный многогранник , являющийся усечением (обобщением) 24-ячейника с прямой структурой .
Существует 3 уникальных степени рунцинаций 24-клеточного числа, включая перестановки, усечения и сокращения.
Runcinated 24-ячеечный
| Runcinated 24-ячеечный | ||
| Тип | Однородный 4-многогранник | |
| Символ Шлефли | т 0,3 {3,4,3} | |
| Диаграмма Коксетера | | |
| Клетки | 240 | 48 3.3.3.3 192 3.4.4  |
| Лица | 672 | 384{3} 288{4} |
| Края | 576 | |
| Вершины | 144 | |
| Вершинная фигура |  удлиненная квадратная антипризма | |
| Группа симметрии | Аут (F 4 ), [[3,4,3]], заказ 2304 | |
| Характеристики | выпуклый , рёберно-транзитивный | |
| Единый индекс | 25 26 27 | |
В геометрии , 24-ячеечный или малый призматотетраконтоктахорон является однородным 4-многогранником, ограниченным 48 октаэдрами и 192 треугольными призмами . Октаэдрические ячейки соответствуют ячейкам 24-ячеечного и его двойственного.
В 1912 году Э. Л. Элте определил его как полуправильный многогранник.
Альтернативные названия
- Runcinated 24-клеточный ( Норман В. Джонсон )
- рунцинированный икоситтрахорон
- Рулонированный полиоктаэдр
- Малый призматотетраконтоктахорон (спик) (Джонатан Бауэрс)
Координаты
Декартовы координаты 24-клеточного ранцинированного многоугольника с длиной ребра 2 задаются всеми перестановками знака и координат:
- (0, 0, √ 2 , 2+ √ 2 )
- (1, 1, 1+ √ 2 , 1+ √ 2 )
Перестановки второго набора координат совпадают с вершинами вписанного конусообразного тессеракта .
Прогнозы
| самолет Коксетера | Ф 4 | Б 4 |
|---|---|---|
| График | |  |
| Диэдральная симметрия | [[12]] = [24] | [8] |
| самолет Коксетера | Б 3 / А 2 | Б 2 / А 3 |
| График |  |  |
| Диэдральная симметрия | [6] | [[4]] = [8] |
| 3D перспективные проекции | ||
|---|---|---|
 Диаграмма Шлегеля , в центре которой находится октаэдр, с показанными октаэдрами. |  Перспективная проекция 24-ячеечной структуры в трех измерениях, центрированная на октаэдрической ячейке. Вращение касается только 3D-изображения, чтобы показать его структуру, а не вращение в 4-пространстве. Пятнадцать октаэдрических ячеек, обращенных к точке обзора 4D, показаны здесь красным цветом. Промежутки между ними заполнены каркасом из треугольных призм. |  Стереографическая проекция с 24 из 48 октаэдрических ячеек |
Связанный правильный косой многогранник
Правильный косой многогранник , {4,8|3}, существует в 4-пространстве с 8 квадратами вокруг каждой вершины, в зигзагообразной неплоской вершинной фигуре. Эти квадратные грани можно увидеть на усеченном 24-ячейке, использующем все 576 ребер и 288 вершин. 384 треугольных грани усеченного 24-ячейки можно увидеть удаленными. Двойственный правильный косой многогранник, {8,4|3}, аналогичным образом связан с восьмиугольными гранями усеченного 24-ячейки .
Runcitucated 24-ячеечный
| Runcitucated 24-ячеечный | ||
| Тип | Однородный 4-многогранник | |
| Символ Шлефли | т 0,1,3 {3,4,3} с 2,3 {3,4,3} | |
| Диаграмма Коксетера |  | |
| Клетки | 240 | 24 4.6.6  96 4.4.6  96 3.4.4 24 3.4.4.4  |
| Лица | 1104 | 192{3} 720{4} 192{6} |
| Края | 1440 | |
| Вершины | 576 | |
| Вершинная фигура |  Трапециевидная пирамида | |
| Группа симметрии | Ф 4 , [3,4,3], заказ 1152 | |
| Характеристики | выпуклый | |
| Единый индекс | 28 29 30 | |
Усеченный 24-ячеечный или призматоромбатированный икоситетрахорон является однородным 4-многогранником, полученным из 24-ячеечного . Он ограничен 24 усеченными октаэдрами , соответствующими ячейкам 24-ячеечного , 24 ромбокубооктаэдрами , соответствующими ячейкам двойного 24-ячеечного , 96 треугольными призмами и 96 шестиугольными призмами .
Координаты
Декартовы координаты усеченного 24-ячейкового многоугольника с центром в начале координат и длиной ребра 2 задаются всеми перестановками координат и знаком:
- (0, √ 2 , 2 √ 2 , 2+3 √ 2 )
- (1, 1+ √ 2 , 1+2 √ 2 , 1+3 √ 2 )
Перестановки второго набора координат дают вершины вписанного всеусеченного тессеракта .
Двойственная конфигурация имеет координаты, полученные из всех перестановок и знаков:
- (1,1,1+ √ 2 ,5+ √ 2 )
- (1,3,3+ √ 2 ,3+ √ 2 )
- (2,2,2+ √ 2 ,4+ √ 2 )
Прогнозы
| самолет Коксетера | Ф 4 | |
|---|---|---|
| График |  | |
| Диэдральная симметрия | [12] | |
| самолет Коксетера | Б 3 / А 2 (а) | Б 3 / А 2 (б) |
| График |  |  |
| Диэдральная симметрия | [6] | [6] |
| самолет Коксетера | Б 4 | Б 2 / А 3 |
| График |  |  |
| Диэдральная симметрия | [8] | [4] |
 Диаграмма Шлегеля , центрированная на ромбокубооктаэдре, показаны только треугольные призмы |
Runcicantic курносый 24-ячеечный
Полусимметричная конструкция усеченной 24-клеточной структуры (или усеченной 24-клеточной структуры), как, также называемый рунцикантический курносый 24-клеточный , как, имеет идентичную геометрию, но его треугольные грани дополнительно подразделены. Как и у плосконосого 24-клеточного, он имеет симметрию [3 + ,4,3], порядок 576. У усеченного 24-клеточного ранцита есть 192 идентичных шестиугольных грани, в то время как у плосконосого 24-клеточного ранцита есть 2 конструктивных набора из 96 шестиугольников. Различие можно увидеть в вершинных фигурах :
|  |
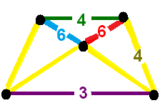Runcic курносый 24-ячеечный
| Runcic курносый 24-ячеечный | ||
|---|---|---|
| Символ Шлефли | с 3 {3,4,3} | |
| Диаграмма Коксетера | | |
| Клетки | 240 | 24 {3,5}  24 т{3,3}  96 (4.4.3) 96 трикап  |
| Лица | 960 | 576 {3} 288 {4} 96 {6} |
| Края | 1008 | |
| Вершины | 288 | |
| Вершинная фигура |  | |
| Группа симметрии | [3 + ,4,3], порядок 576 | |
| Характеристики | выпуклый | |
Родственный 4-политоп — это рунический курносый 24-ячейник или призматоромбиснуб икоситетрахорон , s 3 {3,4,3},. Он не является однородным, но он вершинно-транзитивен и имеет все правильные многоугольные грани. Он построен с 24 икосаэдрами , 24 усеченными тетраэдрами , 96 треугольными призмами и 96 треугольными куполами в зазорах, что в общей сложности составляет 240 ячеек, 960 граней, 1008 ребер и 288 вершин. Как и у плосконосого 24-ячейника , он имеет симметрию [3 + ,4,3], порядок 576. [1]
Вершинная фигура содержит один икосаэдр, две треугольные призмы, один усеченный тетраэдр и 3 треугольных купола.
| Ортографические проекции | Сеть | ||
|---|---|---|---|
 |  |  |  |
Усеченный 24-ячеечный
| Усеченный 24-ячеечный | ||
| Тип | Однородный 4-многогранник | |
| Символ Шлефли | т 0,1,2,3 {3,4,3} | |
| Диаграмма Коксетера | | |
| Клетки | 240 | 48 (4.6.8)  192 (4.4.6) |
| Лица | 1392 | 864 {4} 384 {6} 144 {8} |
| Края | 2304 | |
| Вершины | 1152 | |
| Вершинная фигура |  Филлик дисфеноидный | |
| Группа симметрии | Аут (F 4 ), [[3,4,3]], заказ 2304 | |
| Характеристики | выпуклый | |
| Единый индекс | 29 30 31 | |
Всеусеченный 24-ячеечный или большой призматотетраконтоктахорон является однородным 4-многогранником, полученным из 24-ячеечного . Он состоит из 1152 вершин, 2304 ребер и 1392 граней (864 квадрата, 384 шестиугольника и 144 восьмиугольника). Он имеет 240 ячеек: 48 усеченных кубооктаэдров , 192 шестиугольные призмы . Каждая вершина содержит четыре ячейки в филлической двуклиновидной вершинной фигуре : две шестиугольные призмы и два усеченных кубооктаэдра .
Структура
48 усеченных кубооктаэдрических ячеек соединены друг с другом через их восьмиугольные грани. Их можно сгруппировать в две группы по 24 в каждой, соответствующие ячейкам 24-ячейки и ее двойственной. Промежутки между ними заполнены сетью из 192 шестиугольных призм, соединенных друг с другом через чередующиеся квадратные грани в чередующейся ориентации, а с усеченными кубооктаэдрами через их шестиугольные грани и оставшиеся квадратные грани.
Координаты
Декартовы координаты усеченного 24-клеточного многоугольника с длиной ребра 2 представляют собой перестановки координат и знака:
- (1, 1+ √ 2 , 1+2 √ 2 , 5+3 √ 2 )
- (1, 3+ √ 2 , 3+2 √ 2 , 3+3 √ 2 )
- (2, 2+ √ 2 , 2+2 √ 2 , 4+3 √ 2 )
Изображения
| самолет Коксетера | Ф 4 | Б 4 |
|---|---|---|
| График | |  |
| Диэдральная симметрия | [[12]] = [24] | [8] |
| самолет Коксетера | Б 3 / А 2 | Б 2 / А 3 |
| График |  |  |
| Диэдральная симметрия | [6] | [[4]] = [8] |
| 3D перспективные проекции | |
|---|---|
 Диаграмма Шлегеля |  Перспективная проекция в 3D с центром на усеченном кубооктаэдре. Ближайшая большая ромбокубооктаэдрическая ячейка к точке обзора 4D показана красным, а шесть окружающих ее больших ромбокубооктаэдров — желтым. Двенадцать шестиугольных призм, имеющих общую квадратную грань с ближайшей ячейкой и шестиугольные грани с желтыми ячейками, показаны синим цветом. Остальные ячейки показаны зеленым цветом. Ячейки, лежащие на дальней стороне многогранника с точки обзора 4D, были отброшены для ясности. |
 Усеченный 24-ячеечный |  Двойной к усеченному 24-элементному |
Связанные многогранники
Неоднородные варианты с симметрией [3,4,3] и двумя типами усеченных кубооктаэдров можно удвоить, поместив два типа усеченных кубооктаэдров друг на друга, чтобы получить неоднородный полихор с 48 усеченными кубооктаэдрами , 144 восьмиугольными призмами (как дитетрагональные трапеции), 192 шестиугольными призмами , двумя видами 864 прямоугольных трапеций (288 с симметрией D 2d и 576 с симметрией C 2v ) и 2304 вершинами. Его вершинная фигура — неправильная треугольная бипирамида .
Этот полихорон затем может быть изменен для получения другого неоднородного полихора с 48 плосконосыми кубами , 144 квадратными антипризмами , 192 октаэдрами (как треугольные антипризмы), тремя видами 2016 тетраэдров (288 тетрагональных дисфеноидов, 576 филлиновых дисфеноидов и 1152 неправильных тетраэдра) и 1152 вершинами. Он имеет симметрию [[3,4,3] + ], порядок 1152.
Полный курносый 24-элементный
Однородный плосконосый 24-клеточный называется полуплосконосым 24-клеточным по Джону Хортону Конвею с диаграммой Коксетерав пределах семейства F 4 , хотя это полный курносый или омнисуб в пределах семейства D 4 , как
.
В отличие от этого, полностью плосконосый 24-клеточный или омнисконосый 24-клеточный , определяемый как чередование омниусеченного 24-клеточного, не может быть сделан однородным, но ему можно придать диаграмму Коксетера, и симметрия [[3,4,3]] + , порядок 1152, и построен из 48 плосконосых кубов , 192 октаэдров и 576 тетраэдров, заполняющих пробелы в удаленных вершинах. Его вершинная фигура содержит 4 тетраэдра, 2 октаэдра и 2 плосконосых куба. Он имеет 816 ячеек, 2832 грани, 2592 ребра и 576 вершин. [2]
Связанные многогранники
| 24-ячеечные многогранники семейства | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Имя | 24-ячеечный | усеченный 24-ячеечный | курносый 24-элементный | выпрямленный 24-элементный | кантеллированный 24-ячеечный | битусеченный 24-ячеечный | кантит-усеченный 24-клеточный | 24-клеточный | runcitucated 24-cell | усеченный 24-ячеечный | |
Символ Шлефли | {3,4,3} | т 0,1 {3,4,3} т{3,4,3} | с{3,4,3} | т 1 {3,4,3} р{3,4,3} | т 0,2 {3,4,3} рр{3,4,3} | т 1,2 {3,4,3} 2т{3,4,3} | т 0,1,2 {3,4,3} тр{3,4,3} | т 0,3 {3,4,3} | т 0,1,3 {3,4,3} | т 0,1,2,3 {3,4,3} | |
Диаграмма Коксетера | | | | | | | | | | | |
Диаграмма Шлегеля |  |  |  |  |  |  |  | | | | |
| Ф 4 | |  |  |  |  |  |  | | | | |
| Б 4 |  |  |  |  |  |  |  | | | | |
| Б 3 (а) |  |  |  |  |  |  |  | | | | |
| Б 3 (б) |  |  |  |  |  | | |||||
| Б 2 |  |  |  |  |  |  |  | |  | | |
Примечания
- ^ Клитцинг, Ричард. "s3s4o3x".
- ^ Клитцинг, Ричард. "s3s4s3s".
Ссылки
- Калейдоскопы: избранные труды Х. С. М. Коксетера , под редакцией Ф. Артура Шерка, Питера МакМаллена, Энтони К. Томпсона, Азии Айвик Вайс, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6
- (Документ 22) HSM Coxeter, Правильные и полуправильные многогранники I , [Math. Zeit. 46 (1940) 380-407, MR 2,10]
- (Документ 23) HSM Coxeter, Правильные и полуправильные многогранники II , [Math. Zeit. 188 (1985) 559-591]
- (Документ 24) HSM Coxeter, Правильные и полуправильные многогранники III , [Math. Zeit. 200 (1988) 3-45]
- JH Conway и MJT Guy : Четырехмерные архимедовы многогранники , Труды коллоквиума по выпуклости в Копенгагене, стр. 38 и 39, 1965 г.
- NW Johnson : Теория однородных многогранников и сот , докторская диссертация, Университет Торонто, 1966 г.
- Четырехмерные архимедовы многогранники (на немецком языке), Марко Мёллер, 2004 г. Кандидатская диссертация [1] m58 m59 m53
- 3. Выпуклая однородная полихора на основе икоситетрахорона (24-клеточная), Георгий Ольшевский.
- Клитцинг, Ричард. «Четырехмерные однородные многогранники (полихоры)».x3o4o3x - спик, x3x4o3x - прико, s3s4o3x - присси, x3x4x3x - гиппик
