Дитригональный многогранник
В геометрии существует семь однородных и однородных двойственных многогранников, называемых дитригональными. [1]
Дитригональные вершинные фигуры
Существует пять однородных дитригональных многогранников, все с икосаэдрической симметрией. [1]
Трехмерный звездчатый многогранник с символом Витхоффа в форме 3 | p q или 3/2 | p q являются дитригональными, по крайней мере, если p и q не равны 2. Каждый многогранник включает два типа граней, являющихся треугольниками , пятиугольниками или пентаграммами . Их вершинные конфигурации имеют вид p . q . p . q . p . q или ( p . q ) 3 с симметрией порядка 3. Здесь термин дитригональный относится к шестиугольнику, имеющему симметрию порядка 3 (треугольную симметрию), действующему с 2 вращательными орбитами на 6 углах вершинной фигуры (слово дитригональный означает «имеющий два набора по 3 угла»). [2]
| Тип | Малый дитригональный икосододекаэдр | Дитригональный додекододекаэдр | Большой дитригональный икосододекаэдр |
|---|---|---|---|
| Изображение |  |  |  |
| Вершинная фигура |  |  |  |
| Конфигурация вершины | 3. 5 ⁄ 2 .3. 5 ⁄ 2,3 . 5 ⁄ 2 | 5. 5 ⁄ 3,5 . 5 ⁄ 3,5 . 5 ⁄ 3 | (3.5.3.5.3.5)/2 |
| Лица | 32 20 {3}, 12 { 5 ⁄ 2 } | 24 12 {5}, 12 { 5 ⁄ 2 } | 32 20 {3}, 12 {5} |
| Символ Витхоффа | 3 | 5/2 3 | 3 | 5/3 5 | 3 | 3/2 5 |
| Диаграмма Коксетера | 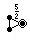 | 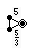 | 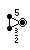 |
Другие однородные дитригональные многогранники
Малый дитригональный додеко-икосододекаэдр и большой дитригональный додеко-икосододекаэдр также являются однородными.
Их двойственными являются соответственно малый дитригональный додекакронный гексаконтаэдр и большой дитригональный додекакронный гексаконтаэдр . [1]
Смотрите также
Ссылки
Примечания
- ^ abc Хар'Эл, 1993
- ^ Uniform Polyhedron, Mathworld (получено 10 июня 2016 г.)
Библиография
- Коксетер, Х. С. М. , Лонге-Хиггинс М. С. и Миллер Дж. К. П., Однородные многогранники, Phil. Trans. 246 A (1954) стр. 401–450.
- Хар'Эл, З. Единообразное решение для однородных многогранников., Geometriae Dedicata 47, 57–110, 1993. Цви Хар'Эл, программное обеспечение Kaleido, изображения, двойные изображения
Дальнейшее чтение
- Джонсон, Н.; Теория однородных многогранников и сот , докторская диссертация, Университет Торонто, 1966 [1]
- Скиллинг, Дж. (1975), «Полный набор однородных многогранников», Philosophical Transactions of the Royal Society of London. Серия A. Математические и физические науки , 278 (1278): 111– 135, Bibcode : 1975RSPTA.278..111S, doi : 10.1098/rsta.1975.0022, ISSN 0080-4614, JSTOR 74475, MR 0365333, S2CID 122634260