Антипризма

Эта статья включает список общих ссылок , но в ней отсутствуют соответствующие встроенные цитаты . Пожалуйста, помогите улучшить эту статью, введя более точные цитаты. ( Январь 2013 ) ( Узнайте, как и когда удалять это сообщение )

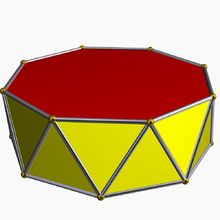
В геометрии n -угольная антипризма или n -антипризма — это многогранник, состоящий из двух параллельных прямых копий (не зеркальных отображений) n -стороннего многоугольника , соединенных чередующейся полосой из 2 n треугольников . Они представлены обозначением Конвея A n .

Антипризмы являются подклассом призматоидов и представляют собой (вырожденный) тип плосконосого многогранника .

Антипризмы похожи на призмы , за исключением того, что основания повернуты относительно друг друга, а боковые грани (соединяющие основания) представляют собой 2n треугольников , а не n четырехугольников .

Двойственный многогранник n -угольной антипризмы является n -угольным трапецоэдром .

В своей книге 1619 года «Harmonices Mundi » Иоганн Кеплер наблюдал существование бесконечного семейства антипризм. ^[1] Это традиционно считается первым открытием этих форм, но они могли быть известны и раньше: неподписанный печатный блок для развёртки шестиугольной антипризмы приписывается Иерониму Андреа , который умер в 1556 году. ^[2]

Немецкая форма слова «антипризма» использовалась для этих форм в 19 веке; Карл Хайнце приписывает ее введение Теодору Виттштейну  [de] . ^[3] Хотя английское «антипризма» использовалось ранее для обозначения оптической призмы, используемой для устранения эффектов первичного оптимального элемента, ^[4] первое использование «антипризмы» в английском языке в его геометрическом смысле, по-видимому, относится к началу 20 века в работах Г. С. М. Коксетера . ^[5]

Для антипризмы с правильными n- угольными основаниями обычно рассматривают случай, когда эти две копии повернуты на угол ⁠180/н⁠ градусов.

Осью правильного многоугольника называется прямая, перпендикулярная плоскости многоугольника и лежащая в его центре.

Для антипризмы с равными правильными n -угольными основаниями, повернутой на угол ⁠180/н⁠ градусов, большая регулярность получается, если основания имеют одну и ту же ось: соосны ; т. е. (для некомпланарных оснований ): если линия, соединяющая центры оснований, перпендикулярна плоскостям оснований. Тогда антипризма называется прямой антипризмой , а ее 2 n боковых граней являются равнобедренными треугольниками .

Однородная n -антипризма имеет два конгруэнтных правильных n -угольника в качестве оснований и 2 n равносторонних треугольников в качестве боковых граней.

Однородные антипризмы образуют бесконечный класс вершинно-транзитивных многогранников, как и однородные призмы. Для n = 2 мы имеем двуугольную антипризму (вырожденную антипризму), которая визуально идентична правильному тетраэдру ; для n = 3 — правильный октаэдр как треугольная антипризма (невырожденная антипризма).

Семейство однородных n- угольных антипризм

• в
• т
• е

Имя антипризмы	Дигональная антипризма	(Треугольная) Треугольная антипризма	(Тетрагональная) Квадратная антипризма	Пятиугольная антипризма	Гексагональная антипризма	Гептагональная антипризма	...	Апейрогональная антипризма
Изображение многогранника							...
Сферическое мозаичное изображение							Изображение мозаики плоскости
Конфигурация вершины.	2.3.3.3	3.3.3.3	4.3.3.3	5.3.3.3	6.3.3.3	7.3.3.3	...	∞.3.3.3

Диаграммы Шлегеля этих полуправильных антипризм следующие:

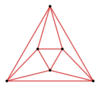А3

А4

А5

А6

А7

А8

Декартовы координаты вершин прямой n -антипризмы (т.е. с правильными n -угольниками в основании и 2 n равнобедренными треугольными боковыми гранями, радиус описанной окружности оснований равен 1) равны:

${\displaystyle \left(\cos {\frac {k\pi }{n}},\sin {\frac {k\pi }{n}},(-1)^{k}h\right)}$

где 0 ≤ k ≤ 2 n – 1 ;

если n -антипризма однородна (т.е. если треугольники равносторонние), то:$${\displaystyle 2h^{2}=\cos {\frac {\pi }{n}}-\cos {\frac {2\pi }{n}}.}$$

Пусть a — длина ребра однородной n- угольной антипризмы; тогда объем равен:$${\displaystyle V={\frac {n{\sqrt {4\cos ^{2}{\frac {\pi }{2n}}-1}}\sin {\frac {3\pi }{2n}}}{12\sin ^{2}{\frac {\pi }{n}}}}~a^{3},}$$

а площадь поверхности равна:$${\displaystyle A={\frac {n}{2}}\left(\cot {\frac {\pi }{n}}+{\sqrt {3}}\right)a^{2}.}$$

Кроме того, объем правильной прямой n-угольной антипризмы с длиной стороны ее основания l и высотой h определяется по формуле:$${\displaystyle V={\frac {nhl^{2}}{12}}\left(\csc {\frac {\pi }{n}}+2\cot {\frac {\pi }{n}}\right).}$$

Радиус описанной горизонтальной окружности правильного -угольника в основании равен${\displaystyle n}$

${\displaystyle R(0)={\frac {l}{2\sin {\frac {\pi }{n}}}}.}$

Вершины основания находятся в

${\displaystyle \left({\begin{array}{c}R(0)\cos {\frac {2\pi m}{n}}\\R(0)\sin {\frac {2\pi m}{n}}\\0\end{array}}\right),\quad m=0..n-1;}$

вершины наверху находятся в

${\displaystyle \left({\begin{array}{c}R(0)\cos {\frac {2\pi (m+1/2)}{n}}\\R(0)\sin {\frac {2\pi (m+1/2)}{n}}\\h\end{array}}\right),\quad m=0..n-1.}$

С помощью линейной интерполяции точки на внешних треугольных ребрах антипризмы, соединяющие вершины внизу с вершинами вверху, находятся в

${\displaystyle \left({\begin{array}{c}{\frac {R(0)}{h}}[(hz)\cos {\frac {2\pi m}{n}}+z\cos {\frac {\pi (2m+1)}{n}}]\\{\frac {R(0)}{h}}[(hz)\sin {\frac {2\pi m}{n}}+z\sin {\frac {\pi (2m+1)}{n}}]\\\\z\end{array}}\right),\quad 0\leq z\leq h,m=0..n-1}$

и в

${\displaystyle \left({\begin{array}{c}{\frac {R(0)}{h}}[(hz)\cos {\frac {2\pi (m+1)}{n}}+z\cos {\frac {\pi (2m+1)}{n}}]\\{\frac {R(0)}{h}}[(hz)\sin {\frac {2\pi (m+1)}{n}}+z\sin {\frac {\pi (2m+1)}{n}}]\\\\z\end{array}}\right),\quad 0\leq z\leq h,m=0..n-1.}$

Построив суммы квадратов координат и в одном из предыдущих двух векторов, квадрат радиуса описанной окружности этого сечения на высоте равен${\displaystyle x}$${\displaystyle у}$${\displaystyle z}$

${\displaystyle R(z)^{2}={\frac {R(0)^{2}}{h^{2}}}[h^{2}-2hz+2z^{2}+2z( hz)\cos {\frac {\pi }{n}}].}$

Горизонтальное сечение на высоте над основанием представляет собой -угольник (усеченный -угольник) со сторонами длины , чередующимися со сторонами длины . (Они выводятся из длины разности предыдущих двух векторов.) Его можно разбить на равнобедренные треугольники с ребрами и (полупериметр ) плюс равнобедренные треугольники с ребрами и (полупериметр ). Согласно формуле Герона площади этих треугольников равны${\displaystyle 0\leq z\leq h}$${\displaystyle 2n}$${\displaystyle n}$${\displaystyle n}$${\displaystyle l_{1}(z)=l(1-z/h)}$${\displaystyle n}$${\displaystyle l_{2}(z)=lz/h}$${\displaystyle n}$${\displaystyle R(z),R(z)}$${\displaystyle l_{1}}$${\displaystyle R(z)+l_{1}(z)/2}$${\displaystyle n}$${\displaystyle R(z),R(z)}$${\displaystyle l_{2}(z)}$${\displaystyle R(z)+l_{2}(z)/2}$

${\displaystyle Q_{1}(z)={\frac {R(0)^{2}}{h^{2}}}(h-z)\left[(h-z)\cos {\frac {\pi }{n}}+z\right]\sin {\frac {\pi }{n}}}$

и

${\displaystyle Q_{2}(z)={\frac {R(0)^{2}}{h^{2}}}z\left[z\cos {\frac {\pi }{n}}+h-z\right]\sin {\frac {\pi }{n}}.}$

Площадь сечения равна , а объем равен${\displaystyle n[Q_{1}(z)+Q_{2}(z)]}$

${\displaystyle V=n\int _{0}^{h}[Q_{1}(z)+Q_{2}(z)]dz={\frac {nh}{3}}R(0)^{2}\sin {\frac {\pi }{n}}(1+2\cos {\frac {\pi }{n}})={\frac {nh}{12}}l^{2}{\frac {1+2\cos {\frac {\pi }{n}}}{\sin {\frac {\pi }{n}}}}.}$

Обратите внимание, что объем прямой n -угольной призмы с теми же l и h равен: что меньше объема антипризмы.$${\displaystyle V_{\mathrm {prism} }={\frac {nhl^{2}}{4}}\cot {\frac {\pi }{n}}}$$

Группа симметрии прямой n -антипризмы (т.е. с правильными основаниями и равнобедренными боковыми гранями) равна D _{n d} = D _{n v} порядка 4 n , за исключением случаев:

• n = 2 : правильный тетраэдр , имеющий большую группу симметрии T _d порядка 24 = 3 × (4 × 2) , которая имеет три версии D _2d в качестве подгрупп;

• n = 3 : правильный октаэдр , имеющий большую группу симметрии O _h порядка 48 = 4 × (4 × 3) , которая имеет четыре версии D _3d в качестве подгрупп.

Группа симметрии содержит инверсию тогда и только тогда, когда n нечетно.

Группа вращения имеет порядок D _n 2 n , за исключением случаев:

• n = 2 : правильный тетраэдр, имеющий большую группу вращения T порядка 12 = 3 × (2 × 2) , которая имеет три версии D ₂ в качестве подгрупп;

• n = 3 : правильный октаэдр, имеющий большую группу вращения O порядка 24 = 4 × (2 × 3) , которая имеет четыре версии D ₃ в качестве подгрупп.

Примечание: Прямые n -антипризмы имеют равные правильные n -угольники в основаниях и равные равнобедренные треугольные боковые грани, поэтому имеют ту же (двугранную) группу симметрии, что и однородная n -антипризма, для n ≥ 4 .

Четырехмерные антипризмы можно определить как имеющие два дуальных многогранника в качестве параллельных противоположных граней, так что каждая трехмерная грань между ними происходит из двух дуальных частей многогранников: вершины и дуального многоугольника, или двух дуальных ребер. Каждый трехмерный выпуклый многогранник комбинаторно эквивалентен одной из двух противоположных граней четырехмерной антипризмы, построенной из ее канонического многогранника и ее полярного дуала. ^[6] Однако существуют четырехмерные полихоры, которые не могут быть объединены со своими дуалами для формирования пятимерных антипризм. ^[7]

3/2-антипризм неоднородный	5/4-антипризм неоднородный	5/2-антипризма	5/3-антипризма
9/2-антипризма	9/4-антипризма	9/5-антипризма

Однородные звездчатые антипризмы называются по их звездчатым многоугольным основаниям, { p / q }, и существуют в прямых и обратных (скрещенных) решениях. Скрещенные формы имеют пересекающиеся вершинные фигуры и обозначаются «перевернутыми» дробями: p /( p – q ) вместо p / q ; например: 5/3 вместо 5/2.

Прямая звездчатая антипризма имеет две конгруэнтные соосные правильные выпуклые или звездчатые многоугольники в основании и 2 n равнобедренных треугольных боковых граней.

Любую звездчатую антипризму с правильными выпуклыми или звездчатыми многоугольными основаниями можно сделать прямой звездчатой ​​антипризмой (перемещая и/или поворачивая одно из ее оснований, если необходимо).

В ретроградных формах, но не в проградных, треугольники, соединяющие выпуклые или звездчатые основания, пересекают ось вращательной симметрии. Таким образом:

• Ретроградные звездчатые антипризмы с основаниями в виде правильных выпуклых многоугольников не могут иметь все равные длины ребер, и поэтому не могут быть однородными. «Исключение»: ретроградная звездчатая антипризма с основаниями в виде равносторонних треугольников (конфигурация вершин: 3,3/2,3,3) может быть однородной; но тогда она имеет вид равностороннего треугольника: это вырожденный звездчатый многогранник.

• Аналогично, некоторые ретроградные звездные антипризмы с правильными звездными многоугольными основаниями не могут иметь все равные длины ребер, и поэтому не могут быть однородными. Пример: ретроградная звездная антипризма с правильными звездными 7/5-угольными основаниями (конфигурация вершин: 3.3.3.7/5) не может быть однородной.

Также можно построить звездные антипризменные соединения с правильными звездными p / q -угольниками, если p и q имеют общие множители. Пример: звездная 10/4-антипризма является соединением двух звездных 5/2-антипризм.

Звезда p / q -антипризмы по симметрии, для p ≤ 12

Группа симметрии	Единые звезды				Правильные звезды
Д 4д [2 + ,8] (2*4)					3.3/2.3.4 Скрещенная квадратная антипризма
Д 5ч [2,5] (*225)	3.3.3.5/2 Пентаграммная антипризма				3.3/2.3.5 скрещенная пятиугольная антипризма
Д 5д [2 + ,10] (2*5)	3.3.3.5/3 Пентаграмма скрещенная антипризма
Д 6д [2 + ,12] (2*6)		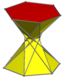			3.3/2.3.6 скрещенная шестиугольная антипризма
Д 7ч [2,7] (*227)	3.3.3.7/2	3.3.3.7/4
Д 7д [2 + ,14] (2*7)	3.3.3.7/3
Д 8д [2 + ,16] (2*8)	3.3.3.8/3 Октаграммная антипризма	3.3.3.8/5 Октаграммная скрещенная антипризма
Д 9ч [2,9] (*229)	3.3.3.9/2 Эннеаграммная антипризма (9/2)	3.3.3.9/4 Эннеаграммная антипризма (9/4)
Д 9д [2 + ,18] (2*9)	3.3.3.9/5 Эннеаграмматическая скрещенная антипризма
Д 10д [2 + ,20] (2*10)	3.3.3.10/3 Декаграммовая антипризма
Д 11ч [2,11] (*2.2.11)	3.3.3.11/2	3.3.3.11/4	3.3.3.11/6
Д 11д [2 + ,22] (2*11)	3.3.3.11/3	3.3.3.11/5	3.3.3.11/7
Д 12д [2 + ,24] (2*12)	3.3.3.12/5	3.3.3.12/7
...	...

• Большая антипризма , четырёхмерный многогранник
• Косой многоугольник — трёхмерный многоугольник, выпуклая оболочка которого является антипризмой.

• Энтони Пью (1976). Многогранники: визуальный подход . Калифорния: Издательство Калифорнийского университета в Беркли. ISBN 0-520-03056-7.Глава 2: Архимедовы многогранники, призмы и антипризмы

• Медиа, связанные с Антипризмами на Wikimedia Commons
• Вайсштейн, Эрик В. «Антипризм». MathWorld .
• Невыпуклые призмы и антипризмы
• Бумажные модели призм и антипризм