Усеченный тессеракт

Тессеракт	Усеченный тессеракт	Выпрямленный тессеракт	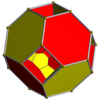Усеченный тессеракт
Диаграммы Шлегеля с центром в [4,3] (ячейки видны в [3,3])
16-ячеечный	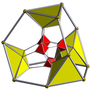Усеченный 16-ячеечный	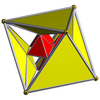Выпрямленный 16-элементный ( 24-элементный )	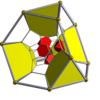Усеченный тессеракт
Диаграммы Шлегеля с центром в [3,3] (ячейки видны в [4,3])

В геометрии усеченный тессеракт — это однородный 4-мерный многогранник , образованный усечением правильного тессеракта .

Существует три усечения, включая битрускление и тритрускление, в результате чего получается усеченный 16-ячейковый массив .

Усеченный тессеракт
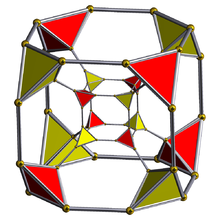Диаграмма Шлегеля ( видны ячейки тетраэдра )
Тип	Однородный 4-многогранник
Символ Шлефли	т{4,3,3}
Диаграммы Коксетера
Клетки	24	8 3.8.8 16 3.3.3
Лица	88	64 {3} 24 {8}
Края	128
Вершины	64
Вершинная фигура	( )v{3}
Двойной	Тетракис 16-клеточный
Группа симметрии	B 4 , [4,3,3], порядок 384
Характеристики	выпуклый
Единый индекс	12 13 14

Усеченный тессеракт ограничен 24 ячейками : 8 усеченными кубами и 16 тетраэдрами .

• Усеченный тессеракт ( Норман У. Джонсон )
• Усеченный тессеракт (сокращение tat) (Джордж Ольшевский и Джонатан Бауэрс) ^[1]

Усеченный тессеракт может быть построен путем усечения вершин тессеракта по длине ребра. В каждой усеченной вершине образуется правильный тетраэдр.${\displaystyle 1/({\sqrt {2}}+2)}$

Декартовы координаты вершин усеченного тессеракта с длиной ребра 2 задаются всеми перестановками:

${\displaystyle \left(\pm 1,\ \pm (1+{\sqrt {2}}),\ \pm (1+{\sqrt {2}}),\ \pm (1+{\sqrt {2}})\right)}$

В первой параллельной проекции усеченного куба усеченного тессеракта в трехмерное пространство изображение располагается следующим образом:

• Проекционная оболочка представляет собой куб .
• Две ячейки усеченного куба проецируются на усеченный куб, вписанный в кубическую оболочку.
• Остальные 6 усеченных кубов выступают на квадратные грани оболочки.
• 8 тетраэдрических объемов между оболочкой и треугольными гранями центрального усеченного куба являются изображениями 16 тетраэдров, по паре ячеек на каждое изображение.

ортографические проекции

самолет Коксетера	Б 4	Б 3 / Д 4 / А 2	Б 2 / Д 3
График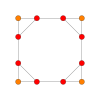
Диэдральная симметрия	[8]	[6]	[4]
самолет Коксетера	Ф 4	А 3
График
Диэдральная симметрия	[12/3]	[4]

Многогранная сетка

Усеченный тессеракт , спроецированный на 3-мерную сферу с помощью стереографической проекции в 3-мерное пространство.

Усеченный тессеракт является третьим в последовательности усеченных гиперкубов :

Усеченные гиперкубы

Изображение								...
Имя	Октагон	Усеченный куб	Усеченный тессеракт	Усеченный 5-куб	Усеченный 6-куб	Усеченный 7-куб	Усеченный 8-куб
Диаграмма Коксетера
Вершинная фигура	( )в( )	( )в{ }	( )v{3}	( )в{3,3}	( )в{3,3,3}	( )в{3,3,3,3}	( )в{3,3,3,3,3}

Усеченный тессеракт
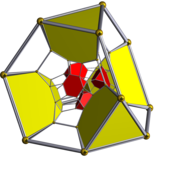Две диаграммы Шлегеля , в центре которых находятся усеченные тетраэдрические или усеченные октаэдрические ячейки, а альтернативные типы ячеек скрыты.
Тип	Однородный 4-многогранник
Символ Шлефли	2т{4,3,3} 2т{3,3 1,1 } ч 2,3 {4,3,3}
Диаграммы Коксетера	=
Клетки	24	8 4.6.6 16 3.6.6
Лица	120	32 {3} 24 {4} 64 {6}
Края	192
Вершины	96
Вершинная фигура	Дигональный двуклиновидный
Группа симметрии	B 4 , [3,3,4], порядок 384 D 4 , [3 1,1,1 ], порядок 192
Характеристики	выпуклый , вершинно-транзитивный
Единый индекс	15 16 17

Тессеракт бит-усеченный , 16-ячеечный бит-усеченный или тессерактигексадекахорон создается с помощью операции бит-усечения, примененной к тессеракту . Его также можно назвать тессерактом-рунцикантом с половиной вершин тессеракта -рунцикантеллата сстроительство.

• Усеченный тессеракт/Ранцикантический тессеракт ( Норман У. Джонсон )
• Тессерактигексадекахорон (сокращение tah) (Джордж Ольшевский и Джонатан Бауэрс) ^[2]

Тессеракт усечен путем усечения его ячеек за пределами их средних точек, превращая восемь кубов в восемь усеченных октаэдров . Они по-прежнему имеют общие квадратные грани, но шестиугольные грани образуют усеченные тетраэдры, которые имеют общие треугольные грани друг с другом.

Декартовы координаты вершин битоусеченного тессеракта с длиной ребра 2 задаются всеми перестановками:

${\displaystyle \left(0,\ \pm {\sqrt {2}},\ \pm 2{\sqrt {2}},\ \pm 2{\sqrt {2}}\right)}$

Усеченные октаэдры соединены друг с другом квадратными гранями, а с усеченными тетраэдрами — шестиугольными гранями. Усеченные тетраэдры соединены друг с другом треугольными гранями.

ортографические проекции

самолет Коксетера	Б 4	Б 3 / Д 4 / А 2	Б 2 / Д 3
График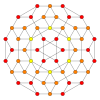
Диэдральная симметрия	[8]	[6]	[4]
самолет Коксетера	Ф 4	А 3
График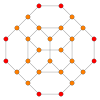
Диэдральная симметрия	[12/3]	[4]

Проекция усеченного октаэдра-первого битусеченного тессеракта в трехмерное пространство имеет усеченную кубическую оболочку. Две усеченные октаэдрические ячейки проецируются на усеченный октаэдр, вписанный в эту оболочку, причем квадратные грани касаются центров октаэдрических граней. 6 октаэдрических граней являются изображениями оставшихся 6 усеченных октаэдрических ячеек. Оставшийся зазор между вписанным усеченным октаэдром и оболочкой заполнен 8 уплощенными усеченными тетраэдрами, каждый из которых является изображением пары усеченных тетраэдрических ячеек.

Стереографические проекции

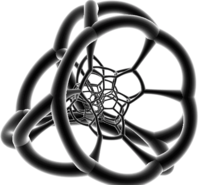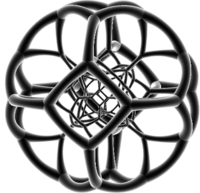Прозрачный с розовыми треугольниками, синими квадратами и серыми шестиугольниками.

Усеченный тессеракт является вторым в последовательности усеченных гиперкубов :

Усеченные гиперкубы

Изображение							...
Имя	Усеченный куб	Усеченный тессеракт	Усеченный 5-кубовый	Усеченный 6-кубовый	Усеченный 7-куб	Усеченный 8-куб
Коксетер
Вершинная фигура	( )в{ }	{ }v{ }	{ }v{3}	{ }v{3,3}	{ }v{3,3,3}	{ }v{3,3,3,3}

Усеченный 16-ячеечный тессеракт Кантика
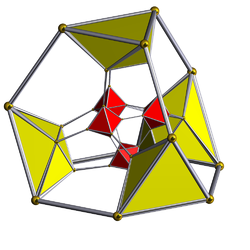Диаграмма Шлегеля ( видны ячейки октаэдра )
Тип	Однородный 4-многогранник
Символ Шлефли	т{4,3,3} т{3,3 1,1 } ч 2 {4,3,3}
Диаграммы Коксетера	=
Клетки	24	8 3.3.3.3 16 3.6.6
Лица	96	64 {3} 32 {6}
Края	120
Вершины	48
Вершинная фигура	квадратная пирамида
Двойной	Тессеракт Гексакиса
Группы Коксетера	B 4 [3,3,4], порядок 384 D 4 [3 1,1,1 ], порядок 192
Характеристики	выпуклый
Единый индекс	16 17 18

Усеченный 16-ячеечный , усеченный гексадекахорон , кантический тессеракт , ограниченный 24 ячейками : 8 правильными октаэдрами и 16 усеченными тетраэдрами . Он имеет половину вершин кантеллированного тессеракта с конструкцией.

Он связан с 24-ячейником , но его не следует путать с ним , который представляет собой правильный 4-ячейниковый многогранник , ограниченный 24 правильными октаэдрами.

• Усеченный 16-ячеечный/Кантический тессеракт ( Норман У. Джонсон )
• Усеченный гексадекахорон (сокращение текc) (Джордж Ольшевский и Джонатан Бауэрс) ^[3]

Усеченная 16-ячейка может быть построена из 16-ячейки путем усечения ее вершин на 1/3 длины ребра. Это дает 16 усеченных тетраэдрических ячеек и вводит 8 октаэдров (вершинные фигуры).

(Усечение 16-ячеечного многоугольника на 1/2 длины ребра приводит к получению 24-ячеечного многоугольника , который имеет большую степень симметрии, поскольку усеченные ячейки становятся идентичными вершинным фигурам.)

Декартовы координаты вершин усеченной 16-клетки с длиной ребра √2 задаются всеми перестановками и комбинациями знаков

(0,0,1,2)

Альтернативная конструкция начинается с полукруглого квадрата с координатами вершин (±3,±3,±3,±3), имеющего четное число каждого знака, и усекает его, чтобы получить перестановки

(1,1,3,3), с четным числом каждого знака.

Усеченные тетраэдры соединены друг с другом посредством своих шестиугольных граней. Октаэдры соединены с усеченными тетраэдрами посредством своих треугольных граней.

Первая параллельная проекция октаэдра усеченного 16-ячейника в трехмерное пространство имеет следующую структуру:

• Проекционная оболочка представляет собой усеченный октаэдр .
• Шесть квадратных граней оболочки являются изображениями шести октаэдрических ячеек.
• Октаэдр лежит в центре оболочки, соединенный с центром 6 квадратных граней 6 ребрами. Это изображение двух других октаэдрических ячеек.
• Оставшееся пространство между оболочкой и центральным октаэдром заполнено 8 усеченными тетраэдрами (искаженными проекцией). Это изображения 16 усеченных тетраэдрических ячеек, по паре ячеек на каждое изображение.

Такое расположение ячеек в проекции аналогично расположению граней в проекции усеченного октаэдра в 2-мерное пространство. Следовательно, усеченный 16-ячейник можно рассматривать как 4-мерный аналог усеченного октаэдра.

Первая параллельная проекция усеченного тетраэдра 16-ячейки в трехмерное пространство имеет следующую структуру:

• Проекционная оболочка представляет собой усеченный куб .
• Ближайший к точке обзора 4D усеченный тетраэдр проецируется в центр оболочки, причем его треугольные грани соединены с 4 октаэдрическими объемами, которые соединяют его с 4 треугольными гранями оболочки.
• Оставшееся пространство в оболочке заполнено четырьмя другими усеченными тетраэдрами.
• Эти объемы представляют собой изображения ячеек, лежащих на ближней стороне усеченной 16-ячеечной структуры; остальные ячейки проецируются на ту же схему, за исключением двойной конфигурации.
• Шесть восьмиугольных граней проекционной оболочки являются изображениями оставшихся 6 усеченных тетраэдрических ячеек.

ортографические проекции

самолет Коксетера	Б 4	Б 3 / Д 4 / А 2	Б 2 / Д 3
График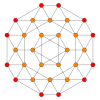
Диэдральная симметрия	[8]	[6]	[4]
самолет Коксетера	Ф 4	А 3
График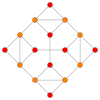
Диэдральная симметрия	[12/3]	[4]

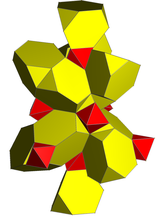Сеть	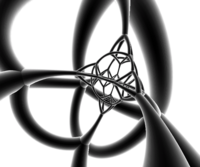Стереографическая проекция (с центром на усеченном тетраэдре )

Усеченный 16-ячейник, как кантический 4-куб, относится к размерному семейству кантических n-кубов:

Размерное семейство кантических n-кубов

н	3	4	5	6	7	8
Симметрия [1 + ,4,3 n-2 ]	[1 + ,4,3] = [3,3]	[1 + ,4,3 2 ] = [3,3 1,1 ]	[1 + ,4,3 3 ] = [3,3 2,1 ]	[1 + ,4,3 4 ] = [3,3 3,1 ]	[1 + ,4,3 5 ] = [3,3 4,1 ]	[1 + ,4,3 6 ] = [3,3 5,1 ]
Кантическая фигура
Коксетер	=	=	=	=	=	=
Шлефли	ч 2 {4,3}	ч 2 {4,3 2 }	ч 2 {4,3 3 }	ч 2 {4,3 4 }	ч 2 {4,3 5 }	ч 2 {4,3 6 }

D 4 равномерная полихора
{3,3 1,1 } ч{4,3,3}	2р{3,3 1,1 } ч 3 {4,3,3}	т{3,3 1,1 } ч 2 {4,3,3}	2т{3,3 1,1 } ч 2,3 {4,3,3}	г{3,3 1,1 } {3 1,1,1 }={3,4,3}	рр{3,3 1,1 } р{3 1,1,1 }=р{3,4,3}	tr{3,3 1,1 } t{3 1,1,1 }=t{3,4,3}	ср{3,3 1,1 } с{3 1,1,1 }=s{3,4,3}

Многогранники симметрии B4
Имя	тессеракт	выпрямленный тессеракт	усеченныйтессеракт	тессеракт с кантеллированными углами	рунический тессеракт	битусеченный тессеракт	усеченный тессеракт	бежатьусеченныйтессеракт ​	омниусеченный тессеракт
Диаграмма Коксетера		=				=
Символ Шлефли	{4,3,3}	т 1 {4,3,3} р{4,3,3}	т 0,1 {4,3,3} т{4,3,3}	т 0,2 {4,3,3} рр{4,3,3}	т 0,3 {4,3,3}	т 1,2 {4,3,3} 2т{4,3,3}	т 0,1,2 {4,3,3} тр{4,3,3}	т 0,1,3 {4,3,3}	т 0,1,2,3 {4,3,3}
Диаграмма Шлегеля
Б 4
Имя	16-ячеечный	выпрямленный 16-элементный	усеченный 16-клеточный	кантеллированный 16-ячеечный	16 -клеточный	усеченный 16-ячеечный	кантит-усеченный 16-клеточный	runcitucated 16-ячеечный	усеченный 16-ячеечный
Диаграмма Коксетера	=	=	=	=		=	=
Символ Шлефли	{3,3,4}	т 1 {3,3,4} р{3,3,4}	т 0,1 {3,3,4} т{3,3,4}	т 0,2 {3,3,4} рр{3,3,4}	т 0,3 {3,3,4}	т 1,2 {3,3,4} 2т{3,3,4}	т 0,1,2 {3,3,4} тр{3,3,4}	т 0,1,3 {3,3,4}	т 0,1,2,3 {3,3,4}
Диаграмма Шлегеля
Б 4

• Т. Госсет : О правильных и полуправильных фигурах в пространстве n измерений , Вестник математики, Макмиллан, 1900
• HSM Коксетер :
  • Коксетер, Правильные многогранники , (3-е издание, 1973), издание Дувра, ISBN  0-486-61480-8 , стр. 296, Таблица I (iii): Правильные многогранники, три правильных многогранника в n-мерности (n≥5)
  • HSM Coxeter, Regular Polytopes , 3-е издание, Dover New York, 1973, стр. 296, Таблица I (iii): Regular Polytopes, три regular polytopes в n-мерностях (n≥5)
  • Калейдоскопы: избранные труды Х. С. М. Коксетера , под редакцией Ф. Артура Шерка, Питера МакМаллена, Энтони К. Томпсона, Азии Айвик Вайс, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [1] 
    • (Документ 22) HSM Coxeter, Правильные и полуправильные многогранники I , [Math. Zeit. 46 (1940) 380-407, MR 2,10]
    • (Документ 23) HSM Coxeter, Правильные и полуправильные многогранники II , [Math. Zeit. 188 (1985) 559-591]
    • (Документ 24) HSM Coxeter, Правильные и полуправильные многогранники III , [Math. Zeit. 200 (1988) 3-45]
• Джон Х. Конвей , Хайди Бергиел, Хаим Гудман-Штраус, Симметрии вещей 2008, ISBN 978-1-56881-220-5 (Глава 26. стр. 409: Гемикубы: 1 _n1 ) 
• Норман Джонсон Однородные многогранники , Рукопись (1991)
  • Н. В. Джонсон: Теория однородных многогранников и сот , доктор философии (1966)
• 2. Выпуклая однородная полихора на основе тессеракта (8-ячейковая) и гексадекахорона (16-ячейковая) - Модели 13, 16, 17, Георгий Ольшевский.
• Клитцинг, Ричард. «Четырехмерные однородные многогранники (полихоры)».о3о3о4о - тат, о3х3х4о - тах, х3х3о4о - тех

• Бумажная модель усеченного тессеракта, созданная с использованием сетей, сгенерированных программой Stella4D