Runcinated 5-клеточный
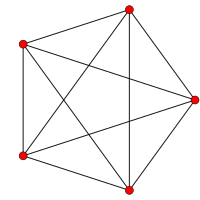Четырехмерный геометрический объект

5-ти ячеечный

Runcinated 5-клеточный

Runcitucated 5-cell

Омниусеченный 5-клеточный
(Runcicantitusercated 5-cell)
Ортогональные проекции в плоскости Коксетера A 4

В четырехмерной геометрии 5-ячейка с рутинным многогранником — это выпуклый однородный 4-многогранник , являющийся рутинизацией (усечением 3-го порядка, с точностью до выравнивания граней ) правильной 5-ячейки .

Существует 3 уникальных степени функционирования пятиклеточного числа, включая перестановки, усечения и сокращения.

Runcinated 5-клеточный

Runcinated 5-клеточный

Диаграмма Шлегеля , на которой видна половина тетраэдрических ячеек.
ТипОднородный 4-многогранник
Символ Шлефлит 0,3 {3,3,3}
Диаграмма Коксетера
Клетки3010 ( 3.3.3 )
20 ( 3.4.4 )
Лица7040 {3}
30 {4}
Края60
Вершины20
Вершинная фигура
(Удлиненная равносторонне-треугольная антипризма)
Группа симметрииАут (А 4 ), [[3,3,3]], порядок 240
Характеристикивыпуклый , изогональный , изотоксальный
Единый индекс4 5 6

Рунцинированный 5-ячеечный или малый призматодекахорон строится путем расширения ячеек 5-ячеечного в радиальном направлении и заполнения промежутков треугольными призмами (которые являются гранными призмами и ребровыми фигурами) и тетраэдрами (ячейками двойственного 5-ячеечного). Он состоит из 10 тетраэдров и 20 треугольных призм. 10 тетраэдров соответствуют ячейкам 5-ячеечного и его двойственного.

Топологически, при его наивысшей симметрии, [[3,3,3]], существует только одна геометрическая форма, содержащая 10 тетраэдров и 20 однородных треугольных призм. Прямоугольники всегда являются квадратами, поскольку две пары ребер соответствуют ребрам двух наборов из 5 правильных тетраэдров каждый в дуальной ориентации, которые становятся равными при расширенной симметрии.

В 1912 году Э. Л. Элте определил его как полуправильный многогранник.

Альтернативные названия

Структура

Две из десяти тетраэдрических ячеек встречаются в каждой вершине. Треугольные призмы лежат между ними, соединенные с ними своими треугольными гранями и друг с другом своими квадратными гранями. Каждая треугольная призма соединена с соседними треугольными призмами в антиориентации (т. е. если ребра A и B в общей квадратной грани соединены с треугольными гранями одной призмы, то это два других ребра соединены с треугольными гранями другой призмы); таким образом, каждая пара соседних призм, если повернуть их в одну и ту же гиперплоскость , образует гиробифастигиум .

Конфигурация

В матрице конфигурации показаны все подсчеты инцидентности между элементами. Диагональные числа f-вектора выводятся с помощью построения Витхоффа , деля полный групповой порядок на подгрупповой порядок, удаляя по одному зеркалу за раз. [1]

ф кф 0ф 1ф 2ф 3
ф 020333631331
ф 1230*2201210
2*300220121
ф 233020**1100
422*30*0110
303**200011
ф 34604005***
663230*10**
636032**10*
406004***5

Вскрытие

Рунцинированный 5-клеточный куб может быть разрезан центральным кубооктаэдром на два тетраэдрических купола . Это разбиение аналогично разбиению трехмерного кубооктаэдра центральным шестиугольником на два треугольных купола .

Изображения

ортографические проекции
Самолет Коксетера
​		А 4А 3А 2
График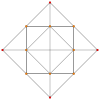
Диэдральная симметрия[[5]] = [10][4][[3]] = [6]

Вид изнутри трехсферной проекции диаграммы Шлегеля с ее 10 тетраэдрическими ячейками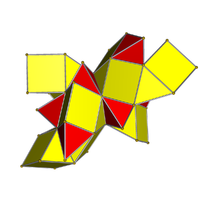
Сеть

Координаты

Декартовы координаты вершин 5-клеточного многогранника с центром в начале координат и длиной ребра 2 равны:

± ( 5 2 ,   1 6 ,   1 3 ,   ± 1 ) {\displaystyle \pm \left({\sqrt {\frac {5}{2}}},\ {\frac {1}{\sqrt {6}}},\ {\frac {1}{\sqrt {3}}},\ \pm 1\right)}
± ( 5 2 ,   1 6 ,   − 2 3 ,   0 ) {\displaystyle \pm \left({\sqrt {\frac {5}{2}}},\ {\frac {1}{\sqrt {6}}},\ {\frac {-2}{\sqrt {3}}},\ 0\right)}
± ( 5 2 ,   − 3 2 ,   0 ,   0 ) {\displaystyle \pm \left({\sqrt {\frac {5}{2}}},\ -{\sqrt {\frac {3}{2}}},\ 0,\ ​​0\right)}
± ( 0 ,   2 2 3 ,   1 3 ,   ± 1 ) {\displaystyle \pm \left(0,\ 2{\sqrt {\frac {2}{3}}},\ {\frac {1}{\sqrt {3}}},\ \pm 1\right)}
± ( 0 ,   2 2 3 ,   − 2 3 ,   0 ) {\displaystyle \pm \left(0,\ 2{\sqrt {\frac {2}{3}}},\ {\frac {-2}{\sqrt {3}}},\ 0\right)}
( 0 ,   0 ,   ± 3 ,   ± 1 ) {\displaystyle \left(0,\ 0,\ ​​\pm {\sqrt {3}},\ \pm 1\right)}
( 0 ,   0 ,   0 ,   ± 2 ) {\displaystyle \left(0,\ 0,\ ​​0,\ ​​\pm 2\right)}

Альтернативный, более простой набор координат может быть создан в 5-мерном пространстве в виде 20 перестановок:

(0,1,1,1,2)

Эта конструкция существует как одна из 32 ортантных граней струйчатого 5-ортоплекса .

Вторая конструкция в 5-пространстве из центра выпрямленного 5-ортоплекса задается перестановками координат:

(1,-1,0,0,0)

Корневые векторы

Его 20 вершин представляют корневые векторы простой группы Ли A 4 . Это также вершинная фигура для 5-клеточных сот в 4-мерном пространстве.

Поперечные сечения

Максимальное поперечное сечение 5-ячейки с 3-мерной гиперплоскостью — кубооктаэдр . Это поперечное сечение делит 5-ячейку с 5 тетраэдрами и 10 треугольными призмами каждый.

Прогнозы

Тетраэдральная ортографическая проекция рунцинированной 5-клетки в 3-мерное пространство имеет кубооктаэдрическую оболочку. Структура этой проекции следующая:

  • Кубооктаэдрическая оболочка разделена внутри следующим образом:
  • Четыре сплющенных тетраэдра соединяют 4 треугольные грани кубооктаэдра с центральным тетраэдром. Это изображения 5 тетраэдрических ячеек.
  • 6 квадратных граней кубооктаэдра соединены с ребрами центрального тетраэдра через искаженные треугольные призмы. Это изображения 6 ячеек треугольной призмы.
  • Остальные 4 треугольные грани соединены с центральным тетраэдром посредством 4 треугольных призм (искаженных проекцией). Это изображения еще 4 ячеек треугольной призмы.
  • Это составляет половину струйчатой ​​пятиячеечной структуры (5 тетраэдров и 10 треугольных призм), которую можно рассматривать как «северное полушарие».
  • Другая половина, «южное полушарие», соответствует изоморфному делению кубооктаэдра в дуальной ориентации, в котором центральный тетраэдр дуален тетраэдру в первой половине. Треугольные грани кубооктаэдра соединяют треугольные призмы в одном полушарии с уплощенными тетраэдрами в другом полушарии, и наоборот. Таким образом, южное полушарие содержит еще 5 тетраэдров и еще 10 треугольных призм, что в сумме составляет 10 тетраэдров и 20 треугольных призм.

Правильный косой многогранник , {4,6|3}, существует в 4-пространстве с 6 квадратами вокруг каждой вершины, в зигзагообразной неплоской вершинной фигуре. Эти квадратные грани можно увидеть на усеченной 5-ячейке, использующей все 60 ребер и 20 вершин. 40 треугольных граней усеченной 5-ячейки можно увидеть удаленными. Двойственный правильный косой многогранник, {6,4|3}, аналогичным образом связан с шестиугольными гранями усеченной 5-ячейки .

Runcitucated 5-cell

Runcitucated 5-cell

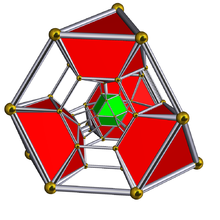Диаграмма Шлегеля с
кубооктаэдрическими ячейками
ТипОднородный 4-многогранник
Символ Шлефлит 0,1,3 {3,3,3}
Диаграмма Коксетера
Клетки305(3.6.6)
10(4.4.6)
10(3.4.4)
5(3.4.3.4)
Лица12040 {3}
60 {4}
20 {6}
Края150
Вершины60
Вершинная фигура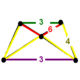
(Прямоугольная пирамида)
Группа КоксетераА 4 , [3,3,3], порядок 120
Характеристикивыпуклый , изогональный
Единый индекс7 8 9
Сеть

Усеченный пятиячеечный или призматоромбатированный пентахорон состоит из 60 вершин, 150 ребер, 120 граней и 30 ячеек. Ячейки: 5 усеченных тетраэдров , 10 шестиугольных призм , 10 треугольных призм и 5 кубооктаэдров . Каждая вершина окружена пятью ячейками: одним усеченным тетраэдром, двумя шестиугольными призмами, одной треугольной призмой и одним кубооктаэдром; вершинная фигура — прямоугольная пирамида.

Альтернативные названия

  • Runcitucated пентахорон
  • Runcitucated 4-симплекс
  • Дипризматодиспентахорон
  • Призматоромбатированный пентахорон (сокращение: prip) (Джонатан Бауэрс)

Конфигурация

В матрице конфигурации показаны все подсчеты инцидентности между элементами. Диагональные числа f-вектора выводятся с помощью построения Витхоффа , деля полный групповой порядок на подгрупповой порядок, удаляя по одному зеркалу за раз. [2]

ф кф 0ф 1ф 2ф 3
ф 060122221211211
ф 1230**220001210
2*60*101101101
2**60010110111
ф 2633020****1100
4202*30***0110
3030**20**1001
4022***30*0101
3003****200011
ф 3126120404005***
1266623030*10**
630603002**10*
120121200464***5

Изображения

ортографические проекции
Самолет Коксетера
​		А 4А 3А 2
График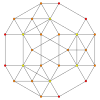
Диэдральная симметрия[5][4][3]

Диаграмма Шлегеля с 40 синими треугольными гранями и 60 зелеными четырехугольными гранями.
Центральная часть диаграммы Шлегеля.

Координаты

Декартовы координаты усеченного пятиугольника с центром в начале координат и длиной ребра 2 равны:

Вершины можно проще построить на гиперплоскости в 5-мерном пространстве, как перестановки :

(0,1,1,2,3)

Эта конструкция представляет собой положительную ортантную грань усеченного 5-ортоплекса .

Усеченный 5-клеточный

Усеченный 5-клеточный

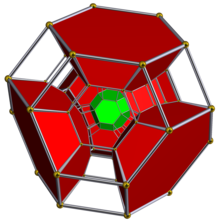Диаграмма Шлегеля , на которой показана половина усеченных октаэдрических ячеек.
ТипОднородный 4-многогранник
Символ Шлефлит 0,1,2,3 {3,3,3}
Диаграмма Коксетера
Клетки3010(4.6.6)
20(4.4.6)
Лица15090{4}
60{6}
Края240
Вершины120
Вершинная фигура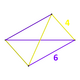
Филлик дисфеноидный
Группа КоксетераАут (А 4 ), [[3,3,3]], порядок 240
Характеристикивыпуклый , изогональный , зонотоп
Единый индекс8 9 10

Всеусеченный 5-клеточный или большой призматодекахорон состоит из 120 вершин, 240 ребер, 150 граней (90 квадратов и 60 шестиугольников ) и 30 ячеек. Ячейки: 10 усеченных октаэдров и 20 шестиугольных призм . Каждая вершина окружена четырьмя ячейками: двумя усеченными октаэдрами и двумя шестиугольными призмами, расположенными в двух филических двуклиновидных вершинных фигурах .

Коксетер называет это многогранником Хинтона в честь CH Hinton , который описал его в своей книге «Четвертое измерение» в 1906 году. Он образует однородные соты, которые Коксетер называет сотами Хинтона . [3]

Альтернативные названия

Конфигурация

В матрице конфигурации показаны все подсчеты инцидентности между элементами. Диагональные числа f-вектора выводятся с помощью построения Витхоффа , деля полный групповой порядок на подгрупповой порядок, удаляя по одному зеркалу за раз. [4]

ф кф 0ф 1ф 2ф 3
ф 012011111111111111
ф 1260***1110001110
2*60**1001101101
2**60*0101011011
2***600010110111
ф 26330020*****1100
42020*30****1010
42002**30***0110
60330***20**1001
40202****30*0101
60033*****200011
ф 32412121204604005***
126606203030*10**
126066033002**10*
240121212000464***5

Изображения

ортографические проекции
Самолет Коксетера
​		А 4А 3А 2
График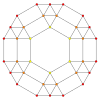
Диэдральная симметрия[[5]] = [10][4][[3]] = [6]
Сеть

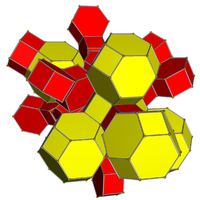Усеченный 5-клеточный
Двойной к усеченному 5-элементному

Перспективные проекции


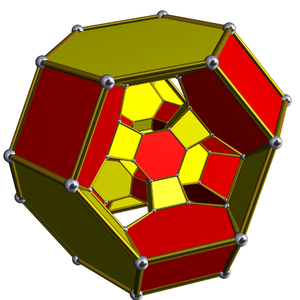Перспективная диаграмма Шлегеля,
центрированная на усеченном октаэдре
Стереографическая проекция

Пермутоэдр

Так же, как усеченный октаэдр является пермутоэдром порядка 4, всеусеченный 5-ячейник является пермутоэдром порядка 5. [5] Всеусеченный 5-ячейник является зонотопом , суммой Минковского пяти отрезков прямых, параллельных пяти линиям, проходящим через начало координат и пять вершин 5-ячейника.

Ортогональная проекция как пермутоэдр

Тесселяции

Усеченная 5-клеточная сота может замостить 4-мерное пространство трансляционными копиями этой ячейки, каждая из которых имеет 3 гиперячейки вокруг каждой грани. Диаграмма Коксетера этой соты :[6] В отличие от аналогичных сот в трех измерениях, битусеченных кубических сот , которые имеют три различные конструкции группы Коксетера Витхоффа , эти соты имеют только одну такую ​​конструкцию. [3]

Симметрия

Всеусеченная 5-ячейка имеет расширенную пентахорическую симметрию, [[3,3,3]], порядок 240. Вершинная фигура всеусеченной 5-ячейки представляет собой тетраэдр Гурса группы Коксетера [3,3,3] . Расширенная симметрия возникает из-за 2-кратного вращения по средней ветви порядка 3 и представляется более явно как [2 + [3,3,3]].

Координаты

Декартовы координаты вершин всеусеченного 5-ячейкового многогранника с центром в начале координат и длиной ребра 2 равны:

( ± 10 ,   ± 6 ,   ± 3 ,   ± 1 ) {\displaystyle \left(\pm {\sqrt {10}},\ \pm {\sqrt {6}},\ \pm {\sqrt {3}},\ \pm 1\right)}
( ± 10 ,   ± 6 ,   0 ,   ± 2 ) {\displaystyle \left(\pm {\sqrt {10}},\ \pm {\sqrt {6}},\ 0,\ \pm 2\right)}
± ( ± 10 ,   2 3 ,   5 3 ,   ± 1 ) {\displaystyle \pm \left(\pm {\sqrt {10}},\ {\sqrt {\frac {2}{3}}},\ {\frac {5}{\sqrt {3}}},\ \pm 1\right)}
± ( ± 10 ,   2 3 ,   − 1 3 ,   ± 3 ) {\displaystyle \pm \left(\pm {\sqrt {10}},\ {\sqrt {\frac {2}{3}}},\ {\frac {-1}{\sqrt {3}}},\ \pm 3\right)}
± ( ± 10 ,   2 3 ,   − 4 3 ,   ± 2 ) {\displaystyle \pm \left(\pm {\sqrt {10}},\ {\sqrt {\frac {2}{3}}},\ {\frac {-4}{\sqrt {3}}},\ \pm 2\right)}
( 5 2 ,   3 3 2 ,   ± 3 ,   ± 1 ) {\displaystyle \left({\sqrt {\frac {5}{2}}},\ 3{\sqrt {\frac {3}{2}}},\ \pm {\sqrt {3}},\ \pm 1\right)}
( − 5 2 ,   − 3 3 2 ,   ± 3 ,   ± 1 ) {\displaystyle \left(-{\sqrt {\frac {5}{2}}},\ -3{\sqrt {\frac {3}{2}}},\ \pm {\sqrt {3}},\ \pm 1\right)}
( 5 2 ,   3 3 2 ,   0 ,   ± 2 ) {\displaystyle \left({\sqrt {\frac {5}{2}}},\ 3{\sqrt {\frac {3}{2}}},\ 0,\ \pm 2\right)}
( − 5 2 ,   − 3 3 2 ,   0 ,   ± 2 ) {\displaystyle \left(-{\sqrt {\frac {5}{2}}},\ -3{\sqrt {\frac {3}{2}}},\ 0,\ \pm 2\right)}
± ( 5 2 ,   1 6 ,   7 3 ,   ± 1 ) {\displaystyle \pm \left({\sqrt {\frac {5}{2}}},\ {\frac {1}{\sqrt {6}}},\ {\frac {7}{\sqrt {3}}},\ \pm 1\right)}
± ( 5 2 ,   1 6 ,   − 2 3 ,   ± 4 ) {\displaystyle \pm \left({\sqrt {\frac {5}{2}}},\ {\frac {1}{\sqrt {6}}},\ {\frac {-2}{\sqrt {3}}},\ \pm 4\right)}
± ( 5 2 ,   1 6 ,   − 5 3 ,   ± 3 ) {\displaystyle \pm \left({\sqrt {\frac {5}{2}}},\ {\frac {1}{\sqrt {6}}},\ {\frac {-5}{\sqrt {3}}},\ \pm 3\right)}
± ( 5 2 ,   − 3 2 ,   ± 2 3 ,   ± 2 ) {\displaystyle \pm \left({\sqrt {\frac {5}{2}}},\ -{\sqrt {\frac {3}{2}}},\ \pm 2{\sqrt {3}},\ \pm 2\right)}
± ( 5 2 ,   − 3 2 ,   0 ,   ± 4 ) {\displaystyle \pm \left({\sqrt {\frac {5}{2}}},\ -{\sqrt {\frac {3}{2}}},\ 0,\ \pm 4\right)}
± ( 5 2 ,   − 7 6 ,   5 3 ,   ± 1 ) {\displaystyle \pm \left({\sqrt {\frac {5}{2}}},\ {\frac {-7}{\sqrt {6}}},\ {\frac {5}{\sqrt {3}}},\ \pm 1\right)}
± ( 5 2 ,   − 7 6 ,   − 1 3 ,   ± 3 ) {\displaystyle \pm \left({\sqrt {\frac {5}{2}}},\ {\frac {-7}{\sqrt {6}}},\ {\frac {-1}{\sqrt {3}}},\ \pm 3\right)}
± ( 5 2 ,   − 7 6 ,   − 4 3 ,   ± 2 ) {\displaystyle \pm \left({\sqrt {\frac {5}{2}}},\ {\frac {-7}{\sqrt {6}}},\ {\frac {-4}{\sqrt {3}}},\ \pm 2\right)}
± ( 0 ,   4 2 3 ,   5 3 ,   ± 1 ) {\displaystyle \pm \left(0,\ 4{\sqrt {\frac {2}{3}}},\ {\frac {5}{\sqrt {3}}},\ \pm 1\right)}
± ( 0 ,   4 2 3 ,   − 1 3 ,   ± 3 ) {\displaystyle \pm \left(0,\ 4{\sqrt {\frac {2}{3}}},\ {\frac {-1}{\sqrt {3}}},\ \pm 3\right)}
± ( 0 ,   4 2 3 ,   − 4 3 ,   ± 2 ) {\displaystyle \pm \left(0,\ 4{\sqrt {\frac {2}{3}}},\ {\frac {-4}{\sqrt {3}}},\ \pm 2\right)}
± ( 0 ,   2 2 3 ,   7 3 ,   ± 1 ) {\displaystyle \pm \left(0,\ 2{\sqrt {\frac {2}{3}}},\ {\frac {7}{\sqrt {3}}},\ \pm 1\right)}
± ( 0 ,   2 2 3 ,   − 2 3 ,   ± 4 ) {\displaystyle \pm \left(0,\ 2{\sqrt {\frac {2}{3}}},\ {\frac {-2}{\sqrt {3}}},\ \pm 4\right)}
± ( 0 ,   2 2 3 ,   − 5 3 ,   ± 3 ) {\displaystyle \pm \left(0,\ 2{\sqrt {\frac {2}{3}}},\ {\frac {-5}{\sqrt {3}}},\ \pm 3\right)}

Эти вершины могут быть проще получены в 5-пространстве как 120 перестановок (0,1,2,3,4). Эта конструкция из положительной ортантной грани ранцикантиусеченного 5-ортоплекса , t 0,1,2,3 {3,3,3,4},.

Неоднородные варианты с симметрией [3,3,3] и двумя типами усеченных октаэдров можно удвоить, поместив два типа усеченных октаэдров друг на друга, чтобы получить неоднородный полихор с 10 усеченными октаэдрами , двумя типами из 40 шестиугольных призм (20 дитригональных призм и 20 дитригональных трапеций), двумя видами из 90 прямоугольных трапеций (30 с симметрией D 2d и 60 с симметрией C 2v ) и 240 вершинами. Его вершинная фигура — неправильная треугольная бипирамида .


Вершинная фигура

Этот полихорон затем может быть изменен для получения другого неоднородного полихорона с 10 икосаэдрами , двумя типами 40 октаэдров (20 с симметрией S 6 и 20 с симметрией D 3 ), тремя типами 210 тетраэдров (30 тетрагональных дисфеноидов, 60 филликовых дисфеноидов и 120 неправильных тетраэдров) и 120 вершинами. Он имеет симметрию [[3,3,3] + ], порядок 120.


Вершинная фигура

Полный курносый 5-элементный

Вершинная фигура для омниснуба 5-клеточного

Полная плосконосая 5-клеточная клетка или омнисконосая 5-клеточная клетка , определяемая как чередование омниусеченной 5-клеточной клетки, не может быть сделана однородной, но ей можно придать диаграмму Коксетера, и симметрия [[3,3,3]] + , порядок 120, и построен из 90 ячеек: 10 икосаэдров , 20 октаэдров и 60 тетраэдров , заполняющих пробелы в удаленных вершинах. Он имеет 300 граней (треугольников), 270 ребер и 60 вершин.

Топологически, при наивысшей симметрии, [[3,3,3]] + , 10 икосаэдров имеют симметрию T (хиральную тетраэдрическую), в то время как 20 октаэдров имеют симметрию D 3 , а 60 тетраэдров имеют симметрию C 2 [7] .

Эти многогранники являются частью семейства из 9 однородных 4-мерных многогранников, построенных на основе группы Коксетера [3,3,3] .

Имя5-ти ячеечныйусеченный 5-клеточныйвыпрямленный 5-элементныйкантеллированный 5-клеточныйусеченный 5-ячеечныйкантит-усеченный 5-клеточный5-клеточныйruncitucated 5-клеточныйусеченный 5-клеточный

Символ Шлефли		{3,3,3}
3р{3,3,3}		т{3,3,3}
2т{3,3,3}		г{3,3,3}
2г{3,3,3}		рр{3,3,3}
р2р{3,3,3}		2т{3,3,3}тр{3,3,3}
т2р{3,3,3}		т 0,3 {3,3,3}т 0,1,3 {3,3,3}
т 0,2,3 {3,3,3}		т 0,1,2,3 {3,3,3}

Диаграмма Коксетера






Диаграмма Шлегеля
Граф плоскости Коксетера 4

Граф плоскости Коксетера 3
Граф плоскости Коксетера 2

Примечания

  1. ^ Клитцинг, Ричард. "x3o3o3x - spid".
  2. ^ Клитцинг, Ричард. "x3x3o3x - прип".
  3. ^ ab Красота геометрии: Двенадцать эссе (1999), Dover Publications, LCCN  99-35678, ISBN 0-486-40919-8 (Классификация зоноэдров, стр. 73) 
  4. ^ Клитцинг, Ричард. "x3x3x3x - gippid".
  5. ^ Пермутаэдр 5-го порядка
  6. ^ Джордж Ольшевский, Однородные паноплоидные тетракомбы , рукопись (2006): Перечисляет мозаику как [140 из 143] Большой призматодекахорный тетракомб (Всеусеченный пентахорный 4d сот)
  7. ^ "С3с3с3с".

Ссылки

  • HSM Коксетер :
    • HSM Coxeter, Правильные многогранники , 3-е издание, Довер, Нью-Йорк, 1973 г.
    • Калейдоскопы: избранные труды Х. С. М. Коксетера , под редакцией Ф. Артура Шерка, Питера МакМаллена, Энтони К. Томпсона, Азии Айвик Вайс, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [1] 
      • (Документ 22) HSM Coxeter, Правильные и полуправильные многогранники I , [Math. Zeit. 46 (1940) 380-407, MR 2,10]
      • (Документ 23) HSM Coxeter, Правильные и полуправильные многогранники II , [Math. Zeit. 188 (1985) 559-591]
      • (Документ 24) HSM Coxeter, Правильные и полуправильные многогранники III , [Math. Zeit. 200 (1988) 3-45]
  • Норман Джонсон Однородные многогранники , Рукопись (1991)
    • Н. В. Джонсон: Теория однородных многогранников и сот , доктор философии.
  • 1. Выпуклая однородная полихора на основе пентахора – модели 5, 8 и 9, Георгий Ольшевский.
  • Клитцинг, Ричард. «Четырехмерные однородные многогранники (полихоры)».o3x3x3o - спид, x3x3o3x - прип, x3x3x3x - гиппид
Фундаментальные выпуклые правильные и однородные многогранники в размерностях 2–10
СемьяА нБ нЯ 2 (п) / Д нЕ 6 / Е 7 / Е 8 / Ф 4 / Соль 2Н н
Правильный многоугольникТреугольникКвадратп-гонШестиугольникПентагон
Однородный многогранникТетраэдрОктаэдр • КубДемикубДодекаэдр • Икосаэдр
Равномерный полихоронПентахорон16-ячеечный • ТессерактДемитессеракт24-ячеечный120-ячеечный • 600-ячеечный
Однородный 5-многогранник5-симплекс5-ортоплекс • 5-куб5-демикуб
Однородный 6-многогранник6-симплекс6-ортоплекс • 6-куб6-демикуб1 22 • 2 21
Однородный 7-многогранник7-симплекс7-ортоплекс • 7-куб7-демикуб1 32 • 2 31 • 3 21
Однородный 8-многогранник8-симплекс8-ортоплекс • 8-куб8-демикуб1 42 • 2 41 • 4 21
Однородный 9-многогранник9-симплекс9-ортоплекс • 9-куб9-демикуб
Однородный 10-многогранник10-симплекс10-ортоплекс • 10-куб10-демикуб
Однородный n - многогранникн - симплексn - ортоплекс • n - кубн - демикуб1 к2 • 2 к1 • к 21n - пятиугольный многогранник
Темы: Семейства многогранников • Правильный многогранник • Список правильных многогранников и соединений
Retrieved from "https://en.wikipedia.org/w/index.php?title=Runcinated_5-cell&oldid=1236328880"