Выпрямленный 600-элементный

Выпрямленный 600-элементный
Диаграмма Шлегеля , показанная как двойная спрямленная 120-ячейковая , с 119 цветными икосаэдрическими ячейками
Тип	Однородный 4-многогранник
Единый индекс	34
Символ Шлефли	т 1 {3,3,5} или г{3,3,5}
Диаграмма Коксетера-Дынкина
Клетки	600 ( 3.3.3.3 ) 120 {3,5}
Лица	1200+2400 {3}
Края	3600
Вершины	720
Вершинная фигура	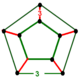пятиугольная призма
Группа симметрии	H 4 , [3,3,5], порядок 14400
Характеристики	выпуклый , вершинно-транзитивный , реберно-транзитивный

В геометрии выпрямленный 600-ячейный или выпрямленный гексакосихорон представляет собой выпуклый однородный 4-многогранник, состоящий из 600 правильных октаэдров и 120 икосаэдрических ячеек . Каждое ребро имеет два октаэдра и один икосаэдр. Каждая вершина имеет пять октаэдров и два икосаэдра. Всего он имеет 3600 треугольных граней, 3600 ребер и 720 вершин.

Содержащий области ячеек как правильного 120-ячеечного , так и правильного 600-ячеечного многогранника, его можно считать аналогом многогранника икосододекаэдра , который является выпрямленным икосаэдром и выпрямленным додекаэдром .

Вершинная фигура выпрямленного 600-ячейника представляет собой однородную пятиугольную призму .

Это один из трех полуправильных 4-многогранников, состоящих из двух или более ячеек, которые являются Платоновыми телами , открытыми Торольдом Госсетом в его статье 1900 года. Он назвал его октикосаэдром , поскольку он состоит из ячеек октаэдра и икосаэдра .

В 1912 году Э. Л. Элте определил его как полуправильный многогранник, обозначив его как tC ₆₀₀ .

• октикосаэдрический (Торолд Госсет)
• Икосаэдрический гексакосигектоникосахорон
• Выпрямленный 600-элементный (Норман В. Джонсон)
• Выпрямленный гексакосихорон
• Выпрямленный политетраэдр
• Рокс (Джонатан Бауэрс)

Ортографические проекции плоскостей Коксетера

Н 4	-	Ф 4
[30]	[20]	[12]
Н 3	А 2 / Б 3 / Д 4	А 3 / Б 2
[10]	[6]	[4]

Стереографическая проекция	Сеть

120-уменьшенный выпрямленный 600-ячеечный
Тип	4-многогранник
Клетки	840 ячеек: 600 квадратная пирамида 120 пятиугольная призма 120 пятиугольная антипризма
Лица	2640: 1800 {3} 600 {4} 240 {5}
Края	2400
Вершины	600
Вершинная фигура	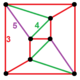Двукратно уменьшенная пятиугольная призма (1) 3.3.3.3 + (4) 3.3.4 (2) 4.4.5 (2) 3.3.3.5
Группа симметрии	1/12[3,3,5], заказ 1200
Характеристики	выпуклый

Связанный вершинно-транзитивный многогранник может быть построен с равными длинами ребер, удаляет 120 вершин из выпрямленного 600-ячейника, но не является однородным, поскольку содержит ячейки квадратной пирамиды , ^[1] открытый Джорджем Ольшевским, назвавшим его swirlprismatodiminished rectified hexacosichoron , с 840 ячейками (600 квадратных пирамид, 120 пятиугольных призм и 120 пятиугольных антипризм), 2640 гранями (1800 треугольников, 600 квадратных и 240 пятиугольников), 2400 ребрами и 600 вершинами. Он имеет хиральную двукратно уменьшенную пятиугольную призму вершинной фигурой .

Каждая удаленная вершина создает ячейку пятиугольной призмы и уменьшает два соседних икосаэдра до пятиугольных антипризм, а каждый октаэдр до квадратной пирамиды. ^[2]

Этот многогранник можно разбить на 12 колец из 10 чередующихся пятиугольных призм и 10 антипризм, а также на 30 колец квадратных пирамид.

Диаграмма Шлегеля	Ортогональная проекция
Показаны два ортогональных кольца.	2 кольца из 30 красных квадратных пирамид, одно кольцо по периметру и одно в центре.

Сеть

Многогранники семейства H 4
120-ячеечный	выпрямленный 120-ячеечный	усеченный 120-ячеечный	кантеллированный 120-ячеечный	120- клеточный	кантит-усеченный 120-ячеечный	runcitucated 120-ячеечный	усеченный 120-ячеечный
{5,3,3}	г{5,3,3}	т{5,3,3}	рр{5,3,3}	т 0,3 {5,3,3}	тр{5,3,3}	т 0,1,3 {5,3,3}	т 0,1,2,3 {5,3,3}
600-ячеечный	выпрямленный600-элементный	усеченный 600-ячеечный	кантеллированный 600-ячеечный	битусжатый 600-ячеечный	усеченный 600-ячеечный	runcitucated 600-ячейковый	усеченный 600-ячеечный
{3,3,5}	г{3,3,5}	т{3,3,5}	рр{3,3,5}	2т{3,3,5}	тр{3,3,5}	т 0,1,3 {3,3,5}	т 0,1,2,3 {3,3,5}

р{п,3,5}

Космос	С 3	Н 3
Форма	Конечный	Компактный		Паракомпактный	Некомпактный
Имя	г{3,3,5}	г{4,3,5}	г{5,3,5}	г{6,3,5}	г{7,3,5}	... г{∞,3,5}
Изображение
Клетки {3,5}	г{3,3}	г{4,3}	г{5,3}	г{6,3}	г{7,3}	г{∞,3}

• Калейдоскопы: избранные труды Х. С. М. Коксетера , под редакцией Ф. Артура Шерка, Питера МакМаллена, Энтони К. Томпсона, Азии Айвик Вайс, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [1] 
  • (Документ 22) HSM Coxeter, Правильные и полуправильные многогранники I , [Math. Zeit. 46 (1940) 380-407, MR 2,10]
  • (Документ 23) HSM Coxeter, Правильные и полуправильные многогранники II , [Math. Zeit. 188 (1985) 559-591]
  • (Документ 24) HSM Coxeter, Правильные и полуправильные многогранники III , [Math. Zeit. 200 (1988) 3-45]
• JH Conway и MJT Guy : Четырехмерные архимедовы многогранники , Труды коллоквиума по выпуклости в Копенгагене, стр. 38 и 39, 1965 г.
• NW Johnson : Теория однородных многогранников и сот , докторская диссертация, Университет Торонто, 1966 г.
• Четырехмерные архимедовы многогранники (на немецком языке), Марко Мёллер, докторская диссертация 2004 г. [2]

• Выпуклая однородная полихора на основе гекатоникосохорона (120-клеточного) и гексакосихорона (600-клеточного) - Модель 34, Георгий Ольшевский.
• Клитцинг, Ричард. «4D однородные многогранники (полихоры) o3x3o5o - rox».
• Archimedisches Polychor Nr. 45 (выпрямленный 600-ячейковый) Архимедовы многогранники Марко Мёллера в R ⁴ (на немецком языке)
• H4 однородные многогранники с координатами: r{3,3,5}