Однородный 6-многогранник

Однородный 6-мерный многогранник

Графы трех правильных и связанных с ними однородных многогранников
6-симплекс	Усеченный 6-симплекс		Выпрямленный 6-симплекс
Кантеллированный 6-симплекс		Runcinated 6-симплекс
Стерилизованный 6-симплекс		Пентеллитный 6-симплекс
6-ортоплекс	Усеченный 6-ортоплекс		Выпрямленный 6-ортоплекс
Корончатый 6-ортоплекс	Runcinated 6-ортоплекс		Стерилизованный 6-ортоплекс
Кантеллированный 6-кубовый		Runcinated 6-кубовый
Стерилизованный 6-кубовый		Пятнистый 6-кубовый
6-кубовый	Усеченный 6-куб		Ректифицированный 6-кубовый
6-демикуб	Усеченный 6-демикуб		Кантеллированный 6-демикуб
Runcinated 6-демикуб		Стерилизованный 6-демикуб
2 ₂₁		1 ₂₂
Усеченный 2 ₂₁		Усеченный 1 ₂₂

В шестимерной геометрии однородный 6-многогранник — это шестимерный однородный многогранник . Однородный многогранник вершинно-транзитивен , и все грани являются однородными 5-многогранниками .

Полный набор выпуклых однородных 6-многогранников не определен, но большинство из них можно построить как конструкции Витхоффа из небольшого набора групп симметрии . Эти операции построения представлены перестановками колец диаграмм Коксетера -Дынкина . Каждая комбинация по крайней мере одного кольца на каждой связанной группе узлов диаграммы дает однородный 6-многогранник.

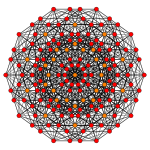
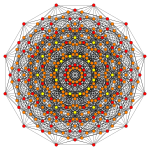
Простейшими однородными многогранниками являются правильные многогранники : 6-симплекс {3,3,3,3,3}, 6-куб (гексакрест) {4,3,3,3,3} и 6-ортоплекс (гексакрест) {3,3,3,3,4}.

История открытия

Правильные многогранники : (выпуклые грани)
- 1852 : Людвиг Шлефли доказал в своей рукописи Theorie der vielfachen Kontinuität , что существует ровно 3 правильных многогранника в 5 или более измерениях .
Выпуклые полуправильные многогранники : (Различные определения до однородной категории Коксетера )
- 1900 : Торольд Госсет перечислил список непризматических полуправильных выпуклых многогранников с правильными гранями (выпуклые правильные многогранники) в своей работе « О правильных и полуправильных фигурах в пространстве n измерений» . ^[1]
Выпуклые однородные многогранники :
- 1940 : Поиск был систематически расширен Г. С. М. Кокстером в его публикации «Правильные и полуправильные многогранники» .
Неправильные однородные звездчатые многогранники : (аналогично невыпуклым однородным многогранникам )
- Продолжается : Джонатан Бауэрс и другие исследователи ищут другие невыпуклые однородные 6-многогранники, с текущим числом 41348 известных однородных 6-многогранников вне бесконечных семейств (выпуклых и невыпуклых), исключая призмы однородных 5-многогранников. Список не доказано полным. ^[2]^[3]

Однородные 6-мерные многогранники по фундаментальным группам Кокстера

Однородные 6-мерные многогранники с отражательной симметрией могут быть получены с помощью этих четырех групп Коксетера, представленных перестановками колец диаграмм Коксетера-Дынкина .

Существует четыре фундаментальные группы отражательной симметрии, которые генерируют 153 уникальных однородных 6-мерных многогранника.

#	Группа Коксетера
1	А ₆	[3,3,3,3,3]
2	Б ₆	[3,3,3,3,4]
3	Д ₆	[3,3,3,3 ^1,1 ]
4	Е ₆	[3 ^2,2,1 ]
4	Е ₆	[3,3 ^2,2 ]

Соответствия диаграмм Коксетера-Дынкина между семействами и более высокая симметрия внутри диаграмм. Узлы одного цвета в каждой строке представляют идентичные зеркала. Черные узлы не активны в соответствии.

Равномерные призматические семейства

Равномерная призма

Существует 6 категориальных однородных призм, основанных на однородных 5-многогранниках .

#	Группа Коксетера		Примечания
1	А ₅ А ₁	[3,3,3,3,2]	Семейство призм на основе 5-симплекса
2	Б ₅ А ₁	[4,3,3,3,2]	Семейство призм на основе 5-куба
3а	Д ₅ А ₁	[3 ^2,1,1 ,2]	Семейство призм на основе 5-демикуба

#	Группа Коксетера		Примечания
4	А ₃ Я ₂ (п)А ₁	[3,3,2,п,2]	Семейство призм на основе тетраэдрических -p-угольных дуопризм
5	Б ₃ Я ₂ (п)А ₁	[4,3,2,п,2]	Семейство призм на основе кубических -p-угольных дуопризм
6	Н ₃ Я ₂ (п)А ₁	[5,3,2,п,2]	Семейство призм на основе додекаэдрических -p-угольных дуопризм

Равномерная дуопризма

Существует 11 категориальных однородных дуопризматических семейств многогранников, основанных на декартовых произведениях однородных многогранников меньшей размерности. Пять из них образованы как произведение однородного 4-мерного многогранника с правильным многоугольником , а шесть образованы произведением двух однородных многогранников :

#	Группа Коксетера		Примечания
1	А ₄ Я ₂ (п)	[3,3,3,2,п]	Семейство на основе 5-клеточных -p-угольных дуопризм.
2	Б ₄ Я ₂ (п)	[4,3,3,2,п]	Семейство на основе тессеракта -p-угольных дуопризм.
3	Ф ₄ И ₂ (п)	[3,4,3,2,п]	Семейство на основе 24-ячеечных -p-угольных дуопризм.
4	Н ₄ Я ₂ (п)	[5,3,3,2,п]	Семейство на основе 120-ячеечных -p-угольных дуопризм.
5	Д ₄ Я ₂ (п)	[3 ^1,1,1 ,2,п]	Семейство на основе полукруглых -p-угольных дуопризм.

#	Группа Коксетера		Примечания
6	А ₃²	[3,3,2,3,3]	Семейство на основе тетраэдрических дуопризм.
7	А ₃ Б ₃	[3,3,2,4,3]	Семейство на основе тетраэдрально - кубических дуопризм.
8	А ₃ Н ₃	[3,3,2,5,3]	Семейство на основе тетраэдрических - додекаэдрических дуопризмов.
9	Б ₃²	[4,3,2,4,3]	Семейство на основе кубических дуопризм.
10	Б ₃ Н ₃	[4,3,2,5,3]	Семейство на основе кубо - додекаэдрических дуопризм.
11	Н ₃²	[5,3,2,5,3]	Семейство на основе додекаэдрических дуопризм.

Равномерный триапризма

Существует одно бесконечное семейство однородных триапризматических семейств многогранников, построенных как декартово произведение трех правильных многоугольников. Каждая комбинация по крайней мере одного кольца на каждой связной группе производит однородный призматический 6-многогранник.

#	Группа Коксетера			Примечания
1	Я ₂ (п)Я ₂ (к)Я ₂ (р)	[п,2,д,2,р]		Семейство на основе p,q,r-угольных трипризм

Перечисление выпуклых однородных 6-мерных многогранников

Симплексная семья: A ₆ [3 ⁴ ] -
- 35 однородных 6-мерных многогранников как перестановки колец в групповой диаграмме, включая один правильный:
  1. {3 ⁴ } - 6-симплекс -
Семейство гиперкубов / ортоплексов : B ₆ [4,3 ⁴ ] -
- 63 однородных 6-мерных многогранника как перестановки колец в групповой диаграмме, включая две правильные формы:
  1. {4,3 ³ } — 6-куб (гексагон) -
  2. {3 ³ ,4} — 6-ортоплекс , (гексакрест) -
Семейство полугиперкубов D ₆ : [3 ^3,1,1 ] -
- 47 однородных 6-мерных многогранников (16 уникальных) как перестановки колец в групповой диаграмме, в том числе:
  1. {3,3 ^2,1 }, 1 ₂₁ 6-демикуб (демигексацикл) -; также как h{4,3 ³ },
  2. {3,3,3 ^1,1 }, 2 ₁₁ 6-ортоплекс -, полусимметричная форма.
Семейство E ₆ : [3 ^3,1,1 ] -
- 39 однородных 6-мерных многогранников как перестановки колец в групповой диаграмме, в том числе:
  1. {3,3,3 ^2,1 }, 2 ₂₁ -
  2. {3,3 ^2,2 }, 1 ₂₂ -

Эти фундаментальные семейства порождают 153 непризматических выпуклых однородных полипэта.

Кроме того, существует 57 однородных 6-политопических конструкций, основанных на призмах однородных 5-политопов : [3,3,3,3,2], [4,3,3,3,2], [3 ^2,1,1 ,2], за исключением пентерактной призмы как дубликата гексеракта.

Кроме того, существует бесконечно много однородных 6-мерных многогранников, основанных на:

Семейства призм дуопризм: [3,3,2,p,2], [4,3,2,p,2], [5,3,2,p,2].
Семейства дуопризм: [3,3,3,2,p], [4,3,3,2,p], [5,3,3,2,p].
Семейство трипризм: [p,2,q,2,r].

А₆семья

Существует 32+4−1=35 форм, полученных путем маркировки одного или нескольких узлов диаграммы Коксетера-Дынкина . Все 35 перечислены ниже. Они названы Норманом Джонсоном по операциям построения Витхоффа на регулярном 6-симплексе (гептапетоне). Названия сокращений в стиле Боуэрса даны в скобках для перекрестных ссылок.

Семейство A ₆ имеет симметрию порядка 5040 (7- факториал ).

Координаты однородных 6-многогранников с 6-симплексной симметрией могут быть получены как перестановки простых целых чисел в 7-мерном пространстве, все в гиперплоскостях с нормальным вектором (1,1,1,1,1,1,1).

#	Коксетер-Дынкин	Система наименований Джонсона Имя Боуэрса и (аббревиатура)	Базовая точка	Количество элементов
#	Коксетер-Дынкин	Система наименований Джонсона Имя Боуэрса и (аббревиатура)	Базовая точка	5	4	3	2	1	0
1		6-симплексный гептапетон (хмель)	(0,0,0,0,0,0,1)	7	21	35	35	21	7
2		Ректифицированный 6-симплекс ректифицированный гептапетон (рил)	(0,0,0,0,0,1,1)	14	63	140	175	105	21
3		Усеченный 6-симплексный усеченный гептапетон (til)	(0,0,0,0,0,1,2)	14	63	140	175	126	42
4		Биректифицированный 6-симплексный биректифицированный гептапетон (бриль)	(0,0,0,0,1,1,1)	14	84	245	350	210	35
5		Кантеллированный 6-симплексный малый ромбический гептапетон (sril)	(0,0,0,0,1,1,2)	35	210	560	805	525	105
6		Усеченный 6-симплексный усеченный гептапетон (батал)	(0,0,0,0,1,2,2)	14	84	245	385	315	105
7		Кантитруцированный 6-симплексный большой ромбический гептапетон (gril)	(0,0,0,0,1,2,3)	35	210	560	805	630	210
8		Runcinated 6-симплексный малый призматический гептапетон (spil)	(0,0,0,1,1,1,2)	70	455	1330	1610	840	140
9		Двояковыпуклый 6-симплексный малый биромбатный гептапетон (сабрил)	(0,0,0,1,1,2,2)	70	455	1295	1610	840	140
10		Ранцитусечённый 6-симплексный призматоусечённый гептапетон (патальный)	(0,0,0,1,1,2,3)	70	560	1820	2800	1890	420
11		Три-усеченный 6-симплекс тетрадекапетон (fe)	(0,0,0,1,2,2,2)	14	84	280	490	420	140
12		Runcicantellated 6-симплекс призматорогомбированный гептапетон (pril)	(0,0,0,1,2,2,3)	70	455	1295	1960	1470	420
13		Бикантиусечённый 6-симплексный большой биромбатный гептапетон (габрил)	(0,0,0,1,2,3,3)	49	329	980	1540	1260	420
14		Рунцикантиусеченный 6-симплексный большой призматический гептапетон (гапил)	(0,0,0,1,2,3,4)	70	560	1820	3010	2520	840
15		Стерильный 6-симплексный мелкоклеточный гептапетон (чешуйка)	(0,0,1,1,1,1,2)	105	700	1470	1400	630	105
16		Двуручьевой 6-симплексный малый бипризмато-тетрадекапетон (sibpof)	(0,0,1,1,1,2,2)	84	714	2100	2520	1260	210
17		Стеритруркированный 6-симплексный целлюлитруткрированный гептапетон (катализ)	(0,0,1,1,1,2,3)	105	945	2940	3780	2100	420
18		Стерильноклеточный 6-симплексный ромбовидный гептапетон (cral)	(0,0,1,1,2,2,3)	105	1050	3465	5040	3150	630
19		Бирунцитусечённый 6-симплексный бипризматоргомбированный гептапетон (баприл)	(0,0,1,1,2,3,3)	84	714	2310	3570	2520	630
20		Стерикантитруцированный 6-симплексный клеточный генератор гомбированный гептапетон (каграл)	(0,0,1,1,2,3,4)	105	1155	4410	7140	5040	1260
21		Стерилизованный 6-симплексный клеточно-призматический гептапетон (копал)	(0,0,1,2,2,2,3)	105	700	1995	2660	1680	420
22		Sterirunciturcated 6-simplex celliprismatotruncated heptapeton (captal)	(0,0,1,2,2,3,4)	105	945	3360	5670	4410	1260
23		Стерилизованный 6-симплексный клеточно-призматический гомбированный гептапетон (коприл)	(0,0,1,2,3,3,4)	105	1050	3675	5880	4410	1260
24		Бирунцикантиусеченный 6-симплексный большой бипризмато-тетрадекапетон (гибпоф)	(0,0,1,2,3,4,4)	84	714	2520	4410	3780	1260
25		Стерирунцикантитрированный 6-симплексный большой клеточный гептапетон (гакал)	(0,0,1,2,3,4,5)	105	1155	4620	8610	7560	2520
26		Пентеллированный 6-симплексный малый тери-тетрадекапетон (посох)	(0,1,1,1,1,1,2)	126	434	630	490	210	42
27		Пентиусеченный 6-симплексный терракотовый гептапетон (токал)	(0,1,1,1,1,2,3)	126	826	1785	1820	945	210
28		Пятилучевой 6-симплексный терипризматический гептапетон (топал)	(0,1,1,1,2,2,3)	126	1246	3570	4340	2310	420
29		Пентикантитрусцированный 6-симплексный теригреаторромбированный гептапетон (тограл)	(0,1,1,1,2,3,4)	126	1351	4095	5390	3360	840
30		Пентирунцитусечённый 6-симплексный терицеллиромбированный гептапетон (токрал)	(0,1,1,2,2,3,4)	126	1491	5565	8610	5670	1260
31		Пентирунцикантеллированный 6-симплексный терипризматоромби-тетрадекапетон (тапорф)	(0,1,1,2,3,3,4)	126	1596	5250	7560	5040	1260
32		Пентирунцикантиусечённый 6-симплексный теригреатопризматичный гептапетон (тагопал)	(0,1,1,2,3,4,5)	126	1701	6825	11550	8820	2520
33		Пентистеритусеченный 6-симплекс терицеллитрунки-тетрадекапетон (тактаф)	(0,1,2,2,2,3,4)	126	1176	3780	5250	3360	840
34		Пентистерикантитусеченный 6-симплексный терицеллигреатор ромбовидный гептапетон (такограл)	(0,1,2,2,3,4,5)	126	1596	6510	11340	8820	2520
35		Всеусеченный 6-симплексный большой тери-тетрадекапетон (готаф)	(0,1,2,3,4,5,6)	126	1806	8400	16800	15120	5040

Б₆семья

Существует 63 формы, основанные на всех перестановках диаграмм Кокстера-Дынкина с одним или несколькими кольцами.

Семейство B ₆ имеет симметрию порядка 46080 (6 факториал x 2 ⁶ ).

Они названы Норманом Джонсоном из строительных операций Wythoff на регулярном 6-кубе и 6-ортоплексе. Имена Боуэрса и сокращенные названия даны для перекрестных ссылок.

#	Диаграмма Коксетера-Дынкина	Символ Шлефли	Имена	Количество элементов
#	Диаграмма Коксетера-Дынкина	Символ Шлефли	Имена	5	4	3	2	1	0
36		т ₀ {3,3,3,3,4}	6-ортоплекс гексаконтатетрапетон (джи)	64	192	240	160	60	12
37		т ₁ {3,3,3,3,4}	Ректифицированный 6-ортоплекс Ректифицированный гексаконтатетрапетон (тряпка)	76	576	1200	1120	480	60
38		т ₂ {3,3,3,3,4}	Биректифицированный 6-ортоплекс Биректифицированный гексаконтатетрапетон (браг)	76	636	2160	2880	1440	160
39		т ₂ {4,3,3,3,3}	Двунаправленный 6-кубовый Двунаправленный гексеракт (брокс)	76	636	2080	3200	1920	240
40		т ₁ {4,3,3,3,3}	Выпрямленный 6-кубовый Выпрямленный гексагон (rax)	76	444	1120	1520	960	192
41		т ₀ {4,3,3,3,3}	6-кубовый гексагон (топор)	12	60	160	240	192	64
42		т _0,1 {3,3,3,3,4}	Усеченный 6-ортоплекс Усеченный гексаконтатетрапетон (тег)	76	576	1200	1120	540	120
43		т _0,2 {3,3,3,3,4}	Кантеллированный 6-ортоплекс Малый ромбированный гексаконтатетрапетон (srog)	136	1656	5040	6400	3360	480
44		т _1,2 {3,3,3,3,4}	Усеченный 6-ортоплекс Усеченный гексаконтатетрапетон (ботаг)					1920	480
45		т _0,3 {3,3,3,3,4}	Runcinated 6-ortoplex Малый призматический гексаконтатетрапетон (spog)					7200	960
46		т _1,3 {3,3,3,3,4}	Двояковыпуклый 6-ортоплекс Малый биромбатный гексаконтатетрапетон (сиборг)					8640	1440
47		т _2,3 {4,3,3,3,3}	Три-усеченный 6-кубовый гексарактигексаконтитетрапетон (xog)					3360	960
48		т _0,4 {3,3,3,3,4}	Стерильный 6-ортоплекс Мелкоклеточный гексаконтатетрапетон (скаг)					5760	960
49		т _1,4 {4,3,3,3,3}	Бирунцинированный 6-кубовый Малый бипризмато-гексарактигексаконтитетрапетон (собпоксог)					11520	1920
50		т _1,3 {4,3,3,3,3}	Двояковыпуклый 6-кубовый Малый биромбатный гексагон (саборкс)					9600	1920
51		т _1,2 {4,3,3,3,3}	Бит-утраченный 6-кубовый Бит -утраченный гексагон (ботокс)					2880	960
52		т _0,5 {4,3,3,3,3}	Пентеллированный 6-кубовый Малый тери-гексерактигексаконтитетрапетон (стоксог)					1920	384
53		т _0,4 {4,3,3,3,3}	Стерилизованный 6-кубовый Малый ячеистый гексагон (scox)					5760	960
54		т _0,3 {4,3,3,3,3}	Runcinated 6-кубовый Малый призматический гексагон (spox)					7680	1280
55		т _0,2 {4,3,3,3,3}	Кантеллированный 6-кубовый Малый ромбический шестигранник (srox)					4800	960
56		т _0,1 {4,3,3,3,3}	Усеченный 6-кубовый Усеченный гексагон (токс)	76	444	1120	1520	1152	384
57		т _0,1,2 {3,3,3,3,4}	Кантитруцированный 6-ортоплекс Большой ромбированный гексаконтатетрапетон (шамот)					3840	960
58		т _0,1,3 {3,3,3,3,4}	Runciturcated 6-ortoplex Prismatotruncated hexacontatetrapeton (potag)					15840	2880
59		т _0,2,3 {3,3,3,3,4}	Runcicantellated 6-ortoplex Призматрономбатированный гексаконтатетрапетон (prog)					11520	2880
60		т _1,2,3 {3,3,3,3,4}	Бикантиусечённый 6-ортоплекс Большой биромбатный гексаконтатетрапетон (габорг)					10080	2880
61		т _0,1,4 {3,3,3,3,4}	Стеритрункированный 6-ортоплекс Целлитрункированный гексаконтатетрапетон (catog)					19200	3840
62		т _0,2,4 {3,3,3,3,4}	Стерилизованный 6-ортоплексный целлиромбированный гексаконтатетрапетон (скала)					28800	5760
63		т _1,2,4 {3,3,3,3,4}	Бирунцитусечённый 6-ортоплекс Бипризматоусечённый гексаконтатетрапетон (бопракс)					23040	5760
64		т _0,3,4 {3,3,3,3,4}	Стерилизованный 6-ортоплексный целлипризмированный гексаконтатетрапетон (копог)					15360	3840
65		т _1,2,4 {4,3,3,3,3}	Бирунцитусечённый 6-кубовый Бипризматоусечённый гексагон (бопраг)					23040	5760
66		т _1,2,3 {4,3,3,3,3}	Бикантиусечённый 6-кубический Большой биромбатный гексагон (габоркс)					11520	3840
67		т _0,1,5 {3,3,3,3,4}	Пентиусеченный 6-ортоплекс Теритусеченный гексаконтатетрапетон (такокс)					8640	1920
68		т _0,2,5 {3,3,3,3,4}	Пентикантеллированный 6-ортоплекс Терирромбированный гексаконтатетрапетон (тапокс)					21120	3840
69		т _0,3,4 {4,3,3,3,3}	Стерилизованный 6-кубовый целлипризматический гексагон (копокс)					15360	3840
70		т _0,2,5 {4,3,3,3,3}	Пятиконечный 6-кубовый Териромбатированный гексагон (топаз)					21120	3840
71		т _0,2,4 {4,3,3,3,3}	Стерилизованный 6-кубовый целлофановый гексагональный гексагон (crax)					28800	5760
72		т _0,2,3 {4,3,3,3,3}	Рунцикантеллированный 6-кубовый призматический ромбовидный гексагон (прокси)					13440	3840
73		т _0,1,5 {4,3,3,3,3}	Пентиусеченный 6-кубовый Теритусеченный гексагон (таког)					8640	1920
74		т _0,1,4 {4,3,3,3,3}	Стеритрункированный 6-кубовый Целлюлтрункированный гексагон (катакс)					19200	3840
75		т _0,1,3 {4,3,3,3,3}	Runciturcated 6-cube Prismatotruncated hexeract (potax)					17280	3840
76		т _0,1,2 {4,3,3,3,3}	Усеченный 6-кубовый Большой ромбический гексагон (грокс)					5760	1920
77		т _0,1,2,3 {3,3,3,3,4}	Рунцикантиусеченный 6-ортоплексный Большой призматический гексаконтатетрапетон (гопог)					20160	5760
78		т _0,1,2,4 {3,3,3,3,4}	Стерикантитруцированный 6-ортоплекс Целлигреаторгомбированный гексаконтатетрапетон (кагорг)					46080	11520
79		т _0,1,3,4 {3,3,3,3,4}	Стерирунцитоусеченный 6-ортоплекс Целлипризматоусеченный гексаконтатетрапетон (каптог)					40320	11520
80		т _0,2,3,4 {3,3,3,3,4}	Стерилизованный 6-ортоплексный целлипризматоргомбированный гексаконтатетрапетон (копраг)					40320	11520
81		т _1,2,3,4 {4,3,3,3,3}	Бирунцикантиусеченный 6-кубовый Большой бипризмато-гексарактигексаконтитетрапетон (gobpoxog)					34560	11520
82		т _0,1,2,5 {3,3,3,3,4}	Пентикантитрукцированный 6-ортоплекс Теригреаторромбированный гексаконтатетрапетон (тогриг)					30720	7680
83		т _0,1,3,5 {3,3,3,3,4}	Пентирунцитусечённый 6-ортоплекс Терипризматоусечённый гексаконтатетрапетон (токракс)					51840	11520
84		т _0,2,3,5 {4,3,3,3,3}	Пентирунцикантеллированный 6-кубовый Терипризматоромби-гексарактигексаконтитетрапетон (типриксог)					46080	11520
85		т _0,2,3,4 {4,3,3,3,3}	Стерилизованный 6-кубовый целлипризматический гомбированный гексагон (coprix)					40320	11520
86		т _0,1,4,5 {4,3,3,3,3}	Пентистеритусеченный 6-кубовый Теричелли-гексерактигексаконтитетрапетон (тактаксог)					30720	7680
87		т _0,1,3,5 {4,3,3,3,3}	Пентирунциусеченный 6-кубовый Терипризматоусеченный гексагон (токраг)					51840	11520
88		т _0,1,3,4 {4,3,3,3,3}	Стерирунцитоусеченный 6-кубовый Целлипризматоусеченный гексагон (captix)					40320	11520
89		т _0,1,2,5 {4,3,3,3,3}	Пентикантитрукцированный 6-кубовый Теригреаторромбированный гексагонакт (тогрикс)					30720	7680
90		т _0,1,2,4 {4,3,3,3,3}	Стерикантитруцированный 6-кубовый Celligeatorhombated hexeract (cagorx)					46080	11520
91		т _0,1,2,3 {4,3,3,3,3}	Рунцикантиусеченный 6-кубовый Большой призматический гексагон (гиппокс)					23040	7680
92		т _0,1,2,3,4 {3,3,3,3,4}	Стерирунцикантитрированный 6-ортоплекс Большой клеточный гексаконтатетрапетон (гоког)					69120	23040
93		т _0,1,2,3,5 {3,3,3,3,4}	Пентирунцикантиусеченный 6-ортоплексный Теригреатопризматизированный гексаконтатетрапетон (тагпог)					80640	23040
94		т _0,1,2,4,5 {3,3,3,3,4}	Пентистерическийантитрукцированный 6-ортоплекс Терицеллигреаторогомбатированный гексаконтатетрапетон (текагорг)					80640	23040
95		т _0,1,2,4,5 {4,3,3,3,3}	Пентистерический антиусеченный 6-кубовый Терицеллигреаторрогомбатированный гексагонакт (токагракс)					80640	23040
96		т _0,1,2,3,5 {4,3,3,3,3}	Пентирунцикантиусеченный 6-кубовый Теригреатопризматизированный гексагон (tagpox)					80640	23040
97		т _0,1,2,3,4 {4,3,3,3,3}	Стерирунцикантитрированный 6-кубовый Большой ячеистый гексагон (гокакс)					69120	23040
98		т _0,1,2,3,4,5 {4,3,3,3,3}	Усеченный 6-кубовый Большой тери-гексерактигексаконтитетрапетон (готаксог)					138240	46080

Д₆семья

Семейство D ₆ имеет симметрию порядка 23040 (6 факториал x 2 ⁵ ).

Это семейство имеет 3×16−1=47 однородных многогранников Витхоффа, сгенерированных путем маркировки одного или нескольких узлов диаграммы Коксетера-Дынкина D ₆ . Из них 31 (2×16−1) повторяются из семейства B ₆ и 16 являются уникальными для этого семейства. 16 уникальных форм перечислены ниже. Названия акронимов в стиле Боуэрса даны для перекрестных ссылок.

#	Диаграмма Коксетера	Имена	Базовая точка (с альтернативным знаком)	Количество элементов						Circumrad
#	Диаграмма Коксетера	Имена	Базовая точка (с альтернативным знаком)	5	4	3	2	1	0	Circumrad
99	=	6-демикуб Гемигексеракт (hax)	(1,1,1,1,1,1)	44	252	640	640	240	32	0,8660254
100	=	Кантик 6-кубовый усеченный гемигексагон (thax)	(1,1,3,3,3,3)	76	636	2080	3200	2160	480	2.1794493
101	=	Runcic 6-cube Малый ромбовидный полугексагон (сирхакс)	(1,1,1,3,3,3)					3840	640	1.9364916
102	=	Стерический 6-кубовый Малый призматический полугексагексацикл (софакс)	(1,1,1,1,3,3)					3360	480	1.6583123
103	=	Пентик 6-кубовый Мелкоячеистый полугексагексадекс (sochax)	(1,1,1,1,1,3)					1440	192	1.3228756
104	=	Рунцикантик 6-кубовый Большой ромбовидный полугексагексагон (гирхакс)	(1,1,3,5,5,5)					5760	1920	3.2787192
105	=	Стерикантический 6-кубовый призматоусеченный гемигексацикл (питакс)	(1,1,3,3,5,5)					12960	2880	2.95804
106	=	Стерирунцик 6-кубовый призматический ромбовидный гемигексацикл (прохакс)	(1,1,1,3,5,5)					7680	1920	2.7838821
107	=	Пентикантик 6-кубовый Целлитусукцентный гемигексацикл (катикс)	(1,1,3,3,3,5)					9600	1920	2.5980761
108	=	Пентирунцик 6-кубовый целлиромбированный гемигексацикл (крохакс)	(1,1,1,3,3,5)					10560	1920	2.3979158
109	=	Пентистерический 6-кубовый целлипризматический гемихексеракт (кофикс)	(1,1,1,1,3,5)					5280	960	2.1794496
110	=	Стерирунцикантический 6-кубовый Большой призматический гемигексагексацит (гофакс)	(1,1,3,5,7,7)					17280	5760	4.0926762
111	=	Пентирунцикантический 6-кубовый целлигреаторгомбированный гемигексеракт (кагрохакс)	(1,1,3,5,5,7)					20160	5760	3.7080991
112	=	Пентистерический 6-кубовый целлипризматоусеченный гемигексацикл (каптик)	(1,1,3,3,5,7)					23040	5760	3.4278274
113	=	Пентистерирунический 6-кубовый целлипризматоргомбированный гемигексаэкстрак (капрохакс)	(1,1,1,3,5,7)					15360	3840	3.2787192
114	=	Пентистерирунцикантик 6-кубовый Большой ячеистый гемигексагексацит (гохакс)	(1,1,3,5,7,9)					34560	11520	4.5552168

Буква Е₆семья

Существует 39 форм, основанных на всех перестановках диаграмм Коксетера-Дынкина с одним или несколькими кольцами. Для перекрестных ссылок даны аббревиатуры в стиле Боуэрса. Семейство E ₆ имеет симметрию порядка 51 840.

#	Диаграмма Коксетера	Имена	Количество элементов
#	Диаграмма Коксетера	Имена	5-гранный	4-х гранный	Клетки	Лица	Края	Вершины
115		2 ₂₁ Икосихептагептаконтидипетон (як)	99	648	1080	720	216	27
116		Ректифицированный 2 ₂₁ Ректифицированный икосигептагептаконтидипетон (роджак)	126	1350	4320	5040	2160	216
117		Усеченный 2 ₂₁ Усеченный икосигептагептаконтидипетон (тоджак)	126	1350	4320	5040	2376	432
118		Кантеллированный 221 Малый ромбовидный икосигептагептаконтидипетон (сирджак)	342	3942	15120	24480	15120	2160
119		Ранцинированный 221 Мелкий демипризматический икосихептагептаконтидипетон (шопжак)	342	4662	16200	19440	8640	1080
120		Демифицированный икосигептагептаконтидипетон (хеджак)	342	2430	7200	7920	3240	432
121		Усеченный бит 221 Усеченный бит икосигептагептаконтидипетон (ботаджик)						2160
122		Демиректифицированный икосихептагептаконтидипетон (харджак)						1080
123		Кантитруцированный 221 Большой ромбический икосигептагептаконтидипетон (гирьяк)						4320
124		Ранцитусеченный 221 Демипризматоусеченный икосихептагептаконтидипетон (хопитжак)						4320
125		Стериусеченный 221 Целлиусеченный икосигептагептаконтидипетон (catjak)						2160
126		Усеченный икосигептаконтидипетон (хотжак)						2160
127		Runcicantellated 221 Демипризматрохромбированный икосигептагептаконтидипетон (гапрояк)						6480
128		Малый демиромбатированный икосихептагептаконтидипетон (шорджак)						4320
129		Маленький призматический икосигептаконтидипетон (спояк)						4320
130		Трехусеченный икосихептагептаконтидипетон (титаджак)						4320
131		Runcicantiturcated 221 Большой демипризматический икосигептаконтидипетон (ghopjak)						12960
132		Stericantiturcated 221 Celligeratorhombated icosiheptaheptacontidipeton (cograjik)						12960
133		Большой демиромбатированный икосихептахептаконтидипетон (горджак)						8640
134		Икосигептаконтидипетон призматоусеченный (потяк)						12960
135		Демицеллоусеченный икосигептагептаконтидипетон (хиктиджик)						8640
136		Призматорогомбатный икосигептагептаконтидипетон (прояк)						12960
137		Большой призматический икосигептаконтидипетон (гапьяк)						25920
138		Demicelligreatorhombated icosiheptaheptacontidipeton (hocgarjik)						25920

#	Диаграмма Коксетера	Имена	Количество элементов
#	Диаграмма Коксетера	Имена	5-гранный	4-х гранный	Клетки	Лица	Края	Вершины
139	=	1 ₂₂ Пентаконтатетрапетон (мо)	54	702	2160	2160	720	72
140	=	Ректифицированный 1 ₂₂ Ректифицированный пентаконтатетрапетон (рам)	126	1566	6480	10800	6480	720
141	=	Биректифицированный 1 ₂₂ Биректифицированный пентаконтатетрапетон (БМ)	126	2286	10800	19440	12960	2160
142	=	Триректифицированный 122 Триректифицированный пентаконтатетрапетон (обрезка)	558	4608	8640	6480	2160	270
143	=	Усеченный 1 ₂₂ Усеченный пентаконтатетрапетон (тим)					13680	1440
144	=	Бит-усеченный 122 Бит-усеченный пентаконтатетрапетон (битем)						6480
145	=	Триутсеченный 122 Триутсеченный пентаконтатетрапетон (титам)						8640
146	=	Кантеллированный 122 Малый ромбовидный пентаконтатетрапетон (sram)						6480
147	=	Кантитруцированный 122 Большой ромбический пентаконтатетрапетон (грамм)						12960
148	=	Runcinated 122 Маленький призматический пентаконтатетрапетон (спам)						2160
149	=	Двояковыпуклый 122 Малый биромбатный пентаконтатетрапетон (сабрим)						6480
150	=	Бикантиусечённый 122 Большой биромбатный пентаконтатетрапетон (габрим)						12960
151	=	Runciturcated 122 Призмато-усеченный пентаконтатетрапетон (патом)						12960
152	=	Runcicantellated 122 Призматрономбатированный пентаконтатетрапетон (выпускной)						25920
153	=	Всеусеченный 122 Большой призматический пентаконтатетрапетон (гопам)						51840

Триапризмы

Однородные трипризмы , { p }×{ q }×{ r }, образуют бесконечный класс для всех целых чисел p , q , r >2. {4}×{4}×{4} образует форму с более низкой симметрией 6-куба .

Расширенный f-вектор равен ( p , p , 1 )*( q , q , 1 )*( r , r , 1 )=( pqr ,3 pqr ,3 pqr + pq + pr + qr ,3 p ( p +1),3 p , 1 ).

Диаграмма Коксетера	Имена	Количество элементов
Диаграмма Коксетера	Имена	5-гранный	4-х гранный	Клетки	Лица	Края	Вершины
	{ п }×{ д }×{ г } ^[4]	п + д + р	pq + pr + qr + p + q + r	pqr +2( pq + pr + qr )	3 пкв + пкв + пр + кв	3 пквр	пкр
	{ п }×{ п }×{ п }	3 п.	3 п ( п +1)	стр ² ( стр +6)	3 п ² ( п +1)	3 стр ³	стр ³
	{3}×{3}×{3} (триттип)	9	36	81	99	81	27
	{4}×{4}×{4} = 6-куб	12	60	160	240	192	64

Невитхоффовы 6-мерные многогранники

В 6 измерениях и выше существует бесконечное количество невитхоффовых выпуклых однородных многогранников : декартово произведение большой антипризмы в 4 измерениях и любого правильного многоугольника в 2 измерениях. Пока не доказано, есть ли еще такие многогранники.

Регулярные и однородные соты

Соответствия диаграмм Коксетера-Дынкина между семействами и более высокая симметрия внутри диаграмм. Узлы одного цвета в каждой строке представляют идентичные зеркала. Черные узлы не активны в соответствии.

Существует четыре фундаментальные аффинные группы Коксетера и 27 призматических групп, которые генерируют регулярные и равномерные замощения в 5-мерном пространстве:

#	Группа Коксетера		Формы
1	${\тильда {A}}_{5}$	[3 ^[6] ]	12
2	${\тильда {C}}_{5}$	[4,3 ³ ,4]	35
3	${\тильда {B}}_{5}$	[4,3,3 ^1,1 ] [4,3 ³ ,4,1 ⁺ ]	47 (16 новых)
4	${\tilde {D}}_{5}$	[3 ^1,1 ,3,3 ^1,1 ] [1 ⁺ ,4,3 ³ ,4,1 ⁺ ]	20 (3 новых)

К регулярным и однородным сотам относятся:

${\тильда {A}}_{5}$ Существует 12 уникальных однородных сот, в том числе:
${\тильда {C}}_{5}$ Имеется 35 однородных сот, в том числе:
- Правильные гиперкубические соты евклидова 5-пространства, 5-кубические соты , с символами {4,3 ³ ,4},=
${\тильда {B}}_{5}$ Имеется 47 однородных сот, 16 новых, в том числе:
- Равномерные чередующиеся гиперкубические соты , 5-демикубические соты , с символами h{4,3 ³ ,4},==
${\tilde {D}}_{5}$ , [3 ^1,1 ,3,3 ^1,1 ]: Существует 20 уникальных кольцевых перестановок и 3 новых. Коксетер называет первую из них четвертью 5-кубических сот с символами q{4,3 ³ ,4},=. Другие два новых - это=,=.

Призматические группы
#	Группа Коксетера
1	${\тильда {А}}_{4}$ х ${\tilde {I}}_{1}$	[3 ^[5] ,2,∞]
2	${\тильда {B}}_{4}$ х ${\tilde {I}}_{1}$	[4,3,3 ^1,1 ,2,∞]
3	${\тильда {C}}_{4}$ х ${\tilde {I}}_{1}$	[4,3,3,4,2,∞]
4	${\tilde {D}}_{4}$ х ${\tilde {I}}_{1}$	[3 ^1,1,1,1 ,2,∞]
5	${\tilde {F}}_{4}$ х ${\tilde {I}}_{1}$	[3,4,3,3,2,∞]
6	${\tilde {C}}_{3}$ х х ${\tilde {I}}_{1}$ ${\tilde {I}}_{1}$	[4,3,4,2,∞,2,∞]
7	${\tilde {B}}_{3}$ х х ${\tilde {I}}_{1}$ ${\tilde {I}}_{1}$	[4,3 ^1,1 ,2,∞,2,∞]
8	${\tilde {A}}_{3}$ х х ${\tilde {I}}_{1}$ ${\tilde {I}}_{1}$	[3 ^[4] ,2,∞,2,∞]
9	${\tilde {C}}_{2}$ х х х ${\tilde {I}}_{1}$ ${\tilde {I}}_{1}$ ${\tilde {I}}_{1}$	[4,4,2,∞,2,∞,2,∞]
10	${\tilde {H}}_{2}$ х х х ${\tilde {I}}_{1}$ ${\tilde {I}}_{1}$ ${\tilde {I}}_{1}$	[6,3,2,∞,2,∞,2,∞]
11	${\tilde {A}}_{2}$ х х х ${\tilde {I}}_{1}$ ${\tilde {I}}_{1}$ ${\tilde {I}}_{1}$	[3 ^[3] ,2,∞,2,∞,2,∞]
12	${\tilde {I}}_{1}$ х х х х ${\tilde {I}}_{1}$ ${\tilde {I}}_{1}$ ${\tilde {I}}_{1}$ ${\tilde {I}}_{1}$	[∞,2,∞,2,∞,2,∞,2,∞]
13	${\tilde {A}}_{2}$ х х ${\tilde {A}}_{2}$ ${\tilde {I}}_{1}$	[3 ^[3] ,2,3 ^[3] ,2,∞]
14	${\tilde {A}}_{2}$ х х ${\tilde {B}}_{2}$ ${\tilde {I}}_{1}$	[3 ^[3] ,2,4,4,2,∞]
15	${\tilde {A}}_{2}$ х х ${\tilde {G}}_{2}$ ${\tilde {I}}_{1}$	[3 ^[3] ,2,6,3,2,∞]
16	${\tilde {B}}_{2}$ х х ${\tilde {B}}_{2}$ ${\tilde {I}}_{1}$	[4,4,2,4,4,2,∞]
17	${\tilde {B}}_{2}$ х х ${\tilde {G}}_{2}$ ${\tilde {I}}_{1}$	[4,4,2,6,3,2,∞]
18	${\tilde {G}}_{2}$ х х ${\tilde {G}}_{2}$ ${\tilde {I}}_{1}$	[6,3,2,6,3,2,∞]
19	${\tilde {A}}_{3}$ х ${\tilde {A}}_{2}$	[3 ^[4] ,2,3 ^[3] ]
20	${\tilde {B}}_{3}$ х ${\tilde {A}}_{2}$	[4,3 ^1,1 ,2,3 ^[3] ]
21	${\tilde {C}}_{3}$ х ${\tilde {A}}_{2}$	[4,3,4,2,3 ^[3] ]
22	${\tilde {A}}_{3}$ х ${\tilde {B}}_{2}$	[3 ^[4] ,2,4,4]
23	${\tilde {B}}_{3}$ х ${\tilde {B}}_{2}$	[4,3 ^1,1 ,2,4,4]
24	${\tilde {C}}_{3}$ х ${\tilde {B}}_{2}$	[4,3,4,2,4,4]
25	${\tilde {A}}_{3}$ х ${\tilde {G}}_{2}$	[3 ^[4] ,2,6,3]
26	${\tilde {B}}_{3}$ х ${\tilde {G}}_{2}$	[4,3 ^1,1 ,2,6,3]
27	${\tilde {C}}_{3}$ х ${\tilde {G}}_{2}$	[4,3,4,2,6,3]

Регулярные и однородные гиперболические соты

Не существует компактных гиперболических групп Коксетера ранга 6, групп, которые могут генерировать соты со всеми конечными гранями и конечной вершинной фигурой . Однако существует 12 паракомпактных гиперболических групп Коксетера ранга 6, каждая из которых генерирует однородные соты в 5-мерном пространстве как перестановки колец диаграмм Коксетера.

Гиперболические паракомпактные группы
${\bar {P}}_{5}$ = [3,3 ^[5] ]: ${\widehat {AU}}_{5}$ = [(3,3,3,3,3,4)]: ${\widehat {AR}}_{5}$ = [(3,3,4,3,3,4)]:	${\bar {S}}_{5}$ = [4,3,3 ^2,1 ]: ${\bar {O}}_{5}$ = [3,4,3 ^1,1 ]: ${\bar {N}}_{5}$ = [3,(3,4) ^1,1 ]:	${\bar {U}}_{5}$ = [3,3,3,4,3]: ${\bar {X}}_{5}$ = [3,3,4,3,3]: ${\bar {R}}_{5}$ = [3,4,3,3,4]:	${\bar {Q}}_{5}$ = [3 ^2,1,1,1 ]: ${\bar {M}}_{5}$ = [4,3,3 ^1,1,1 ]: ${\bar {L}}_{5}$ = [3 ^1,1,1,1,1 ]:

Заметки о конструкции Витхоффа для однородных 6-мерных многогранников

Построение отражающих 6-мерных однородных многогранников выполняется с помощью процесса построения Витхоффа и представляется с помощью диаграммы Коксетера-Дынкина , где каждый узел представляет зеркало. Узлы окольцованы, чтобы указать, какие зеркала активны. Полный набор сгенерированных однородных многогранников основан на уникальных перестановках окольцованных узлов. Однородные 6-мерные многогранники названы в соответствии с правильными многогранниками в каждом семействе. Некоторые семейства имеют два правильных конструктора и, таким образом, могут иметь два способа их именования.

Ниже приведены основные операторы, доступные для построения и наименования однородных 6-мерных многогранников.

Призматические формы и бифуркационные графы могут использовать одну и ту же нотацию индексации усечения, но для ясности требуют явной системы нумерации узлов.

Операция	Расширенный символ Шлефли	Описание
Родитель	т ₀ {п, д, р, с, т}	Любой правильный 6-мерный многогранник
Исправлено	т ₁ {п, д, р, с, т}	Ребра полностью усечены до отдельных точек. 6-многогранник теперь имеет объединенные грани родительского и двойственного.
Биректифицированный	т ₂ {п, д, р, с, т}	Биректификация сводит клетки к их двойникам .
Усеченный	т _0,1 {п,д,р,с,т}	Каждая исходная вершина отсекается, а новая грань заполняет пробел. Усечение имеет степень свободы, которая имеет одно решение, создающее однородный усеченный 6-многогранник. 6-многогранник имеет свои исходные грани, удвоенные по сторонам, и содержит грани двойственного.
Усеченный	т _1,2 {п,д,р,с,т}	Бифункция преобразует клетки в их двойное усечение.
Три-усеченный	т _2,3 {п,д,р,с,т}	Три-усечение преобразует 4-грани в их двойное усечение.
Кантеллированный	т _0,2 {п,д,р,с,т}	В дополнение к усечению вершины, каждое исходное ребро скошено, и на их месте появляются новые прямоугольные грани. Равномерная кантеллация находится на полпути между родительской и двойной формами.
Двустворчатый	т _1,3 {п,д,р,с,т}	В дополнение к усечению вершины, каждое исходное ребро скошено, и на их месте появляются новые прямоугольные грани. Равномерная кантеллация находится на полпути между родительской и двойной формами.
Runcinated	т _0,3 {п,д,р,с,т}	В результате выполнения уменьшается количество ячеек и создаются новые ячейки на вершинах и ребрах.
Двуруччатый	т _1,4 {п,д,р,с,т}	В результате выполнения уменьшается количество ячеек и создаются новые ячейки на вершинах и ребрах.
Стерилизованный	т _0,4 {п,д,р,с,т}	Стерификация уменьшает количество 4-граней и создает новые 4-грани в вершинах, на ребрах и на гранях в зазорах.
Пентеллатированный	т _0,5 {п,д,р,с,т}	Пентелляция уменьшает 5-грани и создает новые 5-грани в вершинах, ребрах, гранях и ячейках в зазорах. ( операция расширения для полипета)
Omnitrucated	т _0,1,2,3,4,5 {п,д,р,с,т}	Применяются все пять операторов: усечение, кантелляция, руцинация, стерилизация и пентелляция.

Смотрите также

Список правильных многогранников § Высшие размерности

Примечания

^ Т. Госсет : О правильных и полуправильных фигурах в пространстве n измерений , Вестник математики, Макмиллан, 1900
^ Uniform Polypeta, Джонатан Бауэрс
^ Однородный многогранник
^ "Н,м,к-кончик".

Ссылки

Т. Госсет : О правильных и полуправильных фигурах в пространстве n измерений , Вестник математики , Макмиллан, 1900
А. Буль Стотт : Геометрический вывод полуправильных многогранников из правильных многогранников и пространственного заполнения , Verhandelingen из Koninklijke academy van Wetenschappen, единица ширины Амстердам, Eerste Sectie 11,1, Амстердам, 1910 г.
HSM Коксетер :
- HSM Coxeter, MS Longuet-Higgins и JCP Miller: Однородные многогранники , Philosophical Transactions of the Royal Society of London, Londne, 1954
- HSM Coxeter, Правильные многогранники , 3-е издание, Довер, Нью-Йорк, 1973
Калейдоскопы: избранные труды Х. С. М. Коксетера , под редакцией Ф. Артура Шерка, Питера МакМаллена, Энтони К. Томпсона, Азии Айвик Вайс, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6
- (Документ 22) HSM Coxeter, Правильные и полуправильные многогранники I , [Math. Zeit. 46 (1940) 380-407, MR 2,10]
- (Документ 23) HSM Coxeter, Правильные и полуправильные многогранники II , [Math. Zeit. 188 (1985) 559-591]
- (Документ 24) HSM Coxeter, Правильные и полуправильные многогранники III , [Math. Zeit. 200 (1988) 3-45]
NW Johnson : Теория однородных многогранников и сот , докторская диссертация, Университет Торонто, 1966 г.
Клитцинг, Ричард. «6D однородные многогранники (полипеты)».
Клитцинг, Ричард. «Операторы усечения однородных многогранников».

Внешние ссылки

Имена многогранников
Многогранники различных размерностей, Джонатан Бауэрс
Многомерный глоссарий
Глоссарий гиперпространства, Джордж Ольшевский.

в т е Фундаментальные выпуклые правильные и однородные многогранники в размерностях 2–10
Семья	А _н	Б _н	Я ₂ (п) / Д _н	Е ₆ / Е ₇ / Е ₈ / Ф ₄ / Соль ₂	Н _н
Правильный многоугольник	Треугольник	Квадрат	п-гон	Шестиугольник	Пентагон
Однородный многогранник	Тетраэдр	Октаэдр • Куб	Демикуб		Додекаэдр • Икосаэдр
Равномерный полихорон	Пентахорон	16-ячеечный • Тессеракт	Демитессеракт	24-ячеечный	120-ячеечный • 600-ячеечный
Однородный 5-многогранник	5-симплекс	5-ортоплекс • 5-куб	5-демикуб
Однородный 6-многогранник	6-симплекс	6-ортоплекс • 6-куб	6-демикуб	1 ₂₂ • 2 ₂₁
Однородный 7-многогранник	7-симплекс	7-ортоплекс • 7-куб	7-демикуб	1 ₃₂ • 2 ₃₁ • 3 ₂₁
Однородный 8-многогранник	8-симплекс	8-ортоплекс • 8-куб	8-демикуб	1 ₄₂ • 2 ₄₁ • 4 ₂₁
Однородный 9-многогранник	9-симплекс	9-ортоплекс • 9-куб	9-демикуб
Однородный 10-многогранник	10-симплекс	10-ортоплекс • 10-куб	10-демикуб
Однородный n - многогранник	н - симплекс	n - ортоплекс • n - куб	н - демикуб	1 _к2 • 2 _к1 • к ₂₁	n - пятиугольный многогранник
Темы: Семейства многогранников • Правильный многогранник • Список правильных многогранников и соединений

в т е Фундаментальные выпуклые правильные и однородные соты размерностью 2–9
Космос	Семья	${\tilde {A}}_{n-1}$	${\tilde {C}}_{n-1}$	${\tilde {B}}_{n-1}$	${\tilde {D}}_{n-1}$	${\tilde {G}}_{2}$ / / ${\tilde {F}}_{4}$ ${\tilde {E}}_{n-1}$
Э ²	Равномерная укладка плитки	0 _[3]	δ ₃	hδ ₃	qδ ₃	Шестиугольный
Е ³	Равномерные выпуклые соты	0 _[4]	δ ₄	hδ ₄	qδ ₄
Е ⁴	Равномерный 4-сотовый	0 _[5]	δ ₅	hδ ₅	qδ ₅	24-ячеечные соты
Э ⁵	Равномерный 5-сотовый	0 _[6]	δ ₆	hδ ₆	qδ ₆
Е ⁶	Равномерный 6-сотовый	0 _[7]	δ ₇	hδ ₇	qδ ₇	2 ₂₂
Е ⁷	Равномерный 7-сотовый	0 _[8]	δ ₈	hδ ₈	qδ ₈	1 ₃₃ • 3 ₃₁
Е ⁸	Равномерный 8-сотовый	0 _[9]	δ ₉	hδ ₉	qδ ₉	1 ₅₂ • 2 ₅₁ • 5 ₂₁
Е ⁹	Равномерный 9-сотовый	0 _[10]	δ ₁₀	hδ ₁₀	qδ ₁₀
Е ¹⁰	Равномерный 10-сотовый	0 _[11]	δ ₁₁	hδ ₁₁	qδ ₁₁
Э ^{н -1}	Равномерный ( n -1)- соты	0 _{[ н ]}	δ _н	hδ _n	qδ _n	1 _к2 • 2 _к1 • к ₂₁

[1] Т. Госсет : О правильных и полуправильных фигурах в пространстве n измерений , Вестник математики, Макмиллан, 1900

[2] Uniform Polypeta, Джонатан Бауэрс

[3] Однородный многогранник

[4] "Н,м,к-кончик".