Пентеллированные 6-симплексы
 6-симплекс            |  Пентеллитный 6-симплекс            |  Пятиусеченный 6-симплекс            |  Пятилучевой 6-симплекс            |
 Пентикантитруктурированный 6-симплекс            |  Пентирунцитруцированный 6-симплекс            |  Пентирунцикантеллированный 6-симплекс            |  Пентирунцикантиусеченный 6-симплекс            |
 Пентистеритусеченный 6-симплекс            |  Пентистерический антиусеченный 6-симплекс            |  Пентистерирунцикантиусеченный 6-симплекс (Омнитрункированный 6-симплекс)            | |
| Ортогональные проекции в плоскости Коксетера A6 | |||
|---|---|---|---|
В шестимерной геометрии пентеллированный 6-симплекс — это выпуклый однородный 6-многогранник с усечениями 5-го порядка правильного 6-симплекса .
Существуют уникальные 10 степеней пентелляции 6-симплекса с перестановками усечений, кантелляций, рунцинаций и стерикаций. Простой пентелляционный 6-симплекс также называется расширенным 6-симплексом , построенным с помощью операции расширения, примененной к обычному 6-симплексу . Самая высокая форма, пентистерирунцикантиутрескнутый 6-симплекс , называется всеусеченным 6-симплексом со всеми окольцованными узлами.
Пентеллитный 6-симплекс
| Пентеллитный 6-симплекс | |
|---|---|
| Тип | Однородный 6-многогранник |
| Символ Шлефли | т 0,5 {3,3,3,3,3} |
| Диаграмма Коксетера-Дынкина |            |
| 5-гранный | 126: 7+7 {3 4 }  21+21 {}×{3,3,3} 35+35 {3}×{3,3} |
| 4-х гранный | 434 |
| Клетки | 630 |
| Лица | 490 |
| Края | 210 |
| Вершины | 42 |
| Вершинная фигура | 5-клеточная антипризма |
| Группа Коксетера | A 6 ×2, [[3,3,3,3,3]], заказ 10080 |
| Характеристики | выпуклый |
Альтернативные названия
- Расширенный 6-симплекс
- Малый терированный тетрадекапетон (сокращение: staf) (Джонатан Бауэрс) [1]
Поперечные сечения
Максимальное сечение пентеллированного 6-симплекса с 5-мерной гиперплоскостью — стерический гексатерон . Это сечение делит пентеллированный 6-симплекс на два гексагональных гиперкупола, состоящих из 7 5-симплексов , 21 5-ячеечной призмы и 35 тетраэдрально-треугольных дуопризм каждый.
Координаты
Вершины пентеллированного 6-симплекса могут быть расположены в 7-пространстве как перестановки (0,1,1,1,1,1,2). Эта конструкция основана на гранях пентеллированного 7-ортоплекса .
Вторая конструкция в 7-мерном пространстве из центра выпрямленного 7-ортоплекса задается перестановками координат:
- (1,-1,0,0,0,0,0)
Корневые векторы
Его 42 вершины представляют корневые векторы простой группы Ли A 6 . Это вершинная фигура 6-симплексных сот .
Изображения
| Самолет Коксетера | А 6 | А 5 | А 4 |
|---|---|---|---|
| График |  |  |  |
| Симметрия | [[7]] (*) =[14] | [6] | [[5]] (*) =[10] |
| Самолет Коксетера | А 3 | А 2 | |
| График |  |  | |
| Симметрия | [4] | [[3]] (*) =[6] |
- Примечание: (*) Симметрия удваивается для графов A k с четным k из-за симметрично-кольцевой диаграммы Коксетера-Дынкина.
Конфигурация
Эта матрица конфигурации представляет собой расширенный 6-симплекс с 12 перестановками элементов. Строки и столбцы соответствуют вершинам, ребрам, граням, ячейкам, 4-граням и 5-граням. Диагональные числа говорят, сколько элементов каждого элемента встречается во всем многограннике. Недиагональные числа говорят, сколько элементов столбца встречается в элементе строки или рядом с ним. [2]
| Элемент | ф к | ф 0 | ф 1 | ф 2 | ф 3 | ф 4 | ф 5 | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
           | ф 0 | 42 | 10 | 20 | 20 | 20 | 60 | 10 | 40 | 30 | 2 | 10 | 20 |
             | ф 1 | 2 | 210 | 4 | 4 | 6 | 18 | 4 | 16 | 12 | 1 | 5 | 10 |
             | ф 2 | 3 | 3 | 280 | * | 3 | 3 | 3 | 6 | 3 | 1 | 3 | 4 |
           | 4 | 4 | * | 210 | 0 | 6 | 0 | 6 | 6 | 0 | 2 | 6 | |
             | ф 3 | 4 | 6 | 4 | 0 | 210 | * | 2 | 2 | 0 | 1 | 2 | 1 |
             | 6 | 9 | 2 | 3 | * | 420 | 0 | 2 | 2 | 0 | 1 | 3 | |
             | ф 4 | 5 | 10 | 10 | 0 | 5 | 0 | 84 | * | * | 1 | 1 | 0 |
             | 8 | 16 | 8 | 6 | 2 | 4 | * | 210 | * | 0 | 1 | 1 | |
           | 9 | 18 | 6 | 9 | 0 | 6 | * | * | 140 | 0 | 0 | 2 | |
             | ф 5 | 6 | 15 | 20 | 0 | 15 | 0 | 6 | 0 | 0 | 14 | * | * |
             | 10 | 25 | 20 | 10 | 10 | 10 | 2 | 5 | 0 | * | 42 | * | |
             | 12 | 30 | 16 | 18 | 3 | 18 | 0 | 3 | 4 | * | * | 70 | |
Пятиусеченный 6-симплекс
| Пятиусеченный 6-симплекс | |
|---|---|
| Тип | однородный 6-многогранник |
| Символ Шлефли | т 0,1,5 {3,3,3,3,3} |
| Диаграммы Коксетера-Дынкина |            |
| 5-гранный | 126 |
| 4-х гранный | 826 |
| Клетки | 1785 |
| Лица | 1820 |
| Края | 945 |
| Вершины | 210 |
| Вершинная фигура | |
| Группа Коксетера | А 6 , [3,3,3,3,3], заказ 5040 |
| Характеристики | выпуклый |
Альтернативные названия
- Теракеллированный гептапетон (сокращение: токал) (Джонатан Бауэрс) [3]
Координаты
Вершины усеченного 6-симплекса проще всего расположить в 7-пространстве как перестановки (0,1,1,1,1,2,3). Эта конструкция основана на гранях усеченного 7-ортоплекса .
Изображения
| Самолет Коксетера | А 6 | А 5 | А 4 |
|---|---|---|---|
| График |  |  |  |
| Диэдральная симметрия | [7] | [6] | [5] |
| Самолет Коксетера | А 3 | А 2 | |
| График |  |  | |
| Диэдральная симметрия | [4] | [3] |
Пятилучевой 6-симплекс
| Пятилучевой 6-симплекс | |
|---|---|
| Тип | однородный 6-многогранник |
| Символ Шлефли | т 0,2,5 {3,3,3,3,3} |
| Диаграммы Коксетера-Дынкина |            |
| 5-гранный | 126 |
| 4-х гранный | 1246 |
| Клетки | 3570 |
| Лица | 4340 |
| Края | 2310 |
| Вершины | 420 |
| Вершинная фигура | |
| Группа Коксетера | А 6 , [3,3,3,3,3], заказ 5040 |
| Характеристики | выпуклый |
Альтернативные названия
- Терипризматизированный гептапетон (сокращение: топал) (Джонатан Бауэрс) [4]
Координаты
Вершины рантикантеллированного 6-симплекса проще всего расположить в 7-пространстве как перестановки (0,1,1,1,1,2,3). Эта конструкция основана на гранях пентикантеллированного 7-ортоплекса .
Изображения
| Самолет Коксетера | А 6 | А 5 | А 4 |
|---|---|---|---|
| График |  |  |  |
| Диэдральная симметрия | [7] | [6] | [5] |
| Самолет Коксетера | А 3 | А 2 | |
| График |  |  | |
| Диэдральная симметрия | [4] | [3] |
Пентикантитруктурированный 6-симплекс
| пентикантитруктурированный 6-симплекс | |
|---|---|
| Тип | однородный 6-многогранник |
| Символ Шлефли | т 0,1,2,5 {3,3,3,3,3} |
| Диаграммы Коксетера-Дынкина |            |
| 5-гранный | 126 |
| 4-х гранный | 1351 |
| Клетки | 4095 |
| Лица | 5390 |
| Края | 3360 |
| Вершины | 840 |
| Вершинная фигура | |
| Группа Коксетера | А 6 , [3,3,3,3,3], заказ 5040 |
| Характеристики | выпуклый |
Альтернативные названия
- Terigreatorhombated heptapeton (Акроним: togral) (Джонатан Бауэрс) [5]
Координаты
Вершины пентикантиусеченного 6-симплекса проще всего расположить в 7-пространстве как перестановки (0,1,1,1,2,3,4). Эта конструкция основана на гранях пентикантиусеченного 7-ортоплекса .
Изображения
| Самолет Коксетера | А 6 | А 5 | А 4 |
|---|---|---|---|
| График |  |  |  |
| Диэдральная симметрия | [7] | [6] | [5] |
| Самолет Коксетера | А 3 | А 2 | |
| График |  |  | |
| Диэдральная симметрия | [4] | [3] |
Пентирунцитруцированный 6-симплекс
| пентирунцитруцированный 6-симплекс | |
|---|---|
| Тип | однородный 6-многогранник |
| Символ Шлефли | т 0,1,3,5 {3,3,3,3,3} |
| Диаграммы Коксетера-Дынкина |            |
| 5-гранный | 126 |
| 4-х гранный | 1491 |
| Клетки | 5565 |
| Лица | 8610 |
| Края | 5670 |
| Вершины | 1260 |
| Вершинная фигура | |
| Группа Коксетера | А 6 , [3,3,3,3,3], заказ 5040 |
| Характеристики | выпуклый |
Альтернативные названия
- Терицеллиромбатированный гептапетон (сокращение: tocral) (Джонатан Бауэрс) [6]
Координаты
Вершины пятиконечноусеченного 6-симплекса проще всего расположить в 7-пространстве как перестановки (0,1,1,1,2,3,4). Эта конструкция основана на гранях пятиконечноусеченного 7-ортоплекса .
Изображения
| Самолет Коксетера | А 6 | А 5 | А 4 |
|---|---|---|---|
| График |  |  |  |
| Диэдральная симметрия | [7] | [6] | [5] |
| Самолет Коксетера | А 3 | А 2 | |
| График |  |  | |
| Диэдральная симметрия | [4] | [3] |
Пентирунцикантеллированный 6-симплекс
| Пентирунцикантеллированный 6-симплекс | |
|---|---|
| Тип | однородный 6-многогранник |
| Символ Шлефли | т 0,2,3,5 {3,3,3,3,3} |
| Диаграммы Коксетера-Дынкина |            |
| 5-гранный | 126 |
| 4-х гранный | 1596 |
| Клетки | 5250 |
| Лица | 7560 |
| Края | 5040 |
| Вершины | 1260 |
| Вершинная фигура | |
| Группа Коксетера | А 6 , [[3,3,3,3,3]], заказ 10080 |
| Характеристики | выпуклый |
Альтернативные названия
- Терипризматоромбатированный тетрадекапетон (Акроним: тапорф) (Джонатан Бауэрс) [7]
Координаты
Вершины пентирунцикантеллированного 6-симплекса могут быть наиболее просто расположены в 7-пространстве как перестановки (0,1,1,2,3,3,4). Эта конструкция основана на гранях пентирунцикантеллированного 7-ортоплекса .
Изображения
| Самолет Коксетера | А 6 | А 5 | А 4 |
|---|---|---|---|
| График |  |  |  |
| Симметрия | [[7]] (*) =[14] | [6] | [[5]] (*) =[10] |
| Самолет Коксетера | А 3 | А 2 | |
| График |  |  | |
| Симметрия | [4] | [[3]] (*) =[6] |
- Примечание: (*) Симметрия удваивается для графов A k с четным k из-за симметрично-кольцевой диаграммы Коксетера-Дынкина.
Пентирунцикантиусеченный 6-симплекс
| Пентирунцикантиусеченный 6-симплекс | |
|---|---|
| Тип | однородный 6-многогранник |
| Символ Шлефли | т 0,1,2,3,5 {3,3,3,3,3} |
| Диаграммы Коксетера-Дынкина |            |
| 5-гранный | 126 |
| 4-х гранный | 1701 |
| Клетки | 6825 |
| Лица | 11550 |
| Края | 8820 |
| Вершины | 2520 |
| Вершинная фигура | |
| Группа Коксетера | А 6 , [3,3,3,3,3], заказ 5040 |
| Характеристики | выпуклый |
Альтернативные названия
- Теригреопризматический гептапетон (Акроним: тагопал) (Джонатан Бауэрс) [8]
Координаты
Вершины пентирунцикантиусеченного 6-симплекса проще всего расположить в 7-пространстве как перестановки (0,1,1,2,3,4,5). Эта конструкция основана на гранях пентирунцикантиусеченного 7-ортоплекса .
Изображения
| Самолет Коксетера | А 6 | А 5 | А 4 |
|---|---|---|---|
| График |  |  |  |
| Диэдральная симметрия | [7] | [6] | [5] |
| Самолет Коксетера | А 3 | А 2 | |
| График |  |  | |
| Диэдральная симметрия | [4] | [3] |
Пентистеритусеченный 6-симплекс
| Пентистеритусеченный 6-симплекс | |
|---|---|
| Тип | однородный 6-многогранник |
| Символ Шлефли | т 0,1,4,5 {3,3,3,3,3} |
| Диаграммы Коксетера-Дынкина |            |
| 5-гранный | 126 |
| 4-х гранный | 1176 |
| Клетки | 3780 |
| Лица | 5250 |
| Края | 3360 |
| Вершины | 840 |
| Вершинная фигура | |
| Группа Коксетера | А 6 , [[3,3,3,3,3]], заказ 10080 |
| Характеристики | выпуклый |
Альтернативные названия
- Терицеллиусеченный тетрадекапетон (Акроним: тактаф) (Джонатан Бауэрс) [9]
Координаты
Вершины пентистериусеченного 6-симплекса проще всего расположить в 7-пространстве как перестановки (0,1,2,2,2,3,4). Эта конструкция основана на гранях пентистериусеченного 7-ортоплекса .
Изображения
| Самолет Коксетера | А 6 | А 5 | А 4 |
|---|---|---|---|
| График |  |  |  |
| Симметрия | [[7]] (*) =[14] | [6] | [[5]] (*) =[10] |
| Самолет Коксетера | А 3 | А 2 | |
| График |  |  | |
| Симметрия | [4] | [[3]] (*) =[6] |
- Примечание: (*) Симметрия удваивается для графов A k с четным k из-за симметрично-кольцевой диаграммы Коксетера-Дынкина.
Пентистерический антиусеченный 6-симплекс
| пентистерическийантитруктурированный 6-симплекс | |
|---|---|
| Тип | однородный 6-многогранник |
| Символ Шлефли | т 0,1,2,4,5 {3,3,3,3,3} |
| Диаграммы Коксетера-Дынкина |            |
| 5-гранный | 126 |
| 4-х гранный | 1596 |
| Клетки | 6510 |
| Лица | 11340 |
| Края | 8820 |
| Вершины | 2520 |
| Вершинная фигура | |
| Группа Коксетера | А 6 , [3,3,3,3,3], заказ 5040 |
| Характеристики | выпуклый |
Альтернативные названия
- Большой терацеллиромбатный гептапетон (сокращение: gatocral) (Джонатан Бауэрс) [10]
Координаты
Вершины пентистерического антиусеченного 6-симплекса проще всего расположить в 7-пространстве как перестановки (0,1,2,2,3,4,5). Эта конструкция основана на гранях пентистерического антиусеченного 7-ортоплекса .
Изображения
| Самолет Коксетера | А 6 | А 5 | А 4 |
|---|---|---|---|
| График |  |  |  |
| Диэдральная симметрия | [7] | [6] | [5] |
| Самолет Коксетера | А 3 | А 2 | |
| График |  |  | |
| Диэдральная симметрия | [4] | [3] |
Усеченный 6-симплекс
| Усеченный 6-симплекс | |
|---|---|
| Тип | Однородный 6-многогранник |
| Символ Шлефли | т 0,1,2,3,4,5 {3 5 } |
| Диаграммы Коксетера-Дынкина |            |
| 5-гранный | 126: 14 т 0,1,2,3,4 {3 4 }  42 {}×t 0,1,2,3 {3 3 }  × × 70 {6}×t 0,1,2 {3,3}  × × |
| 4-х гранный | 1806 |
| Клетки | 8400 |
| Лица | 16800: 4200 {6}  1260 {4}  |
| Края | 15120 |
| Вершины | 5040 |
| Вершинная фигура | 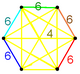 нерегулярный 5-симплекс |
| Группа Коксетера | А 6 , [[3 5 ]], заказ 10080 |
| Характеристики | выпуклый , изогональный , зонотоп |
Всеусеченный 6-симплекс имеет 5040 вершин , 15120 ребер , 16800 граней (4200 шестиугольников и 1260 квадратов ), 8400 ячеек , 1806 4-граней и 126 5-граней. С 5040 вершинами он является крупнейшим из 35 однородных 6-многогранников, полученных из правильного 6-симплекса .
Альтернативные названия
- Пентистерирунцикантиусеченный 6-симплекс ( униторка Джонсона для 6-многогранников)
- Усеченный гептапетон
- Большой тератированный тетрадекапетон (Акроним: gotaf) (Джонатан Бауэрс) [11]
Пермутоэдр и связанная с ним тесселяция
Всеусеченный 6-симплекс является пермутоэдром порядка 7. Всеусеченный 6-симплекс является зонотопом , суммой Минковского семи отрезков прямых, параллельных семи прямым, проходящим через начало координат и семь вершин 6-симплекса.
Как и все равномерные всеусеченные n-симплексы, всеусеченный 6-симплекс может сам по себе замощать пространство, в данном случае 6-мерное пространство с тремя гранями вокруг каждой гиперячейки. Он имеет диаграмму Коксетера-Дынкина





 .
.
Координаты
Вершины всеусеченного 6-симплекса могут быть наиболее просто расположены в 7-пространстве как перестановки (0,1,2,3,4,5,6). Эта конструкция основана на гранях пентистерирунцикантиусеченного 7-ортоплекса , t 0,1,2,3,4,5 {3 5 ,4},











 .
.
Изображения
| Самолет Коксетера | А 6 | А 5 | А 4 |
|---|---|---|---|
| График |  |  |  |
| Симметрия | [[7]] (*) =[14] | [6] | [[5]] (*) =[10] |
| Самолет Коксетера | А 3 | А 2 | |
| График |  | 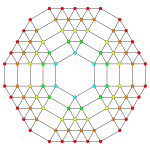 | |
| Симметрия | [4] | [[3]] (*) =[6] |
- Примечание: (*) Симметрия удваивается для графов A k с четным k из-за симметрично-кольцевой диаграммы Коксетера-Дынкина.
Конфигурация
Эта матрица конфигурации представляет собой всеусеченный 6-симплекс с 35 перестановками элементов. Строки и столбцы соответствуют вершинам, ребрам, граням, ячейкам, 4-граням и 5-граням. Диагональные числа говорят, сколько элементов каждого элемента встречается во всем многограннике. Недиагональные числа говорят, сколько элементов столбца встречается в элементе строки или рядом с ним. [12]
| Элемент | ф к | ф 0 | ф 1 | ф 2 | ф 3 | ф 4 | ф 5 | |||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
           | ф 0 | 5040 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 1 | 2 | 2 | 1 | 1 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 1 | 2 | 1 | 1 | 2 | 2 | 2 |
             | ф 1 | 2 | 5040 | * | * | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 2 | 1 | 1 | 2 | 1 | 0 | 0 | 1 | 1 | 2 | 1 | 2 | 1 | 1 | 1 | 0 | 1 | 2 | 2 |
             | 2 | * | 5040 | * | 1 | 0 | 0 | 1 | 0 | 1 | 1 | 1 | 0 | 1 | 1 | 2 | 1 | 0 | 1 | 0 | 1 | 1 | 2 | 1 | 2 | 1 | 2 | 1 | 1 | 1 | 0 | 1 | 2 | 1 | 2 | |
             | 2 | * | * | 5040 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 2 | 1 | 1 | 1 | 2 | 1 | 2 | 1 | 1 | 1 | 1 | 0 | 2 | 1 | 1 | 2 | 2 | 1 | |
             | ф 2 | 6 | 3 | 3 | 0 | 1680 | * | * | * | * | * | * | * | * | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 2 |
             | 4 | 2 | 0 | 2 | * | 2520 | * | * | * | * | * | * | * | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 1 | 0 | 1 | 1 | 0 | 1 | 2 | 1 | |
             | 4 | 2 | 0 | 2 | * | * | 2520 | * | * | * | * | * | * | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 1 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | 2 | 1 | |
             | 4 | 2 | 2 | 0 | * | * | * | 2520 | * | * | * | * | * | 0 | 0 | 1 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 2 | |
           | 4 | 4 | 0 | 0 | * | * | * | * | 1260 | * | * | * | * | 0 | 0 | 0 | 2 | 0 | 0 | 2 | 0 | 0 | 0 | 0 | 0 | 2 | 0 | 2 | 1 | 0 | 1 | 0 | 0 | 2 | 2 | |
             | 6 | 0 | 3 | 3 | * | * | * | * | * | 1680 | * | * | * | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 1 | 0 | 1 | 2 | 1 | 1 | |
             | 4 | 0 | 2 | 2 | * | * | * | * | * | * | 2520 | * | * | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | 0 | 1 | 2 | 1 | 1 | |
           | 4 | 0 | 4 | 0 | * | * | * | * | * | * | * | 1260 | * | 0 | 0 | 2 | 0 | 0 | 0 | 0 | 0 | 0 | 2 | 0 | 2 | 0 | 2 | 0 | 1 | 0 | 0 | 1 | 2 | 0 | 2 | |
           | 6 | 0 | 0 | 6 | * | * | * | * | * | * | * | * | 840 | 0 | 0 | 0 | 0 | 2 | 0 | 0 | 0 | 2 | 0 | 2 | 0 | 0 | 0 | 0 | 0 | 2 | 1 | 1 | 2 | 2 | 0 | |
             | ф 3 | 24 | 12 | 12 | 12 | 4 | 6 | 0 | 0 | 0 | 4 | 0 | 0 | 0 | 420 | * | * | * | * | * | * | * | * | * | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 |
             | 12 | 6 | 6 | 6 | 2 | 0 | 3 | 0 | 0 | 0 | 3 | 0 | 0 | * | 840 | * | * | * | * | * | * | * | * | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | |
             | 12 | 6 | 12 | 0 | 2 | 0 | 0 | 3 | 0 | 0 | 0 | 3 | 0 | * | * | 840 | * | * | * | * | * | * | * | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 2 | |
             | 12 | 12 | 6 | 0 | 2 | 0 | 0 | 3 | 3 | 0 | 0 | 0 | 0 | * | * | * | 840 | * | * | * | * | * | * | 0 | 0 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 2 | |
             | 12 | 6 | 0 | 12 | 0 | 3 | 3 | 0 | 0 | 0 | 0 | 0 | 2 | * | * | * | * | 840 | * | * | * | * | * | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 1 | 2 | 0 | |
             | 8 | 4 | 4 | 4 | 0 | 2 | 0 | 2 | 0 | 0 | 2 | 0 | 0 | * | * | * | * | * | 1260 | * | * | * | * | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 1 | 1 | 1 | |
             | 8 | 8 | 0 | 4 | 0 | 2 | 2 | 0 | 2 | 0 | 0 | 0 | 0 | * | * | * | * | * | * | 1260 | * | * | * | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 2 | 1 | |
             | 12 | 6 | 6 | 6 | 0 | 0 | 3 | 3 | 0 | 2 | 0 | 0 | 0 | * | * | * | * | * | * | * | 840 | * | * | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 1 | 1 | |
             | 24 | 0 | 12 | 24 | 0 | 0 | 0 | 0 | 0 | 4 | 6 | 0 | 4 | * | * | * | * | * | * | * | * | 420 | * | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 2 | 1 | 0 | |
             | 12 | 0 | 12 | 6 | 0 | 0 | 0 | 0 | 0 | 2 | 3 | 3 | 0 | * | * | * | * | * | * | * | * | * | 840 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 2 | 0 | 1 | |
             | ф 4 | 120 | 60 | 60 | 120 | 20 | 30 | 30 | 0 | 0 | 20 | 30 | 0 | 20 | 5 | 10 | 0 | 0 | 10 | 0 | 0 | 0 | 5 | 0 | 84 | * | * | * | * | * | * | * | * | 1 | 1 | 0 |
             | 48 | 24 | 48 | 24 | 8 | 12 | 0 | 12 | 0 | 8 | 12 | 12 | 0 | 2 | 0 | 4 | 0 | 0 | 6 | 0 | 0 | 0 | 4 | * | 210 | * | * | * | * | * | * | * | 1 | 0 | 1 | |
             | 48 | 48 | 24 | 24 | 8 | 12 | 12 | 12 | 12 | 8 | 0 | 0 | 0 | 2 | 0 | 0 | 4 | 0 | 0 | 6 | 4 | 0 | 0 | * | * | 210 | * | * | * | * | * | * | 0 | 1 | 1 | |
             | 36 | 18 | 36 | 18 | 6 | 0 | 9 | 9 | 0 | 6 | 9 | 9 | 0 | 0 | 3 | 3 | 0 | 0 | 0 | 0 | 3 | 0 | 3 | * | * | * | 280 | * | * | * | * | * | 1 | 0 | 1 | |
             | 24 | 24 | 12 | 12 | 4 | 6 | 6 | 6 | 6 | 0 | 6 | 0 | 0 | 0 | 2 | 0 | 2 | 0 | 3 | 3 | 0 | 0 | 0 | * | * | * | * | 420 | * | * | * | * | 0 | 1 | 1 | |
           | 36 | 36 | 36 | 0 | 12 | 0 | 0 | 18 | 9 | 0 | 0 | 9 | 0 | 0 | 0 | 6 | 6 | 0 | 0 | 0 | 0 | 0 | 0 | * | * | * | * | * | 140 | * | * | * | 0 | 0 | 2 | |
             | 48 | 24 | 24 | 48 | 0 | 12 | 12 | 12 | 0 | 8 | 12 | 0 | 8 | 0 | 0 | 0 | 0 | 4 | 6 | 0 | 4 | 2 | 0 | * | * | * | * | * | * | 210 | * | * | 1 | 1 | 0 | |
           | 24 | 24 | 0 | 24 | 0 | 12 | 12 | 0 | 6 | 0 | 0 | 0 | 4 | 0 | 0 | 0 | 0 | 4 | 0 | 6 | 0 | 0 | 0 | * | * | * | * | * | * | * | 210 | * | 0 | 2 | 0 | |
           | 120 | 0 | 120 | 120 | 0 | 0 | 0 | 0 | 0 | 40 | 60 | 30 | 20 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 10 | 20 | * | * | * | * | * | * | * | * | 42 | 2 | 0 | 0 | |
             | ф 5 | 720 | 360 | 720 | 720 | 120 | 180 | 180 | 180 | 0 | 240 | 360 | 180 | 120 | 30 | 60 | 60 | 0 | 60 | 90 | 0 | 60 | 60 | 120 | 6 | 15 | 0 | 20 | 0 | 0 | 15 | 0 | 6 | 14 | * | * |
             | 240 | 240 | 120 | 240 | 40 | 120 | 120 | 60 | 60 | 40 | 60 | 0 | 40 | 10 | 20 | 0 | 20 | 40 | 30 | 60 | 20 | 10 | 0 | 2 | 0 | 5 | 0 | 10 | 0 | 5 | 10 | 0 | * | 42 | * | |
             | 144 | 144 | 144 | 72 | 48 | 36 | 36 | 72 | 36 | 24 | 36 | 36 | 0 | 6 | 12 | 24 | 24 | 0 | 18 | 18 | 12 | 0 | 12 | 0 | 3 | 3 | 4 | 6 | 4 | 0 | 0 | 0 | * | * | 70 | |
Полный курносый 6-симплекс
Полный плосконосый 6-симплекс или омниплоский 6-симплекс , определяемый как чередование омниусеченного 6-симплекса, не является однородным, но его можно представить в виде диаграммы Коксетера









 и симметрия [[3,3,3,3,3]] + , и построен из 14 плосконосых 5-симплексов , 42 плосконосых 5-ячеистых антипризм, 70 3-s{3,4} дуоантипризм и 2520 неправильных 5-симплексов, заполняющих пробелы в удаленных вершинах.
и симметрия [[3,3,3,3,3]] + , и построен из 14 плосконосых 5-симплексов , 42 плосконосых 5-ячеистых антипризм, 70 3-s{3,4} дуоантипризм и 2520 неправильных 5-симплексов, заполняющих пробелы в удаленных вершинах.
Связанные однородные 6-многогранники
Пятнистый 6-симплекс является одним из 35 однородных 6-мерных многогранников, основанных на группе Коксетера [3,3,3,3,3] , все они показаны здесь в ортографических проекциях Коксетера на плоскость A6 .
Примечания
- ^ Клитцинг, (x3o3o3o3o3x - стаф)
- ^ "Сотрудники".
- ^ Клитцинг, (x3x3o3o3o3x - токальное)
- ^ Клитцинг, (x3o3x3o3o3x - топал)
- ^ Клитцинг, (x3x3x3o3o3x - тограл)
- ^ Клитцинг, (x3x3o3x3o3x - токраль)
- ^ Клитцинг, (x3o3x3x3o3x - taporf)
- ^ Клитцинг, (x3x3x3o3x3x - tagopal)
- ^ Клитцинг, (x3x3o3o3x3x - такт)
- ^ Клитцинг, (x3x3x3o3x3x - гатокрал)
- ^ Клитцинг, (x3x3x3x3x3x - gotaf)
- ^ "Готаф".
Ссылки
- HSM Коксетер :
- HSM Coxeter, Правильные многогранники , 3-е издание, Довер, Нью-Йорк, 1973
- Калейдоскопы: избранные труды Х. С. М. Коксетера , под редакцией Ф. Артура Шерка, Питера МакМаллена, Энтони К. Томпсона, Азии Айвик Вайс, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [1]
- (Документ 22) HSM Coxeter, Правильные и полуправильные многогранники I , [Math. Zeit. 46 (1940) 380-407, MR 2,10]
- (Документ 23) HSM Coxeter, Правильные и полуправильные многогранники II , [Math. Zeit. 188 (1985) 559-591]
- (Документ 24) HSM Coxeter, Правильные и полуправильные многогранники III , [Math. Zeit. 200 (1988) 3-45]
- Норман Джонсон Однородные многогранники , Рукопись (1991)
- Н. В. Джонсон: Теория однородных многогранников и сот , доктор философии.
- Клитцинг, Ричард. «6D однородные многогранники (полипеты)».х3о3о3о3о3х - стаф, х3х3о3о3о3х - токал, х3о3х3о3о3х - топал, х3х3х3о3о3х - тограл, х3х3о3х3о3х - токрал, х3х3х3х3о3х - тагопал, х3х3о3о3х3х - тактаф, x3x3x3o3x3x - такограл, x3x3x3x3x3x - готаф
Внешние ссылки
- Глоссарий гиперпространства, Джордж Ольшевский.
- Многогранники различных размерностей
- Многомерный глоссарий


































