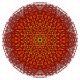
Стерические 6-кубы

6-демикуб
=
Стерический 6-куб
=
Стерикантический 6-кубовый
=

Стерилизующий 6-кубовый
=
Стерикантик 6-кубовый
=
Ортогональные проекции в плоскости Коксетера D 6

В шестимерной геометрии стерический 6-куб — ​​это выпуклый однородный 6-многогранник . Существуют 4 уникальные стерические формы 6-куба.

Стерический 6-куб

Стерический 6-куб
Типоднородный 6-многогранник
Символ Шлефлит 0,3 {3,3 3,1 }
ч 4 {4,3 4 }
Диаграмма Коксетера-Дынкина=
5-гранный
4-х гранный
Клетки
Лица
Края3360
Вершины480
Вершинная фигура
Группы КоксетераД 6 , [3 3,1,1 ]
Характеристикивыпуклый

Альтернативные названия

  • Runcinated demihexeract/6-demicube
  • Малый призматический гемигексацикл (сокращение софакс) (Джонатан Бауэрс) [1]

Декартовы координаты

Декартовы координаты для 480 вершин стерического 6-куба с центром в начале координат представляют собой перестановки координат:

(±1,±1,±1,±1,±1,±3)

с нечетным числом знаков плюс.

Изображения

ортографические проекции
самолет КоксетераБ 6
График
Диэдральная симметрия[12/2]
самолет КоксетераД 6Д 5
График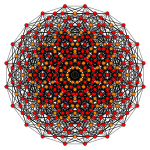
Диэдральная симметрия[10][8]
самолет КоксетераД 4Д 3
График
Диэдральная симметрия[6][4]
самолет КоксетераА 5А 3
График
Диэдральная симметрия[6][4]
Размерное семейство стерических n-кубов
н5678
[1 + ,4,3 n-2 ]
= [3,3 n-3,1 ]		[1 + ,4,3 3 ]
= [3,3 2,1 ]		[1 + ,4,3 4 ]
= [3,3 3,1 ]		[1 + ,4,3 5 ]
= [3,3 4,1 ]		[1 + ,4,3 6 ]
= [3,3 5,1 ]
Стерическая
фигура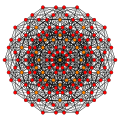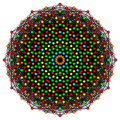
Коксетер
=
=
=
=
Шлефлич 4 {4,3 3 }ч 4 {4,3 4 }ч 4 {4,3 5 }ч 4 {4,3 6 }

Стерикантический 6-кубовый

Стерикантический 6-кубовый
Типоднородный 6-многогранник
Символ Шлефлит 0,1,3 {3,3 3,1 }
ч 2,4 {4,3 4 }
Диаграмма Коксетера-Дынкина=
5-гранный
4-х гранный
Клетки
Лица
Края12960
Вершины2880
Вершинная фигура
Группы КоксетераД 6 , [3 3,1,1 ]
Характеристикивыпуклый

Альтернативные названия

  • Рунцитусеченный полугексеракт/6-демикуб
  • Призматоусеченный гемигексеракт (сокращение питакса) (Джонатан Бауэрс) [2]

Декартовы координаты

Декартовы координаты для 2880 вершин стерекантического 6-куба с центром в начале координат представляют собой перестановки координат:

(±1,±1,±1,±3,±3,±5)

с нечетным числом знаков плюс.

Изображения

ортографические проекции
самолет КоксетераБ 6
График
Диэдральная симметрия[12/2]
самолет КоксетераД 6Д 5
График
Диэдральная симметрия[10][8]
самолет КоксетераД 4Д 3
График
Диэдральная симметрия[6][4]
самолет КоксетераА 5А 3
График
Диэдральная симметрия[6][4]

Стерилизующий 6-кубовый

Стерилизующий 6-кубовый
Типоднородный 6-многогранник
Символ Шлефлит 0,2,3 {3,3 3,1 }
ч 3,4 {4,3 4 }
Диаграмма Коксетера-Дынкина=
5-гранный
4-х гранный
Клетки
Лица
Края7680
Вершины1920
Вершинная фигура
Группы КоксетераД 6 , [3 3,1,1 ]
Характеристикивыпуклый

Альтернативные названия

  • Runcicantellated demihexeract/6-demicube
  • Призматоромбатированный гемигексеракт (сокращение прохакс) (Джонатан Бауэрс) [3]

Декартовы координаты

Декартовы координаты для 1920 вершин стерильного 6-куба с центром в начале координат представляют собой перестановки координат:

(±1,±1,±1,±1,±3,±5)

с нечетным числом знаков плюс.

Изображения

ортографические проекции
самолет КоксетераБ 6
График
Диэдральная симметрия[12/2]
самолет КоксетераД 6Д 5
График
Диэдральная симметрия[10][8]
самолет КоксетераД 4Д 3
График
Диэдральная симметрия[6][4]
самолет КоксетераА 5А 3
График
Диэдральная симметрия[6][4]

Стерилизующий 6-кубовый

Стерилизующий 6-кубовый
Типоднородный 6-многогранник
Символ Шлефлит 0,1,2,3 {3,3 2,1 }
ч 2,3,4 {4,3 4 }
Диаграмма Коксетера-Дынкина=
5-гранный
4-х гранный
Клетки
Лица
Края17280
Вершины5760
Вершинная фигура
Группы КоксетераД 6 , [3 3,1,1 ]
Характеристикивыпуклый

Альтернативные названия

  • Runcicantiусеченный demihexeract/6-demicube
  • Большой призматический гемигексеракт (сокращение гофакс) (Джонатан Бауэрс) [4]

Декартовы координаты

Декартовы координаты для 5760 вершин стерильного 6-куба с центром в начале координат представляют собой перестановки координат:

(±1,±1,±1,±3,±5,±7)

с нечетным числом знаков плюс.

Изображения

ортографические проекции
самолет КоксетераБ 6
График
Диэдральная симметрия[12/2]
самолет КоксетераД 6Д 5
График
Диэдральная симметрия[10][8]
самолет КоксетераД 4Д 3
График
Диэдральная симметрия[6][4]
самолет КоксетераА 5А 3
График
Диэдральная симметрия[6][4]

Существует 47 однородных многогранников с симметрией D6 , 31 из них имеют симметрию B6 , а 16 являются уникальными:

Многогранники D6

ч{4,3 4 }
ч 2 {4,3 4 }
ч 3 {4,3 4 }
ч 4 {4,3 4 }
ч 5 {4,3 4 }
ч 2,3 {4,3 4 }
ч 2,4 {4,3 4 }
ч 2,5 {4,3 4 }

ч 3,4 {4,3 4 }
ч 3,5 {4,3 4 }
ч 4,5 {4,3 4 }
ч 2,3,4 {4,3 4 }
ч 2,3,5 {4,3 4 }
ч 2,4,5 {4,3 4 }
ч 3,4,5 {4,3 4 }
ч 2,3,4,5 {4,3 4 }

Примечания

  1. ^ Клитцинг, (x3o3o *b3o3x3o - софакс)
  2. ^ Клитцинг, (x3x3o *b3o3x3o - питак)
  3. ^ Клитцинг, (x3o3o *b3x3x3o - prohax)
  4. ^ Клитцинг, (x3x3o *b3x3x3o - gophax)

Ссылки

  • HSM Коксетер :
    • HSM Coxeter, Правильные многогранники , 3-е издание, Довер, Нью-Йорк, 1973
    • Калейдоскопы: избранные труды Х. С. М. Коксетера , под редакцией Ф. Артура Шерка, Питера МакМаллена, Энтони К. Томпсона, Азии Айвик Вайс, Wiley-Interscience Publication, 1995, ISBN  978-0-471-01003-6 [1]
      • (Документ 22) HSM Coxeter, Правильные и полуправильные многогранники I , [Math. Zeit. 46 (1940) 380-407, MR 2,10]
      • (Документ 23) HSM Coxeter, Правильные и полуправильные многогранники II , [Math. Zeit. 188 (1985) 559-591]
      • (Документ 24) HSM Coxeter, Правильные и полуправильные многогранники III , [Math. Zeit. 200 (1988) 3-45]
  • Норман Джонсон Однородные многогранники , Рукопись (1991)
    • Н. В. Джонсон: Теория однородных многогранников и сот , доктор философии.
  • Клитцинг, Ричард. «6D однородные многогранники (полипеты)».x3o3o *b3o3x3o - софакс, x3x3o *b3o3x3o - питакс, x3o3o *b3x3x3o - прогакс, x3x3o *b3x3x3o - гофакс
Фундаментальные выпуклые правильные и однородные многогранники в размерностях 2–10
СемьяА нБ нЯ 2 (п) / Д нЕ 6 / Е 7 / Е 8 / Ф 4 / Соль 2Н н
Правильный многоугольникТреугольникКвадратп-гонШестиугольникПентагон
Однородный многогранникТетраэдрОктаэдр • КубДемикубДодекаэдр • Икосаэдр
Равномерный полихоронПентахорон16-ячеечный • ТессерактДемитессеракт24-ячеечный120-ячеечный • 600-ячеечный
Однородный 5-многогранник5-симплекс5-ортоплекс • 5-куб5-демикуб
Однородный 6-многогранник6-симплекс6-ортоплекс • 6-куб6-демикуб1 22 • 2 21
Однородный 7-многогранник7-симплекс7-ортоплекс • 7-куб7-демикуб1 32 • 2 31 • 3 21
Однородный 8-многогранник8-симплекс8-ортоплекс • 8-куб8-демикуб1 42 • 2 41 • 4 21
Однородный 9-многогранник9-симплекс9-ортоплекс • 9-куб9-демикуб
Однородный 10-многогранник10-симплекс10-ортоплекс • 10-куб10-демикуб
Однородный n - многогранникн - симплексn - ортоплекс • n - кубн - демикуб1 к2 • 2 к1 • к 21n - пятиугольный многогранник
Темы: Семейства многогранников • Правильный многогранник • Список правильных многогранников и соединений
Взято с "https://en.wikipedia.org/w/index.php?title=Steric_6-cubes&oldid=1148116639#Steric_6-cube"