2 21 многогранник

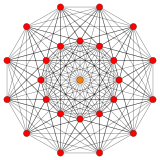ортогональные проекции в плоскости Коксетера E ₆
2 ₂₁	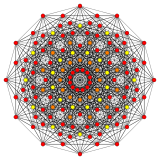Исправлено 2 ₂₁
( 1 ₂₂ )	Двукратно выпрямленный 2 ₂₁ ( Выпрямленный 1 ₂₂ )

В 6-мерной геометрии многогранник 2 ₂₁ является однородным 6-мерным многогранником , построенным в рамках симметрии группы E _6. Он был открыт Торолдом Госсетом и опубликован в его статье 1900 года. Он назвал его 6-мерной полуправильной фигурой . ^[1] Его также называют многогранником Шлефли .

Его символ Коксетера — 2 ₂₁ , описывающий его бифуркационную диаграмму Коксетера-Дынкина с одним кольцом на конце одной из 2-узловых последовательностей. Он также изучал ^[2] его связь с 27 линиями на кубической поверхности , которые естественным образом соответствуют вершинам 2 ₂₁ .

Выпрямленный 2 ₂₁ строится по точкам в средних гранях 2 _21. Двуспрямленный 2 ₂₁ строится по точкам в центрах треугольных граней 2 ₂₁ и совпадает с выпрямленным 1 ₂₂ .

Эти многогранники являются частью семейства из 39 выпуклых однородных многогранников в 6-мерном пространстве , состоящих из однородных граней и вершинных фигур 5-многогранников , определяемых всеми перестановками колец в этой диаграмме Коксетера-Дынкина :.

2_21 многогранник

2 ₂₁ многогранник
Тип	Однородный 6-многогранник
Семья	многогранник k ₂₁
Символ Шлефли	{3,3,3 ^2,1 }
символ Коксетера	2 ₂₁
Диаграмма Коксетера-Дынкина	или
5-гранный	99 всего: 27 2 ₁₁ 72 {3 ⁴ }
4-х гранный	648: 432 {3 ³ } 216 {3 ³ }
Клетки	1080 {3,3}
Лица	720 {3}
Края	216
Вершины	27
Вершинная фигура	1 ₂₁ ( 5-демикуб )
Петри полигон	Двенадцатиугольник
Группа Коксетера	E ₆ , [3 ^2,2,1 ], заказ 51840
Характеристики	выпуклый

2 ₂₁ имеет 27 вершин и 99 граней: 27 5-ортоплексов и 72 5 - симплекса . Его вершинная фигура — 5-демикуб .

Для визуализации этот 6-мерный многогранник часто отображается в специальном наклонном ортографическом направлении проекции, которое вписывает его 27 вершин в 12-угольный правильный многоугольник (называемый многоугольником Петри ). Его 216 ребер нарисованы между 2 кольцами из 12 вершин, и 3 вершины спроецированы в центр. Более высокие элементы (грани, ячейки и т. д.) также могут быть извлечены и нарисованы на этой проекции.

Граф Шлефли является 1-скелетом этого многогранника.

Альтернативные названия

Э. Л. Элте назвал его V ₂₇ (из-за 27 вершин) в своем списке полуправильных многогранников 1912 года. ^[3]
Икосигепта-гептаконтиди-петон - 27-72-гранный полипетон (сокращенно jak) (Джонатан Бауэрс) ^[4]

Координаты

27 вершин можно выразить в 8-мерном пространстве как реберную фигуру многогранника 4 ₂₁ :

(-2, 0, 0, 0,-2, 0, 0, 0),( 0,-2, 0, 0,-2, 0, 0, 0),( 0, 0,-2, 0,-2, 0, 0, 0),( 0, 0, 0,-2,-2, 0, 0, 0),( 0, 0, 0, 0,-2, 0, 0,-2),( 0, 0, 0, 0, 0,-2,-2, 0)

( 2, 0, 0, 0,-2, 0, 0, 0),( 0, 2, 0, 0,-2, 0, 0, 0),( 0, 0, 2, 0,-2, 0, 0, 0),( 0, 0, 0, 2,-2, 0, 0, 0),( 0, 0, 0, 0,-2, 0, 0, 2)

(-1,-1,-1,-1,-1,-1,-1,-1),(-1,-1,-1, 1,-1,-1,-1, 1),(-1,-1, 1,-1,-1,-1,-1, 1),(-1,-1, 1, 1,-1,-1,-1,-1),(-1, 1,-1,-1,-1,-1,-1, 1),(-1, 1,-1, 1,-1,-1,-1,-1),(-1, 1, 1,-1,-1,-1,-1,-1),( 1,-1,-1,-1,-1,-1,-1, 1),( 1,-1, 1,-1,-1,-1,-1,-1),( 1,-1,-1, 1,-1,-1,-1,-1),( 1, 1,-1,-1,-1,-1,-1,-1),(-1, 1, 1, 1,-1,-1,-1,-1, 1),( 1,-1, 1, 1,-1,-1,-1, 1),( 1, 1,-1, 1,-1,-1,-1, 1),( 1, 1, 1,-1,-1,-1,-1, 1),( 1, 1, 1, 1,-1,-1,-1,-1)

Строительство

Его конструкция основана на группе E ₆ .

Информацию о фасетах можно извлечь из диаграммы Коксетера-Дынкина ,.

Удаление узла на короткой ветви оставляет 5-симплекс ,.

Удаление узла на конце ветви длиной 2 оставляет 5-ортоплекс в его измененной форме: ( 2 ₁₁ ),.

Каждая симплексная грань касается 5-ортоплексной грани, в то время как чередующиеся грани ортоплекса касаются либо симплекса, либо другого ортоплекса.

Вершинная фигура определяется путем удаления окольцованного узла и окольцования соседнего узла. Это дает 5-демикуб (1 ₂₁ многогранник),. Реберная фигура является вершинной фигурой вершинной фигуры, выпрямленным 5-ячейником (0 ₂₁ многогранник),.

Рассматривая матрицу конфигурации , количество элементов можно вывести из порядков групп Кокстера . ^[5]

Е ₆	к-лицо	ф _к	ф ₀	ф ₁	ф ₂	ф ₃	ф ₄		ф ₅		к -цифра	примечания
Д ₅	( )	ф ₀	27	16	80	160	80	40	16	10	ч{4,3,3,3}	Э ₆ /Д ₅ = 51840/1920 = 27
А ₄ А ₁	{ }	ф ₁	2	216	10	30	20	10	5	5	г{3,3,3}	Е ₆ /А ₄ А ₁ = 51840/120/2 = 216
А ₂ А ₂ А ₁	{3}	ф ₂	3	3	720	6	6	3	2	3	{3}x{ }	Е ₆ /А ₂ А ₂ А ₁ = 51840/6/6/2 = 720
А ₃ А ₁	{3,3}	ф ₃	4	6	4	1080	2	1	1	2	{ }в( )	Е ₆ /А ₃ А ₁ = 51840/24/2 = 1080
А ₄	{3,3,3}	ф ₄	5	10	10	5	432	*	1	1	{ }	Э ₆ /А ₄ = 51840/120 = 432
А ₄ А ₁	{3,3,3}	ф ₄	5	10	10	5	*	216	0	2	{ }	Е ₆ /А ₄ А ₁ = 51840/120/2 = 216
А ₅	{3,3,3,3}	ф ₅	6	15	20	15	6	0	72	*	( )	Э ₆ /А ₅ = 51840/720 = 72
Д ₅	{3,3,3,4}	ф ₅	10	40	80	80	16	16	*	27	( )	Э ₆ /Д ₅ = 51840/1920 = 27

Изображения

Вершины окрашены в соответствии с их кратностью в этой проекции в прогрессирующем порядке: красный, оранжевый, желтый. Количество вершин по цвету указано в скобках.

Ортографические проекции плоскости Коксетера
Е6 [12]	Д5 [8]	Д4/А2 [6]	Б6 [12/2]
(1,3)	(1,3)	(3,9)	(1,3)
А5 [6]	А4 [5]	А3/Д3 [4]
(1,3)	(1,2)	(1,4,7)

Геометрическое складывание

2 ₂₁ связан с 24-ячейкой геометрическим сворачиванием диаграмм Коксетера-Дынкина E6/F4 . Это можно увидеть в проекциях плоскости Коксетера . 24 вершины 24-ячейки проецируются в те же два кольца, что и в 2 ₂₁ .

Е ₆	Ф ₄
2 ₂₁	24-ячеечный

Этот многогранник может разбить евклидово 6-мерное пространство на соты размером 2 ₂₂ с помощью следующей диаграммы Коксетера-Дынкина:.

Связанные сложные многогранники

Правильный комплексный многоугольник ₃ {3} ₃ {3} ₃ ,, имеет действительное представление в виде многогранника 2 ₂₁ , $\mathbb {C} ^{2}$ , в 4-мерном пространстве. Он называется многогранником Гесса в честь Эдмунда Гесса . Он имеет 27 вершин, 72 3-ребра и 27 3{3}3 граней. Его комплексная группа отражений равна ₃ [3] ₃ [3] ₃ , порядок 648.

Связанные многогранники

2 ₂₁ является четвертым в размерной серии полуправильных многогранников . Каждый прогрессивный однородный многогранник строится из вершинной фигуры предыдущего многогранника. Торольд Госсет определил эту серию в 1900 году как содержащую все грани правильного многогранника , содержащую все симплексы и ортоплексы .

k ₂₁ фигура в n измерениях
Космос	Конечный						Евклидов	Гиперболический
Е _н	3	4	5	6	7	8	9	10
Группа Коксетера	Э ₃ =А ₂ А ₁	Э ₄ =А ₄	Э ₅ =Д ₅	Е ₆	Е ₇	Е ₈	Э ₉ = = Э ₈⁺ ${\tilde {E}}_{8}$	Е ₁₀ = = Е ₈⁺⁺ ${\bar {T}}_{8}$
Диаграмма Коксетера
Симметрия	[3 ^−1,2,1 ]	[3 ^0,2,1 ]	[3 ^1,2,1 ]	[3 ^2,2,1 ]	[3 ^3,2,1 ]	[3 ^4,2,1 ]	[3 ^5,2,1 ]	[3 ^6,2,1 ]
Заказ	12	120	1,920	51,840	2,903,040	696,729,600	∞
График							-	-
Имя	−1 ₂₁	0 ₂₁	1 ₂₁	221	3 ₂₁	4 ₂₁	5 ₂₁	6 ₂₁

Многогранник 2 ₂₁ является четвертым в размерном ряду 2 _k2 .

2 _{k 1} фигур в n измерениях
Космос	Конечный						Евклидов	Гиперболический
н	3	4	5	6	7	8	9	10
Группа Коксетера	Э ₃ =А ₂ А ₁	Э ₄ =А ₄	Э ₅ =Д ₅	Е ₆	Е ₇	Е ₈	Э ₉ = = Э ₈⁺ ${\tilde {E}}_{8}$	Е ₁₀ = = Е ₈⁺⁺ ${\bar {T}}_{8}$
Диаграмма Коксетера
Симметрия	[3 ^−1,2,1 ]	[3 ^0,2,1 ]	[[3 ^1,2,1 ]]	[3 ^2,2,1 ]	[3 ^3,2,1 ]	[3 ^4,2,1 ]	[3 ^5,2,1 ]	[3 ^6,2,1 ]
Заказ	12	120	384	51,840	2,903,040	696,729,600	∞
График							-	-
Имя	2 _−1,1	2 ₀₁	2 ₁₁	221	2 ₃₁	2 ₄₁	2 ₅₁	2 ₆₁

Многогранник 2 ₂₁ является вторым в размерном ряду 2 _2k .

2 _2k фигур n измерений
Космос	Конечный			Евклидов	Гиперболический
н	4	5	6	7	8
Группа Коксетера	А ₂ А ₂	А ₅	Е ₆	${\tilde {E}}_{6}$ =Э ₆⁺	Е ₆⁺⁺
Диаграмма Коксетера
График				∞	∞
Имя	2 _2,-1	2 ₂₀	221	2 ₂₂	223

Выпрямленный 2_21 многогранник

Выпрямленный 2 ₂₁ многогранник
Тип	Однородный 6-многогранник
Символ Шлефли	т ₁ {3,3,3 ^2,1 }
символ Коксетера	т ₁ (2 ₂₁ )
Диаграмма Коксетера-Дынкина	или
5-гранный	Всего 126: 72 т ₁ {3 ⁴ } 27 т ₁ {3 ³ ,4} 27 т ₁ {3,3 ^2,1 }
4-х гранный	1350
Клетки	4320
Лица	5040
Края	2160
Вершины	216
Вершинная фигура	выпрямленная 5-ячеистая призма
Группа Коксетера	E ₆ , [3 ^2,2,1 ], заказ 51840
Характеристики	выпуклый

Выпрямленный 2 ₂₁ имеет 216 вершин и 126 граней: 72 выпрямленных 5-симплекса , 27 выпрямленных 5-ортоплексов и 27 5-демикубов . Его вершинная фигура — выпрямленная 5-ячейковая призма.

Альтернативные названия

Ректифицированный икосигепта-гептаконтиди-петон как ректифицированный 27-72-гранный полипетон (акроним роджак) (Джонатан Бауэрс) ^[6]

Строительство

Его конструкция основана на группе E ₆ , а информацию можно извлечь из кольцевой диаграммы Коксетера-Дынкина, представляющей этот многогранник:.

Сняв кольцо на короткой ветви, получаем выпрямленный 5-симплекс ,.

Удаление кольца на конце другой ветви длиной 2 оставляет выпрямленный 5-ортоплекс в его измененной форме: t ₁ (2 ₁₁ ) ,.

Удаление кольца на конце той же ветви длиной 2 оставляет 5-демикуб : (1 ₂₁ ) ,.

Вершинная фигура определяется путем удаления окольцованного кольца и окольцовывания соседнего кольца. Это дает выпрямленную 5-ячеистую призму, t ₁ {3,3,3}x{},.

Изображения

Вершины в этой проекции окрашены в порядке возрастания их кратности: красный, оранжевый, желтый.

Ортографические проекции плоскости Коксетера
Е6 [12]	Д5 [8]	Д4/А2 [6]

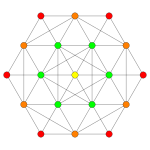А5 [6]	А4 [5]	А3/Д3 [4]

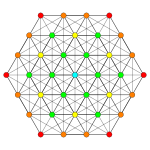Усеченный 2_21 многогранник

Усеченный 2 ₂₁ многогранник
Тип	Однородный 6-многогранник
Символ Шлефли	т{3,3,3 ^2,1 }
символ Коксетера	т(2 ₂₁ )
Диаграмма Коксетера-Дынкина	или
5-гранный	72+27+27
4-х гранный	432+216+432+270
Клетки	1080+2160+1080
Лица	720+4320
Края	216+2160
Вершины	432
Вершинная фигура	( ) вр{3,3,3}
Группа Коксетера	E ₆ , [3 ^2,2,1 ], заказ 51840
Характеристики	выпуклый

Усеченный 2 ₂₁ имеет 432 вершины, 5040 ребер, 4320 граней, 1350 ячеек и 126 4-граней. Его вершинная фигура — выпрямленная 5-ячеистая пирамида.

Изображения

Вершины в этой проекции окрашены в порядке возрастания их кратности: красный, оранжевый, желтый, зеленый, голубой, синий, фиолетовый.

Ортографические проекции плоскости Коксетера
Е6 [12]	Д5 [8]	Д4/А2 [6]

А5 [6]	А4 [5]	А3/Д3 [4]

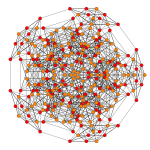Смотрите также

Список многогранников E6

Примечания

^ Госсет, 1900
^ Coxeter, HSM (1940). «Многогранник 2 ₂₁ , двадцать семь вершин которого соответствуют линиям на общей кубической поверхности». Amer. J. Math . 62 (1): 457– 486. doi :10.2307/2371466. JSTOR 2371466.
^ Элте, 1912
^ Клитцинг, (x3o3o3o3o *c3o - jak)
^ Коксетер, Регулярные многогранники, 11.8 Фигуры Госсета в шести, семи и восьми измерениях, стр. 202-203
^ Клитцинг, (o3x3o3o3o *c3o - роджак)

Ссылки

Т. Госсет : О правильных и полуправильных фигурах в пространстве n измерений , Вестник математики, Макмиллан, 1900
Элте, Э.Л. (1912), Полуправильные многогранники гиперпространств , Гронинген: Университет Гронингена
Калейдоскопы: избранные труды Х. С. М. Коксетера , под редакцией Ф. Артура Шерка, Питера МакМаллена, Энтони К. Томпсона, Азии Айвик Вайс, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [1]
- (Документ 17) Коксетер , Эволюция диаграмм Кокстера-Динкина , [Nieuw Archief voor Wiskunde 9 (1991) 233-248] См. рисунок 1: (стр. 232) (Граф узловых ребер многогранника)
Клитцинг, Ричард. «6D однородные многогранники (полипеты)».x3o3o3o3o *c3o - як, o3x3o3o3o *c3o - рожак

в т е Фундаментальные выпуклые правильные и однородные многогранники в размерностях 2–10
Семья	А _н	Б _н	Я ₂ (п) / Д _н	Е ₆ / Е ₇ / Е ₈ / Ф ₄ / Соль ₂	Н _н
Правильный многоугольник	Треугольник	Квадрат	п-гон	Шестиугольник	Пентагон
Однородный многогранник	Тетраэдр	Октаэдр • Куб	Демикуб		Додекаэдр • Икосаэдр
Равномерный полихорон	Пентахорон	16-ячеечный • Тессеракт	Демитессеракт	24-ячеечный	120-ячеечный • 600-ячеечный
Однородный 5-многогранник	5-симплекс	5-ортоплекс • 5-куб	5-демикуб
Однородный 6-многогранник	6-симплекс	6-ортоплекс • 6-куб	6-демикуб	1 ₂₂ • 221
Однородный 7-многогранник	7-симплекс	7-ортоплекс • 7-куб	7-демикуб	1 ₃₂ • 2 ₃₁ • 3 ₂₁
Однородный 8-многогранник	8-симплекс	8-ортоплекс • 8-куб	8-демикуб	1 ₄₂ • 2 ₄₁ • 4 ₂₁
Однородный 9-многогранник	9-симплекс	9-ортоплекс • 9-куб	9-демикуб
Однородный 10-многогранник	10-симплекс	10-ортоплекс • 10-куб	10-демикуб
Однородный n - многогранник	н - симплекс	n - ортоплекс • n - куб	н - демикуб	1 _к2 • 2 _к1 • к ₂₁	n - пятиугольный многогранник
Темы: Семейства многогранников • Правильный многогранник • Список правильных многогранников и соединений

[1] Госсет, 1900

[2] Coxeter, HSM (1940). «Многогранник 2 ₂₁ , двадцать семь вершин которого соответствуют линиям на общей кубической поверхности». Amer. J. Math . 62 (1): 457– 486. doi :10.2307/2371466. JSTOR 2371466.

[3] Элте, 1912

[4] Клитцинг, (x3o3o3o3o *c3o - jak)

[5] Коксетер, Регулярные многогранники, 11.8 Фигуры Госсета в шести, семи и восьми измерениях, стр. 202-203

[6] Клитцинг, (o3x3o3o3o *c3o - роджак)