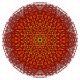
Пентик 6-кубовый

6-демикуб
(половина 6-куба)
=
Пентик 6-кубовый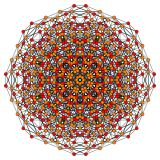
=
Пентикантик 6-кубовый
=

Пентирунчик 6-кубовый
=
Пентирунцикантик 6-кубовый
=
Пентистерик 6-кубовый
=

Пентистерикантический 6-кубовый
=
Пентистерирунический 6-кубовый
=
Пентистерирунцикантик 6-кубовый
=
Ортогональные проекции в плоскости Коксетера D 6

В шестимерной геометрии пентичный 6-куб является выпуклым однородным 6-многогранником .

Существует 8 пентических форм 6-куба.

Пентик 6-кубовый

Пентик 6-кубовый
Типоднородный 6-многогранник
Символ Шлефлит 0,4 {3,3 4,1 }
ч 5 {4,3 4 }
Диаграмма Коксетера-Дынкина=
5-гранный
4-х гранный
Клетки
Лица
Края1440
Вершины192
Вершинная фигура
Группы КоксетераД 6 , [3 3,1,1 ]
Характеристикивыпуклый

Пентик 6-куб ,, имеет половину вершин пятиугольного 6-куба ,.

Альтернативные названия

  • Стерилизованный 6-демикуб/демигексеракт
  • Малый клеточный гемигексеракт (сокращение: sochax) (Джонатан Бауэрс) [1]

Декартовы координаты

Декартовы координаты вершин с центром в начале координат представляют собой перестановки координат:

(±1,±1,±1,±1,±1,±3)

с нечетным числом знаков плюс.

Изображения

ортографические проекции
самолет КоксетераБ 6
График
Диэдральная симметрия[12/2]
самолет КоксетераД 6Д 5
График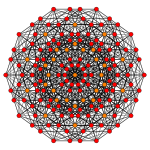
Диэдральная симметрия[10][8]
самолет КоксетераД 4Д 3
График
Диэдральная симметрия[6][4]
самолет КоксетераА 5А 3
График
Диэдральная симметрия[6][4]

Пентикантик 6-кубовый

Пентикантик 6-кубовый
Типоднородный 6-многогранник
Символ Шлефлит 0,1,4 {3,3 4,1 }
ч 2,5 {4,3 4 }
Диаграмма Коксетера-Дынкина=
5-гранный
4-х гранный
Клетки
Лица
Края9600
Вершины1920
Вершинная фигура
Группы КоксетераД 6 , [3 3,1,1 ]
Характеристикивыпуклый

Пентикантический 6-куб ,, имеет половину вершин пятиугольного 6-куба ,.

Альтернативные названия

  • Стери-усеченный 6-демикуб/демигексеракт
  • укороченный гемигексеракт (сокращение: cathix) (Джонатан Бауэрс) [2]

Декартовы координаты

Декартовы координаты вершин с центром в начале координат представляют собой перестановки координат:

(±1,±1,±3,±3,±3,±5)

с нечетным числом знаков плюс.

Изображения

ортографические проекции
самолет КоксетераБ 6
График
Диэдральная симметрия[12/2]
самолет КоксетераД 6Д 5
График
Диэдральная симметрия[10][8]
самолет КоксетераД 4Д 3
График
Диэдральная симметрия[6][4]
самолет КоксетераА 5А 3
График
Диэдральная симметрия[6][4]

Пентирунчик 6-кубовый

Пентирунчик 6-кубовый
Типоднородный 6-многогранник
Символ Шлефлит 0,2,4 {3,3 4,1 }
ч 3,5 {4,3 4 }
Диаграмма Коксетера-Дынкина=
5-гранный
4-х гранный
Клетки
Лица
Края10560
Вершины1920
Вершинная фигура
Группы КоксетераД 6 , [3 3,1,1 ]
Характеристикивыпуклый

Пентирунчический 6-куб ,, имеет половину вершин пятилучевого 6-куба (пятилучевой 6-ортоплекс),.

Альтернативные названия

  • Стерилизованный 6-демикуб/демигексеракт
  • целлиромбированный гемигексеракт (сокращение: crohax) (Джонатан Бауэрс) [3]

Декартовы координаты

Декартовы координаты вершин с центром в начале координат представляют собой перестановки координат:

(±1,±1,±1,±3,±3,±5)

с нечетным числом знаков плюс.

Изображения

ортографические проекции
самолет КоксетераБ 6
График
Диэдральная симметрия[12/2]
самолет КоксетераД 6Д 5
График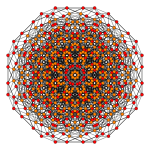
Диэдральная симметрия[10][8]
самолет КоксетераД 4Д 3
График
Диэдральная симметрия[6][4]
самолет КоксетераА 5А 3
График
Диэдральная симметрия[6][4]

Пентирунцикантик 6-кубовый

Пентирунцикантик 6-кубовый
Типоднородный 6-многогранник
Символ Шлефлит 0,1,2,4 {3,3 2,1 }
ч 2,3,5 {4,3 4 }
Диаграмма Коксетера-Дынкина=
5-гранный
4-х гранный
Клетки
Лица
Края20160
Вершины5760
Вершинная фигура
Группы КоксетераД 6 , [3 3,1,1 ]
Характеристикивыпуклый

Пентирунцикантический 6-куб ,, имеет половину вершин пентирунцикантеллированного 6-куба или (пентирунцикантеллированного 6-ортоплекса),

Альтернативные названия

  • Стерилизукороченный демигексацикл, стерически укороченный 7-демикуб
  • Большой клеточный гемигексеракт (сокращение: cagrohax) (Джонатан Бауэрс) [4]

Декартовы координаты

Декартовы координаты вершин с центром в начале координат представляют собой перестановки координат:

(±1,±1,±3,±3,±5,±7)

с нечетным числом знаков плюс.

Изображения

ортографические проекции
самолет КоксетераБ 6
График
Диэдральная симметрия[12/2]
самолет КоксетераД 6Д 5
График
Диэдральная симметрия[10][8]
самолет КоксетераД 4Д 3
График
Диэдральная симметрия[6][4]
самолет КоксетераА 5А 3
График
Диэдральная симметрия[6][4]

Пентистерик 6-кубовый

Пентистерик 6-кубовый
Типоднородный 6-многогранник
Символ Шлефлит 0,3,4 {3,3 4,1 }
ч 4,5 {4,3 4 }
Диаграмма Коксетера-Дынкина=
5-гранный
4-х гранный
Клетки
Лица
Края5280
Вершины960
Вершинная фигура
Группы КоксетераД 6 , [3 3,1,1 ]
Характеристикивыпуклый

Пентистерический 6-куб ,, имеет половину вершин пентистерированного 6-куба (пентитеркированного 6-ортоплекса),

Альтернативные названия

  • Стерилизованный 6-демикуб/демигексеракт
  • Малый клеточно-приматный гемигексеракт (сокращение: cophix) (Джонатан Бауэрс) [5]

Декартовы координаты

Декартовы координаты вершин с центром в начале координат представляют собой перестановки координат:

(±1,±1,±1,±1,±3,±5)

с нечетным числом знаков плюс.

Изображения

ортографические проекции
самолет КоксетераБ 6
График
Диэдральная симметрия[12/2]
самолет КоксетераД 6Д 5
График
Диэдральная симметрия[10][8]
самолет КоксетераД 4Д 3
График
Диэдральная симметрия[6][4]
самолет КоксетераА 5А 3
График
Диэдральная симметрия[6][4]

Пентистерикантический 6-кубовый

Пентистерикантический 6-кубовый
Типоднородный 6-многогранник
Символ Шлефлит 0,1,3,4 {3,3 4,1 }
ч 2,4,5 {4,3 4 }
Диаграмма Коксетера-Дынкина=
5-гранный
4-х гранный
Клетки
Лица
Края23040
Вершины5760
Вершинная фигура
Группы КоксетераД 6 , [3 3,1,1 ]
Характеристикивыпуклый

Пентистерикантический 6-кубовый ,, имеет половину вершин пентистерико-усеченного 6-куба (пентирунцитрусцированный 6-ортоплекс),.

Альтернативные названия

  • Стерилизованный усеченный демигексеракт/7-демикуб
  • укороченный гемигексеракт (сокращение: каптикс) (Джонатан Бауэрс) [6]

Декартовы координаты

Декартовы координаты вершин с центром в начале координат представляют собой перестановки координат:

(±1,±1,±3,±3,±5,±7)

с нечетным числом знаков плюс.

Изображения

ортографические проекции
самолет КоксетераБ 6
График
Диэдральная симметрия[12/2]
самолет КоксетераД 6Д 5
График
Диэдральная симметрия[10][8]
самолет КоксетераД 4Д 3
График
Диэдральная симметрия[6][4]
самолет КоксетераА 5А 3
График
Диэдральная симметрия[6][4]

Пентистерирунический 6-кубовый

Пентистерирунический 6-кубовый
Типоднородный 6-многогранник
Символ Шлефлит 0,2,3,4 {3,3 4,1 }
ч 3,4,5 {4,3 4 }
Диаграмма Коксетера-Дынкина=
5-гранный
4-х гранный
Клетки
Лица
Края15360
Вершины3840
Вершинная фигура
Группы КоксетераД 6 , [3 3,1,1 ]
Характеристикивыпуклый

Пентистерирунический 6-кубовый ,, имеет половину вершин пентистерирцинированного 6-куба (пентистерирцинированный 6-ортоплекс),.

Альтернативные названия

  • Стерилизованный 6-демикуб/демигексеракт
  • Целлипризматоромбатированный гемигексеракт (сокращение: капрохакс) (Джонатан Бауэрс) [7]

Декартовы координаты

Декартовы координаты вершин с центром в начале координат представляют собой перестановки координат:

(±1,±1,±1,±3,±5,±7)

с нечетным числом знаков плюс.

Изображения

ортографические проекции
самолет КоксетераБ 6
График
Диэдральная симметрия[12/2]
самолет КоксетераД 6Д 5
График
Диэдральная симметрия[10][8]
самолет КоксетераД 4Д 3
График
Диэдральная симметрия[6][4]
самолет КоксетераА 5А 3
График
Диэдральная симметрия[6][4]

Пентистерирунцикантик 6-кубовый

Пентистерирунцикантик 6-кубовый
Типоднородный 6-многогранник
Символ Шлефлит 0,1,2,3,4 {3,3 2,1 }
ч 2,3,4,5 {4,3 4 }
Диаграмма Коксетера-Дынкина=
5-гранный
4-х гранный
Клетки
Лица
Края34560
Вершины11520
Вершинная фигура
Группы КоксетераД 6 , [3 3,1,1 ]
Характеристикивыпуклый

Пентистерирунцикантик 6-кубовый ,, имеет половину вершин пентистерирунцикантитулированного 6-куба (пентистерирунцикантитулированный 6-ортоплекс),.

Альтернативные названия

  • Стерирунцикантитрированный 6-демикуб/демигексеракт
  • Большой ячеистый гемигексеракт (сокращение: gochax) (Джонатан Бауэрс) [8]

Декартовы координаты

Декартовы координаты вершин с центром в начале координат представляют собой перестановки координат:

(±1,±1,±3,±3,±5,±7)

с нечетным числом знаков плюс.

Изображения

ортографические проекции
самолет КоксетераБ 6
График
Диэдральная симметрия[12/2]
самолет КоксетераД 6Д 5
График
Диэдральная симметрия[10][8]
самолет КоксетераД 4Д 3
График
Диэдральная симметрия[6][4]
самолет КоксетераА 5А 3
График
Диэдральная симметрия[6][4]

Существует 47 однородных многогранников с симметрией D6 , 31 из них имеют симметрию B6 , а 16 являются уникальными:

Многогранники D6

ч{4,3 4 }
ч 2 {4,3 4 }
ч 3 {4,3 4 }
ч 4 {4,3 4 }
ч 5 {4,3 4 }
ч 2,3 {4,3 4 }
ч 2,4 {4,3 4 }
ч 2,5 {4,3 4 }

ч 3,4 {4,3 4 }
ч 3,5 {4,3 4 }
ч 4,5 {4,3 4 }
ч 2,3,4 {4,3 4 }
ч 2,3,5 {4,3 4 }
ч 2,4,5 {4,3 4 }
ч 3,4,5 {4,3 4 }
ч 2,3,4,5 {4,3 4 }

Примечания

  1. ^ Клитцинг, (x3o3o *b3o3x3o3o - sochax)
  2. ^ Клитцинг, (x3x3o *b3o3x3o3o - катикс)
  3. ^ Клитцинг, (x3o3o *b3x3x3o3o - crohax)
  4. ^ Клитцинг, (x3x3o *b3x3x3o3o - cagrohax)
  5. ^ Клитцинг, (x3o3o *b3o3x3x3x - копикс)
  6. ^ Клитцинг, (x3x3o *b3o3x3x3x - каптикс)
  7. ^ Клитцинг, (x3o3o *b3x3x3x3x - капрохакс)
  8. ^ Клитцинг, (x3x3o *b3x3x3x3o - gochax)

Ссылки

  • HSM Коксетер :
    • HSM Coxeter, Правильные многогранники , 3-е издание, Довер, Нью-Йорк, 1973
    • Калейдоскопы: избранные труды Х. С. М. Коксетера , под редакцией Ф. Артура Шерка, Питера МакМаллена, Энтони К. Томпсона, Азии Айвик Вайс, Wiley-Interscience Publication, 1995, ISBN  978-0-471-01003-6 [1]
      • (Документ 22) HSM Coxeter, Правильные и полуправильные многогранники I , [Math. Zeit. 46 (1940) 380–407, MR 2,10]
      • (Документ 23) HSM Coxeter, Правильные и полуправильные многогранники II , [Math. Zeit. 188 (1985) 559-591]
      • (Документ 24) HSM Coxeter, Правильные и полуправильные многогранники III , [Math. Zeit. 200 (1988) 3-45]
  • Норман Джонсон Однородные многогранники , Рукопись (1991)
    • Н. В. Джонсон: Теория однородных многогранников и сот , доктор философии.
  • Клитцинг, Ричард. «6D однородные многогранники (полипеты)».x3o3o *b3o3x3o3o - sochax, x3x3o *b3o3x3o3o - catix, x3o3o *b3x3x3o3o - crohax, x3x3o *b3x3x3o3o - cagrohax, x3o3o *b3o3x3x3x - cophix, x3x3o *b3o3x3x3x - capthix, x3o3o *b3x3x3x3x - caprohax, x3x3o *b3x3x3x3o - gochax
Фундаментальные выпуклые правильные и однородные многогранники в размерностях 2–10
СемьяА нБ нЯ 2 (п) / Д нЕ 6 / Е 7 / Е 8 / Ф 4 / Соль 2Н н
Правильный многоугольникТреугольникКвадратп-гонШестиугольникПентагон
Однородный многогранникТетраэдрОктаэдр • КубДемикубДодекаэдр • Икосаэдр
Равномерный полихоронПентахорон16-ячеечный • ТессерактДемитессеракт24-ячеечный120-ячеечный • 600-ячеечный
Однородный 5-многогранник5-симплекс5-ортоплекс • 5-куб5-демикуб
Однородный 6-многогранник6-симплекс6-ортоплекс • 6-куб6-демикуб1 22 • 2 21
Однородный 7-многогранник7-симплекс7-ортоплекс • 7-куб7-демикуб1 32 • 2 31 • 3 21
Однородный 8-многогранник8-симплекс8-ортоплекс • 8-куб8-демикуб1 42 • 2 41 • 4 21
Однородный 9-многогранник9-симплекс9-ортоплекс • 9-куб9-демикуб
Однородный 10-многогранник10-симплекс10-ортоплекс • 10-куб10-демикуб
Однородный n - многогранникн - симплексn - ортоплекс • n - кубн - демикуб1 к2 • 2 к1 • к 21n - пятиугольный многогранник
Темы: Семейства многогранников • Правильный многогранник • Список правильных многогранников и соединений
Взято с "https://en.wikipedia.org/w/index.php?title=Pentic_6-cubes&oldid=1243640469#Pentisteriruncicantic_6-cube"