Пятиугольный купол
| Пятиугольный купол | |
|---|---|
 | |
| Тип | Джонсон Дж 4 – Дж 5 – Дж 6 |
| Лица | 5 треугольников 5 квадратов 1 пятиугольник 1 десятиугольник |
| Края | 25 |
| Группа симметрии | |
| Характеристики | выпуклый , элементарный |
| Сеть | |
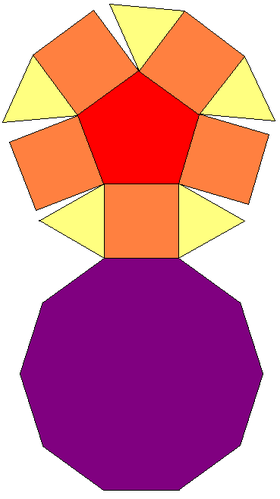 | |
Характеристики
Грани пятиугольного купола представляют собой пять равносторонних треугольников , пять квадратов , один правильный пятиугольник и один правильный десятиугольник . [1] Он обладает свойством выпуклости и правильными многоугольными гранями, благодаря чему он классифицируется как пятое тело Джонсона . [2] Этот купол образует два или более правильных многогранника путем разрезания его плоскостью, пример элементарного многогранника . [3]
Следующие формулы для радиуса описанной окружности , высоты , площади поверхности и объема могут быть применены, если все грани являются правильными с длиной ребра : [4]
Он имеет ось симметрии, проходящую через центр как вершины, так и основания, которая симметрична при вращении вокруг нее на одну, две, три и четыре пятых угла полного оборота. Он также зеркально симметричен относительно любой перпендикулярной плоскости, проходящей через биссектрису шестиугольного основания. Поэтому он имеет пирамидальную симметрию , циклическую группу порядка десять. [3]
Связанный многогранник
Пятиугольный купол может быть использован для построения многогранника . Конструкция, которая включает присоединение его основания к другому многограннику, известна как аугментация ; присоединение его к призмам или антипризмам известно как удлинение или гироудлинение . [5] [6] Некоторые тела Джонсона с такими конструкциями: удлиненный пятиугольный купол , гироудлиненный пятиугольный купол , пятиугольный ортобикупол , пятиугольный гиробикупол , пятиугольная ортокуполо-ротонда, пятиугольная гирокуполо-ротонда , удлиненный пятиугольный ортобикупол , удлиненный пятиугольный гиробикупол , удлиненный пятиугольный ортокуполо- ротонда , гироудлиненный пятиугольный бикупол , гироудлиненный пятиугольный куполо-ротонда , наращенный усеченный додекаэдр , парабиоудлиненный усеченный додекаэдр , метабиоудлиненный усеченный додекаэдр , триаугментированный усеченный додекаэдр , гиратный ромбоикосододекаэдр , парабивиратный ромбоикосододекаэдр , метабивиратный ромбоикосододекаэдр и тривиратный ромбоикосододекаэдр . Соответственно, построение из многогранников путем удаления одного или нескольких пятиугольных куполов известно как уменьшение : уменьшенный ромбоикосододекаэдр , парагиратный уменьшенный ромбоикосододекаэдр , метагиратный уменьшенный ромбоикосододекаэдр , бигиратный уменьшенный ромбоикосододекаэдр , парабидиминизироанный ромбоикосододекаэдр , метабидиминизироанный ромбоикосододекаэдр , гиратный бидиминизироанный ромбоикосододекаэдр и тридиминизироанный ромбоикосододекаэдр . [1]
Ссылки
- ^ ab Берман, Мартин (1971). «Выпуклые многогранники с правильными гранями». Журнал Института Франклина . 291 (5): 329– 352. doi :10.1016/0016-0032(71)90071-8. MR 0290245.
- ^ Уэхара, Рюхэй (2020). Введение в вычислительное оригами: мир новой вычислительной геометрии. Springer. стр. 62. doi :10.1007/978-981-15-4470-5. ISBN 978-981-15-4470-5. S2CID 220150682.
- ^ ab Джонсон, Норман В. (1966). «Выпуклые многогранники с правильными гранями». Канадский журнал математики . 18 : 169– 200. doi : 10.4153/cjm-1966-021-8 . MR 0185507. S2CID 122006114. Zbl 0132.14603.
- ^ Braileanu1, Patricia I.; Cananaul, Sorin; Pasci, Nicoleta E. (2022). «Влияние геометрического узора заполнения на механическое поведение пятиугольного купола при статических внешних нагрузках». Журнал исследований и инноваций для устойчивого общества . 4 (2). Издательство Thoth: 5–15 . doi : 10.33727/JRISS.2022.2.1:5-15 (неактивно 16 декабря 2024 г.). ISSN 2668-0416.
{{cite journal}}: CS1 maint: DOI inactive as of December 2024 (link) CS1 maint: numeric names: authors list (link) - ^ Демей, Лоренц; Смессарт, Ганс (2017). «Логическое и геометрическое расстояние в многогранных аристотелевских диаграммах в представлении знаний». Симметрия . 9 (10): 204. Bibcode : 2017Symm....9..204D. doi : 10.3390/sym9100204 .
- ^ Слободан, Мишич; Обрадович, Мария; Джуканович, Гордана (2015). «Композитные вогнутые купола как геометрические и архитектурные формы» (PDF) . Журнал геометрии и графики . 19 (1): 79–91 .
Внешние ссылки
- Вайсштейн, Эрик В. , «Пентагональный купол» («тело Джонсона») на MathWorld .


































