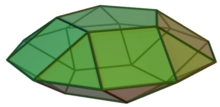
Пятиугольный гиробикупол

Пятиугольный гиробикупол
Тип	Бикупола , Джонсон J 30 – J 31 – J 32
Лица	10 треугольников 10 квадратов 2 пятиугольника
Края	40
Вершины	20
Конфигурация вершины	${\displaystyle 10\times (3\times 4\times 3\times 4)}$ ${\displaystyle 10\times (3\times 4\times 5\times 4)}$
Группа симметрии	${\displaystyle D_{5\mathrm {d} }}$
Характеристики	выпуклый , составной
Сеть

Пятиугольный гиробикупол — это многогранник, который построен путем присоединения двух пятиугольных куполов основанием к основанию, каждый из его куполов закручен на 36°. Это пример тела Джонсона и составного многогранника .

Пятиугольный гиробикупол — это составной многогранник : он построен путем присоединения двух пятиугольных куполов основанием к основанию. Эта конструкция похожа на пятиугольный ортобикупол ; разница в том, что один из куполов в пятиугольном гиробикуполе закручен на 36°, как предполагает префикс гиро- . Полученный многогранник имеет те же грани, что и пятиугольный ортобикупол: эти купола покрывают свои десятиугольные основания, заменяя их восемью равносторонними треугольниками , восемью квадратами и двумя правильными пятиугольниками . ^[1] Выпуклый многогранник , в котором все его грани являются правильными многоугольниками, называется телом Джонсона . Пятиугольный гиробикупол имеет такие, что перечисляет его как тридцать первое тело Джонсона . ^[2]${\displaystyle J_{31}}$

Поскольку конструкция пятиугольного гиробикупола аналогична конструкции пятиугольного ортобикупола, площадь поверхности пятиугольного гиробикупола равна сумме площадей многоугольных граней, а его объем в два раза превышает объем пятиугольного купола, для которого его разрезают на следующие части: ^[1]${\displaystyle А}$${\displaystyle V}$$${\displaystyle {\begin{aligned}A&={\frac {20+{\sqrt {100+10{\sqrt {5}}+10{\sqrt {75+30{\sqrt {5}}}}}}}{2}}a^{2}\approx 17.771a^{2},\\V&={\frac {5+4{\sqrt {5}}}{3}}a^{3}\approx 4.648a^{3}.\end{aligned}}}$$

• Вайсштейн, Эрик В. , «Пентагональная гиробикупола» («тело Джонсона») на MathWorld .