Ирригированный ромбоикосододекаэдр

Ирригированный ромбоикосододекаэдр
Ирригированный ромбоикосододекаэдр
Тип	Канонический многогранник ; Джонсон ; J 71 – J 72 – J 73
Лица	20 треугольников ; 30 квадратов ; 12 пятиугольников
Края	120
Вершины	60
Конфигурация вершины	10 × ( 3 × 4 2 × 5 ) + 4 × 5 + 3 × 10 × ( 3 × 4 × 5 × 4 ) {\displaystyle {\begin{aligned}&10\times (3\times 4^{2}\times 5)+\\&4\times 5+3\times 10\times (3\times 4\times 5\times 4)\end{aligned}}}
Группа симметрии	C 5 v {\displaystyle C_{5v}}
Характеристики	выпуклый , ; свойство Руперта
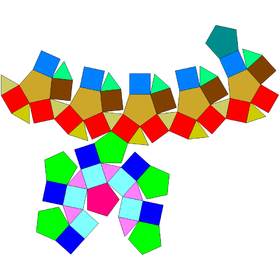
Сеть

72-й Джонсон солидный

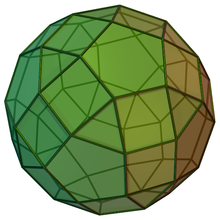
В геометрии ромбоикосододекаэдр является одним из тел Джонсона ( $J$ $72$ ) . Он также является каноническим многогранником .

Тело Джонсона — один из 92 строго выпуклых многогранников , которые состоят из правильных многоугольных граней, но не являются однородными многогранниками (то есть они не являются Платоновыми телами , Архимедовыми телами , призмами или антипризмами ). Они были названы Норманом Джонсоном , который впервые перечислил эти многогранники в 1966 году. ^[1]

Строительство

Спиральный ромбоикосододекаэдр может быть построен аналогично ромбоикосододекаэдру : он построен из парабидоуменьшенного ромбоикосододекаэдра путем присоединения двух правильных пятиугольных куполов к его десятиугольным граням. В результате эти пятиугольные купола покрывают его додекагональные грани, так что полученный многогранник имеет 20 равносторонних треугольников , 30 квадратов и 10 правильных пятиугольников в качестве своих граней. Разница между этими двумя многогранниками заключается в том, что один из двух пятиугольных куполов из спирального ромбоикосододекаэдра повернут на 36°. [ ^2] Выпуклый многогранник, в котором все грани являются правильными многоугольниками, называется телом Джонсона , и спиральный ромбоикосододекаэдр входит в их число, поименованный как 72-е тело Джонсона . ^[3] $J_{72}$

Разница между ромбоикосододекаэдром (слева) и изогнутым ромбоикосододекаэдром (справа) по их строению

Характеристики

Поскольку два вышеупомянутых многогранника имеют схожую конструкцию, они имеют одинаковую площадь поверхности и объем. Иратный ромбоикосододекаэдр с длиной ребра имеет площадь поверхности, складывая все площади его граней: ^[2] Его объем можно вычислить, разрезав его на два правильных пятиугольных купола и один парабииратный ромбоикосододекаэдр, и сложив их объемы: ^[2] $\left(30+5{\sqrt {3}}+3{\sqrt {25+10{\sqrt {5}}}}\right)a^{2}\approx 59.306a^{2}.$ ${\frac {60+29{\sqrt {5}}}{3}}a^{3}\approx 41.615a^{3}.$

Гиратный ромбоикосододекаэдр — одно из пяти тел Джонсона, не обладающих свойством Руперта , то есть многогранником того же или большего размера и той же формы, что и он, который не может пройти через отверстие в нем. Другие тела Джонсона, не обладающие таким свойством, — это парабигиратный ромбоикосододекаэдр , метабигиратный ромбоикосододекаэдр , тригиратный ромбоикосододекаэдр и парагиратный уменьшенный ромбоикосододекаэдр . ^[4]

Смотрите также

Альтернативные тела Джонсона, построенные путем вращения различных куполов ромбоикосододекаэдра, следующие:

Парабигоритовый ромбоикосододекаэдр , в котором два противолежащих купола повернуты; $J_{73}$
Метабигиратный ромбоикосододекаэдр , в котором повернуты два непротивоположных купола; $J_{74}$
И тривиальный ромбоикосододекаэдр , в котором повернуты три купола. $J_{75}$

Ссылки

^ Джонсон, Норман В. (1966), «Выпуклые многогранники с правильными гранями», Канадский журнал математики , 18 : 169–200 , doi :10.4153/cjm-1966-021-8, MR 0185507, Zbl 0132.14603.
^ abc Берман, Мартин (1971), «Выпуклые многогранники с правильными гранями», Журнал Института Франклина , 291 (5): 329–352 , doi :10.1016/0016-0032(71)90071-8, MR 0290245 .
^ Фрэнсис, Даррил (август 2013 г.), «Твердые тела Джонсона и их аббревиатуры», Word Ways , 46 (3): 177.
^ Фредрикссон, Альбин (2024), «Оптимизация для свойства Руперта», The American Mathematical Monthly , 131 (3): 255–261 , arXiv : 2210.00601 , doi : 10.1080/00029890.2023.2285200.

Внешние ссылки

Вайсштейн, Эрик В. , «Витой ромбоикосододекаэдр» («тело Джонсона») на сайте MathWorld .

[1] Джонсон, Норман В. (1966), «Выпуклые многогранники с правильными гранями», Канадский журнал математики , 18 : 169–200 , doi :10.4153/cjm-1966-021-8, MR 0185507, Zbl 0132.14603.

[berman-2] Берман, Мартин (1971), «Выпуклые многогранники с правильными гранями», Журнал Института Франклина , 291 (5): 329–352 , doi :10.1016/0016-0032(71)90071-8, MR 0290245 .

[francis-3] Фрэнсис, Даррил (август 2013 г.), «Твердые тела Джонсона и их аббревиатуры», Word Ways , 46 (3): 177.

[fred-4] Фредрикссон, Альбин (2024), «Оптимизация для свойства Руперта», The American Mathematical Monthly , 131 (3): 255–261 , arXiv : 2210.00601 , doi : 10.1080/00029890.2023.2285200.

Ирригированный ромбоикосододекаэдр

Тип	Канонический многогранник Джонсон $J 71 - J 72 - J 73$
Лица	20 треугольников 30 квадратов 12 пятиугольников
Края	120
Вершины	60
Конфигурация вершины	${\begin{aligned}&10\times (3\times 4^{2}\times 5)+\\&4\times 5+3\times 10\times (3\times 4\times 5\times 4)\end{aligned}}$
Группа симметрии	$C_{5v}$
Характеристики	выпуклый , свойство Руперта
Сеть