Удлиненный пятиугольный ортобикупол

Удлиненный пятиугольный ортобикупол
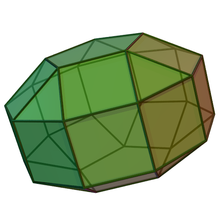Тип	Джонсон Дж 37 – Дж 38 – Дж 39
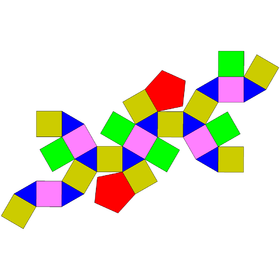
Лица	10 треугольников 2x5+10 квадратов 2 пятиугольника
Края	60
Вершины	30
Конфигурация вершины	20(3.4 3 ) 10(3.4.5.4)
Группа симметрии	Д 5ч
Двойной многогранник	-
Характеристики	выпуклый
Сеть

В геометрии удлиненный пятиугольный ортобикупол или скошенная пятиугольная призма является одним из тел Джонсона ( J ₃₈ ). ^[1] Как следует из названия, его можно построить, удлиняя пятиугольный ортобикупол ( J ₃₀ ) путем вставки десятиугольной призмы между его двумя конгруэнтными половинами. Поворот одного из куполов на 36 градусов перед вставкой призмы дает удлиненный пятиугольный гиробикупол ( J ₃₉ ).

Тело Джонсона — один из 92 строго выпуклых многогранников , которые состоят из правильных многоугольных граней, но не являются однородными многогранниками (то есть они не являются Платоновыми телами , Архимедовыми телами , призмами или антипризмами ). Они были названы Норманом Джонсоном , который впервые перечислил эти многогранники в 1966 году. ^[2]

Следующие формулы для объема и площади поверхности можно использовать, если все грани правильные , с длиной ребра a : ^[3]

${\displaystyle V={\frac {1}{6}}\left(10+8{\sqrt {5}}+15{\sqrt {5+2{\sqrt {5}}}}\right)a^{3}\approx 12.3423...a^{3}}$

${\displaystyle A=\left(20+{\sqrt {{\frac {5}{2}}\left(10+{\sqrt {5}}+{\sqrt {75+30{\sqrt {5}}}}\right)}}\right)a^{2}\approx 27.7711...a^{2}}$

• Вайсштейн, Эрик В. , «Удлиненный пятиугольный ортобикупол» («тело Джонсона») на MathWorld .

Эта статья о многогранниках — заглушка . Вы можете помочь Википедии, расширив ее.

• в
• т
• е