Список сферических групп симметрии

Выбранные группы точек в трех измерениях
Полиэдральная группа , [n,3], (*n32)
Инволюционная симметрия C _s , (*) [ ] =	Циклическая симметрия C _nv , (*nn) [n] =	Диэдральная симметрия D _nh , (*n22) [n,2] =
Тетраэдрическая симметрия T _d , (*332) [3,3] =	Октаэдрическая симметрия O _h , (*432) [4,3] =	Икосаэдрическая симметрия I _h , (*532) [5,3] =

Конечные сферические группы симметрии также называются точечными группами в трех измерениях . Существует пять фундаментальных классов симметрии, которые имеют треугольные фундаментальные области: диэдральная , циклическая , тетраэдральная , октаэдральная и икосаэдрическая симметрия.

В этой статье перечислены группы по нотации Шёнфлиса , нотации Коксетера , ^[1] орбифолдной нотации , ^[2] и порядку. Джон Конвей использует вариацию нотации Шёнфлиса, основанную на кватернионной алгебраической структуре групп, помеченную одной или двумя заглавными буквами и целыми индексами. Порядок группы определяется как нижний индекс, если только порядок не удваивается для символов с префиксом плюс или минус, "±", что подразумевает центральную инверсию . ^[3]

Также дана нотация Германа–Могена (международная нотация). Кристаллографические группы, всего 32, представляют собой подмножество с порядками элементов 2, 3, 4 и 6. ^[4]

Инволюционная симметрия

Существует четыре инволюционные группы: отсутствие симметрии (C ₁ ), зеркальная симметрия (C _s ), 2-кратная вращательная симметрия (C ₂ ) и центральная точечная симметрия (C _i ).

Международный	Гео	Орбифолд	Шёнфлис	Конвей	Коксетер	Заказ	Абстрактный
1	1	11	С ₁	С ₁	][ [ ] ⁺	1	Я ₁
2	2	22	Д ₁ = С ₂	Д2 = _С2	[2] ⁺	2	Z2
1	22	×	С _i = S ₂	СС ₂	[2 ⁺ ,2 ⁺ ]	2	Z2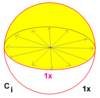
2 = м	1	*	С _с = С _1в = С _1ч	±С ₁ = КД ₂	[ ]	2	Z2

Циклическая симметрия

Существует четыре бесконечных циклических семейства симметрии , где n = 2 или выше. ( n может быть равно 1 как особый случай, так как симметрия отсутствует )

Международный	Гео	Орбифолд	Шёнфлис	Конвей	Коксетер		Заказ	Абстрактный	Фонд. домен
4	42	2×	С ₄	СС ₄	[2 ⁺ ,4 ⁺ ]		4	Я ₄
2/м	2 2	2*	С _2ч = Д _1д	±С ₂ = ±D ₂	[2,2 ⁺ ] [2 ⁺ ,2]		4	Я ₄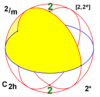

Международный	Гео	Орбифолд	Шёнфлис	Конвей	Коксетер	Заказ	Абстрактный
2 3 4 5 6 н	2 3 4 5 6 н	22 33 44 55 66 нн	С ₂ С ₃ С ₄ С ₅ С ₆ С _н	С ₂ С ₃ С ₄ С ₅ С ₆ С _н	[2] ⁺ [3] ⁺ [4] ⁺ [5] ⁺ [6] ⁺ [н] ⁺	2 3 4 5 6 н	Z ₂ Z ₃ Z ₄ Z ₅ Z ₆ Z _н
2мм 3м 4мм 5м 6мм нм (n нечетное) нмм (n четное)	2 3 4 5 6 н	22 33 44 55 66 нн	С _2в С _3в С _4в С _5в С _6в С _нв	КД ₄ КД ₆ КД ₈ КД ₁₀ КД ₁₂ КД _2n	[2] [3] [4] [5] [6] [сущ.]	4 6 8 10 12 2н	Д ₄ Д ₆ Д ₈ Д ₁₀ Д ₁₂ Д _{2 н}
3 8 5 12 -	62 82 10,2 12,2 2н.2	3× 4× 5× 6× n×	С ₆ С ₈ С ₁₀ С ₁₂ С _2н	±С ₃ СС ₈ ±С ₅ СС ₁₂ СС _2н / ±С _н	[2 ⁺ ,6 ⁺ ] [2 ⁺ ,8 ⁺ ] [2 ⁺ ,10 ⁺ ] [2 ⁺ ,12 ⁺ ] [2 ⁺ ,2 n ⁺ ]	6 8 10 12 2н	Я ₆ Я ₈ Я ₁₀ Я ₁₂ Я _{2 н}
3/м= 6 4/м 5/м= 10 6/м н/м	3 2 4 2 5 2 6 2 н 2	3* 4* 5* 6* н*	С _3ч С _4ч С _5ч С _6ч С _нч	CC ₆ ±C ₄ CC ₁₀ ±C ₆ ±C _n / CC _2n	[2,3 ⁺ ] [2,4 ⁺ ] [2,5 ⁺ ] [2,6 ⁺ ] [2,n ⁺ ]	6 8 10 12 2н	Z ₆ Z ₂ ×Z ₄ Z ₁₀ Z ₂ ×Z ₆ Z ₂ ×Z _n ≅Z _{2 n} (нечетное n )

Диэдральная симметрия

Существует три бесконечных семейства диэдральной симметрии , где n = 2 или выше ( в частном случае n может быть равно 1).

Международный	Гео	Орбифолд	Шёнфлис	Конвей	Коксетер	Заказ	Абстрактный
222	2 . 2	222	Д ₂	Д ₄	[2,2] ⁺	4	Д ₄
4 2м	4 2	2*2	Д _2д	ДД ₈	[2 ⁺ ,4]	8	Д ₄
М-м-м	22	*222	Д _2ч	±D ₄	[2,2]	8	Z2 × _D4

Международный	Гео	Орбифолд	Шёнфлис	Конвей	Коксетер	Заказ	Абстрактный
32 422 52 622	3 . 2 4 . 2 5 . 2 6 . 2 н . 2	223 224 225 226 22н	Д ₃ Д ₄ Д ₅ Д ₆ Д _н	Д ₆ Д ₈ Д ₁₀ Д ₁₂ Д _2н	[2,3] ⁺ [2,4] ⁺ [2,5] ⁺ [2,6] ⁺ [2, н ] ⁺	6 8 10 12 2 н	Д ₆ Д ₈ Д ₁₀ Д ₁₂ Д _{2 н}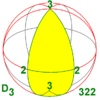
3 м 8 2м 5 м 12 .2м	6 2 8 2 10. 2 12. 2 н 2	23 24 25 26 2*н	Д _3д Д _4д Д _5д Д _6д Д _нд	±Д ₆ ДД ₁₆ ±Д ₁₀ ДД ₂₄ ДД _4n / ±Д _2n	[2 ⁺ ,6] [2 ⁺ ,8] [2 ⁺ ,10] [2 ⁺ ,12] [2 ⁺ ,2n]	12 16 20 24 4н	Д ₁₂ Д ₁₆ Д ₂₀ Д ₂₄ Д _{4 н}
6 м2 4/ммм 10 м2 6/ммм	32 42 52 62 н2	223 224 225 226 *22н	Д _3ч Д _4ч Д _5ч Д _6ч Д _нч	ДД ₁₂ ±Д ₈ ДД ₂₀ ±Д ₁₂ ±Д _2н / ДД _4н	[2,3] [2,4] [2,5] [2,6] [2,н]	12 16 20 24 4н	D ₁₂ Z ₂ ×D ₈ D ₂₀ Z ₂ ×D ₁₂ Z ₂ ×D _{2 n} ≅D _{4 n} (нечетное n )

Многогранная симметрия

Существует три типа полиэдральной симметрии : тетраэдрическая симметрия , октаэдрическая симметрия и икосаэдрическая симметрия , названные в честь правильных многогранников с треугольными гранями, обладающих этими симметриями.

Тетраэдрическая симметрия
Международный	Гео	Орбифолд	Шёнфлис	Конвей	Коксетер	Заказ	Абстрактный
23	3 . 3	332	Т	Т	[3,3] ⁺	12	А ₄
м 3	4 3	3*2	Т _ч	±Т	[4,3 ⁺ ]	24	2× А ₄
4 3м	33	*332	Т _д	К	[3,3]	24	С ₄

Октаэдрическая симметрия
Международный	Гео	Орбифолд	Шёнфлис	Конвей	Коксетер	Заказ	Абстрактный	Фонд. домен
432	4 . 3	432	О	О	[4,3] ⁺	24	С ₄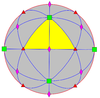
м 3 м	43	*432	Ой	±О	[4,3]	48	2× С ₄

Икосаэдрическая симметрия
Международный	Гео	Орбифолд	Шёнфлис	Конвей	Коксетер	Заказ	Абстрактный	Фонд. домен
532	5 . 3	532	я	я	[5,3] ⁺	60	А ₅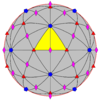
53 2/м	53	*532	Я _ч	±Я	[5,3]	120	2× А ₅

Непрерывные симметрии

Все дискретные точечные симметрии являются подгруппами определенных непрерывных симметрий. Их можно классифицировать как произведения ортогональных групп O( n ) или специальных ортогональных групп SO( n ). O(1) — это просто ортогональное отражение, двугранная симметрия порядка 2, Dih ₁ . SO(1) — это просто тождество. Для завершения необходимы полуобороты, C _{2 .}

Группы 3 ранга	Другие имена	Пример геометрии	Примеры конечных подгрупп
О(3)		Полная симметрия сферы	[3,3] =, [4,3] =, [5,3] = [4,3 ⁺ ] =
ТАК(3)	Группа сфер	Вращательная симметрия	[3,3] ⁺ =, [4,3] ⁺ =, [5,3] ⁺ =
О(2)×О(1) О(2)⋊С ₂	Dih _∞ ×Dih ₁ Dih _∞ ⋊C ₂	Полная симметрия сфероида , тора , цилиндра , биконуса или гиперболоида Полная круговая симметрия с полуоборотом	[ п ,2] = [ п ]×[ ] = [2 п ,2 ⁺ ] =, [2 п ⁺ ,2 ⁺ ] =
SO(2)×O(1)	С _∞ ×Dih ₁	Вращательная симметрия с отражением	[ п ⁺ ,2] = [ п ] ⁺ ×[ ] =
SO(2)⋊C ₂	С _∞ ⋊С ₂	Вращательная симметрия с полуоборотом	[ п ,2] ⁺ =
О(2)×SO(1)	Dih _∞ Круговая симметрия	Полная симметрия полусферы, конуса , параболоида или любой поверхности вращения	[ п ,1] = [ п ] =
SO(2)×SO(1)	C _∞ Круговая группа	Вращательная симметрия	[ п ,1] ⁺ = [ п ] ⁺ =

Смотрите также

Ссылки

^ Джонсон, 2015
^ Конвей, Джон Х. (2008). Симметрии вещей . Уэллсли, Массачусетс: AK Peters. ISBN 978-1-56881-220-5. OCLC 181862605.
^ Конвей, Джон; Смит, Дерек А. (2003). О кватернионах и октонионах: их геометрии, арифметике и симметрии . Натик, Массачусетс: AK Peters. ISBN 978-1-56881-134-5. OCLC 560284450.
^ Сэндс, «Введение в кристаллографию», 1993

Дальнейшее чтение

Питер Р. Кромвель, Многогранники (1997), Приложение I
Сэндс, Дональд Э. (1993). "Кристаллические системы и геометрия". Введение в кристаллографию . Минеола, Нью-Йорк: Dover Publications, Inc. стр. 165. ISBN 0-486-67839-3.
О кватернионах и октонионах , 2003, Джон Хортон Конвей и Дерек А. Смит ISBN 978-1-56881-134-5
Симметрии вещей 2008, Джон Х. Конвей, Хайди Бергиел, Хаим Гудман-Штраус, ISBN 978-1-56881-220-5
Калейдоскопы: избранные труды Х. С. М. Коксетера , под редакцией Ф. Артура Шерка, Питера МакМаллена, Энтони К. Томпсона, Азии Айвик Вайс, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [1]
- (Документ 22) HSM Coxeter, Правильные и полуправильные многогранники I , [Math. Zeit. 46 (1940) 380–407, MR 2,10]
- (Документ 23) HSM Коксетер, Правильные и полуправильные многогранники II , [Math. Zeit. 188 (1985) 559–591]
- (Документ 24) HSM Coxeter, Правильные и полуправильные многогранники III , [Math. Zeit. 200 (1988) 3–45]
NW Johnson : Геометрии и преобразования , (2018) ISBN 978-1-107-10340-5 Глава 11: Конечные группы симметрии , Таблица 11.4 Конечные группы изометрий в 3-пространстве

Внешние ссылки

Конечные сферические группы симметрии
Вайсштейн, Эрик В. «Символ Шенфлиса». Математический мир .
Вайсштейн, Эрик В. «Кристаллографические точечные группы». MathWorld .
Простейшие канонические многогранники каждого типа симметрии, Дэвид И. МакКуи

[1] Джонсон, 2015

[Conway_2008-2] Конвей, Джон Х. (2008). Симметрии вещей . Уэллсли, Массачусетс: AK Peters. ISBN 978-1-56881-220-5. OCLC 181862605.

[Conway_2003-3] Конвей, Джон; Смит, Дерек А. (2003). О кватернионах и октонионах: их геометрии, арифметике и симметрии . Натик, Массачусетс: AK Peters. ISBN 978-1-56881-134-5. OCLC 560284450.

[4] Сэндс, «Введение в кристаллографию», 1993