Распределение Пуассона

Распределение Пуассона

Функция массы вероятности 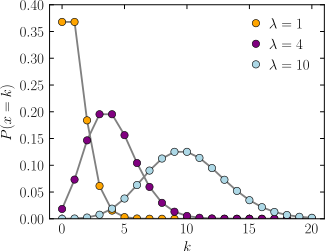Горизонтальная ось — индекс k , количество появлений. λ — ожидаемая частота появлений. Вертикальная ось — вероятность k появлений при заданном λ . Функция определена только при целых значениях k ; соединительные линии служат лишь ориентирами для глаза.
Кумулятивная функция распределения 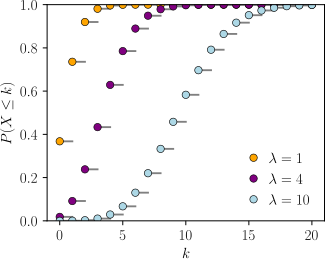Горизонтальная ось — это индекс k , количество вхождений. CDF разрывна в целых числах k и плоская везде, поскольку переменная, распределенная по закону Пуассона, принимает только целые значения.
Обозначение	${\displaystyle \operatorname {Pois} (\lambda )}$
Параметры	${\displaystyle \lambda \in (0,\infty )}$ (ставка)
Поддерживать	${\displaystyle k\in \mathbb {N} _{0}}$( Натуральные числа, начиная с 0)
ПМФ	${\displaystyle {\frac {\lambda ^{k}e^{-\lambda }}{k!}}}$
СДФ	${\displaystyle {\frac {\Gamma (\lfloor k+1\rfloor ,\lambda )}{\lfloor k\rfloor !}},}$или или${\displaystyle e^{-\lambda }\sum _{j=0}^{\lfloor k\rfloor }{\frac {\lambda ^{j}}{j!}},}$${\displaystyle Q(\lfloor k+1\rfloor ,\lambda )}$ ( где — верхняя неполная гамма-функция , — нижняя функция , а — регуляризованная гамма-функция )${\displaystyle k\geq 0,}$${\displaystyle \Gamma (x,y)}$${\displaystyle \lfloor k\rfloor }$${\displaystyle Q}$
Иметь в виду	${\displaystyle \lambda }$
Медиана	${\displaystyle \approx \left\lfloor \lambda +{\frac {1}{3}}-{\frac {1}{50\lambda }}\right\rfloor }$
Режим	${\displaystyle \left\lceil \lambda \right\rceil -1,\left\lfloor \lambda \right\rfloor }$
Дисперсия	${\displaystyle \lambda }$
Асимметрия	${\displaystyle {\frac {1}{\sqrt {\lambda }}}}$
Избыточный эксцесс	${\displaystyle {\frac {1}{\lambda }}}$
Энтропия	${\displaystyle \lambda {\Bigl [}1-\log(\lambda ){\Bigr ]}+e^{-\lambda }\sum _{k=0}^{\infty }{\frac {\lambda ^{k}\log(k!)}{k!}}}$  или для больших${\displaystyle \lambda }$   ${\displaystyle {\begin{aligned}\approx {\frac {1}{2}}\log \left(2\pi e\lambda \right)-{\frac {1}{12\lambda }}-{\frac {1}{24\lambda ^{2}}}\\-{\frac {19}{360\lambda ^{3}}}+{\mathcal {O}}\left({\frac {1}{\lambda ^{4}}}\right)\end{aligned}}}$
МГФ	${\displaystyle \exp \left[\lambda \left(e^{t}-1\right)\right]}$
CF	${\displaystyle \exp \left[\lambda \left(e^{it}-1\right)\right]}$
ПГФ	${\displaystyle \exp \left[\lambda \left(z-1\right)\right]}$
Информация о Фишере	${\displaystyle {\frac {1}{\lambda }}}$

В теории вероятностей и статистике распределение Пуассона ( / ˈ p w ɑː s ɒ n / ) — это дискретное распределение вероятностей , которое выражает вероятность заданного числа событий, происходящих в фиксированном интервале времени, если эти события происходят с известной постоянной средней скоростью и независимо от времени, прошедшего с момента последнего события. ^[1] Его также можно использовать для числа событий в других типах интервалов, отличных от времени, и в размерности больше 1 (например, число событий в заданной области или объеме).

Распределение Пуассона названо в честь французского математика Симеона Дени Пуассона . Оно играет важную роль для дискретно-устойчивых распределений .

При распределении Пуассона с ожиданием λ событий в заданном интервале вероятность k событий в том же интервале равна: ^{[2] : 60}

${\displaystyle {\frac {\lambda ^{k}e^{-\lambda }}{k!}}.}$

Например, рассмотрим колл-центр, который получает в среднем λ = 3 звонка в минуту в любое время дня. Если звонки независимы, получение одного звонка не изменяет вероятность того, когда поступит следующий. При этих предположениях число звонков k , полученных в течение любой минуты, имеет распределение вероятности Пуассона. Получение k = от 1 до 4 звонков имеет вероятность около 0,77, в то время как получение 0 или по крайней мере 5 звонков имеет вероятность около 0,23.

Классическим примером, используемым для обоснования распределения Пуассона, является число событий радиоактивного распада в течение фиксированного периода наблюдения. ^[3]

Распределение было впервые введено Симеоном Дени Пуассоном (1781–1840) и опубликовано вместе с его теорией вероятностей в его работе Recherches sur la probabilité des jugements en matière criminelle et en matière civile (1837). ^{[4] : 205-207} Работа теоретизировала о количестве неправомерных осуждений в данной стране, сосредоточившись на определенных случайных величинах N , которые подсчитывают, среди прочего, количество дискретных событий (иногда называемых «событиями» или «прибытиями»), которые происходят в течение временного интервала заданной длины. Результат уже был дан в 1711 году Авраамом де Муавром в De Mensura Sortis seu; de Probabilitate Eventuum in Ludis a Casu Fortuito Pendentibus . ^{[5] : 219  [6] : 14-15  [7] : 193  [8] : 157} Это делает его примером закона Стиглера и побудило некоторых авторов утверждать, что распределение Пуассона должно носить имя Муавра. ^{[9] [10]}

В 1860 году Саймон Ньюкомб подогнал распределение Пуассона к числу звезд, обнаруженных в единице пространства. ^[11] Дальнейшее практическое применение было сделано Ладиславом Борткевичем в 1898 году. Борткевич показал, что частота, с которой солдаты прусской армии случайно погибали от ударов лошади, может быть хорошо смоделирована с помощью распределения Пуассона. ^{[12] : 23-25} ​​.

Говорят, что дискретная случайная величина X имеет распределение Пуассона с параметром , если ее функция массы вероятности задается следующим образом: ^{[2] : 60}${\displaystyle \lambda >0}$

${\displaystyle f(k;\lambda )=\Pr(X{=}k)={\frac {\lambda ^{k}e^{-\lambda }}{k!}},}$

где

• k — количество появлений ( )${\displaystyle k=0,1,2,\ldots }$
• e — число Эйлера ( )${\displaystyle e=2.71828\ldots }$
• k ! = k ( k– 1) ··· (3)(2)(1) — факториал .

Положительное действительное число λ равно ожидаемому значению X , а также его дисперсии . ^[13]

${\displaystyle \lambda =\operatorname {E} (X)=\operatorname {Var} (X).}$

Распределение Пуассона может быть применено к системам с большим числом возможных событий, каждое из которых является редким . Число таких событий, которые происходят в течение фиксированного интервала времени, при правильных обстоятельствах является случайным числом с распределением Пуассона.

Уравнение можно адаптировать, если вместо среднего числа событий нам дана средняя скорость , с которой происходят события. Тогда и: ^[14]${\displaystyle \lambda ,}$${\displaystyle r}$${\displaystyle \lambda =rt,}$

${\displaystyle P(k{\text{ events in interval }}t)={\frac {(rt)^{k}e^{-rt}}{k!}}.}$

Распределение Пуассона может быть полезно для моделирования таких событий, как:

• количество метеоритов диаметром более 1 метра, падающих на Землю за год;
• количество лазерных фотонов, попадающих на детектор за определенный промежуток времени;
• количество студентов, получивших низкую и высокую оценку на экзамене; и
• места дефектов и дислокаций в материалах.

Примерами появления случайных точек в пространстве являются: места падения астероидов на Землю (двумерные), места дефектов в материале (трехмерные) и места расположения деревьев в лесу (двумерные). ^[15]

Распределение Пуассона является подходящей моделью, если верны следующие предположения:

• k — неотрицательное целое число, представляющее собой количество раз, когда событие происходит в течение интервала.
• Наступление одного события не влияет на вероятность наступления второго события.
• Средняя скорость, с которой происходят события, не зависит от каких-либо происшествий.
• Два события не могут произойти в один и тот же момент.

Если эти условия верны, то k является пуассоновской случайной величиной; распределение k является распределением Пуассона.

Распределение Пуассона также является пределом биномиального распределения , для которого вероятность успеха для каждой попытки равна λ, деленной на число попыток, поскольку число попыток стремится к бесконечности (см. Связанные распределения).

Предположим, что астрономы подсчитали, что крупные метеориты (больше определенного размера) падают на Землю в среднем раз в 100 лет ( λ = 1 событие за 100 лет), и что количество падений метеоритов следует распределению Пуассона. Какова вероятность k = 0 падений метеоритов в течение следующих 100 лет?

${\displaystyle P(k={\text{0 meteorites hit in next 100 years}})={\frac {1^{0}e^{-1}}{0!}}={\frac {1}{e}}\approx 0.37.}$

При этих предположениях вероятность того, что в течение следующих 100 лет на Землю не упадет ни одного крупного метеорита, составляет примерно 0,37. Оставшиеся 1 − 0,37 = 0,63 представляют собой вероятность падения 1, 2, 3 или более крупных метеоритов в течение следующих 100 лет. В приведенном выше примере наводнение из-за разлива происходило раз в 100 лет ( λ = 1). Вероятность отсутствия наводнений из-за разлива в течение 100 лет составила примерно 0,37 по тем же расчетам.

В общем, если событие происходит в среднем один раз за интервал ( λ  = 1), и события следуют распределению Пуассона, то P (0 событий в следующем интервале) = 0,37. Кроме того, P (ровно одно событие в следующем интервале) = 0,37, как показано в таблице для паводков.

Число студентов, прибывающих в студенческий союз в минуту, скорее всего, не будет подчиняться распределению Пуассона, поскольку скорость не является постоянной (низкая скорость во время занятий, высокая скорость между занятиями), а прибытие отдельных студентов не является независимым (студенты, как правило, приходят группами). Непостоянная скорость прибытия может быть смоделирована как смешанное распределение Пуассона , а прибытие групп, а не отдельных студентов, как сложный процесс Пуассона .

Число землетрясений магнитудой 5 в год в стране может не подчиняться распределению Пуассона, если одно крупное землетрясение увеличивает вероятность повторных толчков аналогичной магнитуды.

Примеры, в которых гарантировано хотя бы одно событие, не распределены по закону Пуассона, но могут быть смоделированы с использованием усеченного до нуля распределения Пуассона .

Распределения количества, в которых число интервалов с нулевыми событиями выше, чем предсказывает модель Пуассона, можно смоделировать с помощью модели с завышением нуля .

• Ожидаемое значение случайной величины Пуассона равно λ .
• Дисперсия случайной величины Пуассона также равна λ .
• Коэффициент вариации равен , а индекс дисперсии равен 1. ^{[8] : 163}${\textstyle \lambda ^{-1/2},}$
• Среднее абсолютное отклонение от среднего составляет ^{[8] : 163} $${\displaystyle \operatorname {E} [\ |X-\lambda |\ ]={\frac {2\lambda ^{\lfloor \lambda \rfloor +1}e^{-\lambda }}{\lfloor \lambda \rfloor !}}.}$$
• Мода случайной величины , распределенной по Пуассону, с нецелым λ равна наибольшему целому числу, меньшему или равному  λ . Это также записывается как floor ( λ ). Когда λ — положительное целое число, моды равны λ и λ  − 1.${\displaystyle \lfloor \lambda \rfloor ,}$
• Все кумулянты распределения Пуассона равны ожидаемому значению  λ .  Факториальный момент n распределения Пуассона равен λ ⁿ  .
• Ожидаемое значение процесса Пуассона иногда разлагается на произведение интенсивности и экспозиции (или, в более общем смысле, выражается как интеграл «функции интенсивности» по времени или пространству, иногда описываемый как «экспозиция»). ^[17]

Границы для медианы ( ) распределения известны и являются точными : ^[18]${\displaystyle \nu }$$${\displaystyle \lambda -\ln 2\leq \nu <\lambda +{\frac {1}{3}}.}$$

Высшие нецентрированные моменты m _k распределения Пуассона являются полиномами Тушара по λ : где фигурные скобки { } обозначают числа Стирлинга второго рода . ^{[19] [1] : 6} Другими словами, когда ожидаемое значение установлено равным λ = 1, формула Добински подразумевает, что n -й момент равен числу разбиений множества размера n .$${\displaystyle m_{k}=\sum _{i=0}^{k}\lambda ^{i}{\begin{Bmatrix}k\\i\end{Bmatrix}},}$$$${\displaystyle E[X]=\lambda ,\quad E[X(X-1)]=\lambda ^{2},\quad E[X(X-1)(X-2)]=\lambda ^{3},\cdots }$$

Простая верхняя граница: ^[20]$${\displaystyle m_{k}=E[X^{k}]\leq \left({\frac {k}{\log(k/\lambda +1)}}\right)^{k}\leq \lambda ^{k}\exp \left({\frac {k^{2}}{2\lambda }}\right).}$$

Если для независимы , то ^{[21] : 65} Обратной теоремой является теорема Райкова , которая гласит, что если сумма двух независимых случайных величин распределена по закону Пуассона, то таковыми являются и каждая из этих двух независимых случайных величин. ^{[22] [23]}${\displaystyle X_{i}\sim \operatorname {Pois} (\lambda _{i})}$${\displaystyle i=1,\dotsc ,n}$${\textstyle \sum _{i=1}^{n}X_{i}\sim \operatorname {Pois} \left(\sum _{i=1}^{n}\lambda _{i}\right).}$

Это распределение с максимальной энтропией среди множества обобщенных биномиальных распределений со средним значением и , ^[24] где обобщенное биномиальное распределение определяется как распределение суммы N независимых, но не одинаково распределенных переменных Бернулли.${\displaystyle B_{n}(\lambda )}$${\displaystyle \lambda }$${\displaystyle n\rightarrow \infty }$

• Распределения Пуассона являются бесконечно делимыми распределениями вероятностей. ^{[25] : 233  [8] : 164}
• Направленное расхождение Кульбака–Лейблера от определяется выражением${\displaystyle P=\operatorname {Pois} (\lambda )}$${\displaystyle P_{0}=\operatorname {Pois} (\lambda _{0})}$$${\displaystyle \operatorname {D} _{\text{KL}}(P\parallel P_{0})=\lambda _{0}-\lambda +\lambda \log {\frac {\lambda }{\lambda _{0}}}.}$$
• Если — целое число, то удовлетворяет и ^{[26] [ проверка не пройдена — см. обсуждение ]}${\displaystyle \lambda \geq 1}$${\displaystyle Y\sim \operatorname {Pois} (\lambda )}$${\displaystyle \Pr(Y\geq E[Y])\geq {\frac {1}{2}}}$${\displaystyle \Pr(Y\leq E[Y])\geq {\frac {1}{2}}.}$
• Границы для хвостовых вероятностей случайной величины Пуассона можно вывести с использованием аргумента границы Чернова . ^{[27] : 97-98}${\displaystyle X\sim \operatorname {Pois} (\lambda )}$ $${\displaystyle P(X\geq x)\leq {\frac {(e\lambda )^{x}e^{-\lambda }}{x^{x}}},{\text{ for }}x>\lambda ,}$$ $${\displaystyle P(X\leq x)\leq {\frac {(e\lambda )^{x}e^{-\lambda }}{x^{x}}},{\text{ for }}x<\lambda .}$$
• Вероятность верхнего хвоста может быть сужена (по крайней мере, в два раза) следующим образом: ^[28]

$${\displaystyle P(X\geq x)\leq {\frac {e^{-\operatorname {D} _{\text{KL}}(Q\parallel P)}}{\max {(2,{\sqrt {4\pi \operatorname {D} _{\text{KL}}(Q\parallel P)}}})}},{\text{ for }}x>\lambda ,}$$где — расхождение Кульбака–Лейблера от .${\displaystyle \operatorname {D} _{\text{KL}}(Q\parallel P)}$${\displaystyle Q=\operatorname {Pois} (x)}$${\displaystyle P=\operatorname {Pois} (\lambda )}$

• Неравенства, связывающие функцию распределения случайной величины Пуассона со стандартной нормальной функцией распределения , следующие: ^[29] где — расхождение Кульбака–Лейблера от , а — расхождение Кульбака–Лейблера от .${\displaystyle X\sim \operatorname {Pois} (\lambda )}$${\displaystyle \Phi (x)}$ $${\displaystyle \Phi \left(\operatorname {sign} (k-\lambda ){\sqrt {2\operatorname {D} _{\text{KL}}(Q_{-}\parallel P)}}\right)<P(X\leq k)<\Phi \left(\operatorname {sign} (k+1-\lambda ){\sqrt {2\operatorname {D} _{\text{KL}}(Q_{+}\parallel P)}}\right),{\text{ for }}k>0,}$$${\displaystyle \operatorname {D} _{\text{KL}}(Q_{-}\parallel P)}$${\displaystyle Q_{-}=\operatorname {Pois} (k)}$${\displaystyle P=\operatorname {Pois} (\lambda )}$${\displaystyle \operatorname {D} _{\text{KL}}(Q_{+}\parallel P)}$${\displaystyle Q_{+}=\operatorname {Pois} (k+1)}$${\displaystyle P}$

Пусть и — независимые случайные величины, тогда имеем, что${\displaystyle X\sim \operatorname {Pois} (\lambda )}$${\displaystyle Y\sim \operatorname {Pois} (\mu )}$${\displaystyle \lambda <\mu ,}$$${\displaystyle {\frac {e^{-({\sqrt {\mu }}-{\sqrt {\lambda }})^{2}}}{(\lambda +\mu )^{2}}}-{\frac {e^{-(\lambda +\mu )}}{2{\sqrt {\lambda \mu }}}}-{\frac {e^{-(\lambda +\mu )}}{4\lambda \mu }}\leq P(X-Y\geq 0)\leq e^{-({\sqrt {\mu }}-{\sqrt {\lambda }})^{2}}}$$

Верхняя граница доказана с использованием стандартной границы Чернова.

Нижнюю границу можно доказать, заметив, что есть вероятность того, что где , которая ограничена снизу где есть относительная энтропия (см. статью о границах хвостов биномиальных распределений для получения подробной информации). Далее отметив, что и вычислив нижнюю границу безусловной вероятности, получаем результат. Более подробную информацию можно найти в приложении к Kamath et al. ^[30]${\displaystyle P(X-Y\geq 0\mid X+Y=i)}$${\textstyle Z\geq {\frac {i}{2}},}$${\textstyle Z\sim \operatorname {Bin} \left(i,{\frac {\lambda }{\lambda +\mu }}\right),}$${\textstyle {\frac {1}{(i+1)^{2}}}e^{-iD\left(0.5\|{\frac {\lambda }{\lambda +\mu }}\right)},}$${\displaystyle D}$${\displaystyle X+Y\sim \operatorname {Pois} (\lambda +\mu ),}$

Распределение Пуассона может быть получено как предельный случай биномиального распределения , когда число попыток стремится к бесконечности, а ожидаемое число успехов остается фиксированным — см. закон редких событий ниже. Следовательно, его можно использовать в качестве приближения биномиального распределения, если n достаточно велико, а p достаточно мало. Распределение Пуассона является хорошим приближением биномиального распределения, если n не менее 20, а p меньше или равно 0,05, и превосходным приближением, если n  ≥ 100 и np  ≤ 10. ^[31] Позволяя и быть соответствующими функциями кумулятивной плотности биномиального и пуассоновского распределений, имеем: Один вывод этого использует функции генерации вероятности . ^[32] Рассмотрим испытание Бернулли (подбрасывание монеты), вероятность одного успеха (или ожидаемое число успехов) которого находится в пределах заданного интервала. Разбейте интервал на n частей и выполните испытание в каждом подынтервале с вероятностью . Вероятность k успехов из n попыток на всем интервале затем определяется биномиальным распределением${\displaystyle F_{\mathrm {B} }}$${\displaystyle F_{\mathrm {P} }}$$${\displaystyle F_{\mathrm {B} }(k;n,p)\ \approx \ F_{\mathrm {P} }(k;\lambda =np).}$$${\displaystyle \lambda \leq 1}$${\displaystyle {\tfrac {\lambda }{n}}}$

${\displaystyle p_{k}^{(n)}={\binom {n}{k}}\left({\frac {\lambda }{n}}\right)^{\!k}\left(1{-}{\frac {\lambda }{n}}\right)^{\!n-k},}$

производящая функция которой:

${\displaystyle P^{(n)}(x)=\sum _{k=0}^{n}p_{k}^{(n)}x^{k}=\left(1-{\frac {\lambda }{n}}+{\frac {\lambda }{n}}x\right)^{n}.}$

Принимая предел при увеличении n до бесконечности (при фиксированном x ) и применяя определение предела произведения экспоненциальной функции , это сводится к производящей функции распределения Пуассона:

${\displaystyle \lim _{n\to \infty }P^{(n)}(x)=\lim _{n\to \infty }\left(1{+}{\tfrac {\lambda (x-1)}{n}}\right)^{n}=e^{\lambda (x-1)}=\sum _{k=0}^{\infty }e^{-\lambda }{\frac {\lambda ^{k}}{k!}}x^{k}.}$

• Если и независимы, то разность следует распределению Скеллама .${\displaystyle X_{1}\sim \mathrm {Pois} (\lambda _{1})\,}$${\displaystyle X_{2}\sim \mathrm {Pois} (\lambda _{2})\,}$${\displaystyle Y=X_{1}-X_{2}}$
• Если и независимы, то распределение условного значения является биномиальным .${\displaystyle X_{1}\sim \mathrm {Pois} (\lambda _{1})\,}$${\displaystyle X_{2}\sim \mathrm {Pois} (\lambda _{2})\,}$${\displaystyle X_{1}}$${\displaystyle X_{1}+X_{2}}$
  В частности, если тогда${\displaystyle X_{1}+X_{2}=k,}$${\displaystyle X_{1}|X_{1}+X_{2}=k\sim \mathrm {Binom} (k,\lambda _{1}/(\lambda _{1}+\lambda _{2})).}$
  В более общем случае, если X ₁ , X ₂ , ..., X _n являются независимыми случайными величинами Пуассона с параметрами λ ₁ , λ ₂ , ..., λ _{n ,} то

  учитывая , что следует, что на самом деле,${\displaystyle \sum _{j=1}^{n}X_{j}=k,}$${\displaystyle X_{i}{\Big |}\sum _{j=1}^{n}X_{j}=k\sim \mathrm {Binom} \left(k,{\frac {\lambda _{i}}{\sum _{j=1}^{n}\lambda _{j}}}\right).}$${\displaystyle \{X_{i}\}\sim \mathrm {Multinom} \left(k,\left\{{\frac {\lambda _{i}}{\sum _{j=1}^{n}\lambda _{j}}}\right\}\right).}$

• Если и распределение условного на X  =  k является биномиальным распределением , то распределение Y следует распределению Пуассона. Фактически, если условное на следует полиномиальному распределению , то каждое следует независимому распределению Пуассона.${\displaystyle X\sim \mathrm {Pois} (\lambda )\,}$${\displaystyle Y}$${\displaystyle Y\mid (X=k)\sim \mathrm {Binom} (k,p),}$${\displaystyle Y\sim \mathrm {Pois} (\lambda \cdot p).}$${\displaystyle \{X=k\},}$ ${\displaystyle \{Y_{i}\}}$${\displaystyle \{Y_{i}\}\mid (X=k)\sim \mathrm {Multinom} \left(k,p_{i}\right),}$${\displaystyle Y_{i}}$${\displaystyle Y_{i}\sim \mathrm {Pois} (\lambda \cdot p_{i}),\rho (Y_{i},Y_{j})=0.}$
• Распределение Пуассона является частным случаем дискретного составного распределения Пуассона (или прерывистого распределения Пуассона) только с одним параметром. ^{[33] [34]} Дискретное составное распределение Пуассона может быть выведено из предельного распределения одномерного полиномиального распределения. Это также частный случай составного распределения Пуассона .
• Для достаточно больших значений λ (скажем, λ >1000) нормальное распределение со средним λ и дисперсией λ (стандартное отклонение ) является отличным приближением к распределению Пуассона. Если λ больше примерно 10, то нормальное распределение является хорошим приближением, если выполняется соответствующая коррекция непрерывности , т. е. если P( X ≤ x ) , где x — неотрицательное целое число, заменяется на P( X ≤ x + 0,5) .${\displaystyle {\sqrt {\lambda }}}$$${\displaystyle F_{\mathrm {Poisson} }(x;\lambda )\approx F_{\mathrm {normal} }(x;\mu =\lambda ,\sigma ^{2}=\lambda )}$$
• Преобразование, стабилизирующее дисперсию : Если то ^{[8] : 168} и ^{[35] : 196} При этом преобразовании сходимость к нормальности (при увеличении) происходит гораздо быстрее, чем для непреобразованной переменной. ^{[ необходима ссылка ]} Доступны и другие, немного более сложные преобразования, стабилизирующие дисперсию, ^{[8] : 168} одним из которых является преобразование Анскомба . ^[36] См. Преобразование данных (статистика) для более общего использования преобразований.${\displaystyle X\sim \mathrm {Pois} (\lambda ),}$ $${\displaystyle Y=2{\sqrt {X}}\approx {\mathcal {N}}(2{\sqrt {\lambda }};1),}$$ $${\displaystyle Y={\sqrt {X}}\approx {\mathcal {N}}({\sqrt {\lambda }};1/4).}$$${\displaystyle \lambda }$
• Если для каждого t  > 0 число прибытий в интервале времени [0, t ] следует распределению Пуассона со средним значением λt , то последовательность времен между прибытиями является независимыми и одинаково распределенными экспоненциальными случайными величинами со средним значением 1/ λ . ^{[37] : 317–319}
• Кумулятивные функции распределения Пуассона и хи-квадрат связаны следующим образом: ^{[8] : 167} и ^{[8] : 158}$${\displaystyle F_{\text{Poisson}}(k;\lambda )=1-F_{\chi ^{2}}(2\lambda ;2(k+1))\quad \quad {\text{ integer }}k,}$$ $${\displaystyle P(X=k)=F_{\chi ^{2}}(2\lambda ;2(k+1))-F_{\chi ^{2}}(2\lambda ;2k).}$$

Предположим , что где тогда ^[38] распределено мультиномиально при условии${\displaystyle X_{1}\sim \operatorname {Pois} (\lambda _{1}),X_{2}\sim \operatorname {Pois} (\lambda _{2}),\dots ,X_{n}\sim \operatorname {Pois} (\lambda _{n})}$${\displaystyle \lambda _{1}+\lambda _{2}+\dots +\lambda _{n}=1,}$ ${\displaystyle (X_{1},X_{2},\dots ,X_{n})}$${\displaystyle (X_{1},X_{2},\dots ,X_{n})\sim \operatorname {Mult} (N,\lambda _{1},\lambda _{2},\dots ,\lambda _{n})}$${\displaystyle N=X_{1}+X_{2}+\dots X_{n}.}$

Это означает ^{[27] : 101-102} , среди прочего, что для любой неотрицательной функции, если она распределена мультиномиально, то где${\displaystyle f(x_{1},x_{2},\dots ,x_{n}),}$${\displaystyle (Y_{1},Y_{2},\dots ,Y_{n})\sim \operatorname {Mult} (m,\mathbf {p} )}$$${\displaystyle \operatorname {E} [f(Y_{1},Y_{2},\dots ,Y_{n})]\leq e{\sqrt {m}}\operatorname {E} [f(X_{1},X_{2},\dots ,X_{n})]}$$${\displaystyle (X_{1},X_{2},\dots ,X_{n})\sim \operatorname {Pois} (\mathbf {p} ).}$

Множитель можно заменить на 2, если дополнительно предположить, что он монотонно возрастает или убывает.${\displaystyle e{\sqrt {m}}}$${\displaystyle f}$

Это распределение было распространено на двумерный случай. ^[39] Производящая функция для этого распределения имеет вид$${\displaystyle g(u,v)=\exp[(\theta _{1}-\theta _{12})(u-1)+(\theta _{2}-\theta _{12})(v-1)+\theta _{12}(uv-1)]}$$

с$${\displaystyle \theta _{1},\theta _{2}>\theta _{12}>0}$$

Предельные распределения — это распределения Пуассона ( θ ₁ ) и Пуассона ( θ ₂ ), а коэффициент корреляции ограничен диапазоном$${\displaystyle 0\leq \rho \leq \min \left\{{\sqrt {\frac {\theta _{1}}{\theta _{2}}}},{\sqrt {\frac {\theta _{2}}{\theta _{1}}}}\right\}}$$

Простой способ создания двумерного распределения Пуассона — взять три независимых распределения Пуассона со средними значениями , а затем задать Вероятностную функцию двумерного распределения Пуассона:${\displaystyle X_{1},X_{2}}$${\displaystyle Y_{1},Y_{2},Y_{3}}$${\displaystyle \lambda _{1},\lambda _{2},\lambda _{3}}$${\displaystyle X_{1}=Y_{1}+Y_{3},X_{2}=Y_{2}+Y_{3}.}$$${\displaystyle \Pr(X_{1}=k_{1},X_{2}=k_{2})=\exp \left(-\lambda _{1}-\lambda _{2}-\lambda _{3}\right){\frac {\lambda _{1}^{k_{1}}}{k_{1}!}}{\frac {\lambda _{2}^{k_{2}}}{k_{2}!}}\sum _{k=0}^{\min(k_{1},k_{2})}{\binom {k_{1}}{k}}{\binom {k_{2}}{k}}k!\left({\frac {\lambda _{3}}{\lambda _{1}\lambda _{2}}}\right)^{k}}$$

Свободное распределение Пуассона ^[40] с размером и скоростью скачка возникает в свободной теории вероятностей как предел повторной свободной свертки при N → ∞ .${\displaystyle \alpha }$${\displaystyle \lambda }$$${\displaystyle \left(\left(1-{\frac {\lambda }{N}}\right)\delta _{0}+{\frac {\lambda }{N}}\delta _{\alpha }\right)^{\boxplus N}}$$

Другими словами, пусть будут случайными величинами, так что имеет значение с вероятностью и значение 0 с оставшейся вероятностью. Предположим также, что семейство свободно независимо . Тогда предел по закону задается свободным законом Пуассона с параметрами${\displaystyle X_{N}}$${\displaystyle X_{N}}$${\displaystyle \alpha }$${\textstyle {\frac {\lambda }{N}}}$${\displaystyle X_{1},X_{2},\ldots }$${\displaystyle N\to \infty }$${\displaystyle X_{1}+\cdots +X_{N}}$${\displaystyle \lambda ,\alpha .}$

Это определение аналогично одному из способов, с помощью которого классическое распределение Пуассона получается из (классического) процесса Пуассона.

Мера, связанная со свободным законом Пуассона, определяется выражением ^[41] , где и имеет поддержку$${\displaystyle \mu ={\begin{cases}(1-\lambda )\delta _{0}+\nu ,&{\text{if }}0\leq \lambda \leq 1\\\nu ,&{\text{if }}\lambda >1,\end{cases}}}$$$${\displaystyle \nu ={\frac {1}{2\pi \alpha t}}{\sqrt {4\lambda \alpha ^{2}-(t-\alpha (1+\lambda ))^{2}}}\,dt}$$${\displaystyle [\alpha (1-{\sqrt {\lambda }})^{2},\alpha (1+{\sqrt {\lambda }})^{2}].}$

Этот закон также возникает в теории случайных матриц как закон Марченко–Пастура . Его свободные кумулянты равны${\displaystyle \kappa _{n}=\lambda \alpha ^{n}.}$

Мы приводим значения некоторых важных преобразований свободного закона Пуассона; вычисление можно найти, например, в книге « Лекции по комбинаторике свободной вероятности» А. Ники и Р. Шпайхера ^[42].

R-преобразование свободного закона Пуассона определяется выражением$${\displaystyle R(z)={\frac {\lambda \alpha }{1-\alpha z}}.}$$

Преобразование Коши (которое является отрицательным преобразованием Стилтьеса ) определяется выражением$${\displaystyle G(z)={\frac {z+\alpha -\lambda \alpha -{\sqrt {(z-\alpha (1+\lambda ))^{2}-4\lambda \alpha ^{2}}}}{2\alpha z}}}$$

S-преобразование задается в случае, если$${\displaystyle S(z)={\frac {1}{z+\lambda }}}$$${\displaystyle \alpha =1.}$

Функция массы вероятности Пуассона может быть выражена в форме, аналогичной распределению произведения распределения Вейбулла и варианту формы устойчивого распределения счета . Переменная может рассматриваться как обратная параметру устойчивости Леви в устойчивом распределении счета: где — стандартное устойчивое распределение счета формы , а — стандартное распределение Вейбулла формы${\displaystyle f(k;\lambda )}$${\displaystyle (k+1)}$$${\displaystyle f(k;\lambda )=\int _{0}^{\infty }{\frac {1}{u}}\,W_{k+1}\left({\frac {\lambda }{u}}\right)\left[(k+1)u^{k}\,{\mathfrak {N}}_{\frac {1}{k+1}}(u^{k+1})\right]\,du,}$$${\displaystyle {\mathfrak {N}}_{\alpha }(\nu )}$${\displaystyle \alpha =1/(k+1),}$${\displaystyle W_{k+1}(x)}$${\displaystyle k+1.}$

Учитывая выборку из n измеренных значений для i = 1, ..., n , мы хотим оценить значение параметра λ пуассоновской популяции, из которой была взята выборка. Оценка максимального правдоподобия равна ^[43]${\displaystyle k_{i}\in \{0,1,\dots \},}$

${\displaystyle {\widehat {\lambda }}_{\mathrm {MLE} }={\frac {1}{n}}\sum _{i=1}^{n}k_{i}\ .}$

Поскольку каждое наблюдение имеет ожидание λ, то же самое относится и к выборочному среднему. Следовательно, оценка максимального правдоподобия является несмещенной оценкой λ . Она также является эффективной оценкой, поскольку ее дисперсия достигает нижней границы Крамера–Рао (CRLB). ^[44] Следовательно, она является несмещенной с минимальной дисперсией . Также можно доказать, что сумма (и, следовательно, выборочное среднее, поскольку оно является функцией суммы один к одному) является полной и достаточной статистикой для λ .

Для доказательства достаточности можно использовать теорему о факторизации . Рассмотрим разбиение функции массы вероятности совместного распределения Пуассона для выборки на две части: одну, которая зависит исключительно от выборки , называемую , и другую, которая зависит от параметра и выборки только через функцию Тогда является достаточной статистикой для${\displaystyle \mathbf {x} }$${\displaystyle h(\mathbf {x} )}$${\displaystyle \lambda }$${\displaystyle \mathbf {x} }$${\displaystyle T(\mathbf {x} ).}$${\displaystyle T(\mathbf {x} )}$${\displaystyle \lambda .}$

${\displaystyle P(\mathbf {x} )=\prod _{i=1}^{n}{\frac {\lambda ^{x_{i}}e^{-\lambda }}{x_{i}!}}={\frac {1}{\prod _{i=1}^{n}x_{i}!}}\times \lambda ^{\sum _{i=1}^{n}x_{i}}e^{-n\lambda }}$

Первый член зависит только от . Второй член зависит от выборки только через Таким образом, достаточно.${\displaystyle h(\mathbf {x} )}$${\displaystyle \mathbf {x} }$${\displaystyle g(T(\mathbf {x} )|\lambda )}$${\textstyle T(\mathbf {x} )=\sum _{i=1}^{n}x_{i}.}$${\displaystyle T(\mathbf {x} )}$

Чтобы найти параметр λ , который максимизирует функцию вероятности для популяции Пуассона, мы можем использовать логарифм функции правдоподобия:

${\displaystyle {\begin{aligned}\ell (\lambda )&=\ln \prod _{i=1}^{n}f(k_{i}\mid \lambda )\\&=\sum _{i=1}^{n}\ln \!\left({\frac {e^{-\lambda }\lambda ^{k_{i}}}{k_{i}!}}\right)\\&=-n\lambda +\left(\sum _{i=1}^{n}k_{i}\right)\ln(\lambda )-\sum _{i=1}^{n}\ln(k_{i}!).\end{aligned}}}$

Берем производную по λ и сравниваем ее с нулем:${\displaystyle \ell }$

${\displaystyle {\frac {\mathrm {d} }{\mathrm {d} \lambda }}\ell (\lambda )=0\iff -n+\left(\sum _{i=1}^{n}k_{i}\right){\frac {1}{\lambda }}=0.\!}$

Решение относительно λ дает стационарную точку.

${\displaystyle \lambda ={\frac {\sum _{i=1}^{n}k_{i}}{n}}}$

Итак, λ — это среднее значение k _i . Получение знака второй производной L в стационарной точке определит, каким экстремальным значением является λ .

${\displaystyle {\frac {\partial ^{2}\ell }{\partial \lambda ^{2}}}=-\lambda ^{-2}\sum _{i=1}^{n}k_{i}}$

Оценка второй производной в стационарной точке дает:

${\displaystyle {\frac {\partial ^{2}\ell }{\partial \lambda ^{2}}}=-{\frac {n^{2}}{\sum _{i=1}^{n}k_{i}}}}$

что является отрицательным значением n , умноженным на обратную величину среднего значения k _i . Это выражение отрицательно, когда среднее значение положительно. Если это выполняется, то стационарная точка максимизирует функцию вероятности.

Для полноты семейство распределений называется полным тогда и только тогда, когда подразумевается, что для всех Если индивидуумы являются независимыми , то Зная распределение, которое мы хотим исследовать, легко видеть, что статистика является полной.${\displaystyle E(g(T))=0}$${\displaystyle P_{\lambda }(g(T)=0)=1}$${\displaystyle \lambda .}$${\displaystyle X_{i}}$${\displaystyle \mathrm {Po} (\lambda ),}$${\textstyle T(\mathbf {x} )=\sum _{i=1}^{n}X_{i}\sim \mathrm {Po} (n\lambda ).}$

${\displaystyle E(g(T))=\sum _{t=0}^{\infty }g(t){\frac {(n\lambda )^{t}e^{-n\lambda }}{t!}}=0}$

Для того чтобы это равенство выполнялось, должно быть равно 0. Это следует из того факта, что ни один из других членов не будет равен 0 для всех в сумме и для всех возможных значений Следовательно, для всех следует, что и было показано, что статистика является полной.${\displaystyle g(t)}$${\displaystyle t}$${\displaystyle \lambda .}$${\displaystyle E(g(T))=0}$${\displaystyle \lambda }$${\displaystyle P_{\lambda }(g(T)=0)=1,}$

Доверительный интервал для среднего значения распределения Пуассона может быть выражен с использованием соотношения между кумулятивными функциями распределения Пуассона и распределения хи-квадрат . Распределение хи-квадрат само по себе тесно связано с гамма-распределением , и это приводит к альтернативному выражению. При наличии наблюдения k из распределения Пуассона со средним значением μ доверительный интервал для μ с уровнем достоверности 1 – α равен

${\displaystyle {\tfrac {1}{2}}\chi ^{2}(\alpha /2;2k)\leq \mu \leq {\tfrac {1}{2}}\chi ^{2}(1-\alpha /2;2k+2),}$

или эквивалентно,

${\displaystyle F^{-1}(\alpha /2;k,1)\leq \mu \leq F^{-1}(1-\alpha /2;k+1,1),}$

где — квантильная функция (соответствующая нижней хвостовой области p ) распределения хи-квадрат с n степенями свободы, а — квантильная функция гамма -распределения с параметром формы n и параметром масштаба 1. ^{[8] : 176-178  [45]} Этот интервал является « точным » в том смысле, что его вероятность покрытия никогда не бывает меньше номинала 1 – α .${\displaystyle \chi ^{2}(p;n)}$${\displaystyle F^{-1}(p;n,1)}$

Когда квантили гамма-распределения недоступны, была предложена точная аппроксимация этого точного интервала (основанная на преобразовании Уилсона-Хилферти ): ^[46]

${\displaystyle k\left(1-{\frac {1}{9k}}-{\frac {z_{\alpha /2}}{3{\sqrt {k}}}}\right)^{3}\leq \mu \leq (k+1)\left(1-{\frac {1}{9(k+1)}}+{\frac {z_{\alpha /2}}{3{\sqrt {k+1}}}}\right)^{3},}$

где обозначает стандартное нормальное отклонение с верхней зоной хвоста α / 2 .${\displaystyle z_{\alpha /2}}$

Для применения этих формул в том же контексте, что и выше (при наличии выборки из n измеренных значений k _{i ,} каждое из которых взято из распределения Пуассона со средним λ ), можно установить

${\displaystyle k=\sum _{i=1}^{n}k_{i},}$

calculate an interval for μ = n λ , and then derive the interval for λ.

In Bayesian inference, the conjugate prior for the rate parameter λ of the Poisson distribution is the gamma distribution.^[47] Let

${\displaystyle \lambda \sim \mathrm {Gamma} (\alpha ,\beta )}$

denote that λ is distributed according to the gamma density g parameterized in terms of a shape parameter α and an inverse scale parameter β:

${\displaystyle g(\lambda \mid \alpha ,\beta )={\frac {\beta ^{\alpha }}{\Gamma (\alpha )}}\;\lambda ^{\alpha -1}\;e^{-\beta \,\lambda }\qquad {\text{ for }}\lambda >0\,\!.}$

Then, given the same sample of n measured values k_i as before, and a prior of Gamma(α, β), the posterior distribution is

${\displaystyle \lambda \sim \mathrm {Gamma} \left(\alpha +\sum _{i=1}^{n}k_{i},\beta +n\right).}$

Note that the posterior mean is linear and is given by

${\displaystyle E[\lambda \mid k_{1},\ldots ,k_{n}]={\frac {\alpha +\sum _{i=1}^{n}k_{i}}{\beta +n}}.}$

It can be shown that gamma distribution is the only prior that induces linearity of the conditional mean. Moreover, a converse result exists which states that if the conditional mean is close to a linear function in the ${\displaystyle L_{2}}$ distance than the prior distribution of λ must be close to gamma distribution in Levy distance.^[48]

The posterior mean E[λ] approaches the maximum likelihood estimate ${\displaystyle {\widehat {\lambda }}_{\mathrm {MLE} }}$ in the limit as ${\displaystyle \alpha \to 0,\beta \to 0,}$ which follows immediately from the general expression of the mean of the gamma distribution.

The posterior predictive distribution for a single additional observation is a negative binomial distribution,^[49]: 53 sometimes called a gamma–Poisson distribution.

Suppose ${\displaystyle X_{1},X_{2},\dots ,X_{p}}$ is a set of independent random variables from a set of ${\displaystyle p}$ Poisson distributions, each with a parameter ${\displaystyle \lambda _{i},}$ ${\displaystyle i=1,\dots ,p,}$ and we would like to estimate these parameters. Then, Clevenson and Zidek show that under the normalized squared error loss ${\textstyle L(\lambda ,{\hat {\lambda }})=\sum _{i=1}^{p}\lambda _{i}^{-1}({\hat {\lambda }}_{i}-\lambda _{i})^{2},}$ when ${\displaystyle p>1,}$ then, similar as in Stein's example for the Normal means, the MLE estimator ${\displaystyle {\hat {\lambda }}_{i}=X_{i}}$ is inadmissible. ^[50]

In this case, a family of minimax estimators is given for any ${\displaystyle 0<c\leq 2(p-1)}$ and ${\displaystyle b\geq (p-2+p^{-1})}$ as^[51]

${\displaystyle {\hat {\lambda }}_{i}=\left(1-{\frac {c}{b+\sum _{i=1}^{p}X_{i}}}\right)X_{i},\qquad i=1,\dots ,p.}$

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed. Find sources: "Poisson distribution" – news · newspapers · books · scholar · JSTOR (December 2019) (Learn how and when to remove this message)

Some applications of the Poisson distribution to count data (number of events):^[52]

• telecommunication: telephone calls arriving in a system,
• astronomy: photons arriving at a telescope,
• chemistry: the molar mass distribution of a living polymerization,^[53]
• biology: the number of mutations on a strand of DNA per unit length,
• management: customers arriving at a counter or call centre,
• finance and insurance: number of losses or claims occurring in a given period of time,
• seismology: asymptotic Poisson model of risk for large earthquakes,^[54]
• radioactivity: decays in a given time interval in a radioactive sample,
• optics: number of photons emitted in a single laser pulse (a major vulnerability of quantum key distribution protocols, known as photon number splitting).

More examples of counting events that may be modelled as Poisson processes include:

• soldiers killed by horse-kicks each year in each corps in the Prussian cavalry. This example was used in a book by Ladislaus Bortkiewicz (1868–1931),^{[12]: 23-25}
• yeast cells used when brewing Guinness beer. This example was used by William Sealy Gosset (1876–1937),^[55][56]
• phone calls arriving at a call centre within a minute. This example was described by A.K. Erlang (1878–1929),^[57]
• goals in sports involving two competing teams,^[58]
• deaths per year in a given age group,
• jumps in a stock price in a given time interval,
• times a web server is accessed per minute (under an assumption of homogeneity),
• mutations in a given stretch of DNA after a certain amount of radiation,
• cells infected at a given multiplicity of infection,
• bacteria in a certain amount of liquid,^[59]
• photons arriving on a pixel circuit at a given illumination over a given time period,
• landing of V-1 flying bombs on London during World War II, investigated by R. D. Clarke in 1946.^[60]

In probabilistic number theory, Gallagher showed in 1976 that, if a certain version of the unproved prime r-tuple conjecture holds,^[61] then the counts of prime numbers in short intervals would obey a Poisson distribution.^[62]

The rate of an event is related to the probability of an event occurring in some small subinterval (of time, space or otherwise). In the case of the Poisson distribution, one assumes that there exists a small enough subinterval for which the probability of an event occurring twice is "negligible". With this assumption one can derive the Poisson distribution from the binomial one, given only the information of expected number of total events in the whole interval.

Let the total number of events in the whole interval be denoted by ${\displaystyle \lambda .}$ Divide the whole interval into ${\displaystyle n}$ subintervals ${\displaystyle I_{1},\dots ,I_{n}}$ of equal size, such that ${\displaystyle n>\lambda }$ (since we are interested in only very small portions of the interval this assumption is meaningful). This means that the expected number of events in each of the n subintervals is equal to ${\displaystyle \lambda /n.}$

Now we assume that the occurrence of an event in the whole interval can be seen as a sequence of n Bernoulli trials, where the ${\displaystyle i}$-th Bernoulli trial corresponds to looking whether an event happens at the subinterval ${\displaystyle I_{i}}$ with probability ${\displaystyle \lambda /n.}$ The expected number of total events in ${\displaystyle n}$ such trials would be ${\displaystyle \lambda ,}$ the expected number of total events in the whole interval. Hence for each subdivision of the interval we have approximated the occurrence of the event as a Bernoulli process of the form ${\displaystyle {\textrm {B}}(n,\lambda /n).}$ As we have noted before we want to consider only very small subintervals. Therefore, we take the limit as ${\displaystyle n}$ goes to infinity.

In this case the binomial distribution converges to what is known as the Poisson distribution by the Poisson limit theorem.

In several of the above examples — such as, the number of mutations in a given sequence of DNA—the events being counted are actually the outcomes of discrete trials, and would more precisely be modelled using the binomial distribution, that is$${\displaystyle X\sim {\textrm {B}}(n,p).}$$

In such cases n is very large and p is very small (and so the expectation n p is of intermediate magnitude). Then the distribution may be approximated by the less cumbersome Poisson distribution $${\displaystyle X\sim {\textrm {Pois}}(np).}$$

This approximation is sometimes known as the law of rare events,^[63]: 5 since each of the n individual Bernoulli events rarely occurs.

The name "law of rare events" may be misleading because the total count of success events in a Poisson process need not be rare if the parameter n p is not small. For example, the number of telephone calls to a busy switchboard in one hour follows a Poisson distribution with the events appearing frequent to the operator, but they are rare from the point of view of the average member of the population who is very unlikely to make a call to that switchboard in that hour.

The variance of the binomial distribution is 1 − p times that of the Poisson distribution, so almost equal when p is very small.

The word law is sometimes used as a synonym of probability distribution, and convergence in law means convergence in distribution. Accordingly, the Poisson distribution is sometimes called the "law of small numbers" because it is the probability distribution of the number of occurrences of an event that happens rarely but has very many opportunities to happen. The Law of Small Numbers is a book by Ladislaus Bortkiewicz about the Poisson distribution, published in 1898.^[12][64]

The Poisson distribution arises as the number of points of a Poisson point process located in some finite region. More specifically, if D is some region space, for example Euclidean space R^d, for which |D|, the area, volume or, more generally, the Lebesgue measure of the region is finite, and if N(D) denotes the number of points in D, then

${\displaystyle P(N(D)=k)={\frac {(\lambda |D|)^{k}e^{-\lambda |D|}}{k!}}.}$

Poisson regression and negative binomial regression are useful for analyses where the dependent (response) variable is the count (0, 1, 2, ... ) of the number of events or occurrences in an interval.

The Luria–Delbrück experiment tested against the hypothesis of Lamarckian evolution, which should result in a Poisson distribution.

Katz and Miledi measured the membrane potential with and without the presence of acetylcholine (ACh).^[65] When ACh is present, ion channels on the membrane would be open randomly at a small fraction of the time. As there are a large number of ion channels each open for a small fraction of the time, the total number of ion channels open at any moment is Poisson distributed. When ACh is not present, effectively no ion channels are open. The membrane potential is ${\displaystyle V=N_{\text{open}}V_{\text{ion}}+V_{0}+V_{\text{noise}}}$. Subtracting the effect of noise, Katz and Miledi found the mean and variance of membrane potential to be ${\displaystyle 8.5\times 10^{-3}\;\mathrm {V} ,(29.2\times 10^{-6}\;\mathrm {V} )^{2}}$, giving ${\displaystyle V_{\text{ion}}=10^{-7}\;\mathrm {V} }$. (pp. 94-95 ^[66])

During each cellular replication event, the number of mutations is roughly Poisson distributed.^[67] For example, the HIV virus has 10,000 base pairs, and has a mutation rate of about 1 per 30,000 base pairs, meaning the number of mutations per replication event is distributed as ${\displaystyle \mathrm {Pois} (1/3)}$. (p. 64 ^[66])

In a Poisson process, the number of observed occurrences fluctuates about its mean λ with a standard deviation ${\displaystyle \sigma _{k}={\sqrt {\lambda }}.}$ These fluctuations are denoted as Poisson noise or (particularly in electronics) as shot noise.

The correlation of the mean and standard deviation in counting independent discrete occurrences is useful scientifically. By monitoring how the fluctuations vary with the mean signal, one can estimate the contribution of a single occurrence, even if that contribution is too small to be detected directly. For example, the charge e on an electron can be estimated by correlating the magnitude of an electric current with its shot noise. If N electrons pass a point in a given time t on the average, the mean current is ${\displaystyle I=eN/t}$; since the current fluctuations should be of the order ${\displaystyle \sigma _{I}=e{\sqrt {N}}/t}$ (i.e., the standard deviation of the Poisson process), the charge ${\displaystyle e}$ can be estimated from the ratio ${\displaystyle t\sigma _{I}^{2}/I.}$^{[citation needed]}

An everyday example is the graininess that appears as photographs are enlarged; the graininess is due to Poisson fluctuations in the number of reduced silver grains, not to the individual grains themselves. By correlating the graininess with the degree of enlargement, one can estimate the contribution of an individual grain (which is otherwise too small to be seen unaided).^{[citation needed]}

In causal set theory the discrete elements of spacetime follow a Poisson distribution in the volume.

The Poisson distribution also appears in quantum mechanics, especially quantum optics. Namely, for a quantum harmonic oscillator system in a coherent state, the probability of measuring a particular energy level has a Poisson distribution.

The Poisson distribution poses two different tasks for dedicated software libraries: evaluating the distribution ${\displaystyle P(k;\lambda )}$, and drawing random numbers according to that distribution.

Computing ${\displaystyle P(k;\lambda )}$ for given ${\displaystyle k}$ and ${\displaystyle \lambda }$ is a trivial task that can be accomplished by using the standard definition of ${\displaystyle P(k;\lambda )}$ in terms of exponential, power, and factorial functions. However, the conventional definition of the Poisson distribution contains two terms that can easily overflow on computers: λ^k and k!. The fraction of λ^k to k! can also produce a rounding error that is very large compared to e^−λ, and therefore give an erroneous result. For numerical stability the Poisson probability mass function should therefore be evaluated as

${\displaystyle \!f(k;\lambda )=\exp \left[k\ln \lambda -\lambda -\ln \Gamma (k+1)\right],}$

which is mathematically equivalent but numerically stable. The natural logarithm of the Gamma function can be obtained using the lgamma function in the C standard library (C99 version) or R, the gammaln function in MATLAB or SciPy, or the log_gamma function in Fortran 2008 and later.

Some computing languages provide built-in functions to evaluate the Poisson distribution, namely

• R: function dpois(x, lambda);
• Excel: function POISSON( x, mean, cumulative), with a flag to specify the cumulative distribution;
• Mathematica: univariate Poisson distribution as PoissonDistribution[${\displaystyle \lambda }$],^[68] bivariate Poisson distribution as MultivariatePoissonDistribution[${\displaystyle \theta _{12},}${ ${\displaystyle \theta _{1}-\theta _{12},}$ ${\displaystyle \theta _{2}-\theta _{12}}$}],.^[69]