Биномиальное распределение

Биномиальное распределение

Функция массы вероятности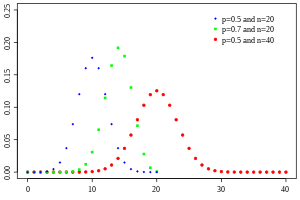
Кумулятивная функция распределения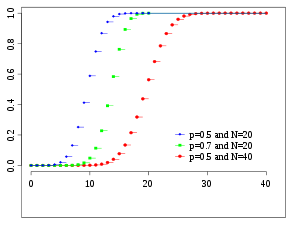
Обозначение	${\displaystyle B(n,p)}$
Параметры	${\displaystyle n\in \{0,1,2,\ldots \}}$– количество попыток – вероятность успеха для каждой попытки ${\displaystyle p\in [0,1]}$ ${\displaystyle q=1-p}$
Поддерживать	${\displaystyle k\in \{0,1,\ldots ,n\}}$– количество успехов
ПМФ	${\displaystyle {\binom {n}{k}}p^{k}q^{nk}}$
СДФ	${\displaystyle I_{q}(n-\lfloor k\rfloor ,1+\lfloor k\rfloor )}$( регуляризованная неполная бета-функция )
Иметь в виду	${\displaystyle np}$
Медиана	${\displaystyle \lfloor np\rfloor}$или${\displaystyle \lceil np\rceil}$
Режим	${\displaystyle \lfloor (n+1)p\rfloor }$или${\displaystyle \lceil (n+1)p\rceil -1}$
Дисперсия	${\displaystyle npq=np(1-p)}$
Асимметрия	${\displaystyle {\frac {qp}{\sqrt {npq}}}}$
Избыточный эксцесс	${\displaystyle {\frac {1-6pq}{npq}}}$
Энтропия	${\displaystyle {\frac {1}{2}}\log _{2}(2\pi enpq)+O\left({\frac {1}{n}}\right)}$ в шеннонах . Для нат используйте натуральный логарифм в логарифме.
МГФ	${\displaystyle (q+pe^{t})^{n}}$
CF	${\displaystyle (q+pe^{it})^{n}}$
ПГФ	${\displaystyle G(z)=[q+pz]^{n}}$
Информация о Фишере	${\displaystyle g_{n}(p)={\frac {n}{pq}}}$ (для фиксированного )${\displaystyle n}$

Часть серии по статистике
Теория вероятностей
Вероятность Аксиомы Детерминизм Система Индетерминизм Случайность
Вероятностное пространство Образец пространства Событие В совокупности исчерпывающие события Элементарное событие Взаимная исключительность Исход Синглтон Эксперимент процесс Бернулли Распределение вероятностей Распределение Бернулли Биномиальное распределение Экспоненциальное распределение Нормальное распределение Распределение Парето Распределение Пуассона Мера вероятности Случайная величина процесс Бернулли Непрерывный или дискретный Ожидаемое значение Дисперсия цепь Маркова Наблюдаемое значение Случайное блуждание Случайный процесс
Дополнительное мероприятие Совместная вероятность Предельная вероятность Условная вероятность
Независимость Условная независимость Закон полной вероятности Закон больших чисел Теорема Байеса Неравенство Буля
Диаграмма Венна Древовидная диаграмма
в т е

В теории вероятностей и статистике биномиальное распределение с параметрами n и p — это дискретное распределение вероятностей числа успехов в последовательности из n независимых экспериментов , каждый из которых задает вопрос типа «да-нет» , и каждый имеет свой собственный булевский результат : успех (с вероятностью p ) или неудача (с вероятностью q = 1- p ). Одиночный эксперимент с успехом/неудачей также называется испытанием Бернулли или экспериментом Бернулли, а последовательность результатов называется процессом Бернулли ; для одного испытания, т. е. n = 1 , биномиальное распределение является распределением Бернулли . Биномиальное распределение является основой для популярного биномиального теста статистической значимости . ^[1]

Биномиальное распределение часто используется для моделирования числа успехов в выборке размера n, взятой с заменой из популяции размера N. Если выборка осуществляется без замены, выборки не являются независимыми, и поэтому результирующее распределение является гипергеометрическим распределением , а не биномиальным. Однако для N , намного больших, чем n , биномиальное распределение остается хорошим приближением и широко используется.

В общем случае, если случайная величина X следует биномиальному распределению с параметрами n ∈${\displaystyle \mathbb {N} }$ и p ∈ [0, 1] , мы записываем X ~ B ( n , p ) . Вероятность получения ровно k успехов в n независимых испытаниях Бернулли (с той же частотой p ) задается функцией массы вероятности :

${\displaystyle f(k,n,p)=\Pr(X=k)={\binom {n}{k}}p^{k}(1-p)^{n-k}}$

для k = 0, 1, 2, ..., n , где

${\displaystyle {\binom {n}{k}}={\frac {n!}{k!(n-k)!}}}$

- биномиальный коэффициент , отсюда и название распределения. Формулу можно понять следующим образом: p ^k q ^{n - k} - вероятность получения последовательности из n независимых испытаний Бернулли, в которой k испытаний являются «успехами», а оставшиеся n - k испытаний приводят к «неуспеху». Поскольку испытания независимы, а вероятности между ними остаются постоянными, любая последовательность из n испытаний с k успехами (и n - k неудачами) имеет одинаковую вероятность быть достигнутой (независимо от позиций успехов в последовательности). Такие последовательности существуют, поскольку биномиальный коэффициент подсчитывает количество способов выбора позиций k успехов среди n испытаний. Биномиальное распределение касается вероятности получения любой из этих последовательностей, то есть вероятность получения одной из них ( p ^k q ^{n - k} ) должна быть сложена раз, следовательно .${\textstyle {\binom {n}{k}}}$${\textstyle {\binom {n}{k}}}$ ${\textstyle {\binom {n}{k}}}$${\textstyle \Pr(X=k)={\binom {n}{k}}p^{k}(1-p)^{n-k}}$

При создании справочных таблиц для вероятности биномиального распределения, как правило, таблица заполняется до n / 2 значений. Это связано с тем, что при k > n / 2 вероятность может быть рассчитана по ее дополнению как

${\displaystyle f(k,n,p)=f(n-k,n,1-p).}$

Рассматривая выражение f ( k , n , p ) как функцию k , существует значение k , которое максимизирует его. Это значение k можно найти, вычислив

${\displaystyle {\frac {f(k+1,n,p)}{f(k,n,p)}}={\frac {(n-k)p}{(k+1)(1-p)}}}$

и сравнивая его с 1. Всегда существует целое число M , которое удовлетворяет ^[2]

${\displaystyle (n+1)p-1\leq M<(n+1)p.}$

f ( k , n , p ) монотонно возрастает при k < M и монотонно убывает при k > M , за исключением случая, когда ( n  + 1) p является целым числом. В этом случае есть два значения, для которых f максимальна: ( n + 1) p и ( n + 1) p - 1 . M является наиболее вероятным результатом (то есть наиболее вероятным, хотя это все еще может быть маловероятным в целом) испытаний Бернулли и называется модой .

Эквивалентно, . Взяв функцию пола , мы получаем M = пол( np ) . ^{[примечание 1]}${\displaystyle M-p<np\leq M+1-p}$

Предположим, что при подбрасывании несимметричной монеты выпадает орел с вероятностью 0,3. Вероятность увидеть ровно 4 орла при 6 подбрасываниях равна

${\displaystyle f(4,6,0.3)={\binom {6}{4}}0.3^{4}(1-0.3)^{6-4}=0.059535.}$

Кумулятивную функцию распределения можно выразить как:

${\displaystyle F(k;n,p)=\Pr(X\leq k)=\sum _{i=0}^{\lfloor k\rfloor }{n \choose i}p^{i}(1-p)^{n-i},}$

где — «пол» под k , т.е. наибольшее целое число, меньшее или равное k .${\displaystyle \lfloor k\rfloor }$

Его также можно представить в терминах регуляризованной неполной бета-функции следующим образом: ^[3]

${\displaystyle {\begin{aligned}F(k;n,p)&=\Pr(X\leq k)\\&=I_{1-p}(n-k,k+1)\\&=(n-k){n \choose k}\int _{0}^{1-p}t^{n-k-1}(1-t)^{k}\,dt.\end{aligned}}}$

что эквивалентно кумулятивной функции распределения F -распределения : [ ^4]

${\displaystyle F(k;n,p)=F_{F{\text{-distribution}}}\left(x={\frac {1-p}{p}}{\frac {k+1}{n-k}};d_{1}=2(n-k),d_{2}=2(k+1)\right).}$

Ниже приведены некоторые замкнутые границы для кумулятивной функции распределения.

Если X ~ B ( n , p ) , то есть X — биномиально распределенная случайная величина, где n — общее число экспериментов, а p — вероятность того, что каждый эксперимент даст успешный результат, то ожидаемое значение X равно: ^[5 ]

${\displaystyle \operatorname {E} [X]=np.}$

Это следует из линейности ожидаемого значения, а также из того факта, что X представляет собой сумму n идентичных случайных величин Бернулли, каждая из которых имеет ожидаемое значение p . Другими словами, если являются идентичными (и независимыми) случайными величинами Бернулли с параметром p , то и${\displaystyle X_{1},\ldots ,X_{n}}$${\displaystyle X=X_{1}+\cdots +X_{n}}$

${\displaystyle \operatorname {E} [X]=\operatorname {E} [X_{1}+\cdots +X_{n}]=\operatorname {E} [X_{1}]+\cdots +\operatorname {E} [X_{n}]=p+\cdots +p=np.}$

Дисперсия составляет :

${\displaystyle \operatorname {Var} (X)=npq=np(1-p).}$

Это аналогичным образом следует из того факта, что дисперсия суммы независимых случайных величин равна сумме дисперсий.

Первые 6 центральных моментов , определяемые как , задаются формулой ${\displaystyle \mu _{c}=\operatorname {E} \left[(X-\operatorname {E} [X])^{c}\right]}$

${\displaystyle {\begin{aligned}\mu _{1}&=0,\\\mu _{2}&=np(1-p),\\\mu _{3}&=np(1-p)(1-2p),\\\mu _{4}&=np(1-p)(1+(3n-6)p(1-p)),\\\mu _{5}&=np(1-p)(1-2p)(1+(10n-12)p(1-p)),\\\mu _{6}&=np(1-p)(1-30p(1-p)(1-4p(1-p))+5np(1-p)(5-26p(1-p))+15n^{2}p^{2}(1-p)^{2}).\end{aligned}}}$

Нецентральные моменты удовлетворяют

${\displaystyle {\begin{aligned}\operatorname {E} [X]&=np,\\\operatorname {E} [X^{2}]&=np(1-p)+n^{2}p^{2},\end{aligned}}}$

и вообще ^{[6] [7]}

${\displaystyle \operatorname {E} [X^{c}]=\sum _{k=0}^{c}\left\{{c \atop k}\right\}n^{\underline {k}}p^{k},}$

где — числа Стирлинга второго рода , а — y- я падающая степень . Простая граница ^[8] следует из ограничения биномиальных моментов через высшие моменты Пуассона : ${\displaystyle \textstyle \left\{{c \atop k}\right\}}$${\displaystyle n^{\underline {k}}=n(n-1)\cdots (n-k+1)}$${\displaystyle k}$${\displaystyle n}$

${\displaystyle \operatorname {E} [X^{c}]\leq \left({\frac {c}{\log(c/(np)+1)}}\right)^{c}\leq (np)^{c}\exp \left({\frac {c^{2}}{2np}}\right).}$

Это показывает, что если , то отстоит от${\displaystyle c=O({\sqrt {np}})}$${\displaystyle \operatorname {E} [X^{c}]}$${\displaystyle \operatorname {E} [X]^{c}}$

Обычно мода биномиального распределения B ( n ,  p ) равна , где — функция пола . Однако, когда ( n  + 1) p — целое число, а p не равно ни 0, ни 1, то распределение имеет две моды: ( n  + 1) p и ( n  + 1) p  − 1. Когда p равно 0 или 1, мода будет равна 0 и n соответственно. Эти случаи можно обобщить следующим образом:${\displaystyle \lfloor (n+1)p\rfloor }$${\displaystyle \lfloor \cdot \rfloor }$

${\displaystyle {\text{mode}}={\begin{cases}\lfloor (n+1)\,p\rfloor &{\text{if }}(n+1)p{\text{ is 0 or a noninteger}},\\(n+1)\,p\ {\text{ and }}\ (n+1)\,p-1&{\text{if }}(n+1)p\in \{1,\dots ,n\},\\n&{\text{if }}(n+1)p=n+1.\end{cases}}}$

Доказательство: Пусть

${\displaystyle f(k)={\binom {n}{k}}p^{k}q^{n-k}.}$

Для имеет ненулевое значение только при . Для мы находим и для . Это доказывает, что мода равна 0 для и для .${\displaystyle p=0}$${\displaystyle f(0)}$${\displaystyle f(0)=1}$${\displaystyle p=1}$${\displaystyle f(n)=1}$${\displaystyle f(k)=0}$${\displaystyle k\neq n}$${\displaystyle p=0}$${\displaystyle n}$${\displaystyle p=1}$

Пусть . Находим${\displaystyle 0<p<1}$

${\displaystyle {\frac {f(k+1)}{f(k)}}={\frac {(n-k)p}{(k+1)(1-p)}}}$.

Из этого следует

${\displaystyle {\begin{aligned}k>(n+1)p-1\Rightarrow f(k+1)<f(k)\\k=(n+1)p-1\Rightarrow f(k+1)=f(k)\\k<(n+1)p-1\Rightarrow f(k+1)>f(k)\end{aligned}}}$

Так что когда — целое число, то и — мода. В случае, когда , то только — мода. ^[9]${\displaystyle (n+1)p-1}$${\displaystyle (n+1)p-1}$${\displaystyle (n+1)p}$${\displaystyle (n+1)p-1\notin \mathbb {Z} }$${\displaystyle \lfloor (n+1)p-1\rfloor +1=\lfloor (n+1)p\rfloor }$

В общем случае не существует единой формулы для нахождения медианы для биномиального распределения, и она может быть даже не уникальной. Однако было установлено несколько специальных результатов:

• Если — целое число, то среднее значение, медиана и мода совпадают и равны . ^{[10] [11]}${\displaystyle np}$${\displaystyle np}$
• Любая медиана m должна лежать в пределах интервала . ^[12]${\displaystyle \lfloor np\rfloor \leq m\leq \lceil np\rceil }$
• Медиана m не может лежать слишком далеко от среднего значения: . ^[13]${\displaystyle |m-np|\leq \min\{{\ln 2},\max\{p,1-p\}\}}$
• Медиана уникальна и равна m  =  round ( np ), когда (за исключением случая, когда и n нечетно). ^[12]${\displaystyle |m-np|\leq \min\{p,1-p\}}$${\displaystyle p={\frac {1}{2}}}$
• Когда p — рациональное число (за исключением и нечетных n ), медиана уникальна. ^[14]${\displaystyle p={\frac {1}{2}}}$
• Когда и n нечетно, любое число m в интервале является медианой биномиального распределения. Если и n четно, то является уникальной медианой.${\displaystyle p={\frac {1}{2}}}$${\displaystyle {\frac {1}{2}}{\bigl (}n-1{\bigr )}\leq m\leq {\frac {1}{2}}{\bigl (}n+1{\bigr )}}$${\displaystyle p={\frac {1}{2}}}$${\displaystyle m={\frac {n}{2}}}$

Для k ≤ np можно вывести верхние границы для нижнего хвоста кумулятивной функции распределения , вероятности того, что будет не более k успехов. Поскольку , эти границы можно также рассматривать как границы для верхнего хвоста кумулятивной функции распределения для k ≥ np .${\displaystyle F(k;n,p)=\Pr(X\leq k)}$${\displaystyle \Pr(X\geq k)=F(n-k;n,1-p)}$

Неравенство Хеффдинга дает простую оценку

${\displaystyle F(k;n,p)\leq \exp \left(-2n\left(p-{\frac {k}{n}}\right)^{2}\right),\!}$

что, однако, не очень точно. В частности, для p = 1 мы имеем, что F ( k ; n , p ) = 0 (для фиксированных k , n с k  <  n ), но граница Хеффдинга оценивается как положительная константа.

Более точную границу можно получить из границы Чернова : ^[15]

${\displaystyle F(k;n,p)\leq \exp \left(-nD\left({\frac {k}{n}}\parallel p\right)\right)}$

где D ( a || p ) — относительная энтропия (или расхождение Кульбака-Лейблера) между a -монетой и p -монетой (т.е. между распределениями Бернулли( a ) и Бернулли( p ):

${\displaystyle D(a\parallel p)=(a)\log {\frac {a}{p}}+(1-a)\log {\frac {1-a}{1-p}}.\!}$

Асимптотически эта граница достаточно точна; подробности см. в ^{[15] .}

Можно также получить нижние границы хвоста , известные как антиконцентрационные границы. Аппроксимируя биномиальный коэффициент формулой Стирлинга, можно показать, что ^[16]${\displaystyle F(k;n,p)}$

${\displaystyle F(k;n,p)\geq {\frac {1}{\sqrt {8n{\tfrac {k}{n}}(1-{\tfrac {k}{n}})}}}\exp \left(-nD\left({\frac {k}{n}}\parallel p\right)\right),}$

что подразумевает более простую, но менее жесткую связь

${\displaystyle F(k;n,p)\geq {\frac {1}{\sqrt {2n}}}\exp \left(-nD\left({\frac {k}{n}}\parallel p\right)\right).}$

При p = 1/2 и k ≥ 3 n /8 для четных n можно сделать знаменатель постоянным: ^[17]

${\displaystyle F(k;n,{\tfrac {1}{2}})\geq {\frac {1}{15}}\exp \left(-16n\left({\frac {1}{2}}-{\frac {k}{n}}\right)^{2}\right).\!}$

Если n известно, параметр p можно оценить, используя долю успехов:

${\displaystyle {\widehat {p}}={\frac {x}{n}}.}$

Эта оценка найдена с использованием оценки максимального правдоподобия , а также метода моментов . Эта оценка является несмещенной и равномерной с минимальной дисперсией , что доказано с помощью теоремы Лемана–Шеффе , поскольку она основана на минимальной достаточной и полной статистике (т.е.: x ). Она также последовательна как по вероятности, так и по среднеквадратической ошибке .

Замкнутая форма байесовской оценки для p также существует при использовании бета-распределения в качестве сопряженного априорного распределения . При использовании общего априорного распределения апостериорная средняя оценка имеет вид:${\displaystyle \operatorname {Beta} (\alpha ,\beta )}$

${\displaystyle {\widehat {p}}_{b}={\frac {x+\alpha }{n+\alpha +\beta }}.}$

Оценка Байеса асимптотически эффективна , и по мере того, как размер выборки стремится к бесконечности ( n → ∞), она приближается к решению MLE . ^[18] Оценка Байеса смещена (степень смещения зависит от априорных данных), допустима и последовательна по вероятности.

Для частного случая использования стандартного равномерного распределения в качестве неинформативного априорного распределения , апостериорная средняя оценка становится:${\displaystyle \operatorname {Beta} (\alpha =1,\beta =1)=U(0,1)}$

${\displaystyle {\widehat {p}}_{b}={\frac {x+1}{n+2}}.}$

( Апостериорный метод должен просто привести к стандартной оценке.) Этот метод называется правилом последовательности и был введен в XVIII веке Пьером-Симоном Лапласом .

При использовании априорной вероятности Джеффри априорная вероятность равна , ^[19] что приводит к оценке:${\displaystyle \operatorname {Beta} (\alpha ={\frac {1}{2}},\beta ={\frac {1}{2}})}$

${\displaystyle {\widehat {p}}_{Jeffreys}={\frac {x+{\frac {1}{2}}}{n+1}}.}$

При оценке p с очень редкими событиями и малым n (например: если x=0), то использование стандартной оценки приводит к тому, что иногда нереалистично и нежелательно. В таких случаях существуют различные альтернативные оценки. ^[20] Один из способов — использовать оценку Байеса , что приводит к:${\displaystyle {\widehat {p}}=0,}$${\displaystyle {\widehat {p}}_{b}}$

${\displaystyle {\widehat {p}}_{b}={\frac {1}{n+2}}.}$

Другой метод — использовать верхнюю границу доверительного интервала , полученную с помощью правила трех :

${\displaystyle {\widehat {p}}_{\text{rule of 3}}={\frac {3}{n}}.}$

Даже для довольно больших значений n фактическое распределение среднего значения существенно ненормально. ^[21] Из-за этой проблемы было предложено несколько методов оценки доверительных интервалов.

В приведенных ниже уравнениях для доверительных интервалов переменные имеют следующее значение:

• n ₁ — количество успехов из n , общего количества попыток
• ${\displaystyle {\widehat {p\,}}={\frac {n_{1}}{n}}}$это доля успехов
• ${\displaystyle z}$это квантиль стандартного нормального распределения (т.е. пробит ), соответствующий целевой частоте ошибок . Например, для уровня достоверности 95% ошибка  = 0,05, поэтому  = 0,975 и  = 1,96.${\displaystyle 1-{\tfrac {1}{2}}\alpha }$ ${\displaystyle \alpha }$${\displaystyle \alpha }$${\displaystyle 1-{\tfrac {1}{2}}\alpha }$${\displaystyle z}$

${\displaystyle {\widehat {p\,}}\pm z{\sqrt {\frac {{\widehat {p\,}}(1-{\widehat {p\,}})}{n}}}.}$

Может быть добавлена ​​поправка на непрерывность 0,5/ n . ^{[ необходимо разъяснение ]}

^[22]

${\displaystyle {\tilde {p}}\pm z{\sqrt {\frac {{\tilde {p}}(1-{\tilde {p}})}{n+z^{2}}}}}$

Здесь оценка p изменяется на

${\displaystyle {\tilde {p}}={\frac {n_{1}+{\frac {1}{2}}z^{2}}{n+z^{2}}}}$

Этот метод хорошо работает для и . ^[23] См. здесь для . ^[24] Для используйте метод Уилсона (оценка) ниже.${\displaystyle n>10}$${\displaystyle n_{1}\neq 0,n}$${\displaystyle n\leq 10}$${\displaystyle n_{1}=0,n}$

^[25]

${\displaystyle \sin ^{2}\left(\arcsin \left({\sqrt {\widehat {p\,}}}\right)\pm {\frac {z}{2{\sqrt {n}}}}\right).}$

Обозначения в приведенной ниже формуле отличаются от предыдущих формул в двух отношениях: ^[26]

• Во-первых, z _x имеет несколько иную интерпретацию в приведенной ниже формуле: она имеет обычное значение « x- й квантиль стандартного нормального распределения», а не является сокращением для «(1 −  x )-й квантиль».
• Во-вторых, эта формула не использует знак плюс-минус для определения двух границ. Вместо этого можно использовать для получения нижней границы или использовать для получения верхней границы. Например: для уровня достоверности 95% ошибка  = 0,05, поэтому нижнюю границу можно получить, используя , а верхнюю — используя .${\displaystyle z=z_{\alpha /2}}$${\displaystyle z=z_{1-\alpha /2}}$${\displaystyle \alpha }$${\displaystyle z=z_{\alpha /2}=z_{0.025}=-1.96}$${\displaystyle z=z_{1-\alpha /2}=z_{0.975}=1.96}$

${\displaystyle {\frac {{\widehat {p\,}}+{\frac {z^{2}}{2n}}+z{\sqrt {{\frac {{\widehat {p\,}}(1-{\widehat {p\,}})}{n}}+{\frac {z^{2}}{4n^{2}}}}}}{1+{\frac {z^{2}}{n}}}}}$^[27]

Так называемый «точный» ( метод Клоппера–Пирсона ) является наиболее консервативным. ^[21] ( Точный не означает абсолютно точный; скорее, это означает, что оценки не будут менее консервативными, чем истинное значение.)

Метод Вальда, хотя и часто рекомендуемый в учебниках, является наиболее предвзятым. ^{[ необходимо разъяснение ]}

Если X  ~ B( n ,  p ) и Y  ~ B( m ,  p ) являются независимыми биномиальными переменными с одинаковой вероятностью p , то X  +  Y снова является биномиальной переменной; ее распределение имеет вид Z=X+Y  ~ B( n+m ,  p ): ^[28]

${\displaystyle {\begin{aligned}\operatorname {P} (Z=k)&=\sum _{i=0}^{k}\left[{\binom {n}{i}}p^{i}(1-p)^{n-i}\right]\left[{\binom {m}{k-i}}p^{k-i}(1-p)^{m-k+i}\right]\\&={\binom {n+m}{k}}p^{k}(1-p)^{n+m-k}\end{aligned}}}$

Биномиально распределенную случайную величину X  ~ B( n ,  p ) можно рассматривать как сумму n случайных величин, распределенных по закону Бернулли. Таким образом, сумма двух биномиально распределенных случайных величин X  ~ B( n ,  p ) и Y  ~ B( m ,  p ) эквивалентна сумме n  +  m случайных величин, распределенных по закону Бернулли, что означает Z=X+Y  ~ B( n+m ,  p ). Это также можно доказать напрямую, используя правило сложения.

Однако если X и Y не имеют одинаковой вероятности p , то дисперсия суммы будет меньше дисперсии биномиальной переменной, распределенной как${\displaystyle B(n+m,{\bar {p}}).\,}$

Биномиальное распределение является частным случаем биномиального распределения Пуассона , которое является распределением суммы n независимых неидентичных испытаний Бернулли B( p _i ). ^[29]

Этот результат был впервые получен Кацем и соавторами в 1978 году. ^[30]

Пусть X ~ B( n , p ₁ ) и Y ~ B( m , p ₂ ) независимы. Пусть T = ( X / n ) / ( Y / m ) .

Тогда log( T ) приблизительно нормально распределен со средним log( p ₁ / p ₂ ) и дисперсией ((1/ p ₁ ) − 1)/ n + ((1/ p ₂ ) − 1)/ m .

Если X  ~ B( n ,  p ) и Y  |  X  ~ B( X ,  q ) (условное распределение Y при заданном  X ), то Y является простой биномиальной случайной величиной с распределением Y  ~ B( n ,  pq ).

Например, представьте, что вы бросаете n мячей в корзину U _X и забираете мячи, которые попали, и бросаете их в другую корзину U _Y . Если p — вероятность попадания в U _X , то X  ~ B( n ,  p ) — количество мячей, которые попали в U _X . Если q — вероятность попадания в U _Y, то количество мячей, которые попали в U _{Y ,} равно Y  ~ B( X ,  q ) и, следовательно, Y  ~ B( n ,  pq ).

Распределение Бернулли является частным случаем биномиального распределения, где n  = 1. Символически X  ~ B(1,  p ) имеет то же значение, что и X  ~ Bernoulli( p ). Наоборот, любое биномиальное распределение, B( n ,  p ), является распределением суммы n независимых испытаний Бернулли , Bernoulli( p ), каждое с одинаковой вероятностью p . ^[31]

Если n достаточно велико, то перекос распределения не слишком велик. В этом случае разумное приближение к B( n ,  p ) дается нормальным распределением

${\displaystyle {\mathcal {N}}(np,\,np(1-p)),}$

и это базовое приближение может быть улучшено простым способом с помощью подходящей коррекции непрерывности . Базовое приближение обычно улучшается с ростом n (по крайней мере 20) и лучше, когда p не близко к 0 или 1. ^[32] Различные эмпирические правила могут быть использованы для определения того, достаточно ли велико n , и достаточно ли далеко p от крайних значений нуля или единицы:

• Одно из правил ^[32] заключается в том, что для n > 5 нормальное приближение является адекватным, если абсолютное значение асимметрии строго меньше 0,3; то есть, если

${\displaystyle {\frac {|1-2p|}{\sqrt {np(1-p)}}}={\frac {1}{\sqrt {n}}}\left|{\sqrt {\frac {1-p}{p}}}-{\sqrt {\frac {p}{1-p}}}\,\right|<0.3.}$

Это можно уточнить, используя теорему Берри–Эссеена .

• Более строгое правило гласит, что нормальное приближение применимо только в том случае, если все, что находится в пределах 3 стандартных отклонений от его среднего значения, находится в пределах диапазона возможных значений; то есть только если

${\displaystyle \mu \pm 3\sigma =np\pm 3{\sqrt {np(1-p)}}\in (0,n).}$

Это правило трех стандартных отклонений эквивалентно следующим условиям, которые также подразумевают первое правило выше.

${\displaystyle n>9\left({\frac {1-p}{p}}\right)\quad {\text{and}}\quad n>9\left({\frac {p}{1-p}}\right).}$

• Другое часто используемое правило заключается в том, что оба значения и должны быть больше ^{[33] [34]} или равны 5. Однако конкретное число варьируется от источника к источнику и зависит от того, насколько хорошее приближение требуется. В частности, если использовать 9 вместо 5, правило подразумевает результаты, указанные в предыдущих параграфах.${\displaystyle np}$${\displaystyle n(1-p)}$

Ниже приведен пример применения коррекции непрерывности . Предположим, что требуется вычислить Pr( X  ≤ 8) для биномиальной случайной величины X. Если Y имеет распределение, заданное нормальным приближением, то Pr( X  ≤ 8) аппроксимируется Pr( Y  ≤ 8,5). Добавление 0,5 является коррекцией непрерывности; неисправленное нормальное приближение дает значительно менее точные результаты.

Это приближение, известное как теорема Муавра–Лапласа , значительно экономит время при выполнении вычислений вручную (точные вычисления с большими n очень обременительны); исторически это было первое использование нормального распределения, введенное в книге Абрахама де Муавра «Учение о шансах » в 1738 году. В настоящее время его можно рассматривать как следствие центральной предельной теоремы, поскольку B( n ,  p ) представляет собой сумму n независимых, одинаково распределенных переменных Бернулли с параметром  p . Этот факт является основой проверки гипотезы , «z-теста пропорции», для значения p с использованием x/n , выборочной пропорции и оценки p , в общей тестовой статистике . ^[35]

Например, предположим, что кто-то случайно выбирает n человек из большой популяции и спрашивает их, согласны ли они с определенным утверждением. Доля людей, которые согласны, конечно, будет зависеть от выборки. Если бы группы из n человек были выбраны повторно и действительно случайным образом, пропорции следовали бы приблизительно нормальному распределению со средним значением, равным истинной пропорции согласия в популяции p , и со стандартным отклонением

${\displaystyle \sigma ={\sqrt {\frac {p(1-p)}{n}}}}$

Биномиальное распределение сходится к распределению Пуассона , когда число испытаний стремится к бесконечности, в то время как произведение np сходится к конечному пределу. Следовательно, распределение Пуассона с параметром λ = np может быть использовано в качестве приближения к B( n , p ) биномиального распределения, если n достаточно велико, а p достаточно мало. Согласно эмпирическим правилам, это приближение является хорошим, если n  ≥ 20 и p  ≤ 0,05 ^[36] таким образом, что np ≤ 1, или если n > 50 и p < 0,1 таким образом, что np < 5, ^[37] или если n  ≥ 100 и np  ≤ 10. ^{[38] [39]}

Относительно точности приближения Пуассона см. Новак, ^[40], гл. 4, и приведенные там ссылки.

• Предельная теорема Пуассона : Когда n стремится к ∞, а p стремится к 0 при фиксированномпроизведении np , биномиальное ( n ,  p ) распределение приближается к распределению Пуассона с ожидаемым значением λ = np . ^[38]
• Теорема Муавра–Лапласа : Когда n стремится к ∞, а p остается фиксированным, распределение

${\displaystyle {\frac {X-np}{\sqrt {np(1-p)}}}}$

приближается к нормальному распределению с ожидаемым значением 0 и дисперсией  1. Этот результат иногда грубо формулируют, говоря, что распределение X является асимптотически нормальным с ожидаемым значением 0 и дисперсией  1. Этот результат является частным случаем центральной предельной теоремы .

Биномиальное распределение и бета-распределение — это разные представления одной и той же модели повторных испытаний Бернулли. Биномиальное распределение — это PMF k успехов при n независимых событиях, каждое из которых имеет вероятность успеха p . Математически , когда α = k + 1 и β = n − k + 1 , бета-распределение и биномиальное распределение связаны ^{[ требуется разъяснение ]} множителем n + 1 :

${\displaystyle \operatorname {Beta} (p;\alpha ;\beta )=(n+1)B(k;n;p)}$

Бета-распределения также предоставляют семейство априорных распределений вероятностей для биномиальных распределений в байесовском выводе : ^[41]

${\displaystyle P(p;\alpha ,\beta )={\frac {p^{\alpha -1}(1-p)^{\beta -1}}{\operatorname {Beta} (\alpha ,\beta )}}.}$

При наличии однородного априорного распределения апостериорное распределение вероятности успеха p при n независимых событиях с k наблюдаемыми успехами представляет собой бета-распределение. ^[42]

Методы генерации случайных чисел , где маргинальное распределение является биномиальным распределением, хорошо известны. ^{[43] [44]} Одним из способов генерации случайных выборок из биномиального распределения является использование алгоритма инверсии. Для этого необходимо вычислить вероятность того, что Pr( X = k ) для всех значений k от 0 до n . (Эти вероятности должны суммироваться до значения, близкого к единице, чтобы охватить все пространство выборки.) Затем, используя генератор псевдослучайных чисел для генерации выборок равномерно между 0 и 1, можно преобразовать вычисленные выборки в дискретные числа, используя вероятности, вычисленные на первом этапе.

Это распределение было получено Якобом Бернулли . Он рассмотрел случай, когда p = r /( r  +  s ), где p — вероятность успеха, а r и s — положительные целые числа. Блез Паскаль ранее рассмотрел случай, когда p  = 1/2, составив таблицу соответствующих биномиальных коэффициентов в том, что сейчас известно как треугольник Паскаля . ^[45]

• Логистическая регрессия
• Мультиномиальное распределение
• Отрицательное биномиальное распределение
• Бета-биномиальное распределение
• Биномиальная мера, пример мультифрактальной меры . ^[46]
• Статистическая механика
• Лемма о нагромождении , результирующая вероятность при выполнении операции XOR с независимыми булевыми переменными

• Хирш, Вернер З. (1957). «Биномиальное распределение — успех или неудача, насколько они вероятны?». Введение в современную статистику . Нью-Йорк: MacMillan. С. 140–153.
• Нетер, Джон; Вассерман, Уильям; Уитмор, Джорджия (1988). Прикладная статистика (Третье изд.). Бостон: Аллин и Бэкон. стр. 185–192. ISBN 0-205-10328-6.

На Викискладе есть медиафайлы по теме Биномиальные распределения .

• Интерактивная графика: Одномерные распределительные соотношения
• Калькулятор формулы биномиального распределения
• Разность двух биномиальных величин: XY или |XY|
• Запрос биномиального распределения вероятностей в WolframAlpha
• Доверительные (вероятные) интервалы для биномиальной вероятности, p: онлайн-калькулятор доступен на сайте causaScientia.org