Минимаксная оценка

В статистической теории принятия решений , где мы сталкиваемся с проблемой оценки детерминированного параметра (вектора) из наблюдений, оценщик ( правило оценки) называется минимаксным, если его максимальный риск минимален среди всех оценщиков . В некотором смысле это означает, что — оценщик, который работает лучше всего в наихудшем возможном случае, допустимом в задаче. θ ∈ Θ {\displaystyle \theta \in \Theta } х ∈ Х , {\displaystyle x\in {\mathcal {X}},} δ M {\displaystyle \delta ^{M}\,\!} θ {\displaystyle \theta \,\!} δ M {\displaystyle \delta ^{M}\,\!}

Настройка проблемы

Рассмотрим задачу оценки детерминированного (не байесовского ) параметра из зашумленных или поврежденных данных , связанных через условное распределение вероятностей . Наша цель — найти «хорошую» оценку для оценки параметра , которая минимизирует некоторую заданную функцию риска . Здесь функция риска (технически функциональная или операторная, поскольку является функцией функции, а НЕ композицией функций) — это ожидание некоторой функции потерь относительно . Популярным примером функции потерь [1] является квадратичная ошибка потерь , а функцией риска для этой потери является средняя квадратичная ошибка (MSE). θ ∈ Θ {\displaystyle \theta \in \Theta } x ∈ X {\displaystyle x\in {\mathcal {X}}} P ( x ∣ θ ) {\displaystyle P(x\mid \theta )\,\!} δ ( x ) {\displaystyle \delta (x)\,\!} θ {\displaystyle \theta \,\!} R ( θ , δ ) {\displaystyle R(\theta ,\delta )\,\!} R {\displaystyle R} L ( θ , δ ) {\displaystyle L(\theta ,\delta )\,\!} P ( x ∣ θ ) {\displaystyle P(x\mid \theta )\,\!} L ( θ , δ ) = ‖ θ − δ ‖ 2 {\displaystyle L(\theta ,\delta )=\|\theta -\delta \|^{2}\,\!}

К сожалению, в общем случае риск не может быть минимизирован, поскольку он зависит от самого неизвестного параметра (если бы мы знали, каково фактическое значение , нам не нужно было бы его оценивать). Поэтому требуются дополнительные критерии для нахождения оптимальной в некотором смысле оценки. Одним из таких критериев является критерий минимакса. θ {\displaystyle \theta \,\!} θ {\displaystyle \theta \,\!}

Определение

Определение  : Оценка называется минимаксной по отношению к функции риска , если она достигает наименьшего максимального риска среди всех оценок, то есть она удовлетворяет δ M : X → Θ {\displaystyle \delta ^{M}:{\mathcal {X}}\rightarrow \Theta \,\!} R ( θ , δ ) {\displaystyle R(\theta ,\delta )\,\!}

sup θ ∈ Θ R ( θ , δ M ) = inf δ sup θ ∈ Θ R ( θ , δ ) . {\displaystyle \sup _{\theta \in \Theta }R(\theta ,\delta ^{M})=\inf _{\delta }\sup _{\theta \in \Theta }R(\theta ,\delta ).\,}

Наименее благоприятное распределение

Логически, оценка минимаксна, когда она является лучшей в худшем случае. Продолжая эту логику, оценка минимакса должна быть байесовской оценкой относительно наименее благоприятного априорного распределения . Чтобы продемонстрировать это понятие, обозначим средний риск байесовской оценки относительно априорного распределения как θ {\displaystyle \theta \,\!} δ π {\displaystyle \delta _{\pi }\,\!} π {\displaystyle \pi \,\!}

r π = ∫ R ( θ , δ π ) d π ( θ ) {\displaystyle r_{\pi }=\int R(\theta ,\delta _{\pi })\,d\pi (\theta )\,}

Определение: Априорное распределение называется наименее благоприятным, если для любого другого распределения средний риск удовлетворяет . π {\displaystyle \pi \,\!} π ′ {\displaystyle \pi '\,\!} r π ≥ r π ′ {\displaystyle r_{\pi }\geq r_{\pi '}\,}

Теорема 1: Если тогда: r π = sup θ R ( θ , δ π ) , {\displaystyle r_{\pi }=\sup _{\theta }R(\theta ,\delta _{\pi }),\,}

  1. δ π {\displaystyle \delta _{\pi }\,\!} является минимаксом.
  2. Если — уникальная байесовская оценка, то она также является уникальной минимаксной оценкой. δ π {\displaystyle \delta _{\pi }\,\!}
  3. π {\displaystyle \pi \,\!} наименее благоприятен.

Следствие: Если байесовский оценщик имеет постоянный риск, он минимаксный. Обратите внимание, что это не необходимое условие.

Пример 1: Нечестная монета [2] [3] : Рассмотрим задачу оценки "успешности" биномиальной переменной, . Это можно рассматривать как оценку скорости, с которой нечестная монета падает "орлом" или "решкой". В этом случае байесовский оценщик относительно бета -распределенного априорного распределения имеет вид x ∼ B ( n , θ ) {\displaystyle x\sim B(n,\theta )\,\!} θ ∼ Beta ( n / 2 , n / 2 ) {\displaystyle \theta \sim {\text{Beta}}({\sqrt {n}}/2,{\sqrt {n}}/2)\,}

δ M = x + 0.5 n n + n , {\displaystyle \delta ^{M}={\frac {x+0.5{\sqrt {n}}}{n+{\sqrt {n}}}},\,}

с постоянным байесовским риском

r = 1 4 ( 1 + n ) 2 {\displaystyle r={\frac {1}{4(1+{\sqrt {n}})^{2}}}\,}

и, согласно Следствию, является минимаксным.

Определение: Последовательность априорных распределений называется наименее благоприятной , если для любого другого распределения π n {\displaystyle \pi _{n}\,\!} π ′ {\displaystyle \pi '\,\!}

lim n → ∞ r π n ≥ r π ′ . {\displaystyle \lim _{n\rightarrow \infty }r_{\pi _{n}}\geq r_{\pi '}.\,}

Теорема 2: Если существует последовательность априорных вероятностей и оценщик такой, что , то: π n {\displaystyle \pi _{n}\,\!} δ {\displaystyle \delta \,\!} sup θ R ( θ , δ ) = lim n → ∞ r π n {\displaystyle \sup _{\theta }R(\theta ,\delta )=\lim _{n\rightarrow \infty }r_{\pi _{n}}\,\!}

  1. δ {\displaystyle \delta \,\!} является минимаксом.
  2. Последовательность наименее благоприятна. π n {\displaystyle \pi _{n}\,\!}

Обратите внимание, что здесь не гарантируется уникальность. Например, оценка ML из предыдущего примера может быть достигнута как предел оценок Байеса относительно равномерного априорного распределения с увеличивающейся поддержкой, а также относительно нормального априорного распределения с нулевым средним с увеличивающейся дисперсией. Таким образом, ни полученная оценка ML не является уникальной минимаксной, ни наименее благоприятная априорная вероятность не является уникальной. π n ∼ U [ − n , n ] {\displaystyle \pi _{n}\sim U[-n,n]\,\!} π n ∼ N ( 0 , n σ 2 ) {\displaystyle \pi _{n}\sim N(0,n\sigma ^{2})\,\!}

Пример 2: Рассмотрим задачу оценки среднего размерного гауссовского случайного вектора, . Оценка максимального правдоподобия (ML) для в этом случае просто , а ее риск равен p {\displaystyle p\,\!} x ∼ N ( θ , I p σ 2 ) {\displaystyle x\sim N(\theta ,I_{p}\sigma ^{2})\,\!} θ {\displaystyle \theta \,\!} δ ML = x {\displaystyle \delta _{\text{ML}}=x\,\!}

R ( θ , δ ML ) = E ‖ δ M L − θ ‖ 2 = ∑ i = 1 p E ( x i − θ i ) 2 = p σ 2 . {\displaystyle R(\theta ,\delta _{\text{ML}})=E{\|\delta _{ML}-\theta \|^{2}}=\sum _{i=1}^{p}E(x_{i}-\theta _{i})^{2}=p\sigma ^{2}.\,}
Среднеквадратическая ошибка оценки максимального правдоподобия в сравнении с оценкой Джеймса–Стейна

Риск постоянен, но оценщик ML на самом деле не является оценщиком Байеса, поэтому следствие теоремы 1 неприменимо. Однако оценщик ML является пределом оценщиков Байеса относительно априорной последовательности , и, следовательно, действительно минимаксным согласно теореме 2. Тем не менее, минимаксность не всегда подразумевает допустимость . Фактически в этом примере известно, что оценщик ML является недопустимым (недопустимым) всякий раз, когда . Знаменитый оценщик Джеймса–Стейна доминирует над ML всякий раз, когда . Хотя оба оценщика имеют одинаковый риск , когда , и оба они являются минимаксными, оценщик Джеймса–Стейна имеет меньший риск для любого конечного . Этот факт проиллюстрирован на следующем рисунке. π n ∼ N ( 0 , n σ 2 ) {\displaystyle \pi _{n}\sim N(0,n\sigma ^{2})\,\!} p > 2 {\displaystyle p>2\,\!} p > 2 {\displaystyle p>2\,\!} p σ 2 {\displaystyle p\sigma ^{2}\,\!} ‖ θ ‖ → ∞ {\displaystyle \|\theta \|\rightarrow \infty \,\!} ‖ θ ‖ {\displaystyle \|\theta \|\,\!}

Некоторые примеры

В общем случае, сложно, часто даже невозможно определить минимаксную оценку. Тем не менее, во многих случаях минимаксная оценка была определена.

Пример 3: Ограниченное нормальное среднее: При оценке среднего нормального вектора , где известно, что . Известно, что байесовская оценка относительно априорной вероятности, которая равномерно распределена на краю ограничивающей сферы , является минимаксной, когда . Аналитическое выражение для этой оценки имеет вид x ∼ N ( θ , I n σ 2 ) {\displaystyle x\sim N(\theta ,I_{n}\sigma ^{2})\,\!} ‖ θ ‖ 2 ≤ M {\displaystyle \|\theta \|^{2}\leq M\,\!} M ≤ n {\displaystyle M\leq n\,\!}

δ M ( x ) = M J n + 1 ( M ‖ x ‖ ) ‖ x ‖ J n ( M ‖ x ‖ ) x , {\displaystyle \delta ^{M}(x)={\frac {MJ_{n+1}(M\|x\|)}{\|x\|J_{n}(M\|x\|)}}x,\,}

где , — модифицированная функция Бесселя первого рода порядка  n . J n ( t ) {\displaystyle J_{n}(t)\,\!}

Асимптотическая минимаксная оценка

Трудность определения точной минимаксной оценки побудила к изучению оценок асимптотического минимакса – оценка называется асимптотическим (или приближенным) минимаксом, если δ ′ {\displaystyle \delta '} c {\displaystyle c}

sup θ ∈ Θ R ( θ , δ ′ ) ≤ c inf δ sup θ ∈ Θ R ( θ , δ ) . {\displaystyle \sup _{\theta \in \Theta }R(\theta ,\delta ')\leq c\inf _{\delta }\sup _{\theta \in \Theta }R(\theta ,\delta ).}

Для многих задач оценки, особенно в непараметрической установке оценки, были установлены различные приближенные минимаксные оценщики. Конструкция приближенного минимаксного оценщика тесно связана с геометрией, такой как метрическое энтропийное число, . Θ {\displaystyle \Theta }

Рандомизированная минимаксная оценка

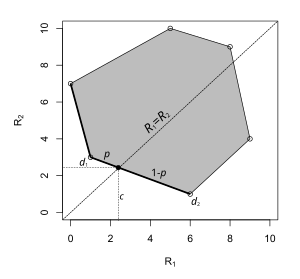
Иногда минимаксная оценка может принимать форму рандомизированного решающего правила . Пример показан слева. Пространство параметров имеет всего два элемента, и каждая точка на графике соответствует риску решающего правила: x-координата является риском, когда параметр равен , а y-координата является риском, когда параметр равен . В этой задаче принятия решения минимаксная оценка лежит на отрезке прямой, соединяющем две детерминированные оценки. Выбор с вероятностью и с вероятностью минимизирует супремум-риск. θ 1 {\displaystyle \theta _{1}} θ 2 {\displaystyle \theta _{2}} δ 1 {\displaystyle \delta _{1}} 1 − p {\displaystyle 1-p} δ 2 {\displaystyle \delta _{2}} p {\displaystyle p}

Связь с надежной оптимизацией

Надежная оптимизация — это подход к решению задач оптимизации в условиях неопределенности в знании базовых параметров. [4] [5] Например, байесовская оценка параметра MMSE требует знания функции корреляции параметра. Если знание этой функции корреляции не полностью доступно, популярный подход минимаксной надежной оптимизации [6] заключается в определении набора, характеризующего неопределенность относительно функции корреляции, а затем проведении минимаксной оптимизации по набору неопределенности и оценщику соответственно. Аналогичные минимаксные оптимизации могут быть проведены для того, чтобы сделать оценщики надежными к определенным неточно известным параметрам. Например, недавнее исследование, посвященное таким методам в области обработки сигналов, можно найти в. [7]

В работе R. Fandom Noubiap и W. Seidel (2001) был разработан алгоритм вычисления решающего правила Gamma-minimax, когда Gamma задается конечным числом обобщенных моментных условий. Такое решающее правило минимизирует максимум интегралов функции риска относительно всех распределений в Gamma. Решающие правила Gamma-minimax представляют интерес для исследований надежности в байесовской статистике.

Ссылки

  • EL Lehmann и G. Casella (1998), Теория точечной оценки, 2-е изд. Нью-Йорк: Springer-Verlag.
  • Ф. Перрон и Э. Маршан (2002), «О минимаксной оценке ограниченного нормального среднего», Statistics and Probability Letters 58 : 327–333.
  • Р. Фэндом Нубиап и В. Зайдель (2001), «Алгоритм для вычисления правил принятия решений гамма-минимакс при обобщенных моментных условиях», Annals of Statistics , август 2001 г., т. 29, № 4, стр. 1094–1116
  • Stein, C. (1981). «Оценка среднего значения многомерного нормального распределения». Annals of Statistics . 9 (6): 1135–1151. doi : 10.1214/aos/1176345632 . MR  0630098. Zbl  0476.62035.
  1. ^ Бергер, Дж. О. (1985). Статистическая теория принятия решений и байесовский анализ (2-е изд.). Нью-Йорк: Springer-Verlag . С. xv+425. ISBN 0-387-96098-8. МР  0580664.
  2. ^ Ходжес, младший, Дж. Л.; Леманн, Э. Л. (1950). «Некоторые проблемы минимаксной оценки точек». Ann. Math. Statist . 21 (2): 182–197. doi : 10.1214/aoms/1177729838 . JSTOR  2236900. MR  0035949. Zbl  0038.09802.
  3. ^ Штайнхаус, Хьюгон (1957). «Проблема оценки». Энн. Математика. Статист . 28 (3): 633–648. дои : 10.1214/aoms/1177706876 . JSTOR  2237224. MR  0092313. Збл  0088.35503.
  4. ^ SA Kassam и HV Poor (1985), «Надежные методы обработки сигналов: обзор», Труды IEEE , т. 73, стр. 433–481, март 1985 г.
  5. ^ А. Бен-Тал, Л. Эль Гауи и А. Немировски (2009), «Надежная оптимизация», Princeton University Press, 2009.
  6. ^ S. Verdu и HV Poor (1984), «О минимаксной надежности: общий подход и приложения», IEEE Transactions on Information Theory , т. 30, стр. 328–340, март 1984 г.
  7. ^ М. Даниш Нисар. Минимаксная надежность в обработке сигналов для связи, Shaker Verlag, ISBN 978-3-8440-0332-1 , август 2011 г. 
Retrieved from "https://en.wikipedia.org/w/index.php?title=Minimax_estimator&oldid=1043045020"