Оптика

| Часть серии статей о |
| Физика |
|---|
 |
|
Оптика — это раздел физики , изучающий поведение и свойства света , включая его взаимодействие с материей и создание инструментов , которые используют или обнаруживают его. [1] Оптика обычно описывает поведение видимого , ультрафиолетового и инфракрасного света. Свет — это тип электромагнитного излучения , а другие формы электромагнитного излучения, такие как рентгеновские лучи , микроволны и радиоволны, обладают схожими свойствами. [1]
Большинство оптических явлений можно объяснить с помощью классического электромагнитного описания света, однако полные электромагнитные описания света часто трудно применять на практике. Практическая оптика обычно выполняется с использованием упрощенных моделей. Наиболее распространенная из них, геометрическая оптика , рассматривает свет как совокупность лучей , которые движутся по прямым линиям и изгибаются при прохождении через поверхности или отражении от них. Физическая оптика — более полная модель света, которая включает волновые эффекты, такие как дифракция и интерференция , которые нельзя объяснить в геометрической оптике. Исторически сначала была разработана лучевая модель света, а затем волновая модель света. Прогресс в электромагнитной теории в 19 веке привел к открытию того, что световые волны на самом деле являются электромагнитным излучением.
Некоторые явления зависят от света, имеющего как волновые, так и корпускулярные свойства . Объяснение этих эффектов требует квантовой механики . При рассмотрении корпускулярных свойств света свет моделируется как совокупность частиц, называемых « фотонами ». Квантовая оптика занимается применением квантовой механики к оптическим системам.
Оптическая наука имеет отношение и изучается во многих смежных дисциплинах, включая астрономию , различные области техники , фотографию и медицину (особенно офтальмологию и оптометрию , в которых она называется физиологической оптикой). Практическое применение оптики можно найти в различных технологиях и повседневных предметах, включая зеркала , линзы , телескопы , микроскопы , лазеры и волоконную оптику .
История

Оптика началась с разработки линз древними египтянами и жителями Месопотамии . Самые ранние известные линзы, сделанные из полированного кристалла , часто кварца , датируются еще 2000 годом до нашей эры на Крите (Археологический музей Ираклиона, Греция). Линзы с Родоса датируются примерно 700 годом до нашей эры, как и ассирийские линзы, такие как линза Нимруда . [2] Древние римляне и греки заполняли стеклянные сферы водой, чтобы сделать линзы. За этими практическими разработками последовало развитие теорий света и зрения древнегреческими и индийскими философами , а также развитие геометрической оптики в греко-римском мире . Слово оптика происходит от древнегреческого слова ὀπτική , optikē ' внешний вид, взгляд ' . [3]
Греческая философия оптики распалась на две противоположные теории о том, как работает зрение, теорию интромиссии и теорию эмиссии . [4] Подход интромиссии рассматривал зрение как результат того, что объекты отбрасывают копии себя (называемые эйдолами), которые улавливаются глазом. Со многими пропагандистами, включая Демокрита , Эпикура , Аристотеля и их последователей, эта теория, кажется, имеет некоторую связь с современными теориями о том, что такое зрение на самом деле, но она оставалась только предположением, лишенным какой-либо экспериментальной основы.
Платон первым сформулировал теорию эмиссии , идею о том, что зрительное восприятие осуществляется лучами, испускаемыми глазами. Он также прокомментировал изменение четности зеркал в «Тимее» . [5] Несколько сотен лет спустя Евклид (IV–III вв. до н. э.) написал трактат под названием «Оптика» , где связал зрение с геометрией , создав геометрическую оптику . [6] Он основывал свою работу на теории эмиссии Платона, в которой он описал математические правила перспективы и качественно описал эффекты преломления , хотя он сомневался, что луч света из глаза может мгновенно освещать звезды каждый раз, когда кто-то моргает. [7] Евклид сформулировал принцип кратчайшей траектории света и рассмотрел множественные отражения от плоских и сферических зеркал. Птолемей в своем трактате «Оптика» придерживался экстрамиссионной-интромиссионной теории зрения: лучи (или поток) из глаза образовывали конус, вершина которого находилась внутри глаза, а основание определяло поле зрения. Лучи были чувствительны и передавали информацию обратно в интеллект наблюдателя о расстоянии и ориентации поверхностей. Он обобщил большую часть Евклида и продолжил описывать способ измерения угла преломления , хотя он не заметил эмпирической связи между ним и углом падения. [8] Плутарх (I–II вв. н. э.) описал множественные отражения на сферических зеркалах и обсуждал создание увеличенных и уменьшенных изображений, как реальных, так и мнимых, включая случай хиральности изображений.
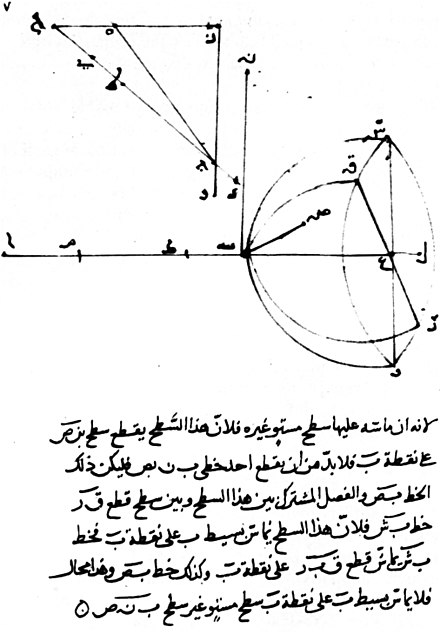
В Средние века греческие идеи об оптике были возрождены и расширены писателями в мусульманском мире . Одним из первых из них был Аль-Кинди ( ок. 801–873 ), который писал о достоинствах идей Аристотеля и Евклида об оптике, отдавая предпочтение теории излучения, поскольку она могла лучше количественно оценить оптические явления. [9] В 984 году персидский математик Ибн Сахл написал трактат «О зажигательных зеркалах и линзах», правильно описав закон преломления, эквивалентный закону Снеллиуса. [10] Он использовал этот закон для вычисления оптимальных форм для линз и изогнутых зеркал . В начале 11 века Альхазен (Ибн аль-Хайтам) написал « Книгу оптики» ( Китаб аль-маназир ), в которой он исследовал отражение и преломление и предложил новую систему для объяснения зрения и света на основе наблюдения и эксперимента. [11] Он отверг «теорию излучения» оптики Птолемея, согласно которой лучи испускаются глазом, и вместо этого выдвинул идею о том, что свет отражается во всех направлениях по прямым линиям от всех точек рассматриваемых объектов, а затем входит в глаз, хотя он не смог правильно объяснить, как глаз улавливает лучи. [12] Работа Альхазена была в значительной степени проигнорирована в арабском мире, но была анонимно переведена на латынь около 1200 г. н.э. и далее обобщена и расширена польским монахом Витело [13], что сделало ее стандартным текстом по оптике в Европе на следующие 400 лет. [14]
В XIII веке в средневековой Европе английский епископ Роберт Гроссетест писал по широкому кругу научных тем и обсуждал свет с четырех различных точек зрения: эпистемология света, метафизика или космогония света, этиология или физика света и теология света, [15] основываясь на трудах Аристотеля и платонизма. Самый известный ученик Гроссетеста, Роджер Бэкон , написал работы, ссылаясь на широкий спектр недавно переведенных оптических и философских трудов, включая работы Альхазена, Аристотеля, Авиценны , Аверроэса , Евклида, аль-Кинди, Птолемея, Тидея и Константина Африканского . Бэкон смог использовать части стеклянных сфер в качестве увеличительных стекол , чтобы продемонстрировать, что свет отражается от объектов, а не испускается ими.
Первые носимые очки были изобретены в Италии около 1286 года. [16] Это было началом оптической промышленности по шлифовке и полировке линз для этих «очков», сначала в Венеции и Флоренции в тринадцатом веке, [17] а затем в центрах по производству очков как в Нидерландах, так и в Германии. [18] Производители очков создали улучшенные типы линз для коррекции зрения, основанные больше на эмпирических знаниях, полученных при наблюдении за эффектами линз, а не на использовании элементарной оптической теории того времени (теории, которая по большей части не могла даже адекватно объяснить, как работают очки). [19] [20] Это практическое развитие, мастерство и эксперименты с линзами привели непосредственно к изобретению составного оптического микроскопа около 1595 года и рефракционного телескопа в 1608 году, оба из которых появились в центрах по производству очков в Нидерландах. [21] [22]



В начале 17 века Иоганн Кеплер расширил геометрическую оптику в своих трудах, охватывая линзы, отражение плоскими и изогнутыми зеркалами, принципы камер-обскуры , закон обратных квадратов, управляющий интенсивностью света, и оптические объяснения астрономических явлений, таких как лунные и солнечные затмения и астрономический параллакс . Он также смог правильно вывести роль сетчатки как фактического органа, который регистрирует изображения, наконец, сумев научно количественно оценить эффекты различных типов линз, которые производители очков наблюдали в течение предыдущих 300 лет. [24] После изобретения телескопа Кеплер изложил теоретическую основу того, как они работали, и описал улучшенную версию, известную как телескоп Кеплера , в которой использовались две выпуклые линзы для получения большего увеличения. [25]
Оптическая теория развивалась в середине 17 века с трактатами , написанными философом Рене Декартом , который объяснял множество оптических явлений, включая отражение и преломление, предполагая, что свет испускается объектами, которые его производят. [26] Это существенно отличалось от древнегреческой теории излучения. В конце 1660-х и начале 1670-х годов Исаак Ньютон расширил идеи Декарта до корпускулярной теории света , определив, что белый свет представляет собой смесь цветов, которые можно разделить на составные части с помощью призмы . В 1690 году Христиан Гюйгенс предложил волновую теорию света, основанную на предложениях, высказанных Робертом Гуком в 1664 году. Сам Гук публично критиковал теории света Ньютона, и вражда между ними продолжалась до самой смерти Гука. В 1704 году Ньютон опубликовал «Оптику» , и в то время, отчасти из-за его успехов в других областях физики, его обычно считали победителем в споре о природе света. [26]
Ньютоновская оптика была общепринятой до начала 19 века, когда Томас Юнг и Огюстен-Жан Френель провели эксперименты по интерференции света, которые твердо установили волновую природу света. Знаменитый эксперимент Юнга с двумя щелями показал, что свет следует принципу суперпозиции , который является волновым свойством, не предсказанным теорией корпускул Ньютона. Эта работа привела к теории дифракции света и открыла целую область исследований в физической оптике. [27] Волновая оптика была успешно объединена с электромагнитной теорией Джеймсом Клерком Максвеллом в 1860-х годах. [28]
Следующее развитие оптической теории произошло в 1899 году, когда Макс Планк правильно смоделировал излучение черного тела , предположив, что обмен энергией между светом и материей происходит только в дискретных количествах, которые он назвал квантами . [29] В 1905 году Альберт Эйнштейн опубликовал теорию фотоэлектрического эффекта , которая прочно установила квантование самого света. [30] [31] В 1913 году Нильс Бор показал, что атомы могут излучать только дискретные количества энергии, тем самым объяснив дискретные линии, видимые в спектрах излучения и поглощения . [32] Понимание взаимодействия между светом и материей, которое последовало из этих разработок, не только легло в основу квантовой оптики, но и имело решающее значение для развития квантовой механики в целом. Конечная кульминация, теория квантовой электродинамики , объясняет всю оптику и электромагнитные процессы в целом как результат обмена реальными и виртуальными фотонами. [33] Квантовая оптика приобрела практическое значение с изобретением мазера в 1953 году и лазера в 1960 году. [34]
После работ Поля Дирака по квантовой теории поля Джордж Сударшан , Рой Дж. Глаубер и Леонард Мандель в 1950-х и 1960-х годах применили квантовую теорию к электромагнитному полю, чтобы получить более детальное представление о фотодетектировании и статистике света.
Классическая оптика

Классическая оптика делится на две основные ветви: геометрическую (или лучевую) оптику и физическую (или волновую) оптику. В геометрической оптике считается, что свет распространяется по прямым линиям, тогда как в физической оптике свет рассматривается как электромагнитная волна.
Геометрическую оптику можно рассматривать как приближение физической оптики, применяемое в случаях, когда длина волны используемого света намного меньше размера оптических элементов в моделируемой системе.
Геометрическая оптика

Геометрическая оптика , или лучевая оптика , описывает распространение света в терминах «лучей», которые движутся по прямым линиям, и чьи пути управляются законами отражения и преломления на границах раздела различных сред. [35] Эти законы были открыты эмпирическим путем еще в 984 году нашей эры [10] и использовались при проектировании оптических компонентов и приборов с тех пор и до наших дней. Их можно обобщить следующим образом:
Когда луч света попадает на границу между двумя прозрачными материалами, он разделяется на отраженный и преломленный луч.
- Закон отражения гласит, что отраженный луч лежит в плоскости падения, а угол отражения равен углу падения.
- Закон преломления гласит, что преломленный луч лежит в плоскости падения, а синус угла падения, деленный на синус угла преломления, является константой: где n — константа для любых двух материалов и данного цвета света. Если первый материал — воздух или вакуум, n — показатель преломления второго материала.
Законы отражения и преломления можно вывести из принципа Ферма , который гласит, что путь, пройденный лучом света между двумя точками, — это путь, который можно пройти за наименьшее время. [36]
Приближения
Геометрическая оптика часто упрощается путем создания параксиального приближения или «приближения малого угла». Математическое поведение затем становится линейным, что позволяет описывать оптические компоненты и системы простыми матрицами. Это приводит к методам гауссовой оптики и параксиальной трассировки лучей , которые используются для нахождения основных свойств оптических систем, таких как приблизительное изображение и положение объекта и увеличение . [37]
Размышления

Отражения можно разделить на два типа: зеркальное отражение и диффузное отражение . Зеркальное отражение описывает блеск поверхностей, таких как зеркала, которые отражают свет простым, предсказуемым образом. Это позволяет создавать отраженные изображения, которые можно связать с фактическим ( реальным ) или экстраполированным ( виртуальным ) местоположением в пространстве. Диффузное отражение описывает неглянцевые материалы, такие как бумага или камень. Отражения от этих поверхностей можно описать только статистически, с точным распределением отраженного света в зависимости от микроскопической структуры материала. Многие диффузные отражатели описываются или могут быть аппроксимированы законом косинуса Ламберта , который описывает поверхности, имеющие одинаковую яркость при просмотре под любым углом. Глянцевые поверхности могут давать как зеркальное, так и диффузное отражение.
При зеркальном отражении направление отраженного луча определяется углом, который падающий луч образует с нормалью к поверхности , линией, перпендикулярной поверхности в точке, куда падает луч. Падающий и отраженный лучи и нормаль лежат в одной плоскости, а угол между отраженным лучом и нормалью к поверхности такой же, как угол между падающим лучом и нормалью. [38] Это известно как Закон отражения .
Для плоских зеркал закон отражения подразумевает, что изображения объектов являются вертикальными и находятся на том же расстоянии позади зеркала, что и объекты перед зеркалом. Размер изображения такой же, как и размер объекта. Закон также подразумевает, что зеркальные изображения являются инвертированными по четности, что мы воспринимаем как инверсию лево-право. Изображения, сформированные при отражении в двух (или любом четном числе) зеркалах, не являются инвертированными по четности. Угловые отражатели создают отраженные лучи, которые движутся обратно в направлении, откуда пришли падающие лучи. [39] Это называется ретрорефлексией .
Зеркала с изогнутыми поверхностями можно моделировать с помощью трассировки лучей и использования закона отражения в каждой точке поверхности. Для зеркал с параболическими поверхностями параллельные лучи, падающие на зеркало, создают отраженные лучи, которые сходятся в общем фокусе . Другие изогнутые поверхности также могут фокусировать свет, но с аберрациями из-за расходящейся формы, заставляющей фокус размываться в пространстве. В частности, сферические зеркала демонстрируют сферическую аберрацию . Изогнутые зеркала могут формировать изображения с увеличением больше или меньше единицы, и увеличение может быть отрицательным, что указывает на то, что изображение перевернуто. Прямое изображение, сформированное отражением в зеркале, всегда является виртуальным, в то время как перевернутое изображение является реальным и может быть спроецировано на экран. [40]
Преломления

Рефракция происходит, когда свет проходит через область пространства с изменяющимся показателем преломления; этот принцип допускает линзы и фокусировку света. Простейший случай рефракции происходит, когда есть интерфейс между однородной средой с показателем преломления n 1 и другой средой с показателем преломления n 2 . В таких ситуациях закон Снеллиуса описывает результирующее отклонение светового луча:
где θ 1 и θ 2 — углы между нормалью (к границе раздела) и падающей и преломленной волнами соответственно. [38]
Показатель преломления среды связан со скоростью света v в этой среде соотношением, где c — скорость света в вакууме .
Закон Снеллиуса можно использовать для прогнозирования отклонения световых лучей при их прохождении через линейные среды, если известны показатели преломления и геометрия среды. Например, распространение света через призму приводит к отклонению светового луча в зависимости от формы и ориентации призмы. В большинстве материалов показатель преломления изменяется в зависимости от частоты света, известной как дисперсия . Принимая это во внимание, закон Снеллиуса можно использовать для прогнозирования того, как призма будет рассеивать свет в спектр. [41] Открытие этого явления при прохождении света через призму приписывается Исааку Ньютону.
Некоторые среды имеют показатель преломления, который постепенно меняется в зависимости от положения, и поэтому световые лучи в среде искривляются. Этот эффект отвечает за миражи , наблюдаемые в жаркие дни: изменение показателя преломления воздуха с высотой заставляет световые лучи изгибаться, создавая видимость зеркальных отражений на расстоянии (как на поверхности бассейна с водой). Оптические материалы с переменным показателем преломления называются материалами с градиентным показателем преломления (GRIN). Такие материалы используются для изготовления оптики с градиентным показателем преломления . [42]
Для световых лучей, идущих от материала с высоким показателем преломления к материалу с низким показателем преломления, закон Снеллиуса предсказывает, что нет θ 2, когда θ 1 велико. В этом случае передача не происходит; весь свет отражается. Это явление называется полным внутренним отражением и позволяет использовать технологию волоконной оптики. Когда свет проходит по оптоволокну, он претерпевает полное внутреннее отражение, что позволяет практически не терять свет по всей длине кабеля. [43]
Линзы

Устройство, которое производит сходящиеся или расходящиеся световые лучи из-за преломления, известно как линза . Линзы характеризуются своим фокусным расстоянием : собирательная линза имеет положительное фокусное расстояние, в то время как рассеивающая линза имеет отрицательное фокусное расстояние. Меньшее фокусное расстояние указывает на то, что линза имеет более сильный собирательный или расходящийся эффект. Фокусное расстояние простой линзы в воздухе определяется уравнением изготовителя линз . [44]
Трассировка лучей может быть использована для того, чтобы показать, как линза формирует изображения. Для тонкой линзы в воздухе местоположение изображения задается простым уравнением
где S 1 — расстояние от объекта до линзы, θ 2 — расстояние от линзы до изображения, а f — фокусное расстояние линзы. В используемом здесь соглашении о знаках расстояния до объекта и изображения положительны, если объект и изображение находятся по разные стороны линзы. [45]

Входящие параллельные лучи фокусируются собирательной линзой в точку, находящуюся на расстоянии одного фокусного расстояния от линзы, на дальней стороне линзы. Это называется задней фокусной точкой линзы. Лучи от объекта, находящегося на конечном расстоянии, фокусируются дальше от линзы, чем фокусное расстояние; чем ближе объект к линзе, тем дальше от линзы находится изображение.
В рассеивающих линзах входящие параллельные лучи расходятся после прохождения через линзу таким образом, что кажется, что они возникли в точке, расположенной на расстоянии одного фокусного расстояния перед линзой. Это передняя фокусная точка линзы. Лучи от объекта на конечном расстоянии связаны с мнимым изображением, которое находится ближе к линзе, чем фокусная точка, и с той же стороны линзы, что и объект. Чем ближе объект к линзе, тем ближе мнимое изображение к линзе. Как и в случае с зеркалами, прямые изображения, создаваемые одной линзой, являются мнимыми, а перевернутые изображения — действительными. [46]
Линзы страдают от аберраций , которые искажают изображения. Монохроматические аберрации возникают из-за того, что геометрия линзы не идеально направляет лучи от каждой точки объекта в одну точку на изображении, в то время как хроматическая аберрация возникает из-за того, что показатель преломления линзы изменяется в зависимости от длины волны света. [47]

Физическая оптика
В физической оптике считается, что свет распространяется в виде волн. Эта модель предсказывает такие явления, как интерференция и дифракция, которые не объясняются геометрической оптикой. Скорость световых волн в воздухе составляет приблизительно 3,0×10 8 м/с (ровно 299 792 458 м/с в вакууме ). Длина волны видимых световых волн варьируется от 400 до 700 нм, но термин «свет» также часто применяется к инфракрасному (0,7–300 мкм) и ультрафиолетовому излучению (10–400 нм).
Волновая модель может использоваться для прогнозирования поведения оптической системы, не требуя объяснения того, что «колеблется» в какой среде. До середины 19 века большинство физиков верили в «эфирную» среду, в которой распространяется световое возмущение. [48] Существование электромагнитных волн было предсказано в 1865 году уравнениями Максвелла . Эти волны распространяются со скоростью света и имеют переменные электрические и магнитные поля, которые ортогональны друг другу, а также направлению распространения волн. [49] Световые волны в настоящее время обычно рассматриваются как электромагнитные волны, за исключением случаев, когда необходимо учитывать квантово-механические эффекты.
Моделирование и проектирование оптических систем с использованием физической оптики
Для анализа и проектирования оптических систем доступно множество упрощенных приближений. Большинство из них используют одну скалярную величину для представления электрического поля световой волны, а не используют векторную модель с ортогональными электрическими и магнитными векторами. [50] Уравнение Гюйгенса–Френеля является одной из таких моделей. Оно было выведено эмпирически Френелем в 1815 году на основе гипотезы Гюйгенса о том, что каждая точка на волновом фронте генерирует вторичный сферический волновой фронт, который Френель объединил с принципом суперпозиции волн. Уравнение дифракции Кирхгофа , которое выведено с использованием уравнений Максвелла, ставит уравнение Гюйгенса–Френеля на более прочную физическую основу. Примеры применения принципа Гюйгенса–Френеля можно найти в статьях о дифракции и дифракции Фраунгофера .
Более строгие модели, включающие моделирование как электрических, так и магнитных полей световой волны, требуются при работе с материалами, электрические и магнитные свойства которых влияют на взаимодействие света с материалом. Например, поведение световой волны, взаимодействующей с металлической поверхностью, существенно отличается от того, что происходит при ее взаимодействии с диэлектрическим материалом. Векторная модель также должна использоваться для моделирования поляризованного света.
Методы численного моделирования, такие как метод конечных элементов , метод граничных элементов и метод матрицы линии передачи, могут использоваться для моделирования распространения света в системах, которые не могут быть решены аналитически. Такие модели требуют больших вычислительных затрат и обычно используются только для решения задач небольшого масштаба, требующих точности, превышающей ту, которая может быть достигнута с помощью аналитических решений. [51]
Все результаты геометрической оптики можно получить с помощью методов Фурье-оптики , в которых применяются многие из тех же математических и аналитических методов, которые используются в акустической инженерии и обработке сигналов .
Распространение гауссова пучка — это простая параксиальная физическая оптическая модель для распространения когерентного излучения, такого как лазерные лучи. Эта техника частично учитывает дифракцию, позволяя точно рассчитать скорость, с которой лазерный луч расширяется с расстоянием, и минимальный размер, до которого луч может быть сфокусирован. Таким образом, распространение гауссова пучка заполняет разрыв между геометрической и физической оптикой. [52]
Суперпозиция и интерференция
При отсутствии нелинейных эффектов принцип суперпозиции может быть использован для прогнозирования формы взаимодействующих волновых форм посредством простого сложения возмущений. [53] Это взаимодействие волн для создания результирующего рисунка обычно называется «интерференцией» и может привести к различным результатам. Если две волны с одинаковой длиной волны и частотой находятся в фазе , то гребни и впадины волн выравниваются. Это приводит к конструктивной интерференции и увеличению амплитуды волны, что для света связано с усилением яркости волновой формы в этом месте. В качестве альтернативы, если две волны с одинаковой длиной волны и частотой находятся вне фазы, то гребни волн будут выравниваться с впадинами волн и наоборот. Это приводит к деструктивной интерференции и уменьшению амплитуды волны, что для света связано с затемнением волновой формы в этом месте. Ниже приведена иллюстрация этого эффекта. [54]
| комбинированная форма волны |  | |
| волна 1 | ||
| волна 2 | ||
| Две волны в фазе | Две волны, сдвинутые по фазе на 180° | |

Поскольку принцип Гюйгенса-Френеля гласит, что каждая точка волнового фронта связана с созданием нового возмущения, волновой фронт может интерферировать сам с собой конструктивно или деструктивно в разных местах, создавая яркие и темные полосы в регулярных и предсказуемых узорах. [55] Интерферометрия — это наука об измерении этих узоров, обычно как средство точного определения расстояний или угловых разрешений . [56] Интерферометр Майкельсона был известным прибором, который использовал эффекты интерференции для точного измерения скорости света. [57]
Внешний вид тонких пленок и покрытий напрямую зависит от интерференционных эффектов. Антибликовые покрытия используют деструктивную интерференцию для снижения отражательной способности поверхностей, которые они покрывают, и могут использоваться для минимизации бликов и нежелательных отражений. Простейший случай — один слой толщиной в одну четверть длины волны падающего света. Отраженная волна от верхней части пленки и отраженная волна от интерфейса пленка/материал тогда находятся точно в противофазе на 180°, что вызывает деструктивную интерференцию. Волны находятся точно в противофазе только для одной длины волны, которая обычно выбирается близко к центру видимого спектра, около 550 нм. Более сложные конструкции с использованием нескольких слоев могут достичь низкой отражательной способности в широком диапазоне или чрезвычайно низкой отражательной способности на одной длине волны.
Конструктивная интерференция в тонких пленках может создавать сильное отражение света в диапазоне длин волн, который может быть узким или широким в зависимости от конструкции покрытия. Эти пленки используются для изготовления диэлектрических зеркал , интерференционных фильтров , теплоотражателей и фильтров для разделения цветов в цветных телевизионных камерах. Этот эффект интерференции также является причиной появления красочных радужных узоров, наблюдаемых на нефтяных пятнах. [58]
Дифракция и оптическое разрешение

Дифракция — это процесс, при котором интерференция света наблюдается чаще всего. Эффект был впервые описан в 1665 году Франческо Мария Гримальди , который также придумал термин от латинского diffringere « разбивать на части » . [59] [60] Позже в том же столетии Роберт Гук и Исаак Ньютон также описали явления, которые теперь известны как дифракция в кольцах Ньютона [61], в то время как Джеймс Грегори записал свои наблюдения дифракционных картин от перьев птиц. [62]
Первая физическая оптическая модель дифракции, основанная на принципе Гюйгенса-Френеля, была разработана в 1803 году Томасом Юнгом в его экспериментах по интерференции с интерференционными узорами двух близко расположенных щелей. Юнг показал, что его результаты могут быть объяснены только в том случае, если две щели действуют как два уникальных источника волн, а не корпускул. [63] В 1815 и 1818 годах Огюстен-Жан Френель твердо установил математику того, как интерференция волн может объяснить дифракцию. [64]
Простейшие физические модели дифракции используют уравнения, описывающие угловое разделение светлых и темных полос из-за света определенной длины волны ( λ ). В общем случае уравнение имеет вид где d - разделение между двумя источниками волнового фронта (в случае экспериментов Юнга это были две щели ), θ - угловое разделение между центральной полосой и полосой m -го порядка, где центральный максимум равен m = 0. [65 ]
Это уравнение немного изменено, чтобы учесть различные ситуации, такие как дифракция через один зазор, дифракция через несколько щелей или дифракция через дифракционную решетку , которая содержит большое количество щелей на равном расстоянии. [66] Более сложные модели дифракции требуют работы с математикой дифракции Френеля или Фраунгофера . [67]
Рентгеновская дифракция использует тот факт, что атомы в кристалле имеют регулярное расстояние между собой на расстоянии порядка одного ангстрема . Чтобы увидеть дифракционные картины, рентгеновские лучи с длинами волн, близкими к этому расстоянию, пропускаются через кристалл. Поскольку кристаллы являются трехмерными объектами, а не двумерными решетками, соответствующая дифракционная картина изменяется в двух направлениях в соответствии с отражением Брэгга , при этом соответствующие яркие пятна появляются в уникальных узорах , а d является удвоенным расстоянием между атомами. [68]
Дифракционные эффекты ограничивают способность оптического детектора оптически разрешать отдельные источники света. В общем случае, свет, проходящий через апертуру, будет испытывать дифракцию, и наилучшие изображения, которые могут быть созданы (как описано в оптике с ограниченной дифракцией ), выглядят как центральное пятно с окружающими яркими кольцами, разделенными темными нулями; этот узор известен как узор Эйри , а центральный яркий лепесток — как диск Эйри . [69] Размер такого диска определяется выражением, где θ — угловое разрешение, λ — длина волны света, а D — диаметр апертуры линзы. Если угловое разделение двух точек значительно меньше углового радиуса диска Эйри, то две точки не могут быть разрешены на изображении, но если их угловое разделение намного больше этого, формируются отдельные изображения двух точек, и поэтому они могут быть разрешены. Рэлей определил несколько произвольный « критерий Рэлея », согласно которому две точки, угловое разделение которых равно радиусу диска Эйри (измеренному до первого нуля, то есть до первого места, где не видно света), можно считать разрешенными. Можно видеть, что чем больше диаметр линзы или ее апертуры, тем лучше разрешение. [70] Интерферометрия , с ее способностью имитировать чрезвычайно большие базовые апертуры, позволяет получить максимально возможное угловое разрешение. [56]
Для астрономических изображений атмосфера препятствует достижению оптимального разрешения в видимом спектре из-за атмосферного рассеяния и дисперсии, которые заставляют звезды мерцать . Астрономы называют этот эффект качеством астрономического зрения . Методы, известные как адаптивная оптика, использовались для устранения атмосферных помех в изображениях и достижения результатов, которые приближаются к дифракционному пределу. [71]
Дисперсия и рассеяние

Рефракционные процессы происходят в пределе физической оптики, где длина волны света подобна другим расстояниям, как вид рассеяния. Простейшим типом рассеяния является томсоновское рассеяние , которое происходит, когда электромагнитные волны отклоняются отдельными частицами. В пределе томсоновского рассеяния, в котором очевидна волновая природа света, свет рассеивается независимо от частоты, в отличие от комптоновского рассеяния , которое зависит от частоты и является строго квантово-механическим процессом, включающим природу света как частиц. В статистическом смысле упругое рассеяние света многочисленными частицами, намного меньшими, чем длина волны света, является процессом, известным как рэлеевское рассеяние , в то время как аналогичный процесс рассеяния частицами, которые имеют подобную или большую длину волны, известен как рассеяние Ми , при этом эффект Тиндаля является обычно наблюдаемым результатом. Небольшая часть рассеяния света от атомов или молекул может подвергаться комбинационному рассеянию , при котором частота изменяется из-за возбуждения атомов и молекул. Рассеяние Бриллюэна происходит, когда частота света изменяется из-за локальных изменений со временем и движений плотного материала. [72]
Дисперсия возникает, когда разные частоты света имеют разные фазовые скорости , что обусловлено либо свойствами материала ( материальная дисперсия ), либо геометрией оптического волновода ( волноводная дисперсия ). Наиболее знакомая форма дисперсии — это уменьшение показателя преломления с увеличением длины волны, что наблюдается в большинстве прозрачных материалов. Это называется «нормальной дисперсией». Это происходит во всех диэлектрических материалах в диапазонах длин волн, где материал не поглощает свет. [73] В диапазонах длин волн, где среда имеет значительное поглощение, показатель преломления может увеличиваться с длиной волны. Это называется «аномальной дисперсией». [73]
Разделение цветов призмой является примером нормальной дисперсии. На поверхностях призмы закон Снеллиуса предсказывает, что свет, падающий под углом θ к нормали, будет преломляться под углом arcsin(sin ( θ ) / n ) . Таким образом, синий свет, имеющий более высокий показатель преломления, преломляется сильнее, чем красный свет, что приводит к хорошо известному радужному узору. [41]

Материальная дисперсия часто характеризуется числом Аббе , которое дает простую меру дисперсии на основе показателя преломления на трех определенных длинах волн. Волноводная дисперсия зависит от постоянной распространения . [74] Оба вида дисперсии вызывают изменения групповых характеристик волны, особенностей волнового пакета, которые изменяются с той же частотой, что и амплитуда электромагнитной волны. «Групповая дисперсия скорости» проявляется как размытие «огибающей» сигнала излучения и может быть количественно определена с помощью параметра задержки групповой дисперсии:
где v g — групповая скорость. [75] Для однородной среды групповая скорость равна
где n — показатель преломления, а c — скорость света в вакууме. [76] Это дает более простую форму для параметра задержки дисперсии:
Если D меньше нуля, говорят, что среда имеет положительную дисперсию или нормальную дисперсию. Если D больше нуля, среда имеет отрицательную дисперсию . Если световой импульс распространяется через нормально дисперсионную среду, результатом является то, что компоненты с более высокой частотой замедляются больше, чем компоненты с более низкой частотой. Поэтому импульс становится положительно чирпированным или чирпированным вверх , увеличивая свою частоту со временем. Это приводит к тому, что спектр, выходящий из призмы, выглядит так, что красный свет наименее преломлен, а сине-фиолетовый свет наиболее преломлен. И наоборот, если импульс проходит через аномально (отрицательно) дисперсионную среду, компоненты с высокой частотой распространяются быстрее, чем компоненты с более низкой частотой, и импульс становится отрицательно чирпированным или чирпированным вниз , уменьшая свою частоту со временем. [77]
Результатом дисперсии групповой скорости, будь то отрицательная или положительная, в конечном итоге является временное распространение импульса. Это делает управление дисперсией чрезвычайно важным в оптических системах связи на основе оптических волокон , поскольку если дисперсия слишком высока, группа импульсов, представляющих информацию, будет распространяться во времени и сливаться, делая невозможным извлечение сигнала. [75]
Поляризация
Поляризация — это общее свойство волн, которое описывает ориентацию их колебаний. Для поперечных волн, таких как многие электромагнитные волны, она описывает ориентацию колебаний в плоскости, перпендикулярной направлению движения волны. Колебания могут быть ориентированы в одном направлении ( линейная поляризация ), или направление колебаний может вращаться по мере движения волны ( круговая или эллиптическая поляризация ). Круглополяризованные волны могут вращаться вправо или влево по направлению движения, и то, какое из этих двух вращений присутствует в волне, называется хиральностью волны . [78]
Типичный способ рассмотрения поляризации — отслеживание ориентации вектора электрического поля по мере распространения электромагнитной волны. Вектор электрического поля плоской волны можно произвольно разделить на два перпендикулярных компонента, обозначенных x и y (где z указывает направление движения). Форма, очерченная в плоскости xy вектором электрического поля, является фигурой Лиссажу , которая описывает состояние поляризации . [79] На следующих рисунках показаны некоторые примеры эволюции вектора электрического поля (синего цвета) со временем (вертикальные оси) в определенной точке пространства вместе с его компонентами x и y (красным/левым и зеленым/правым) и путем, проложенным вектором в плоскости (фиолетовым): Та же самая эволюция произошла бы, если бы мы смотрели на электрическое поле в определенное время при эволюции точки в пространстве вдоль направления, противоположного распространению.
На самом левом рисунке выше компоненты x и y световой волны находятся в фазе. В этом случае отношение их сил постоянно, поэтому направление электрического вектора (векторной суммы этих двух компонентов) постоянно. Поскольку кончик вектора вычерчивает одну линию в плоскости, этот особый случай называется линейной поляризацией. Направление этой линии зависит от относительных амплитуд двух компонентов. [80]
На среднем рисунке два ортогональных компонента имеют одинаковые амплитуды и сдвинуты по фазе на 90°. В этом случае один компонент равен нулю, когда другой компонент имеет максимальную или минимальную амплитуду. Существует два возможных фазовых соотношения, которые удовлетворяют этому требованию: компонент x может быть на 90° впереди компонента y или на 90° позади компонента y . В этом особом случае электрический вектор описывает окружность в плоскости, поэтому эта поляризация называется круговой поляризацией. Направление вращения в окружности зависит от того, какое из двухфазных соотношений существует, и соответствует правой круговой поляризации и левой круговой поляризации . [81]
Во всех других случаях, когда два компонента либо не имеют одинаковых амплитуд и/или их разность фаз не равна нулю и не кратна 90°, поляризация называется эллиптической поляризацией, поскольку электрический вектор вычерчивает эллипс в плоскости ( эллипс поляризации ). [82] Это показано на рисунке выше справа. Подробная математика поляризации выполняется с использованием исчисления Джонса и характеризуется параметрами Стокса . [83]
Изменение поляризации
Среды, которые имеют разные показатели преломления для разных поляризационных мод, называются двулучепреломляющими . [84] Хорошо известные проявления этого эффекта появляются в оптических волновых пластинах /замедлителях (линейные моды) и во вращении Фарадея / оптическом вращении (круговые моды). [85] Если длина пути в двулучепреломляющей среде достаточна, плоские волны будут выходить из материала с существенно другим направлением распространения из-за преломления. Например, это имеет место в случае макроскопических кристаллов кальцита , которые представляют наблюдателю два смещенных, ортогонально поляризованных изображения того, что просматривается через них. Именно этот эффект обеспечил первое открытие поляризации Эразмом Бартолинусом в 1669 году. Кроме того, фазовый сдвиг и, следовательно, изменение состояния поляризации обычно зависят от частоты, что в сочетании с дихроизмом часто приводит к появлению ярких цветов и радужных эффектов. В минералогии такие свойства, известные как плеохроизм , часто используются для идентификации минералов с помощью поляризационных микроскопов. Кроме того, многие пластики, которые обычно не являются двупреломляющими, станут таковыми при воздействии механического напряжения , явления, которое является основой фотоупругости . [86] Недвупреломляющие методы, для поворота линейной поляризации световых пучков, включают использование призматических поляризационных ротаторов , которые используют полное внутреннее отражение в наборе призм, разработанном для эффективной коллинеарной передачи. [87]

Среды, которые уменьшают амплитуду определенных поляризационных мод, называются дихроичными , а устройства, которые блокируют почти все излучение в одной моде, называются поляризационными фильтрами или просто « поляризаторами ». Закон Малуса, названный в честь Этьена-Луи Малуса , гласит, что когда идеальный поляризатор помещается в линейно поляризованный луч света, интенсивность, I , проходящего света определяется выражением
где I 0 — начальная интенсивность, а θ i — угол между начальным направлением поляризации света и осью поляризатора. [88]
Луч неполяризованного света можно рассматривать как содержащий однородную смесь линейных поляризаций под всеми возможными углами. Поскольку среднее значение cos 2 θ равно 1/2, коэффициент пропускания становится
На практике часть света теряется в поляризаторе, и фактическое пропускание неполяризованного света будет несколько ниже, около 38% для поляризаторов типа Polaroid, но значительно выше (>49,9%) для некоторых типов двулучепреломляющих призм. [89]
В дополнение к двулучепреломлению и дихроизму в протяженных средах, эффекты поляризации могут также возникать на (отражающем) интерфейсе между двумя материалами с разным показателем преломления. Эти эффекты рассматриваются уравнениями Френеля . Часть волны передается, а часть отражается, причем соотношение зависит от угла падения и угла преломления. Таким образом, физическая оптика восстанавливает угол Брюстера . [90] Когда свет отражается от тонкой пленки на поверхности, интерференция между отражениями от поверхностей пленки может вызывать поляризацию в отраженном и проходящем свете.
Естественное освещение

Большинство источников электромагнитного излучения содержат большое количество атомов или молекул, которые излучают свет. Ориентация электрических полей, создаваемых этими излучателями, может быть некоррелированной , в этом случае свет считается неполяризованным . Если между излучателями существует частичная корреляция, свет частично поляризован . Если поляризация постоянна по всему спектру источника, частично поляризованный свет можно описать как суперпозицию полностью неполяризованного компонента и полностью поляризованного. Тогда можно описать свет в терминах степени поляризации и параметров эллипса поляризации. [79]
Свет, отраженный блестящими прозрачными материалами, частично или полностью поляризован, за исключением случаев, когда свет нормален (перпендикулярен) к поверхности. Именно этот эффект позволил математику Этьену-Луи Малю провести измерения, которые позволили ему разработать первые математические модели для поляризованного света. Поляризация происходит, когда свет рассеивается в атмосфере . Рассеянный свет создает яркость и цвет в ясном небе . Эту частичную поляризацию рассеянного света можно использовать, используя поляризационные фильтры, чтобы затемнить небо на фотографиях . Оптическая поляризация имеет принципиальное значение в химии из-за кругового дихроизма и оптического вращения ( кругового двойного лучепреломления ), проявляемых оптически активными ( хиральными ) молекулами . [91]
Современная оптика
Современная оптика охватывает области оптической науки и техники, которые стали популярными в 20 веке. Эти области оптической науки обычно связаны с электромагнитными или квантовыми свойствами света, но включают и другие темы. Основная область современной оптики, квантовая оптика , занимается конкретно квантово-механическими свойствами света. Квантовая оптика не просто теоретическая; некоторые современные устройства, такие как лазеры, имеют принципы работы, которые зависят от квантовой механики. Детекторы света, такие как фотоумножители и каналотроны , реагируют на отдельные фотоны. Электронные датчики изображения , такие как ПЗС , демонстрируют дробовой шум, соответствующий статистике отдельных фотонных событий. Светодиоды и фотогальванические элементы также не могут быть поняты без квантовой механики. При изучении этих устройств квантовая оптика часто пересекается с квантовой электроникой . [92]
Специальные области оптических исследований включают изучение того, как свет взаимодействует с определенными материалами, как в кристаллической оптике и метаматериалах . Другие исследования фокусируются на феноменологии электромагнитных волн, как в сингулярной оптике , невизуальной оптике , нелинейной оптике , статистической оптике и радиометрии . Кроме того, компьютерные инженеры проявили интерес к интегрированной оптике , машинному зрению и фотонным вычислениям как возможным компонентам «следующего поколения» компьютеров. [93]
Сегодня чистая наука оптика называется оптической наукой или оптической физикой, чтобы отличать ее от прикладных оптических наук, которые называются оптической инженерией . Известные подотрасли оптической инженерии включают светотехнику , фотонику и оптоэлектронику с практическими приложениями, такими как проектирование линз , изготовление и тестирование оптических компонентов и обработка изображений . Некоторые из этих областей пересекаются, с нечеткими границами между терминами субъектов, которые означают немного разные вещи в разных частях мира и в разных областях промышленности. Профессиональное сообщество исследователей нелинейной оптики развилось за последние несколько десятилетий благодаря достижениям в области лазерной технологии. [94]
Лазеры

Лазер — это устройство, которое излучает свет, своего рода электромагнитное излучение, посредством процесса, называемого вынужденным излучением . Термин «лазер» является аббревиатурой от « Усиление света с помощью вынужденного излучения » . [95] Лазерный свет обычно пространственно когерентен , что означает, что свет либо излучается в виде узкого луча с низкой расходимостью , либо может быть преобразован в него с помощью оптических компонентов, таких как линзы. Поскольку микроволновый эквивалент лазера, мазер , был разработан первым, устройства, которые излучают микроволновые и радиочастоты, обычно называются мазерами . [96]

Первый работающий лазер был продемонстрирован 16 мая 1960 года Теодором Майманом в исследовательской лаборатории Хьюза . [98] Когда они были впервые изобретены, их называли «решением, ищущим проблему». [99] С тех пор лазеры стали многомиллиардной индустрией, находящей применение в тысячах самых разнообразных приложений. Первым применением лазеров, заметным в повседневной жизни населения, был сканер штрих-кодов в супермаркете , представленный в 1974 году. [100] Проигрыватель лазерных дисков , представленный в 1978 году, был первым успешным потребительским товаром, включающим лазер, но проигрыватель компакт-дисков был первым устройством, оснащенным лазером, которое стало по-настоящему распространенным в домах потребителей, начиная с 1982 года. [101] Эти оптические запоминающие устройства используют полупроводниковый лазер шириной менее миллиметра для сканирования поверхности диска для извлечения данных. Волоконно-оптическая связь основана на лазерах для передачи больших объемов информации со скоростью света. Другие распространенные применения лазеров включают лазерные принтеры и лазерные указки . Лазеры используются в медицине в таких областях, как бескровная хирургия , лазерная хирургия глаза и лазерная захватная микродиссекция , а также в военных приложениях, таких как системы противоракетной обороны , электрооптические контрмеры (EOCM) и лидары . Лазеры также используются в голограммах , баблграммах , лазерных световых шоу и лазерной эпиляции . [102]
Эффект Капицы–Дирака
Эффект Капицы –Дирака заставляет пучки частиц дифрагировать в результате встречи со стоячей волной света. Свет может быть использован для позиционирования материи с помощью различных явлений (см. оптический пинцет ).
Приложения
Оптика является частью повседневной жизни. Повсеместность зрительных систем в биологии указывает на центральную роль, которую оптика играет как наука об одном из пяти чувств . Многие люди пользуются очками или контактными линзами , а оптика является неотъемлемой частью функционирования многих потребительских товаров, включая камеры . Радуги и миражи являются примерами оптических явлений. Оптическая связь является основой как Интернета , так и современной телефонии .
Человеческий глаз


Человеческий глаз функционирует, фокусируя свет на слое фоторецепторных клеток , называемых сетчаткой, которая образует внутреннюю оболочку задней части глаза. Фокусировка осуществляется серией прозрачных сред. Свет, попадающий в глаз, сначала проходит через роговицу, которая обеспечивает большую часть оптической силы глаза. Затем свет продолжается через жидкость сразу за роговицей — переднюю камеру , затем проходит через зрачок . Затем свет проходит через линзу , которая фокусирует свет дальше и позволяет регулировать фокус. Затем свет проходит через основную часть жидкости в глазу — стекловидное тело , и достигает сетчатки. Клетки в сетчатке выстилают заднюю часть глаза, за исключением места, где выходит зрительный нерв; это приводит к слепому пятну .
Существует два типа фоторецепторных клеток, палочки и колбочки, которые чувствительны к различным аспектам света. [103] Палочковые клетки чувствительны к интенсивности света в широком диапазоне частот, поэтому отвечают за черно-белое зрение . Палочковые клетки отсутствуют в центральной ямке, области сетчатки, отвечающей за центральное зрение, и не так чувствительны, как колбочки, к пространственным и временным изменениям света. Однако в сетчатке палочковых клеток в двадцать раз больше, чем колбочек, поскольку палочковые клетки присутствуют в более широкой области. Из-за их более широкого распространения палочки отвечают за периферическое зрение . [104]
Напротив, колбочки менее чувствительны к общей интенсивности света, но бывают трех видов, которые чувствительны к разным частотным диапазонам и, таким образом, используются в восприятии цвета и фотопическом зрении . Колбочки сильно сконцентрированы в фовеа и имеют высокую остроту зрения, что означает, что они лучше в пространственном разрешении, чем палочки. Поскольку колбочки не так чувствительны к тусклому свету, как палочки, большая часть ночного зрения ограничивается палочками. Аналогично, поскольку колбочки находятся в фовеа, центральное зрение (включая зрение, необходимое для чтения, мелкой детализации, такой как шитье или тщательное изучение объектов) осуществляется колбочками. [104]
Ресничные мышцы вокруг хрусталика позволяют регулировать фокусировку глаза. Этот процесс известен как аккомодация . Ближняя и дальняя точки определяют ближайшее и самое дальнее расстояние от глаза, на котором объект может быть сфокусирован. Для человека с нормальным зрением дальняя точка расположена на бесконечности. Расположение ближней точки зависит от того, насколько мышцы могут увеличить кривизну хрусталика и насколько негибким он стал с возрастом. Оптометристы , офтальмологи и оптики обычно считают подходящей ближней точкой расстояние ближе, чем обычное расстояние для чтения — примерно 25 см. [103]
Дефекты зрения можно объяснить с помощью оптических принципов. С возрастом хрусталик становится менее гибким, а ближняя точка отдаляется от глаза, состояние, известное как пресбиопия . Аналогично, люди, страдающие гиперметропией, не могут уменьшить фокусное расстояние своего хрусталика достаточно, чтобы позволить близким объектам быть отображенными на сетчатке. И наоборот, люди, которые не могут увеличить фокусное расстояние своего хрусталика достаточно, чтобы позволить далеким объектам быть отображенными на сетчатке, страдают миопией и имеют дальнюю точку, которая значительно ближе бесконечности. Состояние, известное как астигматизм, возникает, когда роговица не сферическая, а вместо этого более изогнута в одном направлении. Это приводит к тому, что горизонтально вытянутые объекты фокусируются на разных частях сетчатки, чем вертикально вытянутые объекты, и приводит к искаженным изображениям. [103]
Все эти состояния можно исправить с помощью корректирующих линз . При пресбиопии и гиперметропии собирательная линза обеспечивает дополнительную кривизну, необходимую для приближения ближней точки к глазу, в то время как при миопии рассеивающая линза обеспечивает кривизну, необходимую для удаления дальней точки в бесконечность. Астигматизм исправляется с помощью цилиндрической поверхностной линзы, которая изгибается сильнее в одном направлении, чем в другом, компенсируя неоднородность роговицы. [105]
Оптическая сила корректирующих линз измеряется в диоптриях , величина, обратная фокусному расстоянию, измеренному в метрах; с положительным фокусным расстоянием, соответствующим собирающей линзе, и отрицательным фокусным расстоянием, соответствующим рассеивающей линзе. Для линз, которые также корректируют астигматизм, даются три числа: одно для сферической силы, одно для цилиндрической силы и одно для угла ориентации астигматизма. [105]
Визуальные эффекты

Оптические иллюзии (также называемые зрительными иллюзиями) характеризуются визуально воспринимаемыми изображениями, которые отличаются от объективной реальности. Информация, собранная глазом, обрабатывается в мозге, чтобы дать восприятие , которое отличается от изображаемого объекта. Оптические иллюзии могут быть результатом различных явлений, включая физические эффекты, которые создают изображения, которые отличаются от объектов, которые их создают, физиологические эффекты на глаза и мозг чрезмерной стимуляции (например, яркость, наклон, цвет, движение) и когнитивные иллюзии, когда глаз и мозг делают бессознательные выводы . [106]
Когнитивные иллюзии включают некоторые, которые являются результатом бессознательного неправильного применения определенных оптических принципов. Например, иллюзии комнаты Эймса , Геринга , Мюллера-Лайера , Орбисона , Понцо , Зандера и Вундта, все они основаны на предположении о видимости расстояния с помощью сходящихся и расходящихся линий, таким же образом, как параллельные световые лучи (или, на самом деле, любой набор параллельных линий) кажутся сходящимися в точке схода на бесконечности в двумерных изображениях с художественной перспективой. [107] Это предположение также ответственно за знаменитую лунную иллюзию , когда луна, несмотря на по существу тот же угловой размер, кажется намного больше вблизи горизонта , чем в зените . [ 108] Эта иллюзия настолько сбила с толку Птолемея , что он неправильно приписал ее атмосферной рефракции, когда описал ее в своем трактате «Оптика» . [8]
Другой тип оптической иллюзии использует сломанные узоры, чтобы обмануть разум, заставляя его воспринимать симметрии или асимметрии, которых нет. Примерами служат иллюзии стены кафе , Эренштейна , спирали Фрейзера , Поггендорфа и Целльнера . Связанные, но не строго иллюзии, это узоры, которые возникают из-за наложения периодических структур. Например, прозрачные ткани с сетчатой структурой создают формы, известные как муаровые узоры , в то время как наложение периодических прозрачных узоров, включающих параллельные непрозрачные линии или кривые, создает линейные муаровые узоры. [109]
Оптические приборы

Отдельные линзы имеют множество применений, включая фотографические линзы , корректирующие линзы и увеличительные стекла, в то время как отдельные зеркала используются в параболических отражателях и зеркалах заднего вида . Объединение нескольких зеркал, призм и линз создает составные оптические приборы, которые имеют практическое применение. Например, перископ — это просто два плоских зеркала, выровненных для обеспечения обзора вокруг препятствий. Самыми известными составными оптическими приборами в науке являются микроскоп и телескоп, которые были изобретены голландцами в конце 16 века. [110]
Микроскопы были впервые разработаны всего с двумя линзами: объективом и окуляром . Объектив по сути является увеличительным стеклом и был разработан с очень малым фокусным расстоянием, в то время как окуляр, как правило, имеет большее фокусное расстояние. Это имеет эффект создания увеличенных изображений близких объектов. Как правило, используется дополнительный источник освещения, поскольку увеличенные изображения более тусклые из-за сохранения энергии и распространения световых лучей по большей площади поверхности. Современные микроскопы, известные как составные микроскопы, имеют много линз в них (обычно четыре) для оптимизации функциональности и повышения стабильности изображения. [111] Немного другая разновидность микроскопа, сравнительный микроскоп , смотрит на изображения бок о бок, чтобы создать стереоскопическое бинокулярное изображение, которое кажется трехмерным при использовании человеком. [112]
Первые телескопы, называемые рефракторными телескопами, также были разработаны с одним объективом и окулярной линзой. В отличие от микроскопа, объективная линза телескопа была разработана с большим фокусным расстоянием, чтобы избежать оптических аберраций. Объектив фокусирует изображение удаленного объекта в своей фокусной точке, которая настраивается так, чтобы быть в фокусной точке окуляра с гораздо меньшим фокусным расстоянием. Основная цель телескопа не обязательно заключается в увеличении, а скорее в сборе света, который определяется физическим размером объективной линзы. Таким образом, телескопы обычно обозначаются диаметрами их объективов, а не увеличением, которое можно изменять путем переключения окуляров. Поскольку увеличение телескопа равно фокусному расстоянию объектива, деленному на фокусное расстояние окуляра, окуляры с меньшим фокусным расстоянием дают большее увеличение. [113]
Поскольку изготовление больших линз намного сложнее, чем изготовление больших зеркал, большинство современных телескопов являются рефлекторными телескопами , то есть телескопами, которые используют главное зеркало вместо объектива. К рефлекторным телескопам применимы те же общие оптические соображения, что и к рефракторным телескопам, а именно, чем больше главное зеркало, тем больше света собирается, а увеличение по-прежнему равно фокусному расстоянию главного зеркала, деленному на фокусное расстояние окуляра. Профессиональные телескопы обычно не имеют окуляров, а вместо этого помещают инструмент (часто прибор с зарядовой связью) в фокусную точку. [114]
Фотография


Оптика фотографии включает в себя как линзы, так и среду, в которой регистрируется электромагнитное излучение, будь то пластина , пленка или прибор с зарядовой связью. Фотографы должны учитывать взаимность камеры и снимка, которая суммируется соотношением
- Экспозиция ∝ Площадь диафрагмы × Время экспозиции × Яркость сцены [115]
Другими словами, чем меньше апертура (что обеспечивает большую глубину фокуса), тем меньше света поступает, поэтому продолжительность времени должна быть увеличена (что приводит к возможной размытости, если происходит движение). Примером использования закона взаимности является правило Sunny 16 , которое дает грубую оценку настроек, необходимых для оценки правильной экспозиции при дневном свете. [116]
Диафрагма камеры измеряется безразмерным числом, называемым диафрагменным числом или делением диафрагмы.ж /#, часто обозначается как и задается
где - фокусное расстояние, а - диаметр входного зрачка. По соглашению, "ж /#" рассматривается как один символ, а конкретные значенияж /# записываются путем замены знака числа на значение. Два способа увеличить диафрагму — это либо уменьшить диаметр входного зрачка, либо перейти на большее фокусное расстояние (в случае зум-объектива это можно сделать, просто отрегулировав объектив). Более высокие числа f также имеют большую глубину резкости из -за того, что объектив приближается к пределу камеры-обскуры, которая способна идеально фокусировать все изображения, независимо от расстояния, но требует очень длительного времени экспозиции. [117]
Поле зрения, которое обеспечивает объектив, меняется в зависимости от фокусного расстояния объектива. Существуют три основные классификации, основанные на соотношении диагонального размера пленки или размера сенсора камеры к фокусному расстоянию объектива: [118]
- Нормальный объектив : угол зрения около 50° (называется нормальным , потому что этот угол считается примерно эквивалентным человеческому зрению [118] ) и фокусное расстояние примерно равно диагонали пленки или сенсора. [119]
- Широкоугольный объектив : угол обзора шире 60°, а фокусное расстояние короче, чем у обычного объектива. [120]
- Длиннофокусный объектив : угол обзора уже, чем у обычного объектива. Это любой объектив с фокусным расстоянием больше, чем диагональ пленки или сенсора. [121] Наиболее распространенным типом длиннофокусного объектива является телеобъектив , конструкция которого использует специальную телефотогруппу , чтобы быть физически короче своего фокусного расстояния. [122]
Современные зум-объективы могут обладать некоторыми или всеми этими характеристиками.
Абсолютное значение требуемого времени экспозиции зависит от того, насколько чувствителен к свету используемый носитель (измеряется светочувствительностью пленки или, для цифровых носителей, квантовой эффективностью ). [123] Ранняя фотография использовала носители с очень низкой светочувствительностью, поэтому время экспозиции должно было быть большим даже для очень ярких снимков. По мере совершенствования технологий улучшалась и чувствительность пленочных и цифровых камер. [124]
Другие результаты физической и геометрической оптики применимы к оптике камеры. Например, максимальная разрешающая способность конкретной настройки камеры определяется пределом дифракции , связанным с размером зрачка и заданным, грубо говоря, критерием Рэлея. [125]
Атмосферная оптика

Уникальные оптические свойства атмосферы вызывают широкий спектр захватывающих оптических явлений. Голубой цвет неба является прямым результатом рэлеевского рассеяния, которое перенаправляет более высокочастотный (синий) солнечный свет обратно в поле зрения наблюдателя. Поскольку синий свет рассеивается легче, чем красный, солнце приобретает красноватый оттенок, когда оно наблюдается через толстую атмосферу, как во время восхода или заката . Дополнительные твердые частицы в небе могут рассеивать разные цвета под разными углами, создавая красочные светящиеся небеса в сумерках и на рассвете. Рассеивание ледяных кристаллов и других частиц в атмосфере ответственно за гало , послесвечения , короны , лучи солнечного света и ложные солнца . Различия в этих видах явлений обусловлены различными размерами и геометрией частиц. [126]
Миражи — это оптические явления, при которых лучи света изгибаются из-за температурных изменений показателя преломления воздуха, создавая смещенные или сильно искаженные изображения удаленных объектов. Другие драматические оптические явления, связанные с этим, включают эффект Новой Земли , когда солнце кажется встающим раньше, чем предполагалось, и имеет искаженную форму. Эффектная форма рефракции происходит с температурной инверсией, называемой Фата-Моргана , когда объекты на горизонте или даже за горизонтом, такие как острова, скалы, корабли или айсберги, кажутся удлиненными и приподнятыми, как «сказочные замки». [127]
Радуги являются результатом сочетания внутреннего отражения и дисперсионной рефракции света в каплях дождя. Однократное отражение от задней части массива капель дождя создает радугу с угловым размером на небе, который варьируется от 40° до 42° с красным цветом снаружи. Двойные радуги создаются двумя внутренними отражениями с угловым размером от 50,5° до 54° с фиолетовым цветом снаружи. Поскольку радуги видны, когда солнце находится на расстоянии 180° от центра радуги, радуги тем заметнее, чем ближе солнце к горизонту. [128]
Смотрите также
Ссылки
- ^ ab McGraw-Hill Encyclopedia of Science and Technology (5-е изд.). McGraw-Hill. 1993.
- ^ "Самый старый телескоп в мире?". BBC News . 1 июля 1999 г. Архивировано из оригинала 1 февраля 2009 г. Получено 3 января 2010 г.
- ^ TF Hoad (1996). Краткий Оксфордский словарь английской этимологии. ISBN 978-0-19-283098-2.
- ^ История глаза. Архивировано 20 января 2012 г. на Wayback Machine . stanford.edu. Получено 10 июня 2012 г.
- ^ TL Heath (2003). Учебник греческой математики . Courier Dover Publications. С. 181–182. ISBN 978-0-486-43231-1.
- ^ Уильям Р. Уттал (1983). Визуальное обнаружение формы в трехмерном пространстве. Psychology Press. стр. 25–. ISBN 978-0-89859-289-4. Архивировано из оригинала 2016-05-03.
- ^ Евклид (1999). Элахе Хейрандиш (ред.). Арабская версия оптики Евклида = Китаб Уклидис фи ихтилаф аль-манацир . Нью-Йорк: Спрингер. ISBN 978-0-387-98523-7.
- ^ ab Ptolemy (1996). А. Марк Смит (ред.). Теория зрительного восприятия Птолемея: английский перевод Оптики с введением и комментариями . DIANE Publishing. ISBN 978-0-87169-862-9.
- ^ Адамсон, Питер (2006). «Аль-Кинди и восприятие греческой философии». В Адамсон, Питер; Тейлор, Р.. Кембриджский компаньон арабской философии. Cambridge University Press. стр. 45. ISBN 978-0-521-52069-0 .
- ^ ab Rashed, Roshdi (1990). «Пионер в анакластике: Ибн Сахл о сжигании зеркал и линз». Isis . 81 (3): 464–491. doi :10.1086/355456. JSTOR 233423. S2CID 144361526.
- ^
- Хогендейк, Ян П.; Сабра, Абдельхамид И., ред. (2003). Предприятие науки в исламе: новые перспективы . MIT Press. стр. 85–118. ISBN 978-0-262-19482-2. OCLC 50252039.
- G. Hatfield (1996). «Была ли научная революция действительно революцией в науке?». В FJ Ragep; P. Sally; SJ Livesey (ред.). Традиция, передача, трансформация: Труды двух конференций по досовременной науке, проведенных в Университете Оклахомы. Brill Publishers. стр. 500. ISBN 978-90-04-10119-7. Архивировано из оригинала 2016-04-27.
- Надер Эль-Бизри (2005). «Философская перспектива оптики Альхазена». Арабские науки и философия . 15 (2): 189–218. doi :10.1017/S0957423905000172. S2CID 123057532.
- Надер Эль-Бизри (2007). «В защиту суверенитета философии: критика аль-Багдади геометризации места Ибн аль-Хайтама». Арабские науки и философия . 17 : 57–80. doi :10.1017/S0957423907000367. S2CID 170960993.
- G. Simon (2006). «Взгляд у Ибн аль-Хайтама». The Medieval History Journal . 9 : 89–98. doi :10.1177/097194580500900105. S2CID 170628785.
- ^ Ян П. Ховард; Брайан Дж. Роджерс (1995). Бинокулярное зрение и стереопсис. Oxford University Press. стр. 7. ISBN 978-0-19-508476-4. Архивировано из оригинала 2016-05-06.
- ^ Елена Агацци; Энрико Джаннетто; Франко Джудиче (2010). Представление света в искусстве и науке: теории и практики. V&R unipress GmbH. стр. 42. ISBN 978-3-89971-735-8. Архивировано из оригинала 2016-05-10.
- ^ Эль-Бизри, Надер (2010). «Классическая оптика и традиции перспективы, ведущие к Ренессансу». В Хендрикс, Джон Шеннон ; Карман, Чарльз Х. (ред.). Ренессансные теории зрения (визуальная культура в раннем модернизме) . Фарнем, Суррей: Ashgate Publishing . стр. 11–30. ISBN 978-1-4094-0024-0.; Эль-Бизри, Надер (2014). «Видение реальности в перспективе: «Искусство оптики» и «Наука живописи»". В Lupacchini, Rossella; Angelini, Annarita (ред.). Искусство науки: от перспективного рисунка до квантовой случайности . Doredrecht: Springer. стр. 25–47.
- ^ DC Lindberg, Теории зрения от аль-Кинди до Кеплера , (Чикаго: Univ. of Chicago Pr., 1976), стр. 94–99.
- ^ Иларди, Винсент (2007). Ренессансное видение от очков до телескопов. Филадельфия: Американское философское общество. С. 4–5. ISBN 978-0-87169-259-7.
- ^ «Проект Галилео > Наука > Телескоп» Эла Ван Хелдена. Архивировано 20 марта 2012 г. на Wayback Machine . Galileo.rice.edu. Получено 10 июня 2012 г.
- ^ Генри К. Кинг (2003). История телескопа. Courier Dover Publications. стр. 27. ISBN 978-0-486-43265-6. Архивировано из оригинала 2016-06-17.
- ^ Пол С. Агуттер; Денис Н. Уитли (2008). Размышления о жизни: история и философия биологии и других наук. Springer. стр. 17. ISBN 978-1-4020-8865-0. Архивировано из оригинала 2016-05-16.
- ^ Иларди (2007), стр. 210.
- ^ Микроскопы: Хронология Архивировано 2010-01-09 в Wayback Machine , Nobel Foundation. Получено 3 апреля 2009 г.
- ^ Уотсон, Фред (2007). Звездочет: Жизнь и времена телескопа. Аллен и Анвин. стр. 55. ISBN 978-1-74175-383-7. Архивировано из оригинала 2016-05-08.
- ^ Каспар, Макс (1993) [Впервые опубликовано в 1959]. Kepler . Dover Publications. стр. 142–146. ISBN 0-486-67605-6.
- ^ Иларди (2007), стр. 244.
- ^ Каспар (1993), стр. 192–202.
- ^ ab AI Sabra (1981). Теории света от Декарта до Ньютона . Архив CUP. ISBN 978-0-521-28436-3.
- ^ WF Magie (1935). Справочник по физике. Издательство Гарвардского университета. С. 309.
- ^ Дж. К. Максвелл (1865). "Динамическая теория электромагнитного поля" . Philosophical Transactions of the Royal Society of London . 155 : 459–512. Bibcode : 1865RSPT..155..459M. doi : 10.1098/rstl.1865.0008. S2CID 186207827.
- ^ Для обоснованного подхода к сложности интеллектуальных мотивов Планка в отношении кванта, для его неохотного принятия его последствий, см. H. Kragh, Max Planck: the reluctant revolution (Макс Планк: неохотный революционер). Архивировано 01.04.2012 в Wayback Machine , Physics World . Декабрь 2000 г.
- ^ Эйнштейн, А. (1967). «Об эвристической точке зрения относительно производства и преобразования света». В Ter Haar, D. (ред.). The Old Quantum Theory . Pergamon. стр. 91–107. OCLC 534625.Глава представляет собой английский перевод статьи Эйнштейна 1905 года о фотоэлектрическом эффекте.
- ^ Эйнштейн, А. (1905). «Über einen die Erzeugung und Verwandlung des Lichtes betreffenden heuristischen Gesichtspunkt» [Об эвристической точке зрения на производство и преобразование света]. Аннален дер Физик (на немецком языке). 322 (6): 132–148. Бибкод : 1905АнП...322..132Е. дои : 10.1002/andp.19053220607 .
- ^ «О строении атомов и молекул». Philosophical Magazine . 26, Series 6: 1–25. 1913. Архивировано из оригинала 4 июля 2007 года.. Историческая работа, положившая начало боровской модели атома и молекулярной связи .
- ^ Р. Фейнман (1985). "Глава 1". QED: Странная теория света и материи . Princeton University Press. стр. 6. ISBN 978-0-691-08388-9.
- ^ Н. Тейлор (2000). ЛАЗЕР: Изобретатель, лауреат Нобелевской премии и тридцатилетняя патентная война . Нью-Йорк: Simon & Schuster. ISBN 978-0-684-83515-0.
- ^ Ариэль Липсон; Стивен Г. Липсон; Генри Липсон (28 октября 2010 г.). Оптическая физика. Cambridge University Press. стр. 48. ISBN 978-0-521-49345-1. Архивировано из оригинала 28 мая 2013 . Получено 12 июля 2012 .
- ^ Артур Шустер (1904). Введение в теорию оптики. Э. Арнольд. стр. 41.
- ^ JE Greivenkamp (2004). Полевое руководство по геометрической оптике. SPIE Field Guides vol. FG01. SPIE. стр. 19–20. ISBN 978-0-8194-5294-8.
- ^ ab Young & Freedman (2020), стр. 1109.
- ↑ Янг и Фридман (2020), стр. 1112–1113.
- ↑ Янг и Фридман (2020), стр. 1142–1143, 1145.
- ^ ab Young & Freedman (2020), стр. 1116.
- ^ Маршанд, Э. У. (1978). Оптика градиентного индекса . Нью-Йорк: Academic Press.
- ↑ Янг и Фридман (2020), стр. 1113–1115.
- ^ Хехт (2017), стр. 159.
- ^ Хехт (2017), стр. 165.
- ^ Янг и Фридман (2020), стр. 1157.
- ^ Янг и Фридман (2020), стр. 1143,1163,1175.
- ^ М. В. Кляйн и Т. Е. Фуртак, 1986, Оптика, John Wiley & Sons, Нью-Йорк ISBN 0-471-87297-0 .
- ^ Максвелл, Джеймс Клерк (1865). "Динамическая теория электромагнитного поля" (PDF) . Philosophical Transactions of the Royal Society of London . 155 : 499. Bibcode :1865RSPT..155..459M. doi :10.1098/rstl.1865.0008. S2CID 186207827. Архивировано (PDF) из оригинала 28.07.2011.Эта статья сопровождала выступление Максвелла перед Королевским обществом 8 декабря 1864 года. См. также Динамическая теория электромагнитного поля .
- ^ М. Борн и Э. Вольф (1999). Принцип оптики . Кембридж: Издательство Кембриджского университета. ISBN 0-521-64222-1 .
- ^ Дж. Гудман (2005). Введение в Фурье-оптику (3-е изд.). Roberts & Co Publishers. ISBN 978-0-9747077-2-3.
- ^ А. Э. Зигман (1986). Лазеры . Университетские научные книги. ISBN 978-0-935702-11-8.Глава 16.
- ↑ Янг и Фридман (2020), стр. 1187–1188.
- ^ Янг и Фридман (2020), стр. 512, 1189.
- ↑ Янг и Фридман (2020), стр. 1191–1192.
- ^ ab P. Hariharan (2003). Оптическая интерферометрия (PDF) (2-е изд.). Сан-Диего, США: Academic Press. ISBN 978-0-12-325220-3. Архивировано (PDF) из оригинала 2008-04-06.
- ^ ER Hoover (1977). Колыбель величия: национальные и мировые достижения Западного резерва Огайо . Кливленд: Shaker Savings Association.
- ↑ Янг и Фридман (2020), стр. 1198–1200.
- ^ Обер, JL (1760). Memoires pour l'histoire des Sciences et des beaux arts [ Мемуары по истории науки и изящных искусств ] (на французском языке). Париж: Отпечаток. де САС; Чез Э. Гано. п. 149.
- ^ Брюстер, Д. (1831). Трактат по оптике. Лондон: Longman, Rees, Orme, Brown & Green и John Taylor. стр. 95.
- ^ Гук, Р. (1665). Micrographia: или, Некоторые физиологические описания мельчайших тел, сделанные с помощью увеличительных стекол. Лондон: J. Martyn и J. Allestry. ISBN 978-0-486-49564-4.
- ^ Тернбулл, HW (1940–1941). «Ранние шотландские отношения с Королевским обществом: I. Джеймс Грегори, FRS (1638–1675)». Заметки и записи Лондонского королевского общества . 3 : 22–38. doi : 10.1098/rsnr.1940.0003 .
- ^ Ротман, Т. (2003). Все относительно и другие басни в науке и технике . Нью-Джерси: Wiley. ISBN 978-0-471-20257-8.
- ^ Хехт (2017), стр. 5.
- ^ Хехт (2017), стр. 398–399; Янг и Фридман (2020), стр. 1192.
- ^ Хехт (2017), стр. 488–491; Янг и Фридман (2020), стр. 1224–1225.
- ^ Лонгхерст, Р. С. (1968). Геометрическая и физическая оптика (2-е изд.). Лондон: Longmans. Bibcode :1967gpo..book.....L.
- ^ Хехт (2017), стр. 497; Янг и Фридман (2020), стр. 1228–1230.
- ^ Хехт (2017), стр. 482.
- ^ Хехт (2017), стр. 485; Янг и Фридман (2020), стр. 1232.
- ^ Таббс, Роберт Найджел (сентябрь 2003 г.). Удачные экспозиции: дифракционно-ограниченные астрономические изображения в атмосфере (диссертация). Кембриджский университет. Архивировано из оригинала 2008-10-05.
- ^ CF Bohren & DR Huffman (1983). Поглощение и рассеяние света малыми частицами . Wiley. ISBN 978-0-471-29340-8.
- ^ ab JD Jackson (1975). Классическая электродинамика (2-е изд.). Wiley. стр. 286. ISBN 978-0-471-43132-9.
- ^ Хехт (2017), стр. 202–204.
- ^ ab R. Ramaswami; KN Sivarajan (1998). Оптические сети: практическая перспектива. Лондон: Academic Press. ISBN 978-0-12-374092-2. Архивировано из оригинала 2015-10-27.
- ^ Бриллюэн, Леон. Распространение волн и групповая скорость . Academic Press Inc., Нью-Йорк (1960)
- ^ M. Born & E. Wolf (1999). Принцип оптики . Кембридж: Cambridge University Press. С. 14–24. ISBN 978-0-521-64222-4.
- ^ Хехт (2017), стр. 333–334; Янг и Фридман (2020), стр. 1083, 1118.
- ^ ab Hecht (2017), стр. 336.
- ^ Хехт (2017), стр. 330–332; Янг и Фридман (2020), стр. 1123.
- ^ Хехт (2017), стр. 333–334; Янг и Фридман (2020), стр. 1123.
- ^ Хехт (2017), стр. 334–335; Янг и Фридман (2020), стр. 1124.
- ^ Хехт (2017), стр. 379–383.
- ^ Янг и Фридман (2020), стр. 1124.
- ^ Хехт (2017), стр. 367, 373.
- ^ Хехт (2017), стр. 372; Янг и Фридман (2020), стр. 1124–1125.
- ^ FJ Duarte (2015). Tunable Laser Optics (2-е изд.). Нью-Йорк: CRC. С. 117–120. ISBN 978-1-4822-4529-5. Архивировано из оригинала 2015-04-02.
- ^ Хехт (2017), стр. 338; Янг и Фридман (2020), стр. 1119–1121.
- ^ Хехт (2017), стр. 339–342.
- ^ Хехт (2017), стр. 355–358.
- ^ Хехт (2017), стр. 353–356.
- ^ Уоллс, Дэниел Франк ; Милберн, Г. Дж. (1994). Квантовая оптика . Springer.
- ^ МакОлей, Аластер Д. (16 января 1991 г.). Архитектура оптических компьютеров: применение оптических концепций к компьютерам следующего поколения . Wiley. ISBN 978-0-471-63242-9.
- ^ Шен, YR (1984). Принципы нелинейной оптики . Нью-Йорк: Wiley-Interscience. ISBN 978-0-471-88998-4.
- ^ "laser". Reference.com. Архивировано из оригинала 2008-03-31 . Получено 2008-05-15 .
- ^ Чарльз Х. Таунс – Нобелевская лекция. Архивировано 11 октября 2008 г. на Wayback Machine . nobelprize.org
- ^ "Искусственная звезда VLT". ESO Picture of the Week . Архивировано из оригинала 3 июля 2014 года . Получено 25 июня 2014 года .
- ^ CH Townes. "Первый лазер". Чикагский университет. Архивировано из оригинала 2008-05-17 . Получено 2008-05-15 .
- ^ CH Townes (2003). «Первый лазер». В Лоре Гарвин ; Тим Линкольн (ред.). Век природы: двадцать одно открытие, изменившее науку и мир. Издательство Чикагского университета. С. 107–112. ISBN 978-0-226-28413-2.
- ^ Что такое штрих-код? Архивировано 23.04.2012 на Wayback Machine denso-wave.com
- ^ "Как был разработан CD". BBC News . 2007-08-17. Архивировано из оригинала 2012-01-07 . Получено 2007-08-17 .
- ^ J. Wilson & JFB Hawkes (1987). Лазеры: принципы и применение, Prentice Hall International Series in Optoelectronics . Prentice Hall. ISBN 978-0-13-523697-0.
- ^ abc D. Atchison & G. Smith (2000). Оптика человеческого глаза . Elsevier. ISBN 978-0-7506-3775-6.
- ^ аб Э. Р. Кандель; Дж. Х. Шварц; ТМ Джесселл (2000). Принципы нейронауки (4-е изд.). Нью-Йорк: МакГроу-Хилл. стр. 507–513. ISBN 978-0-8385-7701-1.
- ^ ab D. Meister. "Ophthalmic Lens Design". OptiCampus.com. Архивировано из оригинала 27 декабря 2008 г. Получено 12 ноября 2008 г.
- ^ J. Bryner (2008-06-02). "Ключ ко всем оптическим иллюзиям открыт". LiveScience. Архивировано из оригинала 2008-09-05.
- ^ Геометрия точки схода Архивировано 22.06.2008 на Wayback Machine в Convergence Архивировано 13.07.2007 на Wayback Machine
- ^ "The Moon Illusion Explained" Архивировано 04.12.2015 в Wayback Machine , Дон Маккриди, Университет Висконсин-Уайтуотер
- ^ AK Jain; M. Figueiredo; J. Zerubia (2001). Методы минимизации энергии в компьютерном зрении и распознавании образов. Springer. ISBN 978-3-540-42523-6.
- ↑ Янг и Фридман (2020), стр. 1171–1175.
- ↑ Янг и Фридман (2020), стр. 1171–1173.
- ^ PE Nothnagle; W. Chambers; MW Davidson. «Введение в стереомикроскопию». Nikon MicroscopyU. Архивировано из оригинала 2011-09-16.
- ^ Янг и Фридман (2020), стр. 1174.
- ^ Янг и Фридман (2020), стр. 1175.
- ^ Сэмюэл Эдвард Шеппард и Чарльз Эдвард Кеннет Мис (1907). Исследования по теории фотографического процесса. Longmans, Green and Co. стр. 214.
- ^ BJ Suess (2003). Мастерство черно-белой фотографии. Allworth Communications. ISBN 978-1-58115-306-4.
- ^ MJ Langford (2000). Базовая фотография. Focal Press. ISBN 978-0-240-51592-2.
- ^ ab Warren, Bruce (2001). Фотография. Cengage Learning. стр. 71. ISBN 978-0-7668-1777-7. Архивировано из оригинала 2016-08-19.
- ^ Лесли Д. Штробель (1999). Посмотреть технику камеры. Фокальная пресса. ISBN 978-0-240-80345-6.
- ^ S. Simmons (1992). Использование камеры View . Amphoto Books. стр. 35. ISBN 978-0-8174-6353-3.
- ^ Сидни Ф. Рэй (2002). Прикладная фотографическая оптика: объективы и оптические системы для фотографии, кино, видео, электронных и цифровых изображений. Focal Press. стр. 294. ISBN 978-0-240-51540-3. Архивировано из оригинала 2016-08-19.
- ^ New York Times Staff (2004). The New York Times Guide to Essential Knowledge. Macmillan. ISBN 978-0-312-31367-8.
- ^ RR Carlton; A. McKenna Adler (2000). Принципы рентгенографической визуализации: искусство и наука. Thomson Delmar Learning. ISBN 978-0-7668-1300-7.
- ^ W. Crawford (1979). Хранители света: история и рабочее руководство по ранним фотографическим процессам . Dobbs Ferry, NY: Morgan & Morgan. стр. 20. ISBN 978-0-87100-158-0.
- ^ JM Cowley (1975). Физика дифракции . Амстердам: Северная Голландия. ISBN 978-0-444-10791-6.
- ^ CD Ahrens (1994). Метеорология сегодня: введение в погоду, климат и окружающую среду (5-е изд.). West Publishing Company. стр. 88–89. ISBN 978-0-314-02779-5.
- ^ А. Янг. "Введение в миражи". Архивировано из оригинала 2010-01-10.
- ↑ Янг и Фридман (2020), стр. 1117–1118.
Цитируемые работы
- Хехт, Юджин (2017). Оптика (5-е изд.). Pearson Education. ISBN 978-0-133-97722-6.
- Янг, Хью Д.; Фридман, Роджер А. (2020). Университетская физика: расширенная версия с современной физикой (15-е изд.). Pearson Education. ISBN 978-1-292-31473-0.
Дальнейшее чтение
- Борн, Макс; Вольф, Эмиль (2002). Принципы оптики . Cambridge University Press. ISBN 978-1-139-64340-5.
- Фаулз, Грант Р. (1975). Введение в современную оптику (4-е изд.). Эддисон-Уэсли Лонгман.
- Липсон, Стивен Г.; Липсон, Генри; Тангейзер, Дэвид Стефан (1995). Оптическая физика . Издательство Кембриджского университета. ISBN 978-0-521-43631-1.
- Serway, Raymond A.; Jewett, John W. (2004). Physics for Scientists and Engineers (6-е, иллюстрированное издание). Belmont, California: Thomson-Brooks/Cole. ISBN 978-0-534-40842-8.
- Типлер, Пол А.; Моска, Джин (2004). Физика для ученых и инженеров: электричество, магнетизм, свет и элементарная современная физика . Том 2. WH Freeman. ISBN 978-0-7167-0810-0.
Внешние ссылки
- Соответствующие обсуждения
- Оптика в программе «В наше время » на BBC
- Учебники и учебные пособия
- Свет и материя – учебник с открытым исходным кодом, содержащий изучение оптики в главах 28–32.
- Optics2001 – Библиотека и сообщество по оптике
- Фундаментальная оптика – Техническое руководство Меллеса Гриота
- Физика света и оптика – Книга для бакалавров Университета имени Бригама Янга
- Оптика для фотоэлектрических систем – пошаговое введение в классическую оптику
- Дальнейшее чтение
- Оптика и фотоника: физика, улучшающая нашу жизнь. Публикации Института физики
- Общества
|
|























