преобразование Энскомба

В статистике преобразование Анскомба , названное в честь Фрэнсиса Анскомба , представляет собой стабилизирующее дисперсию преобразование , которое преобразует случайную величину с распределением Пуассона в величину с приблизительно стандартным гауссовым распределением . Преобразование Анскомба широко используется в ограниченных фотонами изображениях (астрономия, рентген), где изображения естественным образом следуют закону Пуассона. Преобразование Анскомба обычно используется для предварительной обработки данных, чтобы сделать стандартное отклонение приблизительно постоянным. Затем используются алгоритмы шумоподавления, разработанные для структуры аддитивного белого гауссовского шума ; окончательная оценка затем получается путем применения обратного преобразования Анскомба к очищенным от шумов данным.

Для распределения Пуассона среднее значение и дисперсия не являются независимыми: Преобразование Анскомба ^[1]${\displaystyle м}$${\displaystyle v}$${\displaystyle m=v}$

${\displaystyle A:x\mapsto 2{\sqrt {x+{\tfrac {3}{8}}}}\,}$

направлен на преобразование данных таким образом, чтобы дисперсия была установлена ​​приблизительно равной 1 для достаточно большого среднего значения; при нулевом среднем значении дисперсия по-прежнему равна нулю.

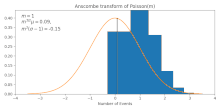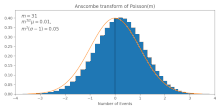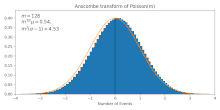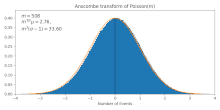
Он преобразует пуассоновские данные (со средним значением ) в приблизительно гауссовские данные со средним значением и стандартным отклонением . Это приближение становится более точным для больших , ^[2] как также можно увидеть на рисунке.${\displaystyle x}$${\displaystyle м}$${\displaystyle 2{\sqrt {m+{\tfrac {3}{8}}}}-{\tfrac {1}{4\,m^{1/2}}}+O\left({\tfrac {1}{m^{3/2}}}\right)}$${\displaystyle 1+O\left({\tfrac {1}{m^{2}}}\right)}$${\displaystyle m}$

Для преобразованной переменной вида выражение для дисперсии имеет дополнительный член ; он сводится к нулю при , что и является причиной выбора этого значения.${\displaystyle 2{\sqrt {x+c}}}$${\displaystyle {\frac {{\tfrac {3}{8}}-c}{m}}}$${\displaystyle c={\tfrac {3}{8}}}$

Когда преобразование Анскомба используется для шумоподавления (т.е. когда цель состоит в том, чтобы получить из оценки ), его обратное преобразование также необходимо для того, чтобы вернуть стабилизированные по дисперсии и шумоподавленные данные в исходный диапазон. Применение алгебраического обратного${\displaystyle x}$${\displaystyle m}$${\displaystyle y}$

${\displaystyle A^{-1}:y\mapsto \left({\frac {y}{2}}\right)^{2}-{\frac {3}{8}}}$

обычно вносит нежелательное смещение в оценку среднего значения , поскольку прямое квадратно-корневое преобразование не является линейным . Иногда используют асимптотически несмещенное обратное ^[1]${\displaystyle m}$

${\displaystyle y\mapsto \left({\frac {y}{2}}\right)^{2}-{\frac {1}{8}}}$

смягчает проблему смещения, но это не относится к изображениям, ограниченным фотонами, для которых точное несмещенное обратное значение задается неявным отображением ^[3]

${\displaystyle \operatorname {E} \left[2{\sqrt {x+{\tfrac {3}{8}}}}\mid m\right]=2\sum _{x=0}^{+\infty }\left({\sqrt {x+{\tfrac {3}{8}}}}\cdot {\frac {m^{x}e^{-m}}{x!}}\right)\mapsto m}$

следует использовать. Замкнутая форма приближения этой точной несмещенной обратной величины ^[4]

${\displaystyle y\mapsto {\frac {1}{4}}y^{2}-{\frac {1}{8}}+{\frac {1}{4}}{\sqrt {\frac {3}{2}}}y^{-1}-{\frac {11}{8}}y^{-2}+{\frac {5}{8}}{\sqrt {\frac {3}{2}}}y^{-3}.}$

Существует много других возможных преобразований, стабилизирующих дисперсию для распределения Пуассона. Бар-Лев и Энис сообщают ^[2] о семействе таких преобразований, которое включает преобразование Анскомба. Другим членом семейства является преобразование Фримена-Тьюки ^[5]

${\displaystyle A:x\mapsto {\sqrt {x+1}}+{\sqrt {x}}.\,}$

Упрощенное преобразование, полученное как примитив обратной величины стандартного отклонения данных , имеет вид

${\displaystyle A:x\mapsto 2{\sqrt {x}}\,}$

который, хотя и не так хорош в стабилизации дисперсии, имеет преимущество в том, что его легче понять. Действительно, из метода дельта ,

${\displaystyle V[2{\sqrt {x}}]\approx \left({\frac {d(2{\sqrt {m}})}{dm}}\right)^{2}V[x]=\left({\frac {1}{\sqrt {m}}}\right)^{2}m=1}$.

Хотя преобразование Анскомба подходит для чистых данных Пуассона, во многих приложениях данные также представляют собой аддитивную гауссовскую компоненту. Эти случаи обрабатываются обобщенным преобразованием Анскомба ^[6] и его асимптотически несмещенными или точными несмещенными обратными. ^[7]

• Преобразование, стабилизирующее дисперсию
• Преобразование Бокса–Кокса

• Старк, Дж.-Л.; Муртаг, Ф. (2001), «Астрономические изображения и обработка сигналов: взгляд на шум, информацию и масштаб», журнал Signal Processing Magazine, IEEE , т. 18, № 2, стр. 30–40, Bibcode : 2001ISPM...18...30S, doi : 10.1109/79.916319, S2CID  13210703