3
Эта статья включает список общих ссылок , но в ней отсутствуют соответствующие встроенные цитаты . ( Февраль 2024 ) |
| ||||
|---|---|---|---|---|
| Кардинал | три | |||
| Порядковый | 3-й (третий) | |||
| Система счисления | троичный | |||
| Факторизация | основной | |||
| Основной | 2-й | |||
| Делители | 1, 3 | |||
| греческое число | Г´ | |||
| римская цифра | III, iii | |||
| греческий префикс | три- | |||
| латинский префикс | тре-/тер- | |||
| Двоичный | 11 2 | |||
| Тройной | 10 3 | |||
| Шестизначный | 3 6 | |||
| Восьмеричный | 3 8 | |||
| Двенадцатеричная система счисления | 3 12 | |||
| Шестнадцатеричный | 3 16 | |||
| Арабский , курдский , персидский , синдхи , урду | 3 | |||
| бенгальский , ассамский | ৩ | |||
| китайский | Да, хорошо, хорошо | |||
| Деванагари | ३ | |||
| Геэз | ፫ | |||
| греческий | γ (или Γ) | |||
| иврит | ג | |||
| японский | 三/参 | |||
| кхмерский | ៣ | |||
| армянский | Գ | |||
| малаялам | ൩ | |||
| тамильский | ௩ | |||
| телугу | ౩ | |||
| каннада | ೩ | |||
| тайский | ๓ | |||
| Н'Ко | � | |||
| Лаосский | ໓ | |||
| грузинский | Ⴂ/ⴂ/გ ( Гани ) | |||
| Вавилонское число | 𒐗 | |||
| Цифры майя | ••• | |||
| азбука Морзе | ... _ _ | |||
3 ( три ) — число , цифра и число . Это натуральное число , следующее за 2 и предшествующее 4 , и является наименьшим нечетным простым числом и единственным простым числом, предшествующим квадратному числу. Оно имеет религиозное и культурное значение во многих обществах.
Эволюция арабской цифры
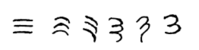
Использование трех линий для обозначения числа 3 встречалось во многих системах письма, включая некоторые (например, римские и китайские цифры ), которые все еще используются. Это было также первоначальное представление числа 3 в брахмической (индийской) числовой нотации, ее самые ранние формы были выровнены по вертикали. [1] Однако во времена империи Гупта знак был изменен путем добавления кривой на каждой строке. Письмо нагари вращало линии по часовой стрелке, поэтому они отображались горизонтально, и заканчивало каждую строку коротким нисходящим штрихом справа. В курсивном письме три штриха в конечном итоге были соединены, образуя глиф, напоминающий ⟨3⟩ с дополнительным штрихом внизу: ३ .
Индийские цифры распространились в Халифате в IX веке. Нижний штрих был убран около X века в западных частях Халифата, таких как Магриб и Аль -Андалус , когда развился особый вариант («западноарабский») цифровых символов, включая современную западную 3. Напротив, восточные арабы сохранили и увеличили этот штрих, повернув цифру еще раз, чтобы получить современную («восточную») арабскую цифру « ٣ ». [2]
В большинстве современных западных шрифтов цифра 3, как и другие десятичные цифры , имеет высоту заглавной буквы и располагается на базовой линии . В шрифтах с текстовыми цифрами , с другой стороны, глиф обычно имеет высоту строчной буквы "x" и выносного элемента : " ". Однако в некоторых французских текстово-цифровых шрифтах вместо подстрочного элемента используется выносной элемент .
". Однако в некоторых французских текстово-цифровых шрифтах вместо подстрочного элемента используется выносной элемент .
Распространенный графический вариант цифры три имеет плоскую вершину, похожую на букву Ʒ (ezh). Эта форма иногда используется для предотвращения фальсификации цифры 3 как 8. Она встречается в штрих-кодах UPC-A и стандартных колодах из 52 карт .
Математика
По мнению Пифагора и пифагорейской школы, число 3, которое они называли триадой , является единственным числом, равным сумме всех членов, находящихся ниже него, и единственным числом, сумма которого с членами, находящимися ниже, равна их произведению на себя. [3]
Правило делимости
Натуральное число делится на три, если сумма его цифр в десятичной системе счисления делится на 3. Например, число 21 делится на три (3 раза по 7), а сумма его цифр равна 2 + 1 = 3. Из-за этого обратное число любого числа, делящегося на три (или, конечно, любая перестановка его цифр), также делится на три. Например, 1368 и его обратное число 8631 оба делятся на три (как и 1386, 3168, 3186, 3618 и т. д.). См. также Правило делимости . Это работает в десятичной системе счисления и в любой позиционной системе счисления , основание которой делится на три, оставляя остаток один (основания 4, 7, 10 и т. д.).
Свойства числа
3 — второе наименьшее простое число и первое нечетное простое число. Это первое уникальное простое число , такое, что значение длины периода 1 десятичного разложения его обратной величины , 0,333..., уникально. 3 — простое число-близнец с 5 и двоюродное простое число с 7 , и единственное известное число, такое что ! − 1 и ! + 1 являются простыми, а также единственное простое число, такое что − 1 дает другое простое число, 2. Треугольник состоит из трех сторон . Это наименьший несамопересекающийся многоугольник и единственный многоугольник , не имеющий собственных диагоналей . При выполнении быстрых оценок 3 является грубым приближением π , 3,1415..., и очень грубым приближением e , 2,71828...
3 является первым простым числом Мерсенна , а также вторым показателем простого числа Мерсенна и вторым показателем двойного простого числа Мерсенна для 7 и 127 соответственно. 3 также является первым из пяти известных простых чисел Ферма , которые включают 5, 17 , 257 и 65537. Это второе простое число Фибоначчи (и второе простое число Люка ), второе простое число Софи Жермен , третье число Харшада в десятичной системе счисления и второе простое факториал , поскольку оно равно 2! + 1.
3 — второе и единственное простое треугольное число , и Гаусс доказал, что каждое целое число является суммой не более 3 треугольных чисел .
Три — единственное простое число, которое на единицу меньше полного квадрата . Любое другое число, которое равно − 1 для некоторого целого числа, не является простым, так как оно равно ( − 1)( + 1). Это верно и для 3 (с = 2), но в этом случае меньший множитель равен 1. Если больше 2, то и − 1, и + 1 больше 1, поэтому их произведение не является простым.
Связанные свойства
Трисекция угла была одной из трех знаменитых задач древности.
3 — количество неколлинеарных точек, необходимое для определения плоскости , окружности и параболы .
Существует только три различных панмагических квадрата 4×4 .
Три из пяти Платоновых тел имеют треугольные грани – тетраэдр , октаэдр и икосаэдр . Кроме того, три из пяти Платоновых тел имеют вершины , где встречаются три грани – тетраэдр , гексаэдр ( куб ) и додекаэдр . Кроме того, только три различных типа многоугольников составляют грани пяти Платоновых тел – треугольник , квадрат и пентагон .
Существуют три конечные выпуклые однородные группы многогранников в трех измерениях, помимо бесконечных семейств призм и антипризм : тетраэдральная группа , октаэдральная группа и икосаэдральная группа . В размерностях ⩾ 5 существуют только три правильных многогранника: -симплексы , -кубы и -ортоплексы . В размерностях ⩾ 9 единственными тремя однородными семействами многогранников, помимо многочисленных бесконечных пропризматических семейств, являются симплексные , кубические и полугиперкубические семейства. Для паракомпактных гиперболических сот существуют три группы в размерностях 6 и 9 , или, что эквивалентно, рангов 7 и 10, без других форм в более высоких размерностях. Из последних трех групп самой большой и важной является , которая связана с важной алгеброй Ли Каца–Муди . [4]
Системы счисления
Есть некоторые свидетельства, позволяющие предположить, что ранний человек мог использовать системы счета, которые состояли из «Один, Два, Три» и затем «Много» для описания пределов счета. У ранних людей было слово для описания количества одного, двух и трех, но любое количество сверх этого обозначалось просто как «Много». Это, скорее всего, основано на распространенности этого явления среди людей в таких разрозненных регионах, как глубокие джунгли Амазонки и Борнео, где исследователи западной цивилизации имеют исторические записи о своих первых встречах с этими коренными народами. [5]
Список основных расчетов
| Умножение | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 50 | 100 | 1000 | 10000 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 3 × х | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 | 27 | 30 | 33 | 36 | 39 | 42 | 45 | 48 | 51 | 54 | 57 | 60 | 63 | 66 | 69 | 72 | 75 | 150 | 300 | 3000 | 30000 |
| Разделение | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 3 ÷ х | 3 | 1.5 | 1 | 0,75 | 0,6 | 0,5 | 0.428571 | 0,375 | 0. 3 | 0.3 | 0. 27 | 0,25 | 0. 230769 | 0.2 142857 | 0.2 | 0,1875 | 0.1 7647058823529411 | 0,1 6 | 0.1 57894736842105263 | 0,15 | |
| х ÷ 3 | 0. 3 | 0. 6 | 1 | 1. 3 | 1. 6 | 2 | 2. 3 | 2. 6 | 3 | 3. 3 | 3. 6 | 4 | 4. 3 | 4. 6 | 5 | 5. 3 | 5. 6 | 6 | 6. 3 | 6. 6 |
| Возведение в степень | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 3 х | 3 | 9 | 27 | 81 | 243 | 729 | 2187 | 6561 | 19683 | 59049 | 177147 | 531441 | 1594323 | 4782969 | 14348907 | 43046721 | 129140163 | 387420489 | 1162261467 | 3486784401 | |
| х 3 | 1 | 8 | 27 | 64 | 125 | 216 | 343 | 512 | 729 | 1000 | 1331 | 1728 | 2197 | 2744 | 3375 | 4096 | 4913 | 5832 | 6859 | 8000 |
Наука
- Три — атомный номер лития .
- Три — это число измерений , которые могут воспринимать люди. Люди воспринимают вселенную как имеющую три пространственных измерения , но некоторые теории, такие как теория струн , предполагают, что их больше. [6]
- Три — число элементарных поколений фермионов согласно Стандартной модели физики элементарных частиц. [7]
- В физике элементарных частиц каждый протон или нейтрон состоит из трех кварков . [8]
- В аддитивной и субтрактивной моделях используются три основных цвета .
- Способность человеческого глаза различать цвета основана на различной чувствительности различных клеток сетчатки к свету с разной длиной волны . Поскольку люди трихроматичны , сетчатка содержит три типа цветовых рецепторных клеток, или колбочек . [9]
- В физике задачи трех тел не имеют общего замкнутого решения , в отличие от задач двух тел . [10]
Инженерное дело
- Треугольник , многоугольник с тремя ребрами и тремя вершинами , является наиболее устойчивой физической формой. По этой причине он широко используется в строительстве, инжиниринге и дизайне. [ 11]
Протонаука
- В европейской алхимии тремя основными элементами ( лат . tria prima ) были соль (
 ), сера (
), сера ( ) и ртуть (
) и ртуть ( ). [12] [13]
). [12] [13] - Три доши (слабости) и их противоядия являются основой аюрведической медицины в Индии. [14]
Псевдонаука
- Три — символическое представление затерянного континента Му , Огастеса Ле Плонжеона и Джеймса Черчворда . [15]
Философия
- Такие философы, как Фома Аквинский , Кант , Гегель , Чарльз Стерн Пирс и Карл Поппер , провели тройное деление, или трихотомию , которая сыграла важную роль в их работах. [ необходима ссылка ]
- Диалектика Гегеля Тезис + Антитезис = Синтез создает тройственность из двойственности. [ необходима цитата ]
- В интервью 1931 года Никола Тесла якобы сказал: «Если бы вы только знали величие чисел 3, 6 и 9, то у вас был бы ключ ко Вселенной». [ необходима цитата ]
Религия
This section needs additional citations for verification. (October 2023) |

Во многих мировых религиях присутствуют тройственные божества или концепции троицы, включая индуистских Тримурти и Тридеви , Триглава ( буквально «Трехглавый»), главного бога славян , три Драгоценности буддизма , трех Чистых даосизма , христианскую Святую Троицу и Тройственную Богиню Викки .

христианство
- Тройственное служение Христа — это христианское учение, которое гласит , что Христос выполняет функции пророка , священника и царя .
- Во время Страданий в саду Христос трижды просил, чтобы чаша миновала Его.
- Иисус воскрес из мертвых на третий день после своей смерти.
- Дьявол искушал Иисуса трижды.
- Святой Петр трижды отрекся от Иисуса и трижды подтвердил свою веру в Иисуса .
- Волхвы – мудрецы, которые были астрономами/астрологами из Персии [ 16] – преподнесли Иисусу три дара. [17] [18]
- Существует три синоптических Евангелия и три послания Иоанна .
- Апостол Павел ослеп на три дня после своего обращения в христианство .
иудаизм
- У Ноя было три сына: Хам , Сим и Иафет.
- Три патриарха : Авраам , Исаак и Иаков
- Пророк Валаам трижды бил свою ослицу.
- Пророк Иона провел три дня и ночи в чреве большой рыбы.
- Три раздела Письменной Торы : Тора (Пятикнижие Моисеево), Невиим (Пророки), Ктувим (Писания) [19]
- Три подразделения еврейского народа: Коэны , Левиты , Исраэль
- Три ежедневные молитвы : Шахарит , Минха , Маарив.
- Три шаббатних приема пищи
- Шаббат заканчивается, когда на ночном небе видны три звезды [20]
- Три паломнических праздника : Песах , Шавуот , Суккот
- Три мацы на пасхальном столе Седера [21]
- Три недели — период траура, соединяющий постные дни семнадцатого Тамуза и Тиша бе-Ава.
- Три главных греха, за которые еврей должен скорее умереть, чем согрешить: идолопоклонство , убийство , сексуальная распущенность [22]
- Апшерин , первая стрижка еврейского мальчика в возрасте 3 лет [23]
- Бет дин состоит из трех членов
- Потенциальных новообращенных традиционно отвергают три раза, чтобы проверить их искренность [24]
- В еврейской мистической традиции Каббалы считается, что душа состоит из трех частей, высшая из которых — нешама («дыхание»), средняя — руах («ветер» или «дух»), а низшая — нефеш («покой»). [25] Иногда дополнительно упоминаются два элемента : хая («жизнь» или «животное») и йехида («единица»).
- В Каббале Дерево Жизни (иврит: Эц ха-Хаим , עץ החיים) относится к последнему трехстолпному схематическому изображению его центрального мистического символа, известного как 10 сфирот .
ислам
- Три основных принципа шиитской традиции: Таухид (Единобожие), Набувва (Концепция пророчества), Имама (Концепция имама)
буддизм
- Тройной Бодхи (способы понимания конца рождения) — это Будху, Пасебудху и Махарахат.
- Три Драгоценности — три вещи, в которых буддисты находят прибежище.
Синтоизм
- Императорские регалии Японии: меч, зеркало и драгоценности.
даосизм
- Три сокровища ( кит .三寶; пиньинь : sānbǎo ; Уэйд-Джайлс : san-pao ), основные добродетели в даосизме .
- Три Даньтяня
- Три линии триграммы
- Три владыки : Небеса Фу Си (Рука – Голова – 3-й глаз), Человечество Шэнь Нун ( Отдел 69 ), Ад Нюйва (Нога – Живот – Пупок).
индуизм
- Тримурти : Брахма- Творец, Вишну- Хранитель и Шива- Разрушитель .
- Три гуны ( тригуна ) встречаются в школе санкхья индуистской философии. [26]
- Три пути к спасению в Бхагавад-гите называются Карма-йога , Бхакти-йога и Джняна-йога .
зороастризм
- Три добродетели Хумата , Хухта и Хуваршта (Благие мысли, Благие слова и Благие дела) являются основным принципом зороастризма .
Скандинавская мифология
Число три является очень значимым в скандинавской мифологии , наряду с его степенями 9 и 27.
- Перед Рагнарёк будут три суровые зимы без промежуточного лета, Фимбулвинтера .
- В своих поисках рун Один перенес три испытания на Мировом Древе : он повесился, ранил себя копьем и страдал от голода и жажды.
- У Бора было три сына: Один , Вили и Ве .
Другие религии
- Викканское правило трех .
- Триединая Богиня : Дева, Мать, Старуха; три судьбы.
- Сыновья Кроноса : Зевс , Посейдон и Аид .
- У славянского бога Триглава три головы.
Эзотерическая традиция
- Членство в Теософском обществе предполагает три условия .
- Три центра Гурджиева и Закон Трех .
- Liber AL vel Legis , центральное писание религии Телемы , состоит из трех глав, соответствующих трем божественным рассказчикам: Нуит , Хадит и Ра-Хор-Хуит .
- Тройственное величие Гермеса Трисмегиста — важная тема в герметизме .
Как счастливое или несчастливое число
This section needs additional citations for verification. (April 2009) |
Число три (三, официальное написание:叁, пиньинь sān , кантонский диалект : saam 1 ) считается хорошим числом в китайской культуре , поскольку оно звучит как слово «живой» (生pinyin shēng , кантонский диалект: saang 1 ), по сравнению с числом четыре (四, пиньинь sì , кантонский диалект: sei 1 ), которое звучит как слово «смерть» (死pinyin sǐ , кантонский диалект: sei 2 ).
Счет до трех распространен в ситуациях, когда группа людей хочет выполнить действие синхронно : Теперь , на счет три, все тянут! Предполагая, что счетчик идет с одинаковой скоростью, первые два счета необходимы для установления скорости, а счет «три» прогнозируется на основе времени «один» и «два» перед ним. Три, вероятно, используется вместо какого-то другого числа, потому что для этого требуется минимальное количество счетов при установлении скорости.
Есть еще одно суеверие, что не повезло взять третью зажигалку , то есть быть третьим человеком, который зажигает сигарету от той же спички или зажигалки. Иногда утверждается, что это суеверие возникло среди солдат в окопах Первой мировой войны, когда снайпер мог увидеть первую зажигалку, прицелиться во вторую и выстрелить в третью. [ необходима цитата ]
Фраза «Третий раз — это очарование» относится к суеверию, что после двух неудач в любом начинании третья попытка имеет больше шансов на успех. Это также иногда встречается в обратном порядке, как в «третий человек [что-то сделать, предположительно запрещенное] попадает». [ необходима цитата ]
Удача , особенно невезение, часто говорят, что «приходит по трое» [27] .
Смотрите также
- Куб (алгебра) – (3 верхних индекса )
- Трижды
- Третий
- Триада
- Трио
- Правило трех
- ɜ , U+025C ɜ ЛАТИНСКАЯ СТРОЧНАЯ БУКВА ПЕРЕВЕРНУТАЯ ОТКРЫТАЯ E также известная как перевернутый эпсилон
- Список автомагистралей под номером 3
Ссылки
- ^ Смит, Дэвид Юджин ; Карпински, Луис Чарльз (1911). Индо-арабские цифры. Бостон; Лондон: Ginn and Company. С. 27–29, 40–41.
- ^ Жорж Ифра, Всеобщая история чисел: от доисторических времен до изобретения компьютера , перевод Дэвида Беллоса и др. Лондон: The Harvill Press (1998): 393, рис. 24.63
- ↑ Прия Хеменуэй (2005), Божественная пропорция: Phi в искусстве, природе и науке , Sterling Publishing Company Inc., стр. 53–54, ISBN 1-4027-3522-7
- ^ Allcock, Daniel (май 2018 г.). «Prenilpotent Pairs in the E10 root grill» (PDF) . Mathematical Proceedings of the Cambridge Philosophical Society . 164 (3): 473–483. Bibcode :2018MPCPS.164..473A. doi :10.1017/S0305004117000287. S2CID 8547735. Архивировано (PDF) из оригинала 2022-11-03 . Получено 2022-11-03 .
- «Подробности предыдущего раздела были специфичны для E10, но та же философия, по всей видимости, применима и к другим симметризуемым гиперболическим корневым системам... кажется ценным дать схему того, как будут проходить вычисления», рассматривая E10 как модельный пример симметризуемости других корневых гиперболических систем En .
- ^ Гриббин, Мэри; Гриббин, Джон Р.; Эдни, Ральф; Холлидей, Николас (2003). Большие числа . Кембридж: Wizard. ISBN 1840464313.
- ^ Цвибах, Бартон (2009). Первый курс по теории струн (2-е изд.). Кембридж; Нью-Йорк: Cambridge University Press. ISBN 978-0-521-88032-9.
- ^ Харари, Х. (1977). "Три поколения кварков и лептонов" (PDF) . В ван Гоэлере, Э.; Вайнштейне, Р. (ред.). Труды XII Rencontre de Moriond . стр. 170. SLAC-PUB-1974.
- ^ Адэр, Р. К. (1989). Великий замысел: частицы, поля и творение . Oxford University Press . стр. 214. Bibcode : 1988gdpf.book.....A.
- ^ "Палочки и колбочки человеческого глаза". hyperphysics.phy-astr.gsu.edu . Получено 2024-06-04 .
- ^ Барроу-Грин, июнь (2008). «Проблема трех тел». В Gowers, Timothy; Барроу-Грин, июнь; Лидер, Имре (ред.). The Princeton Companion to Mathematics . Princeton University Press. стр. 726–728.
- ^ "Самая устойчивая форма — треугольник". Maths in the city . Получено 23 февраля 2015 г.
- ^ Эрик Джон Холмьярд. Алхимия. 1995. стр.153
- ^ Уолтер Дж. Фридлендер. Золотая палочка медицины: история символа кадуцея в медицине. 1992. С.76-77
- ^ Крейдлер, Марк (14.12.2017). «Аюрведа: Древнее суеверие, а не древняя мудрость». Skeptical Inquirer . Получено 04.06.2024 .
- ^ Чёрчворд, Джеймс (1931). «Затерянный континент Му – символы, виньетки, таблицы и диаграммы». Biblioteca Pleyades . Архивировано из оригинала 2015-07-18 . Получено 2016-03-15 .
- ^ Уиндл, Брайан (2022-12-22). «Кто были волхвы?». Отчет об археологии Библии . Получено 2024-07-05 .
- ^ "Британская энциклопедия". Lexikon des Gesamten Buchwesens Online (на немецком языке). дои : 10.1163/9789004337862_lgbo_com_050367.
- ^ "The Encyclopaedia Britannica". Nature . XV (378): 269–271. 25 января 1877 г. Архивировано из оригинала 24 июля 2020 г. Получено 12 июля 2019 г.
- ^ Маркус, раввин Йосси (2015). «Почему многие вещи в иудаизме делаются трижды?». Спросите Моисея . Архивировано из оригинала 2 апреля 2015 года . Получено 16 марта 2015 года .
- ^ "Shabbat". Иудаизм 101. 2011. Архивировано из оригинала 29 июня 2009. Получено 16 марта 2015 .
- ^ Китов, Элияху (2015). "Три мацы". Chabad.org . Архивировано из оригинала 24 марта 2015 года . Получено 16 марта 2015 года .
- ^ Каплан, раввин Арье (28 августа 2004 г.). «Иудаизм и мученичество». Aish.com. Архивировано из оригинала 20 марта 2015 г. Получено 16 марта 2015 г.
- ^ "Основы апшерина: первая стрижка мальчика". Chabad.org . 2015. Архивировано из оригинала 22 марта 2015. Получено 16 марта 2015 .
- ^ "Процесс обращения". Центр обращения в иудаизм. Архивировано из оригинала 23 февраля 2021 г. Получено 16 марта 2015 г.
- ^ Каплан, Арье. «Душа. Архивировано 24 февраля 2015 г. в Wayback Machine ». Айш . Из «Справочника еврейской мысли» (т. 2, издательство Maznaim . Перепечатано с разрешения.) 4 сентября 2004 г. Получено 24 февраля 2015 г.
- ↑ Джеймс Г. Лохтефельд, Гуна, в Иллюстрированной энциклопедии индуизма: AM, т. 1, Rosen Publishing, ISBN 978-0-8239-3179-8 , стр. 265
- ↑ См. «bad Архивировано 2009-03-02 в Wayback Machine » в Оксфордском словаре фраз и басен , 2006, через Encyclopedia.com.
- Уэллс, Д. Словарь любопытных и интересных чисел издательства Penguin . Лондон: Penguin Group. (1987): 46–48.
Внешние ссылки
- Трициклопедическая книга троек Майкла Эка
- Тройки в анатомии человека Джона А. Макналти
- Грайм, Джеймс. "3 везде". Numberphile . Брэди Харан . Архивировано из оригинала 2013-05-14 . Получено 2013-04-13 .
- Номер 3
- Положительное целое число 3
- Главные диковинки: 3