Иметь в виду

Среднее значение — это величина, представляющая «центр» набора чисел и являющаяся промежуточной по отношению к крайним значениям набора чисел. ^{[1] В} математике , особенно в статистике , существует несколько видов средних значений (или «мер центральной тенденции ») . Каждый из них пытается обобщить или типизировать заданную группу данных , иллюстрируя величину и знак набора данных . Какая из этих мер является наиболее показательной, зависит от того, что измеряется, а также от контекста и цели. ^[2]

Среднее арифметическое , также известное как «среднее арифметическое», представляет собой сумму значений, деленную на количество значений. Среднее арифметическое набора чисел x ₁ , x ₂ , ..., x _n обычно обозначается с помощью верхней черты , . ^{[примечание 1]} Если числа получены из наблюдения выборки большей группы , среднее арифметическое называется средним выборки ( ), чтобы отличить его от среднего значения группы (или ожидаемого значения ) базового распределения, обозначаемого или . ^{[примечание 2] [3]}${\displaystyle {\bar {x}}}$${\displaystyle {\bar {x}}}$${\displaystyle \мю}$${\displaystyle \mu _{x}}$

Помимо теории вероятностей и статистики, в геометрии и математическом анализе часто используется широкий спектр других понятий среднего значения ; примеры приведены ниже.

В математике три классических пифагорейских средних значения — это среднее арифметическое (AM), среднее геометрическое (GM) и среднее гармоническое (HM). Эти средние значения изучались с помощью пропорций пифагорейцами и последующими поколениями греческих математиков ^[4] из-за их важности в геометрии и музыке.

Среднее арифметическое (или просто среднее или среднее ) списка чисел — это сумма всех чисел, деленная на их количество. Аналогично, среднее значение выборки , обычно обозначаемое как , — это сумма выборочных значений, деленная на количество элементов в выборке.${\displaystyle x_{1},x_{2},\ldots ,x_{n}}$${\displaystyle {\bar {x}}}$

${\displaystyle {\bar {x}}={\frac {1}{n}}\left(\sum _{i=1}^{n}{x_{i}}\right)={\frac {x_{1}+x_{2}+\cdots +x_{n}}{n}}}$

Например, среднее арифметическое пяти значений: 4, 36, 45, 50, 75 равно:

${\displaystyle {\frac {4+36+45+50+75}{5}}={\frac {210}{5}}=42.}$

Среднее геометрическое — это среднее значение, которое полезно для наборов положительных чисел, которые интерпретируются в соответствии с их произведением (как в случае с темпами роста), а не их суммой (как в случае со средним арифметическим):

${\displaystyle {\bar {x}}=\left(\prod _{i=1}^{n}{x_{i}}\right)^{\frac {1}{n}}=\left(x_{1}x_{2}\cdots x_{n}\right)^{\frac {1}{n}}}$ ^[1]

Например, среднее геометрическое пяти значений: 4, 36, 45, 50, 75 равно:

${\displaystyle (4\times 36\times 45\times 50\times 75)^{\frac {1}{5}}={\sqrt[{5}]{24\;300\;000}}=30.}$

Гармоническое среднее — это среднее значение, которое полезно для наборов чисел, которые определены по отношению к некоторой единице , как в случае скорости (т. е. расстояния за единицу времени):

${\displaystyle {\bar {x}}=n\left(\sum _{i=1}^{n}{\frac {1}{x_{i}}}\right)^{-1}}$

Например, среднее гармоническое пяти значений: 4, 36, 45, 50, 75 равно

${\displaystyle {\frac {5}{{\tfrac {1}{4}}+{\tfrac {1}{36}}+{\tfrac {1}{45}}+{\tfrac {1}{ 50}}+{\tfrac {1}{75}}}}={\frac {5}{\;{\tfrac {1}{3}}\;}}=15.}$

Если у нас есть пять насосов, которые могут опорожнить резервуар определенного размера за 4, 36, 45, 50 и 75 минут соответственно, то среднее гармоническое значение говорит нам, что эти пять различных насосов, работающих вместе, будут качать с той же скоростью столько же, сколько пять насосов, каждый из которых может опорожнить резервуар за считанные минуты.${\displaystyle 15}$${\displaystyle 15}$

AM, GM и HM удовлетворяют следующим неравенствам: ^{[ необходима ссылка ]}

${\ displaystyle \ mathrm {AM} \ geq \ mathrm {GM} \ geq \ mathrm {HM} \,}$

Равенство имеет место, если все элементы данной выборки равны.

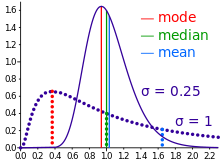
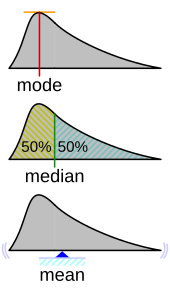
В описательной статистике среднее значение можно спутать с медианой , модой или средним диапазоном , поскольку любое из них может быть неправильно названо «средним» (более формально, мерой центральной тенденции ). Среднее значение набора наблюдений — это среднее арифметическое значений; однако для асимметричных распределений среднее значение не обязательно совпадает со средним значением (медианой) или наиболее вероятным значением (мода). Например, средний доход обычно смещен вверх небольшим числом людей с очень большими доходами, так что большинство имеет доход ниже среднего. Напротив, медианный доход — это уровень, на котором половина населения находится ниже, а половина — выше. Модальный доход — это наиболее вероятный доход, который благоприятствует большему числу людей с более низкими доходами. Хотя медиана и мода часто являются более интуитивными мерами для таких асимметричных данных, многие асимметричные распределения на самом деле лучше всего описываются их средним значением, включая экспоненциальное и пуассоновское распределения.

Среднее значение распределения вероятностей — это долгосрочное арифметическое среднее значение случайной величины , имеющей это распределение. Если случайная величина обозначается как , то среднее значение также известно как ожидаемое значение ( обозначается ). Для дискретного распределения вероятностей среднее значение задается как , где сумма берется по всем возможным значениям случайной величины и является функцией массы вероятности . Для непрерывного распределения среднее значение равно , где — функция плотности вероятности . ^[6] Во всех случаях, включая те, в которых распределение не является ни дискретным, ни непрерывным, среднее значение является интегралом Лебега случайной величины относительно ее меры вероятности . Среднее значение не обязательно должно существовать или быть конечным; для некоторых распределений вероятностей среднее значение бесконечно ( +∞ или −∞ ), в то время как для других среднее значение не определено .${\displaystyle X}$${\displaystyle X}$${\displaystyle E(X)}$${\displaystyle \textstyle \sum xP (x)}$${\displaystyle P(x)}$${\displaystyle \textstyle \int _{-\infty }^{\infty }xf(x)\,dx}$${\displaystyle f(x)}$

Обобщенное среднее , также известное как среднее степенное или среднее Гёльдера, является абстракцией квадратичного , арифметического, геометрического и гармонического среднего. Оно определяется для набора из n положительных чисел x _i как

${\displaystyle {\bar {x}}(m)=\left({\frac {1}{n}}\sum _{i=1}^{n}x_{i}^{m}\right)^{\frac {1}{m}}}$ ^[1]

Выбирая различные значения параметра m , получают следующие типы средних:

${\displaystyle \lim _{м\до \infty}}$

максимум​${\displaystyle x_{i}}$

${\displaystyle \lim _{м\до 2}}$

квадратичное среднее

${\displaystyle \lim _{м\до 1}}$

среднее арифметическое

${\displaystyle \lim _{м\до 0}}$

геометрическое среднее

${\displaystyle \lim _{м\к -1}}$

гармоническое среднее

${\displaystyle \lim _{м\к -\infty}}$

минимум​${\displaystyle x_{i}}$

Это можно обобщить далее как обобщенное f -среднее

${\displaystyle {\bar {x}}=f^{-1}\left({{\frac {1}{n}}\sum _{i=1}^{n}{f\left(x_{i}\right)}}\right)}$

и снова подходящий выбор обратимого f даст

${\displaystyle f(x)=x^{m}}$	мощность средняя ,
${\displaystyle f(x)=x}$	среднее арифметическое ,
${\displaystyle f(x)=\ln(x)}$	геометрическое среднее .
${\displaystyle f(x)=x^{-1}={\frac {1}{x}}}$	гармоническое среднее ,

Средневзвешенное арифметическое значение (или средневзвешенное значение) используется, если требуется объединить средние значения из выборок разного размера одной и той же совокупности:

${\displaystyle {\bar {x}}={\frac {\sum _{i=1}^{n}{w_{i}{\bar {x_{i}}}}}{\sum _{i=1}^{n}w_{i}}}.}$ ^[1]

Где и — среднее значение и размер выборки соответственно. В других приложениях они представляют собой меру надежности влияния соответствующих значений на среднее значение.${\displaystyle {\bar {x_{i}}}}$${\displaystyle w_{i}}$${\displaystyle я}$

Иногда набор чисел может содержать выбросы (т. е. значения данных, которые намного ниже или намного выше других). Часто выбросы представляют собой ошибочные данные, вызванные артефактами . В этом случае можно использовать усеченное среднее . Оно включает в себя отбрасывание заданных частей данных в верхней или нижней части, как правило, равное количество в каждой части, а затем взятие арифметического среднего оставшихся данных. Количество удаленных значений указывается как процент от общего количества значений.

Межквартильное среднее — это частный пример усеченного среднего. Это просто арифметическое среднее после удаления самой низкой и самой высокой четверти значений.

${\displaystyle {\bar {x}}={\frac {2}{n}}\;\sum _{i={\frac {n}{4}}+1}^{{\frac {3}{4}}n}\!\!x_{i}}$

если предположить, что значения были упорядочены, то это просто конкретный пример взвешенного среднего для определенного набора весов.

В некоторых обстоятельствах математики могут вычислять среднее значение бесконечного (или даже несчетного ) набора значений. Это может произойти при вычислении среднего значения функции . Интуитивно среднее значение функции можно представить как вычисление площади под участком кривой, а затем деление на длину этого участка. Это можно сделать грубо, подсчитав квадраты на миллиметровой бумаге, или, точнее, путем интегрирования . Формула интегрирования записывается как:${\displaystyle y_{\text{avg}}}$${\displaystyle f(x)}$

${\displaystyle y_{\text{avg}}(a,b)={\frac {1}{ba}}\int \limits _{a}^{b}\!f(x)\,dx}$

В этом случае необходимо следить за тем, чтобы интеграл сходился. Но среднее значение может быть конечным, даже если сама функция стремится к бесконечности в некоторых точках.

Углы , время суток и другие циклические величины требуют модульной арифметики для сложения и иного объединения чисел. Во всех этих ситуациях не будет уникального среднего значения. Например, время за час до и после полуночи равноудалено как от полуночи, так и от полудня. Также возможно, что среднего значения не существует. Рассмотрим цветовой круг — для набора всех цветов нет среднего значения. В этих ситуациях вы должны решить, какое среднее значение наиболее полезно. Вы можете сделать это, скорректировав значения перед усреднением или используя специализированный подход для среднего значения круговых величин .

Среднее Фреше дает способ определения «центра» распределения масс на поверхности или, в более общем смысле, римановом многообразии . В отличие от многих других средних, среднее Фреше определяется на пространстве, элементы которого не обязательно могут быть сложены или умножены на скаляры. Иногда его также называют средним Кархера (названным в честь Германа Кархера).

В геометрии существуют тысячи различных определений центра треугольника , которые все можно интерпретировать как среднее значение треугольного набора точек на плоскости. ^[7]

Это приближение к среднему значению для умеренно асимметричного распределения. ^[8] Оно используется при разведке углеводородов и определяется как:

${\displaystyle m=0,3P_{10}+0,4P_{50}+0,3P_{90}}$

где , и — 10-й, 50-й и 90-й процентили распределения соответственно.${\textstyle P_{10}}$${\textstyle P_{50}}$${\textstyle P_{90}}$

• Статистическая дисперсия
• Центральная тенденция
  • Медиана
  • Режим
• Описательная статистика
• Эксцесс
• Закон средних чисел
• Теорема о среднем значении
• Момент (математика)
• Сводная статистика
• Закон Тейлора