Среднеквадратичное значение
В математике среднеквадратичное значение (сокращенно RMS , RMS или rms ) набора чисел — это квадратный корень из среднего квадрата набора . [1] Для заданного набора его RMS обозначается как или . RMS также известно как квадратичное среднее (обозначается ), [2] [3] частный случай обобщенного среднего . RMS непрерывной функции обозначается и может быть определена в терминах интеграла квадрата функции.
Среднеквадратичное значение переменного электрического тока равно значению постоянного тока , который рассеивал бы ту же мощность в резистивной нагрузке . [1] В теории оценки среднеквадратичное отклонение оценщика измеряет, насколько далеко оценщик отклоняется от данных.
Определение
Среднеквадратичное значение набора значений (или непрерывной во времени формы волны ) является квадратным корнем из среднего арифметического квадратов значений или квадратом функции, которая определяет непрерывную форму волны. В физике среднеквадратичное значение тока может быть также определено как «значение постоянного тока, которое рассеивает ту же мощность в резисторе».
В случае набора из n значений среднеквадратичное отклонение равно
Соответствующая формула для непрерывной функции (или формы волны) f ( t ), определенной на интервале, имеет вид
а среднеквадратичное значение для функции за все время равно
Среднеквадратичное значение за все время периодической функции равно среднеквадратичному значению одного периода функции. Среднеквадратичное значение непрерывной функции или сигнала можно аппроксимировать, взяв среднеквадратичное значение выборки, состоящей из равномерно распределенных наблюдений. Кроме того, среднеквадратичное значение различных форм волн также можно определить без исчисления , как показал Картрайт. [4]
В случае среднеквадратической статистики случайного процесса вместо среднего значения используется ожидаемое значение .
В общих формах волн


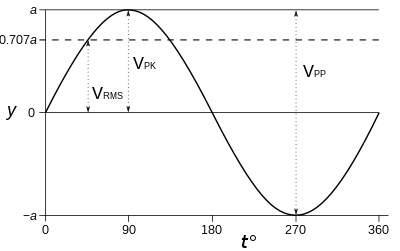
Если форма волны представляет собой чистую синусоиду , то соотношения между амплитудами (пик-пик, пик) и среднеквадратичной амплитудой фиксированы и известны, как и для любой непрерывной периодической волны. Однако это не относится к произвольной форме волны, которая может не быть ни периодической, ни непрерывной. Для синусоиды с нулевым средним соотношение между среднеквадратичной амплитудой и амплитудой от пика до пика следующее:
- От пика до пика
Для других форм волн соотношения не такие, как для синусоидальных волн. Например, для треугольной или пилообразной волны:
- От пика до пика
| Форма волны | Переменные и операторы | СКО |
|---|---|---|
| округ Колумбия | ||
| Синусоидальная волна | ||
| Прямоугольная волна | ||
| Прямоугольная волна со смещенным постоянным током | ||
| Модифицированная синусоида | ||
| Треугольная волна | ||
| Пилообразная волна | ||
| Пульсовая волна | ||
| Синусоидальная волна фаза-фаза | ||
где:
| ||
В комбинациях волновых форм
Формы волн, полученные путем суммирования известных простых форм волн, имеют среднеквадратичное значение, которое является корнем суммы квадратов среднеквадратических значений компонентов, если формы волн ортогональны ( то есть, если среднее значение произведения одной простой формы волны на другую равно нулю для всех пар, кроме формы волны, умноженной на саму себя). [5]
В качестве альтернативы, для волн, которые идеально положительно коррелируют или «синфазны» друг с другом, их среднеквадратичные значения суммируются напрямую.
Использует
В электротехнике
Напряжение
Частным случаем среднеквадратичного значения комбинаций волновых форм является: [6]
где относится к постоянному току (или среднему) компоненту сигнала, а — переменный ток сигнала.
Средняя электрическая мощность
Инженерам-электрикам часто требуется знать мощность , P , рассеиваемую электрическим сопротивлением , R. Легко выполнить расчет, когда через сопротивление протекает постоянный ток , I. Для нагрузки R Ом мощность определяется по формуле:
Однако, если ток является функцией, изменяющейся во времени, I ( t ), эта формула должна быть расширена, чтобы отразить тот факт, что ток (и, следовательно, мгновенная мощность) изменяется со временем. Если функция периодическая (например, мощность переменного тока в бытовых условиях), все равно имеет смысл обсуждать среднюю мощность, рассеиваемую со временем, которая рассчитывается путем взятия средней рассеиваемой мощности:
Таким образом, среднеквадратичное значение I RMS функции I ( t ) представляет собой постоянный ток, который обеспечивает такое же рассеивание мощности, как и усредненная по времени рассеиваемая мощность тока I ( t ).
Среднюю мощность можно также найти, используя тот же метод, что и в случае переменного во времени напряжения , V ( t ), со среднеквадратичным значением V RMS ,
Это уравнение можно использовать для любой периодической формы волны , например синусоидальной или пилообразной , что позволяет рассчитать среднюю мощность, подаваемую на определенную нагрузку.
Извлекая квадратный корень из обоих этих уравнений и перемножая их, получаем мощность:
Оба вывода зависят от пропорциональности напряжения и тока (то есть нагрузка R является чисто резистивной). Реактивные нагрузки (то есть нагрузки, способные не только рассеивать энергию, но и накапливать ее) обсуждаются в разделе « Мощность переменного тока» .
В общем случае переменного тока , когда I ( t ) представляет собой синусоидальный ток, что приблизительно верно для сетевого питания, среднеквадратичное значение легко вычислить из уравнения непрерывного случая выше. Если I p определяется как пиковый ток, то:
где t — время, а ω — угловая частота ( ω = 2 π / T , где T — период волны).
Так как I p — положительная константа и ее нужно было возвести в квадрат под знаком интеграла:
Использование тригонометрического тождества для устранения возведения в квадрат тригонометрической функции:
но поскольку интервал представляет собой целое число полных циклов (согласно определению RMS), синусоидальные члены сократятся, и останется:
Подобный анализ приводит к аналогичному уравнению для синусоидального напряжения:
где I P представляет собой пиковый ток, а V P представляет собой пиковое напряжение.
Из-за их полезности при выполнении расчетов мощности, перечисленные напряжения для розеток (например, 120 В в США или 230 В в Европе) почти всегда указываются в среднеквадратических значениях, а не пиковых значениях. Пиковые значения можно рассчитать из среднеквадратических значений по приведенной выше формуле, которая подразумевает V P = V RMS × √ 2 , предполагая, что источник представляет собой чистую синусоиду. Таким образом, пиковое значение напряжения сети в США составляет около 120 × √ 2 , или около 170 вольт. Напряжение от пика до пика, будучи в два раза больше, составляет около 340 вольт. Аналогичный расчет показывает, что пиковое напряжение сети в Европе составляет около 325 вольт, а напряжение от пика до пика — около 650 вольт.
Среднеквадратичные величины, такие как электрический ток, обычно рассчитываются за один цикл. Однако для некоторых целей при расчете потерь мощности передачи требуется среднеквадратичный ток за более длительный период. Применяется тот же принцип, и (например) ток в 10 ампер, используемый в течение 12 часов каждые 24 часа, представляет собой средний ток в 5 ампер, но среднеквадратичный ток в 7,07 ампер в долгосрочной перспективе.
Термин RMS-мощность иногда ошибочно используется (например, в аудиоиндустрии) как синоним средней мощности или средней мощности (она пропорциональна квадрату RMS-напряжения или RMS-тока в резистивной нагрузке). Для обсуждения измерений мощности звука и их недостатков см. Аудиомощность .
Скорость
В физике молекул газа среднеквадратическая скорость определяется как квадратный корень из средней квадратичной скорости. Среднеквадратичная скорость идеального газа рассчитывается с использованием следующего уравнения:
где R представляет собой газовую постоянную , 8,314 Дж/(моль·К), T — температура газа в кельвинах , а M — молярная масса газа в килограммах на моль. В физике скорость определяется как скалярная величина скорости. Для неподвижного газа средняя скорость его молекул может быть порядка тысяч км/ч, хотя средняя скорость его молекул равна нулю.
Ошибка
Когда сравниваются два набора данных — один набор из теоретического предсказания, а другой из фактического измерения некоторой физической переменной, например, — среднеквадратичное отклонение парных разностей двух наборов данных может служить мерой того, насколько в среднем ошибка от 0. Среднее значение абсолютных значений парных разностей может быть полезной мерой изменчивости разностей. Однако среднеквадратичное отклонение разностей обычно является предпочтительной мерой, вероятно, из-за математической условности и совместимости с другими формулами.
В частотной области
Среднеквадратичное значение можно вычислить в частотной области, используя теорему Парсеваля . Для дискретизированного сигнала , где - период дискретизации,
где и N — размер выборки, то есть количество наблюдений в выборке и коэффициенты ДПФ.
В этом случае среднеквадратичное значение, вычисленное во временной области, такое же, как и в частотной области:
Связь с другими статистическими данными

Если — среднее арифметическое , а — стандартное отклонение совокупности или формы волны , то: [7]
Из этого следует, что среднеквадратичное значение всегда больше или равно среднему значению, поскольку среднеквадратичное значение также включает в себя «ошибку» / квадратичное отклонение.
Ученые-физики часто используют термин «среднеквадратичное значение» как синоним стандартного отклонения , когда можно предположить, что входной сигнал имеет нулевое среднее значение, то есть ссылаясь на квадратный корень из среднеквадратичного отклонения сигнала от заданной базовой линии или подгонки. [8] [9] Это полезно для инженеров-электриков при расчете «только переменного тока» RMS сигнала. Стандартное отклонение является RMS колебания сигнала вокруг среднего значения, а не вокруг 0, постоянная составляющая удаляется (то есть RMS(сигнал) = stdev(сигнал), если средний сигнал равен 0).
Смотрите также
- Пифагорейское сложение
- Среднее выпрямленное значение (СВ)
- Центральный момент
- Геометрическое среднее
- L2 норма
- Наименьшие квадраты
- Словарь математических символов
- Среднеквадратичное смещение
- Истинный преобразователь RMS
Примечания
- ^ Если AC = a и BC = b . OC = AM точек a и b , и радиус r = QO = OG.
Используя теорему Пифагора , QC² = QO² + OC² ∴ QC = √ QO² + OC² = QM .
Используя теорему Пифагора, OC² = OG² + GC² ∴ GC = √ OC² − OG² = GM .
Используя подобные треугольники , ХК/ГК = ГК/ОК ∴ ХК = GC²/ОК = ГМ .
Ссылки
- ^ ab "Среднеквадратичное значение". Словарь физики (6-е изд.). Oxford University Press. 2009. ISBN 9780199233991.
- ^ Томпсон, Сильванус П. (1965). Calculus Made Easy. Macmillan International Higher Education. стр. 185. ISBN 9781349004874. Получено 5 июля 2020 г. .[ постоянная мертвая ссылка ]
- ^ Джонс, Алан Р. (2018). Вероятность, статистика и другие пугающие вещи. Routledge. стр. 48. ISBN 9781351661386. Получено 5 июля 2020 г. .
- ^ Картрайт, Кеннет В. (осень 2007 г.). «Определение эффективного или среднеквадратичного напряжения различных форм волн без исчисления» (PDF) . Интерфейс технологий . 8 (1): 20 страниц.
- ^ Настасе, Адриан С. «Как получить среднеквадратичное значение импульсных и прямоугольных сигналов». MasteringElectronicsDesign.com . Получено 21 января 2015 г.
- ^ "Make Better AC RMS Measurements with your Digital Multimeter" (PDF) . Keysight . Архивировано из оригинала (PDF) 15 января 2019 г. . Получено 15 января 2019 г. .
- ^ Крис С. Бисселл; Дэвид А. Чепмен (1992). Цифровая передача сигнала (2-е изд.). Cambridge University Press. стр. 64. ISBN 978-0-521-42557-5.
- ^ Вайсштейн, Эрик В. «Среднеквадратичное значение». MathWorld .
- ^ "ROOT, TH1:GetRMS". Архивировано из оригинала 2017-06-30 . Получено 2013-07-18 .
Внешние ссылки
- Почему термин RMS некорректен применительно к мощности звука
- Java-апплет для изучения RMS








![{\displaystyle f_{\text{RMS}}={\sqrt {{1 \over {T_{2}-T_{1}}}{\int _{T_{1}}^{T_{2}}{[f(t)]}^{2}\,{\rm {d}}t}}},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5e25b4df390e845aacaaa0c7dfd0ba6f1fc5cdde)
![{\displaystyle f_{\text{RMS}}=\lim _{T\rightarrow \infty }{\sqrt {{1 \over {2T}}{\int _{-T}^{T}{[f(t)]}^{2}\,{\rm {d}}t}}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8870ffec7ed1b4dfeb7f145630d2cecbe7b23b3e)


























![{\displaystyle {\begin{aligned}P_{\text{Avg}}&=\left(I(t)^{2}R\right)_{\text{Avg}}&&{\text{где }}(\cdots )_{\text{Avg}}{\text{ обозначает временное среднее значение функции}}\\[3pt]&=\left(I(t)^{2}\right)_{\text{Avg}}R&&{\text{(поскольку }}R{\text{ не меняется со временем, его можно вынести за скобки)}}\\[3pt]&=I_{\text{RMS}}^{2}R&&{\text{по определению среднеквадратичного значения}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/21b66c22138488b1a0487cfcb3763e3834e3a06b)


![{\displaystyle I_{\text{RMS}}={\sqrt {{1 \over {T_{2}-T_{1}}}\int _{T_{1}}^{T_{2}}\left[I_{\text{p}}\sin(\omega t)\right]^{2}dt}},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/df0578a1a0e325cba1139ef81b4867340cf0bf0c)

![{\displaystyle {\begin{aligned}I_{\text{RMS}}&=I_{\text{p}}{\sqrt {{1 \over {T_{2}-T_{1}}}{\int _{T_{1}}^{T_{2}}{1-\cos(2\omega t) \over 2}\,dt}}}\\[3pt]&=I_{\text{p}}{\sqrt {{1 \over {T_{2}-T_{1}}}\left[{t \over 2}-{\sin(2\omega t) \over 4\omega }\right]_{T_{1}}^{T_{2}}}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d6b151fc6495fb26320b04637150ff032c8d8797)
![{\displaystyle I_{\text{RMS}}=I_{\text{p}}{\sqrt {{1 \over {T_{2}-T_{1}}}\left[{t \over 2}\right]_{T_{1}}^{T_{2}}}}=I_{\text{p}}{\sqrt {{1 \over {T_{2}-T_{1}}}{{T_{2}-T_{1}} \over 2}}}={I_{\text{p}} \over {\sqrt {2}}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/45eaa1a04872567a59a8400a8f100a1debe34ec7)


![{\displaystyle x[n]=x(t=nT)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/de908f2452423bed903703e7bcdb147552d5859c)

![{\displaystyle \sum _{n=1}^{N}{x^{2}[n]}={\frac {1}{N}}\sum _{m=1}^{N}\left|X[m]\right|^{2},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0e5137ad83fb9b24095511bad31240b815a2d352)
![{\displaystyle X[m]=\operatorname {ДПФ} \{x[n]\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/12aee574790c3d79426ef841942408a85b1c8d3f)
![{\displaystyle {\text{RMS}}\{x[n]\}={\sqrt {{\frac {1}{N}}\sum _{n}{x^{2}[n]}}}={\sqrt {{\frac {1}{N^{2}}}\sum _{m}{{\bigl |}X[m]{\bigr |}}^{2}}}={\sqrt {\sum _{m}{\left|{\frac {X[m]}{N}}\right|^{2}}}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/aaa1cc81ec8221d7db02af033f2d5424c477a416)


