Гравитационная помощь
This article needs additional citations for verification. (May 2022) |
| Part of a series on |
| Astrodynamics |
|---|
Гравитационный маневр , гравитационный маневр , гравитационный облёт или, как его ещё называют, гравитационная праща в орбитальной механике — это тип пролёта космического корабля , при котором используется относительное движение (например, орбита вокруг Солнца ) и гравитация планеты или другого астрономического объекта для изменения траектории и скорости космического корабля , как правило, для экономии топлива и снижения расходов.
Гравитационное содействие может быть использовано для ускорения космического корабля, то есть для увеличения или уменьшения его скорости или изменения направления его пути. «Содействие» обеспечивается движением гравитирующего тела, когда оно тянет космический корабль. [1] Любое увеличение или потеря кинетической энергии и линейного импульса проходящим космическим кораблем соответственно теряется или приобретается гравитационным телом в соответствии с Третьим законом Ньютона . Гравитационный маневр был впервые использован в 1959 году, когда советский зонд Луна-3 сфотографировал обратную сторону Луны Земли , и он использовался межпланетными зондами, начиная с Маринера-10 , включая два известных пролета зондов Вояджер над Юпитером и Сатурном.
Объяснение

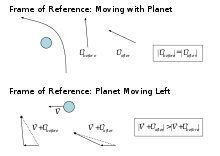
В системе отсчета планеты космический зонд уходит с той же скоростью, с которой он прибыл. Но при наблюдении в системе отсчета Солнечной системы (прикрепленной к Солнцу) выгода от этого маневра становится очевидной. Здесь можно увидеть, как зонд набирает скорость, черпая энергию из скорости планеты, вращающейся вокруг Солнца. (Если траектория спроектирована так, чтобы проходить перед планетой, а не позади нее, гравитационный маневр может использоваться как тормозной маневр, а не как ускорение.) Поскольку масса зонда на много порядков меньше массы планеты, в то время как результат на зонде весьма значителен, реакция замедления, испытываемая планетой, согласно третьему закону Ньютона , совершенно незаметна.
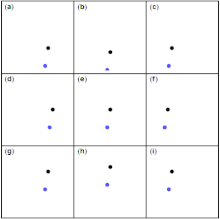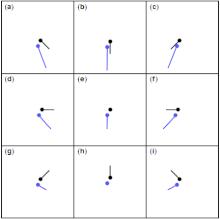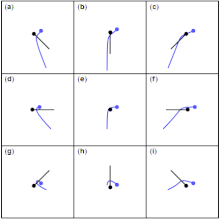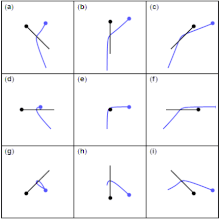
Гравитационный маневр вокруг планеты изменяет скорость космического корабля (относительно Солнца ) путем входа и выхода из гравитационной сферы влияния планеты. Сумма кинетических энергий обоих тел остается постоянной (см. упругое столкновение ). Поэтому маневр рогатки может быть использован для изменения траектории и скорости космического корабля относительно Солнца. [3]
Близкую земную аналогию дает теннисный мяч, отскакивающий от передней части движущегося поезда. Представьте, что вы стоите на платформе поезда и бросаете мяч со скоростью 30 км/ч в поезд, приближающийся со скоростью 50 км/ч. Машинист поезда видит, как мяч приближается со скоростью 80 км/ч, а затем отскакивает со скоростью 80 км/ч после того, как мяч упруго отскакивает от передней части поезда. Однако из-за движения поезда этот отскок происходит со скоростью 130 км/ч относительно платформы поезда; мяч добавил к своей собственной скорости в два раза больше скорости поезда. [4]
Переводя эту аналогию в космос: в системе отсчета планеты космический корабль имеет вертикальную скорость v относительно планеты. После того, как произойдет выстрел, космический корабль уходит по курсу, под углом 90 градусов к тому, по которому он прибыл. Он по-прежнему будет иметь скорость v , но в горизонтальном направлении. [2] В системе отсчета Солнца планета имеет горизонтальную скорость v, и, используя теорему Пифагора, космический корабль изначально имеет полную скорость √ 2 v . После того, как космический корабль покинет планету, он будет иметь скорость v + v = 2 v , набирая примерно 0,6 v . [2]
Этот упрощенный пример не может быть уточнен без дополнительных деталей относительно орбиты, но если космический корабль движется по траектории, которая образует гиперболу , он может покинуть планету в противоположном направлении, не запуская свой двигатель. Этот пример является одним из многих траекторий и наборов скорости, которые может испытать космический корабль.
Это объяснение может показаться нарушающим закон сохранения энергии и импульса, по-видимому, добавляя скорость космическому кораблю из ничего, но воздействие космического корабля на планету также должно быть принято во внимание, чтобы предоставить полную картину задействованной механики. Линейный импульс, приобретаемый космическим кораблем, равен по величине теряемому планетой, поэтому космический корабль приобретает скорость, а планета теряет скорость. Однако огромная масса планеты по сравнению с космическим кораблем делает результирующее изменение ее скорости пренебрежимо малым даже по сравнению с орбитальными возмущениями, которые планеты испытывают из-за взаимодействия с другими небесными телами в астрономически коротких временных масштабах. Например, одна метрическая тонна является типичной массой для межпланетного космического зонда, тогда как масса Юпитера составляет почти 2 x 10 24 метрических тонн. Следовательно, космический корабль весом в одну тонну, пролетающий мимо Юпитера, теоретически заставит планету потерять приблизительно 5 x 10 −25 км/с орбитальной скорости на каждый км/с скорости относительно Солнца, приобретаемой космическим кораблем. Для всех практических целей воздействие на планету можно игнорировать при расчетах. [5]
Реалистичные изображения встреч в космосе требуют рассмотрения трех измерений. Применяются те же принципы, что и выше, за исключением того, что добавление скорости планеты к скорости космического корабля требует сложения векторов, как показано ниже.
Благодаря обратимости орбит гравитационные пращи также могут использоваться для снижения скорости космического корабля. И Mariner 10 , и MESSENGER выполнили этот маневр, чтобы достичь Меркурия . [ необходима цитата ]
Если требуется больше скорости, чем доступно только за счет гравитационного маневра, то запуск ракеты вблизи перицентра (ближайшего планетарного сближения) потребляет меньше всего топлива. Заданный запуск ракеты всегда обеспечивает одинаковое изменение скорости ( Δv ), но изменение кинетической энергии пропорционально скорости транспортного средства в момент запуска. Поэтому максимальная кинетическая энергия получается, когда запуск происходит при максимальной скорости транспортного средства (перицентр). Эффект Оберта описывает эту технику более подробно.
Историческое происхождение
В своей статье «Тем , кто будет читать, чтобы строить» [6] , опубликованной в 1938 году, но датированной 1918–1919 годами, [a] Юрий Кондратюк предположил, что космический корабль, путешествующий между двумя планетами, может быть ускорен в начале и конце своей траектории с помощью гравитации лун двух планет. Часть его рукописи, рассматривающая гравитационные маневры, не получила дальнейшего развития и была опубликована только в 1960-х годах. [7] В своей статье 1925 года «Проблема полета при помощи реактивных аппаратов: межпланетные полеты» [ 8] Фридрих Цандер продемонстрировал глубокое понимание физики , лежащей в основе концепции гравитационного маневра, и его потенциала для межпланетного исследования Солнечной системы. [7]
Итальянский инженер Гаэтано Крокко первым рассчитал межпланетное путешествие с учетом множественных гравитационных маневров. [7]
Гравитационный маневр был впервые использован в 1959 году, когда советский зонд Луна-3 сфотографировал обратную сторону Луны. Маневр основывался на исследованиях, проведенных под руководством Мстислава Келдыша в Институте прикладной математики им. М. В. Келдыша . [9] [10] [11] [12]
В 1961 году Майкл Минович , аспирант Калифорнийского университета в Лос-Анджелесе , работавший в Лаборатории реактивного движения НАСА (JPL), разработал технику гравитационного маневра, которая позже была использована в идее Гранд-Планетарного тура Гэри Фландро . [ 13] [14]
Летом 1964 года в NASA JPL Гари Фландро получил задание изучить методы исследования внешних планет Солнечной системы. В этом исследовании он обнаружил редкое выравнивание внешних планет (Юпитера, Сатурна, Урана и Нептуна) и задумал многопланетную миссию Planetary Grand Tour, использующую гравитационный маневр для сокращения продолжительности миссии с сорока лет до менее чем десяти. [15]
Цель

Космический корабль, летящий с Земли на внутреннюю планету, увеличит свою относительную скорость, поскольку он падает в сторону Солнца, а космический корабль, летящий с Земли на внешнюю планету, уменьшит свою скорость, поскольку он покидает окрестности Солнца.
Хотя орбитальная скорость внутренней планеты больше, чем у Земли, космический корабль, летящий к внутренней планете, даже на минимальной скорости, необходимой для ее достижения, все равно ускоряется гравитацией Солнца до скорости, заметно превышающей орбитальную скорость этой планеты назначения. Если цель космического корабля — только пролететь мимо внутренней планеты, то обычно нет необходимости замедлять космический корабль. Однако, если космический корабль должен быть выведен на орбиту вокруг этой внутренней планеты, то должен быть какой-то способ замедлить его.
Аналогично, хотя орбитальная скорость внешней планеты меньше, чем у Земли, космический корабль, покидающий Землю на минимальной скорости, необходимой для путешествия к какой-то внешней планете, замедляется гравитацией Солнца до скорости, намного меньшей, чем орбитальная скорость этой внешней планеты. Следовательно, должен быть какой-то способ ускорить космический корабль, когда он достигает этой внешней планеты, если он должен выйти на орбиту вокруг нее.
Ракетные двигатели , безусловно, могут использоваться для увеличения и уменьшения скорости космического корабля. Однако тяга ракеты требует топлива, топливо имеет массу, и даже небольшое изменение скорости (известное как Δ v или «дельта- v », символ дельта используется для обозначения изменения, а «v» обозначает скорость ) приводит к гораздо большим требованиям к топливу, необходимому для выхода из гравитационного поля Земли . Это связано с тем, что двигатели первой ступени должны не только поднимать дополнительное топливо, но и поднимать дополнительное топливо сверх того, что необходимо для подъема этого дополнительного топлива. Требуемая масса для старта увеличивается экспоненциально с увеличением требуемой дельта- v космического корабля.
Поскольку для подъема топлива в космос требуется дополнительное топливо, космические миссии разрабатываются с жестким «бюджетом» топлива, известным как « бюджет дельта-v ». Бюджет дельта-v по сути является общим топливом, которое будет доступно после того, как вы покинете Землю, для ускорения, замедления, стабилизации против внешнего сотрясения (частицами или другими внешними эффектами) или изменения направления, если он не может получить больше топлива. Вся миссия должна быть спланирована в рамках этой возможности. Поэтому методы изменения скорости и направления, не требующие сжигания топлива, выгодны, поскольку они обеспечивают дополнительную маневренность и улучшение курса, не расходуя топливо из ограниченного количества, которое было доставлено в космос. Гравитационные маневры могут значительно изменить скорость космического корабля без расхода топлива и могут сэкономить значительное количество топлива, поэтому они являются очень распространенным методом экономии топлива.
Пределы
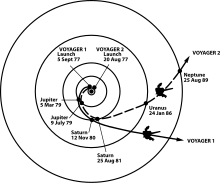
Главным практическим ограничением использования гравитационного маневра является то, что планеты и другие крупные массы редко находятся в нужных местах, чтобы обеспечить путешествие к определенному пункту назначения. Например, миссии Voyager , которые начались в конце 1970-х годов, стали возможными благодаря выравниванию " Grand Tour " Юпитера, Сатурна, Урана и Нептуна. Подобное выравнивание не повторится до середины 22-го века. Это крайний случай, но даже для менее амбициозных миссий бывают годы, когда планеты разбросаны по неподходящим частям своих орбит. [ требуется цитата ]
Другим ограничением является атмосфера, если таковая имеется, доступной планеты. Чем ближе космический корабль может приблизиться, тем выше его перицентрическая скорость, поскольку гравитация ускоряет космический корабль, позволяя получить больше кинетической энергии от сгорания ракеты. Однако, если космический корабль попадает слишком глубоко в атмосферу, энергия, потерянная на сопротивление, может превысить ту, что получена от гравитации планеты. С другой стороны, атмосфера может быть использована для выполнения аэроторможения . Также были теоретические предложения использовать аэродинамическую подъемную силу , когда космический корабль пролетает через атмосферу. Этот маневр, называемый аэрогравитационным ассистентом , может искривить траекторию на больший угол, чем одна только гравитация, и, следовательно, увеличить прирост энергии. [ необходима цитата ]
Даже в случае безвоздушного тела существует предел того, насколько близко может приблизиться космический корабль. Величина достижимого изменения скорости зависит от скорости сближения космического корабля и скорости выхода планеты в точке наибольшего сближения (ограниченной либо поверхностью, либо атмосферой). [ необходима цитата ]
Межпланетные пращи, использующие само Солнце, невозможны, поскольку Солнце находится в состоянии покоя относительно Солнечной системы в целом. Однако тяга вблизи Солнца имеет тот же эффект, что и активная праща, описанная как эффект Оберта . Это может значительно увеличить тяговую мощность космического корабля, но ограничено способностью космического корабля противостоять теплу. [ необходима цитата ]
Вращающаяся черная дыра может оказать дополнительную помощь, если ее ось вращения выровнена правильно. Общая теория относительности предсказывает, что большая вращающаяся масса производит увлечение кадра — вблизи объекта само пространство увлекается в направлении вращения. Любой обычный вращающийся объект производит этот эффект. Хотя попытки измерить увлечение кадра вокруг Солнца не дали четких доказательств, эксперименты, проведенные Gravity Probe B, обнаружили эффекты увлечения кадра, вызванные Землей. [16] Общая теория относительности предсказывает, что вращающаяся черная дыра окружена областью пространства, называемой эргосферой , в пределах которой стояние на месте (относительно вращения черной дыры) невозможно, потому что само пространство увлекается со скоростью света в том же направлении, что и вращение черной дыры. Процесс Пенроуза может предложить способ получения энергии из эргосферы, хотя для этого потребуется, чтобы космический корабль сбросил некоторый «балласт» в черную дыру, и космическому кораблю пришлось бы затратить энергию, чтобы доставить «балласт» в черную дыру. [ требуется ссылка ]
Известные примеры использования
- Луна 3
Впервые гравитационный маневр был предпринят в 1959 году для Луны-3 , чтобы сфотографировать обратную сторону Луны. [17] Спутник не набрал скорость, но его орбита была изменена таким образом, что это позволило успешно передать фотографии. [18]
- Пионер 10
Pioneer 10 от NASA — космический зонд, запущенный в 1972 году и выполнивший первую миссию к планете Юпитер . [19] После этого Pioneer 10 стал первым из пяти искусственных объектов , достигших скорости убегания, необходимой для того, чтобы покинуть Солнечную систему . В декабре 1973 года космический аппарат Pioneer 10 стал первым, кто использовал эффект гравитационной рогатки для достижения скорости убегания, необходимой для того, чтобы покинуть Солнечную систему. [20] [21]
- Пионер 11
Pioneer 11 был запущен NASA в 1973 году для изучения пояса астероидов , окружающей среды вокруг Юпитера и Сатурна , солнечных ветров и космических лучей . [19] Это был первый зонд , встретивший Сатурн , второй, пролетевший через пояс астероидов , и второй, пролетевший мимо Юпитера . Чтобы добраться до Сатурна, космический аппарат получил гравитационный маневр на Юпитере. [22] [23] [24]
- Маринер 10
Зонд Mariner 10 был первым космическим аппаратом, использовавшим эффект гравитационной рогатки для достижения другой планеты, пролетев мимо Венеры 5 февраля 1974 года на своем пути к тому, чтобы стать первым космическим аппаратом, исследовавшим Меркурий . [25]
- Вояджер 1
Voyager 1 был запущен NASA 5 сентября 1977 года. Он получил энергию, чтобы вырваться из гравитации Солнца, выполняя маневры с пращой вокруг Юпитера и Сатурна. [26] Проработав 47 лет, 1 месяц и 13 дней по состоянию на 18 октября 2024 года UTC [обновить] , космический аппарат по-прежнему связывается с Deep Space Network для получения обычных команд и передачи данных на Землю. Данные о расстоянии и скорости в реальном времени предоставляются [27] NASA и JPL. Находясь на расстоянии 152,2 а.е. (22,8 млрд км ; 14,1 млрд миль ) от Земли по состоянию на 12 января 2020 года [28] , он является самым удаленным от Земли объектом, созданным человеком. [29]
- Вояджер 2
Voyager 2 был запущен NASA 20 августа 1977 года для изучения внешних планет . Его траектория заняла больше времени, чтобы достичь Юпитера и Сатурна, чем у его близнеца-корабля, но позволила провести дальнейшие встречи с Ураном и Нептуном . [30]
- Галилео
Космический аппарат Galileo был запущен NASA в 1989 году и на своем пути к Юпитеру получил три гравитационных маневра, один от Венеры (10 февраля 1990 года) и два от Земли (8 декабря 1990 года и 8 декабря 1992 года). Космический аппарат достиг Юпитера в декабре 1995 года. Гравитационные маневры также позволили Galileo пролететь мимо двух астероидов, 243 Ида и 951 Гаспра . [31] [32]
- Улисс
В 1990 году НАСА запустило космический аппарат ESA Ulysses для изучения полярных областей Солнца. Все планеты вращаются примерно в плоскости, выровненной с экватором Солнца. Таким образом, чтобы выйти на орбиту, проходящую над полюсами Солнца, космическому аппарату пришлось бы исключить скорость, унаследованную им от орбиты Земли вокруг Солнца, и набрать скорость, необходимую для вращения вокруг Солнца в плоскости от полюса к полюсу. Это было достигнуто с помощью гравитационного маневра Юпитера 8 февраля 1992 года. [33] [34]
- ПОСЛАННИК
Миссия MESSENGER (запущенная в августе 2004 года) широко использовала гравитационные маневры для замедления скорости перед выходом на орбиту Меркурия. Миссия MESSENGER включала один пролет Земли, два пролета Венеры и три пролета Меркурия, прежде чем наконец прибыть на Меркурий в марте 2011 года со скоростью, достаточно низкой для выхода на орбиту с имеющимся топливом. Хотя пролеты были в основном орбитальными маневрами, каждый из них давал возможность для важных научных наблюдений. [35] [36]
- Кассини
Космический аппарат « Кассини -Гюйгенс» был запущен с Земли 15 октября 1997 года, за ним последовали гравитационные пролёты Венеры (26 апреля 1998 года и 21 июня 1999 года), Земли (18 августа 1999 года) и Юпитера (30 декабря 2000 года). Транзит к Сатурну занял 6,7 лет, космический аппарат прибыл 1 июля 2004 года. [37] [38] Его траектория была названа «Самой сложной гравитационной траекторией, пройденной на сегодняшний день» в 2019 году. [39]
После выхода на орбиту вокруг Сатурна космический аппарат Кассини использовал несколько гравитационных маневров Титана , чтобы также добиться значительных изменений в наклоне своей орбиты, так что вместо того, чтобы оставаться почти в экваториальной плоскости, траектория полета космического аппарата была наклонена далеко за пределы плоскости колец. [40] Типичное столкновение с Титаном изменяло скорость космического аппарата на 0,75 км/с, и космический аппарат совершил 127 столкновений с Титаном. Эти встречи позволили совершить орбитальный тур с широким диапазоном расстояний перицентра и апоцентра, различными выравниваниями орбиты по отношению к Солнцу и наклонами орбиты от 0° до 74°. Многочисленные пролеты Титана также позволили Кассини пролететь мимо других лун, таких как Рея и Энцелад . [ требуется ссылка ]
- Розетта
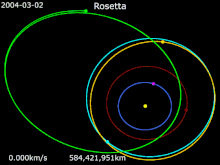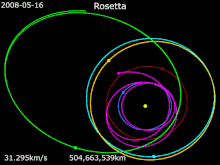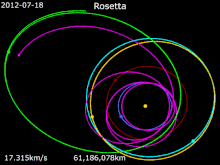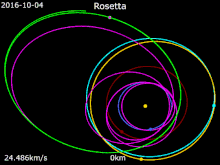
Зонд Rosetta , запущенный в марте 2004 года, использовал четыре гравитационных маневра (включая один всего в 250 км от поверхности Марса и три с Земли) для ускорения по всей внутренней Солнечной системе. Это позволило ему пролететь мимо астероидов 21 Лютеция и 2867 Штейнс , а также в конечном итоге достичь скорости кометы 67P/Чурюмова–Герасименко в точке встречи в августе 2014 года. [41] [42]
- Новые горизонты
New Horizons был запущен NASA в 2006 году и достиг Плутона в 2015 году. В 2007 году он выполнил гравитационный маневр на Юпитере. [43] [44]
- Юнона
Космический аппарат Juno был запущен 5 августа 2011 года (UTC). Траектория использовала гравитационное ускорение с Земли, достигнутое пролетом Земли в октябре 2013 года, через два года после его запуска 5 августа 2011 года. [45] Таким образом, Juno изменила свою орбиту (и скорость) по направлению к своей конечной цели, Юпитеру , всего через пять лет.
- Солнечный зонд Паркер
Parker Solar Probe , запущенный NASA в 2018 году, имеет семь запланированных гравитационных маневров на Венере. Каждый гравитационный маневр приближает Parker Solar Probe к Солнцу. По состоянию на 2022 год космический аппарат выполнил пять из семи своих маневров. Миссия Parker Solar Probe приблизится к Солнцу на самое близкое расстояние из всех космических миссий. [46] [47] [48]
- Солнечный Орбитер
Solar Orbiter был запущен ESA в 2020 году. На начальном этапе полета, который продлится до ноября 2021 года, Solar Orbiter выполнил два гравитационных маневра вокруг Венеры и один вокруг Земли, чтобы изменить траекторию космического корабля, направив его к самым внутренним областям Солнечной системы. Первый близкий солнечный проход состоится 26 марта 2022 года на расстоянии около трети расстояния Земли от Солнца. [49]
- BepiColombo
BepiColombo — совместная миссия Европейского космического агентства (ESA) и Японского агентства аэрокосмических исследований (JAXA) к планете Меркурий . Запуск состоялся 20 октября 2018 года. Он будет использовать технику гравитационного маневра с Землей один раз, с Венерой дважды и шесть раз с Меркурием . Он прибудет в 2025 году. BepiColombo назван в честь Джузеппе (Бепи) Коломбо , который был пионером в области такого способа маневрирования. [50]
- Люси
Lucy был запущен NASA 16 октября 2021 года. Он получил один гравитационный маневр от Земли 16 октября 2022 года [51] и после пролета астероида главного пояса 152830 Динкинеш он получит еще один в 2024 году. [52] В 2025 году он пролетит мимо внутреннего астероида главного пояса 52246 Дональдйохансон . [53] В 2027 году он прибудет в троянское облако L 4 ( греческий лагерь астероидов, который вращается примерно в 60° впереди Юпитера), где он пролетит мимо четырех троянцев, 3548 Эврибат (со своим спутником), 15094 Полимела , 11351 Левкус и 21900 Орус . [54] После этих пролетов Люси вернется на Землю в 2031 году для еще одного гравитационного маневра в направлении троянского облака L 5 ( троянский лагерь , который находится примерно в 60° позади Юпитера), где в 2033 году она посетит двойную звезду Троян 617 Патрокл со своим спутником Менетием .
Смотрите также
- 3753 Круитни , астероид, который периодически сталкивается с Землей посредством гравитационной пращи
- Бюджет Delta- v
- Низкоэнергетическая передача , тип гравитационного маневра, при котором космический аппарат гравитационно захватывается на орбиту небесным телом. Этот метод обычно применяется в системе Земля-Луна.
- Динамическое трение
- Аномалия пролета , аномальное увеличение дельта- v во время гравитационных маневров
- Гравитационная замочная скважина
- Межпланетная транспортная сеть
- n- проблема тела
- Эффект Оберта , применение тяги вблизи наибольшего сближения в гравитационном колодце
- Pioneer H , первая предложенная миссия за пределами эклиптики (OOE) для наблюдений за Юпитером и Солнцем.
- STEREO — миссия с использованием гравитации, которая использовала Луну для выведения двух космических аппаратов с орбиты Земли на гелиоцентрическую орбиту.
Примечания
- ^ В 1938 году, когда Кондратюк представил свою рукопись «Тому, кто будет читать, чтобы строить» для публикации, он датировал рукопись 1918–1919 годами, хотя было очевидно, что рукопись была пересмотрена в разное время. См. страницу 49 Технического перевода NASA F-9285 (1 ноября 1965 года).
Ссылки
- ^ ab "Раздел 1: Окружающая среда, Глава 4: Траектории". Основы космического полета. NASA . Получено 21 июля 2018 г.
- ^ abc "Gravity assist". Планетарное общество . Получено 1 января 2017 г.
- ^ "Пусть гравитация поможет вам ..." ESA . Получено 8 марта 2023 г.
- ^ "A Gravity Assist Primer". Основы космического полета. NASA . Получено 21 июля 2018 г.
- ^ Джонсон, RC (январь 2003 г.). Эффект рогатки (PDF) (Отчет). Университет Дарема. Архивировано из оригинала (PDF) 2020-08-01 . Получено 2018-07-21 .
- ↑ Статья Кондратюка включена в книгу: Мелькумов, Т.М., ред., Пионеры ракетной техники : Избранные труды (Москва, СССР: Институт истории естествознания и техники АН СССР, 1964). Английский перевод статьи Кондратюка был сделан NASA. См.: NASA Technical Translation F-9285, страницы 15–56 (1 ноября 1965 г.).
- ^ abc Negri, Rodolfo Batista; Prado, Antônio Fernando Bertachini de Alme (14 июля 2020 г.). «Исторический обзор теории гравитационных маневров в эпоху до космических полетов». Журнал Бразильского общества механических наук и инженерии . 42 (8). doi : 10.1007/s40430-020-02489-x . S2CID 220510617.
- ^ Статья Цандера 1925 года «Проблемы полета с помощью реактивного движения: межпланетные полеты» была переведена NASA. См. NASA Technical Translation F-147 (1964); в частности, Section 7: Flight Around a Planet's Satellite for Accelerating or Decelerating Spaceship, страницы 290–292.
- ^ Энеев, Т.; Аким, Э. «Мстислав Келдыш. Механика космического полета» // Институт прикладной математики им. М. В. Келдыша.
- ↑ Егоров, Всеволод Александрович (сентябрь 1957). «Конкретные вопросы полета на Луну». Успехи физических наук . 63 (9): 73–117. doi : 10.3367/UFNr.0063.195709f.0073 .
- ^ Раушенбах, Борис В.; Овчинников, Михаил Ю.; Маккенна-Лоулор, Сьюзен МП (2003). Essential Spaceflight Dynamics and Magnetospherics. Дордрехт , Нидерланды: Kluwer Academic . С. 146–147. ISBN 0-306-48027-1.
- ^ Бергер, Эрик (4 октября 2019 г.). «Да здравствует Луна-3, законный король космических миссий 1950-х годов». Ars Technica . Получено 13 октября 2023 г. .
- ^ «Математика, которая сделала возможным Voyager». BBC News . 22 октября 2012 г.
- ^ Портри, Дэвид СФ «Вызов планетам, часть третья: гравитация». Wired . Получено 5 декабря 2022 г.
- ^ Фландро, Гэри. «Быстрые разведывательные миссии во внешнюю часть Солнечной системы с использованием энергии, полученной из гравитационного поля Юпитера» (PDF) . GravityAssist.com . Получено 6 января 2024 г. .
- ^ Эверитт, К. В. Ф.; и др. (июнь 2011 г.). «Gravity Probe B: Final Results of a Space Experiment to Test General Relativity» (Гравитационный зонд B: окончательные результаты космического эксперимента по проверке общей теории относительности). Physical Review Letters . 106 (22). 221101. arXiv : 1105.3456 . Bibcode : 2011PhRvL.106v1101E. doi : 10.1103/PhysRevLett.106.221101. PMID 21702590. S2CID 11878715.
- ^ Негри, Родольфо Батиста; Прадо, Антонио Фернандо Бертакини де Алмейда (14 июля 2020 г.). «Исторический обзор теории гравитационных маневров в эпоху до космических полетов». Журнал Бразильского общества механических наук и инженерии . 42 (8): 406. doi :10.1007/s40430-020-02489-x. S2CID 220510617.
- ^ Сантос, Игнасио (2020). Моделирование и изучение гравитационных маневров (отчет).
- ^ ab Fimmel, RO; W. Swindell; E. Burgess (1974). SP-349/396 PIONEER ODYSSEY. NASA-Ames Research Center. SP-349/396 . Получено 9 января 2011 г. .
- ^ «Пусть гравитация поможет вам...» ScienceDaily . Получено 5 декабря 2022 г.
- ^ T. Franc (2011). "The Gravitational Assist". 20-я ежегодная конференция докторантов, WDS'11 "Неделя докторантов 2011", Карлов университет, факультет математики и физики, Прага, Чешская Республика, 31 мая 2011 г. - 3 июня 2011 г. : [материалы представленных докладов]. Pt. 3 Physics (PDF) (Вып. 1-е изд.). Прага: Matfyzpress. ISBN 978-80-7378-186-6. Получено 5 декабря 2022 г. .
- ^ "Pioneer 11: In Depth" . Получено 10 декабря 2017 г. .
- ↑ Марс, Келли (2 декабря 2019 г.). «45 лет назад Pioneer 11 исследует Юпитер». NASA . Получено 5 декабря 2022 г.
- ^ "Пионер 10 и 11, исследователи внешней солнечной системы". Планетарное общество . Получено 5 декабря 2022 г.
- ^ "In Depth | Mariner 10". NASA Solar System Exploration . Получено 5 декабря 2022 г.
- ^ "A Gravity Assist Primer". Основы космического полета. NASA . Получено 21 июля 2018 г.
- ^ «Вояджер — Статус миссии».
- ^ "Voyager – Mission Status". Jet Propulsion Laboratory . National Aeronautics and Space Administration . Получено 26 декабря 2019 г.,
- ^ "Voyager 1". BBC Solar System . Архивировано из оригинала 3 февраля 2018 года . Получено 4 сентября 2018 года .
- ^ Бутрика, Эндрю. От инженерной науки к большой науке. стр. 267. Получено 4 сентября 2015 г. Несмотря
на смену названия, Voyager во многом остался концепцией Grand Tour, хотя, конечно, не космическим аппаратом Grand Tour (TOPS).
Voyager 2
был запущен 20 августа 1977 года, а затем
Voyager 1
5 сентября 1977 года. Решение изменить порядок запуска было связано с сохранением возможности выполнения миссии Grand Tour к Урану, Нептуну и далее.
Voyager 2
, если бы его усилили максимальными характеристиками Titan-Centaur, едва мог бы догнать старую траекторию Grand Tour и встретиться с Ураном. Две недели спустя
Voyager 1
отправился бы по более легкой и гораздо более быстрой траектории, посетив только Юпитер и Сатурн.
Voyager 1
прибыл бы к Юпитеру на четыре месяца раньше Voyager 2, а затем прибыл бы к Сатурну на девять месяцев раньше. Таким образом, вторым запущенным космическим аппаратом был
Voyager 1
, а не
Voyager 2.
Два Voyager должны были прибыть к Сатурну с разницей в девять месяцев, так что если
Voyager 1
по какой-либо причине не достигнет своих целей на Сатурне,
Voyager 2
все равно можно было бы перенаправить на их достижение, хотя и за счет любого последующего столкновения с Ураном или Нептуном.
- ^ D'Amario, Louis A.; Bright, Larry E.; Wolf, Aron A. (май 1992). "Проектирование траектории Galileo". Space Science Reviews . 60 (1–4): 23. Bibcode : 1992SSRv...60...23D. doi : 10.1007/BF00216849. S2CID 122388506.
- ^ "Galileo Heads Towards Second Gravity Assist". Лаборатория реактивного движения NASA (JPL) . Получено 5 декабря 2022 г.
- ^ "ESA Science & Technology - Orbit of Ulysses". sci.esa.int . Получено 5 декабря 2022 г.
- ^ "ESA Science & Technology - Gravity Assist". sci.esa.int . Получено 5 декабря 2022 г.
- ^ "MESSENGER - Раскрытие тайн планеты Меркурий". messenger.jhuapl.edu . Получено 5 декабря 2022 г. .
- ^ "Ресурсы / Архивы новостей ИНФОРМАЦИЯ О FLYBY". messenger.jhuapl.edu . Получено 5 декабря 2022 г. .
- ^ "Траектория Кассини". NASA Solar System Exploration . Получено 5 декабря 2022 г.
 В данной статье использован текст из этого источника, находящегося в общественном достоянии .
В данной статье использован текст из этого источника, находящегося в общественном достоянии . - ^ "ESA Science & Technology - Getting to Saturn". sci.esa.int . Получено 5 декабря 2022 г. .
- ^ Беллероз, Джули; Рот, Дуэйн; Тарзи, Захи; Вагнер, Шон (2019). «Миссия Кассини: реконструкция тринадцати лет самой сложной траектории гравитационного маневра, пройденной на сегодняшний день». Космические операции: вдохновляя будущее человечества . Springer International Publishing. стр. 575–588. doi :10.1007/978-3-030-11536-4_22. ISBN 978-3-030-11535-7. S2CID 197554425 . Получено 5 декабря 2022 г. .
- ^ "Gravity Assists | Mission". NASA Solar System Exploration . Получено 5 декабря 2022 г.
 В данной статье использован текст из этого источника, находящегося в общественном достоянии .
В данной статье использован текст из этого источника, находящегося в общественном достоянии . - ^ "ESA Science & Technology - Rosetta Second Earth Swing-by". sci.esa.int . Получено 5 декабря 2022 г. .
- ^ Alexander, C.; Holmes, D.; Goldstein, R.; Parker, J. (2 марта 2008 г.). «Проект США Rosetta: гравитационный маневр на Марсе». IEEE Aerospace Conference 2008 г. стр. 1–9. doi :10.1109/AERO.2008.4526265. ISBN 978-1-4244-1487-1. S2CID 29248228.
- ^ Боэн, Брук. «NASA — Grand Theft Pluto: New Horizons получает импульс от пролета Юпитера». www.nasa.gov . Архивировано из оригинала 8 марта 2016 г. . Получено 5 декабря 2022 г. .
- ^ "New Horizons Jupiter Flyby". pds-atmospheres.nmsu.edu . Получено 5 декабря 2022 г. .
- ^ "Расписание запусков шаттлов и ракет НАСА". NASA . Получено 17 февраля 2011 г.
- ^ "Parker Solar Probe завершил свой пятый пролет вокруг Венеры – Parker Solar Probe". blogs.nasa.gov . 19 октября 2021 г. . Получено 5 декабря 2022 г. .
 В данной статье использован текст из этого источника, находящегося в общественном достоянии .
В данной статье использован текст из этого источника, находящегося в общественном достоянии . - ↑ Гарнер, Роб (4 октября 2018 г.). «Parker Solar Probe изменил правила игры еще до своего запуска». NASA . Получено 5 декабря 2022 г.
- ^ Го, Яньпин; Томпсон, Пол; Вирцбургер, Джон; Пинкин, Ник; Бушмен, Стюарт; Гудсон, Трой; Хоу, Роб; Хадсон, Джеймс; Джонс, Дрю; Киевски, Сет; Латроп, Брайан; Лау, Юнис; Моттингер, Нил; Райн, Марк; Шёнг, Вэнь-Йонг; Валерино, Поутауче; Уиттенбург, Карл (1 февраля 2021 г.). «Выполнение беспрецедентного полета Parker Solar Probe к Солнцу и первые результаты». Acta Astronautica . 179 : 425–438. Bibcode : 2021AcAau.179..425G. doi : 10.1016/j.actaastro.2020.11.007 . ISSN 0094-5765. S2CID 228944139.
- ^ "GMS: Solar Orbiter's Orbit". svs.gsfc.nasa.gov . 27 января 2020 г. Получено 14 февраля 2020 г.
 В данной статье использован текст из этого источника, находящегося в общественном достоянии .
В данной статье использован текст из этого источника, находящегося в общественном достоянии . - ^ "ESA Science & Technology BepiColombo". 28 июня 2022 г.
- ↑ Ли Канаяма (16 октября 2022 г.). «Люси завершает свой первый гравитационный маневр на Земле после года в космосе». www.nasaspaceflight.com . NASA Spaceflight.com . Получено 24 октября 2022 г. .
- ^ "NASA заключает контракт на пусковые услуги для миссии Lucy". nasa.gov . NASA. 31 января 2019 г. Получено 29 марта 2021 г.
 В данной статье использован текст из этого источника, находящегося в общественном достоянии .
В данной статье использован текст из этого источника, находящегося в общественном достоянии . - ^ Дрейер, Кейси; Лакдавалла, Эмили (30 сентября 2015 г.). «НАСА объявляет о пяти предложениях Discovery, отобранных для дальнейшего изучения». Планетарное общество.
- ^ Чанг, Кеннет (6 января 2017 г.). «Металлический шар размером с Массачусетс, который НАСА хочет исследовать». The New York Times .
Внешние ссылки
- Основы космического полета: Учебник по гравитационному маневру на NASA.gov
- Космический полет и космический корабль: Гравитационный маневр, обсуждение на Phy6.org
- «Гравитационная рогатка». MathPages.com .
- Эксперимент с двойным падением шарика

