Апсис
Апсида (от др.-греч. ἁψίς ( hapsís ) 'арка, свод'; мн . ч. apsides / ˈ æ p s ɪ ˌ d iː z / AP -sih-deez ) [1] [2] — самая дальняя или ближайшая точка орбиты планетного тела вокруг его основного тела . Линия апсид (также называемая апогеем) — это линия, соединяющая два крайних значения .
Апсиды, относящиеся к орбитам вокруг Солнца, имеют различные названия, чтобы отличать их от других апсид; эти названия — афелий для самой дальней и перигелий для самой ближайшей точки солнечной орбиты. [3] Две апсиды Луны — это самая дальняя точка, апогей , и ближайшая точка, перигей , ее орбиты вокруг хозяина Земли . Две апсиды Земли — это самая дальняя точка, афелий , и ближайшая точка, перигелий , ее орбиты вокруг хозяина Солнца. Термины афелий и перигелий применяются таким же образом к орбитам Юпитера и других планет , комет и астероидов Солнечной системы .
| Часть серии статей о |
| Астродинамика |
|---|
Общее описание

∗Периапсис и апоапсис как расстояния: наименьшее и наибольшее расстояния между орбитальным аппаратом и его телом-хозяином.
На любой эллиптической орбите есть две апсид . Название каждой апсиды образовано из префиксов ap- , apo- (от ἀπ(ό) , (ap(o)-) 'вдали от') для самой дальней или peri- (от περί (peri-) 'близко') для самой близкой точки к основному телу , с суффиксом, описывающим основное тело. Суффикс для Земли -gee , поэтому названия апсид - apogee и perigee . Для Солнца суффикс -helion , поэтому названия - aphelion и perihelion .
Согласно законам движения Ньютона , все периодические орбиты являются эллипсами. Центр масс двух тел может находиться внутри большего тела — например, центр масс Земли и Луны составляет около 75% пути от центра Земли до ее поверхности. [4] Если по сравнению с большей массой меньшая масса пренебрежимо мала (например, для спутников), то параметры орбиты не зависят от меньшей массы.
При использовании в качестве суффикса — то есть -apsis — этот термин может относиться к двум расстояниям от основного тела до вращающегося вокруг него тела, когда последнее расположено: 1) в точке перицентра или 2) в точке апоцентра (сравните оба графика, второй рисунок). Линия апсид обозначает расстояние линии, соединяющей ближайшую и самую дальнюю точки по всей орбите; она также относится просто к крайнему диапазону объекта, вращающегося вокруг тела-хозяина (см. верхний рисунок; см. третий рисунок).
В орбитальной механике апсидами технически называют расстояние, измеренное между барицентром системы из двух тел и центром масс орбитального тела. Однако в случае космического корабля эти термины обычно используются для обозначения орбитальной высоты космического корабля над поверхностью центрального тела (предполагая постоянный стандартный радиус отсчета).

Терминология
Часто встречаются слова «перицентр» и «апоцентр», хотя в техническом употреблении предпочтительнее термины «перицентр»/«апоцентр».
- В общих ситуациях, когда первичная точка не указана, термины перицентр и апоцентр используются для обозначения крайних точек орбит (см. таблицу, верхний рисунок); перицентр и апоцентр (или апапсис ) являются эквивалентными альтернативами, но эти термины также часто относятся к расстояниям, то есть наименьшему и наибольшему расстояниям между орбитальным аппаратом и его телом-носителем (см. второй рисунок).
- Для тела, вращающегося вокруг Солнца , точкой наименьшего расстояния является перигелий ( / ˌ p ɛr ɪ ˈ h iː l i ə n / ) , а точкой наибольшего расстояния является афелий ( / æ p ˈ h iː l i ə n / ) ; [5] при обсуждении орбит вокруг других звезд термины становятся периастром и апастроном .
- При обсуждении спутника Земли , включая Луну , точкой наименьшего расстояния является перигей ( / ˈ p ɛr ɪ dʒ iː / ), а точкой наибольшего расстояния — апогей (от древнегреческого : Γῆ ( Gē ), «земля» или «земля»). [6]
- Для объектов на лунной орбите точка наименьшего расстояния называется перицинтионом ( / ˌ p ɛr ɪ ˈ s ɪ n θ i ə n / ) , а наибольшего расстояния — апоцинтионом ( / ˌ æ p ə ˈ s ɪ n θ i ə n / ) . Также используются термины перилуния и апоселена , а также периселена и апоселена . [7] Поскольку у Луны нет естественных спутников, это применимо только к искусственным объектам.
Этимология
Слова перигелий и афелий были придуманы Иоганном Кеплером [8] для описания орбитальных движений планет вокруг Солнца. Слова образованы от префиксов пери- (греч. περί , около) и апо- (греч. ἀπό , вдали от), присоединенных к греческому слову, обозначающему Солнце, ( ἥλιος или hēlíos ). [5]
Различные связанные термины используются для других небесных объектов . Суффиксы -gee , -helion , -astron и -galacticon часто используются в астрономической литературе при упоминании Земли, Солнца, звезд и Галактического центра соответственно. Суффикс -jove иногда используется для Юпитера, но -saturnium очень редко использовался в последние 50 лет для Сатурна. Форма -gee также используется как общий термин для обозначения наибольшего приближения к «любой планете» — вместо того, чтобы применять его только к Земле.
Во время программы «Аполлон» термины «перицинтион» и «апокинтион» использовались применительно к орбите Луны ; они отсылают к Синтии, альтернативному имени греческой богини Луны Артемиды . [9] Совсем недавно, во время программы «Артемида» , использовались термины «перилуния» и «аполуния» . [10]
Что касается черных дыр, термин «периботрон» был впервые использован в статье 1976 года Дж. Фрэнка и М. Дж. Риза [11] , которые приписывают У. Р. Стоегеру предложение создать термин с использованием греческого слова, означающего «яма»: «ботрон».
Термины перимелазма и апомелазма (от греческого корня) были использованы физиком и автором научной фантастики Джеффри А. Лэндисом в рассказе, опубликованном в 1998 году [12] , таким образом, они появились раньше терминов perinigricon и aponigricon (от латинского) в научной литературе в 2002 году [13].
Терминология резюме
Суффиксы, показанные ниже, могут быть добавлены к префиксам peri- или apo- для формирования уникальных названий апсид для орбитальных тел указанной хост-/ (первичной) системы. Однако, только для систем Земля, Луна и Солнце обычно используются уникальные суффиксы. Исследования экзопланет обычно используют -astron , но, как правило, для других хост-систем вместо этого используется общий суффикс -apsis . [14] [ не удалось проверить ]
| Астрономический объект-хозяин | Суффикс | Происхождение названия |
|---|---|---|
| Солнце | -гелион | Гелиос |
| Меркурий | -гермион | Гермес |
| Венера | -цита | Киферийский |
| Земля | -ги | Гайя |
| Луна | -луна [7] -синтион -селен [7] | Луна Синтия Селена |
| Марс | -ареон | Арес |
| Церера | -деметра [15] | Деметра |
| Юпитер | -юпитер | Зевс Юпитер |
| Сатурн | -хрон [7] -кронос -сатурниум -крона [16] | Кронос Сатурн |
| Уран | -уранион | Уран |
| Нептун | -посейдеум [17] -посейдион | Посейдон |
| Астрономический объект-хозяин | Суффикс | Происхождение названия |
|---|---|---|
| Звезда | -астрон | Лат.: астра ; звезды |
| Галактика | -галактикон | Gr: galaxias; галактика |
| Барицентр | -центр -фокус -апсид | |
| Черная дыра | -мелазма -ботрон -нигрикон | Gr: melos; черный Gr: Bothros ; отверстие Lat: niger ; черный |
Перигелий и афелий

Перигелий (q) и афелий (Q) — это соответственно ближайшая и самая дальняя точки прямой орбиты тела вокруг Солнца .
Сравнение оскулирующих элементов в определенную эпоху с эффективными элементами в другую эпоху приведет к различиям. Время прохождения перигелия как один из шести оскулирующих элементов не является точным предсказанием (за исключением общей модели двух тел ) фактического минимального расстояния до Солнца с использованием полной динамической модели . Точные предсказания прохождения перигелия требуют численного интегрирования .
Внутренние планеты и внешние планеты
На двух изображениях ниже показаны орбиты, орбитальные узлы и положения перигелия (q) и афелия (Q) для планет Солнечной системы [18], как видно сверху северного полюса плоскости эклиптики Земли , которая копланарна с плоскостью орбиты Земли . Планеты движутся против часовой стрелки вокруг Солнца, и для каждой планеты синяя часть их орбиты проходит к северу от плоскости эклиптики, розовая часть — к югу, а точки обозначают перигелий (зеленый) и афелий (оранжевый).
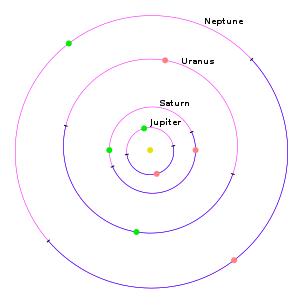
На первом изображении (внизу слева) показаны внутренние планеты, расположенные снаружи от Солнца, такие как Меркурий, Венера, Земля и Марс. Справочная земная орбита окрашена в желтый цвет и представляет собой орбитальную плоскость отсчета . Во время весеннего равноденствия Земля находится в нижней части рисунка. На втором изображении (внизу справа) показаны внешние планеты: Юпитер, Сатурн, Уран и Нептун.
Орбитальные узлы — это две конечные точки «линии узлов» , где наклонная орбита планеты пересекает плоскость отсчета; [19] здесь их можно «увидеть» как точки, где синяя часть орбиты встречается с розовой.
- Точки перигелия (зеленый) и афелия (оранжевый) внутренних планет Солнечной системы
- Точки перигелия (зеленый) и афелия (оранжевый) внешних планет Солнечной системы
Линии апсид
На диаграмме показан экстремальный диапазон — от самого близкого сближения (перигелия) до самой дальней точки (афелий) — нескольких вращающихся небесных тел Солнечной системы : планет, известных карликовых планет, включая Цереру , и кометы Галлея . Длина горизонтальных полос соответствует экстремальному диапазону орбиты указанного тела вокруг Солнца. Эти экстремальные расстояния (между перигелием и афелием) являются линиями апсид орбит различных объектов вокруг тела-хозяина.

Расстояния отдельных тел Солнечной системы от Солнца. Левый и правый края каждой полосы соответствуют перигелию и афелию тела, соответственно, поэтому длинные полосы обозначают высокий эксцентриситет орбиты . Радиус Солнца составляет 0,7 млн км, а радиус Юпитера (крупнейшей планеты) — 0,07 млн км, оба слишком малы, чтобы разрешить на этом изображении.
Перигелий и афелий Земли
В настоящее время Земля достигает перигелия в начале января, примерно через 14 дней после декабрьского солнцестояния . В перигелии центр Земли находится примерно0,983 29 астрономических единиц (AU) или 147 098 070 км (91 402 500 миль) от центра Солнца. Напротив, Земля достигает афелия в настоящее время в начале июля, примерно через 14 дней после июньского солнцестояния . Расстояние афелия между центрами Земли и Солнца в настоящее время составляет около1,016 71 а.е. или 152 097 700 км (94 509 100 миль).
Даты перигелия и афелия со временем меняются из-за прецессии и других орбитальных факторов, которые следуют циклическим закономерностям, известным как циклы Миланковича . В краткосрочной перспективе такие даты могут меняться до 2 дней из года в год. [20] Это значительное изменение обусловлено присутствием Луны: в то время как барицентр Земли и Луны движется по стабильной орбите вокруг Солнца, положение центра Земли, которое в среднем находится примерно в 4700 километрах (2900 миль) от барицентра, может быть смещено в любом направлении от него — и это влияет на время фактического наибольшего сближения между центрами Солнца и Земли (что, в свою очередь, определяет время перигелия в данном году). [21]
Из-за увеличенного расстояния в афелии только 93,55% излучения Солнца падает на данную область поверхности Земли, как и в перигелии, но это не учитывает времена года , которые возникают из-за наклона оси Земли на 23,4° от перпендикуляра к плоскости земной орбиты. [22] Действительно, и в перигелии, и в афелии в одном полушарии лето , а в другом — зима . Зима приходится на полушарие, куда солнечный свет падает меньше всего, а лето — на то полушарие, куда солнечный свет падает больше всего, независимо от расстояния Земли от Солнца.
В северном полушарии лето происходит в то же время, что и афелий, когда солнечная радиация самая низкая. Несмотря на это, лето в северном полушарии в среднем на 2,3 °C (4 °F) теплее, чем в южном полушарии, поскольку северное полушарие содержит более крупные массивы суши, которые легче нагревать, чем моря. [23]
Однако перигелий и афелий оказывают косвенное влияние на времена года: поскольку орбитальная скорость Земли минимальна в афелии и максимальна в перигелии, планете требуется больше времени для обращения по орбите от июньского солнцестояния до сентябрьского равноденствия, чем от декабрьского солнцестояния до мартовского равноденствия. Поэтому лето в северном полушарии длится немного дольше (93 дня), чем лето в южном полушарии (89 дней). [24]
Астрономы обычно выражают время перигелия относительно первой точки Овна не в днях и часах, а скорее как угол орбитального смещения, так называемую долготу периапсиса (также называемую долготой перицентра). Для орбиты Земли это называется долготой перигелия , и в 2000 году она составляла около 282,895°; к 2010 году она продвинулась на небольшую долю градуса до примерно 283,067°, [25] т. е. в среднем на 62" в год.
Для орбиты Земли вокруг Солнца время апсиды часто выражается через время относительно сезонов, поскольку это определяет вклад эллиптической орбиты в сезонные вариации. Изменчивость сезонов в первую очередь контролируется годовым циклом угла возвышения Солнца, который является результатом наклона оси Земли, измеренного от плоскости эклиптики . Эксцентриситет Земли и другие элементы орбиты не являются постоянными, а медленно изменяются из-за возмущающих эффектов планет и других объектов в солнечной системе (циклы Миланковича).
В очень длительной временной шкале даты перигелия и афелия прогрессируют по сезонам, и они делают один полный цикл за 22 000–26 000 лет. Существует соответствующее движение положения звезд, как видно с Земли, называемое прецессией апсид . (Это тесно связано с прецессией осей .) Даты и время перигелиев и афелиев для нескольких прошлых и будущих лет перечислены в следующей таблице: [26]
| Год | Перигелий | Афелий | ||
|---|---|---|---|---|
| Дата | Время ( всемирное время ) | Дата | Время ( всемирное время ) | |
| 2010 | 3 января | 00:09 | 6 июля | 11:30 |
| 2011 | 3 января | 18:32 | 4 июля | 14:54 |
| 2012 | 5 января | 00:32 | 5 июля | 03:32 |
| 2013 | 2 января | 04:38 | 5 июля | 14:44 |
| 2014 | 4 января | 11:59 | 4 июля | 00:13 |
| 2015 | 4 января | 06:36 | 6 июля | 19:40 |
| 2016 | 2 января | 22:49 | 4 июля | 16:24 |
| 2017 | 4 января | 14:18 | 3 июля | 20:11 |
| 2018 | 3 января | 05:35 | 6 июля | 16:47 |
| 2019 | 3 января | 05:20 | 4 июля | 22:11 |
| 2020 | 5 января | 07:48 | 4 июля | 11:35 |
| 2021 | 2 января | 13:51 | 5 июля | 22:27 |
| 2022 | 4 января | 06:55 | 4 июля | 07:11 |
| 2023 | 4 января | 16:17 | 6 июля | 20:07 |
| 2024 | 3 января | 00:39 | 5 июля | 05:06 |
| 2025 | 4 января | 13:28 | 3 июля | 19:55 |
| 2026 | 3 января | 17:16 | 6 июля | 17:31 |
| 2027 | 3 января | 02:33 | 5 июля | 05:06 |
| 2028 | 5 января | 12:28 | 3 июля | 22:18 |
| 2029 | 2 января | 18:13 | 6 июля | 05:12 |
Другие планеты
В следующей таблице показаны расстояния планет и карликовых планет от Солнца в их перигелии и афелии. [27]
| Тип кузова | Тело | Расстояние от Солнца в перигелии | Расстояние от Солнца в афелии | разница (%) | разница инсоляции (%) |
|---|---|---|---|---|---|
| Планета | Меркурий | 46 001 009 км (28 583 702 миль) | 69 817 445 км (43 382 549 миль) | 34% | 57% |
| Венера | 107 476 170 км (66 782 600 миль) | 108 942 780 км (67 693 910 миль) | 1,3% | 2.8% | |
| Земля | 147 098 291 км (91 402 640 миль) | 152 098 233 км (94 509 460 миль) | 3,3% | 6,5% | |
| Марс | 206 655 215 км (128 409 597 миль) | 249 232 432 км (154 865 853 миль) | 17% | 31% | |
| Юпитер | 740 679 835 км (460 237 112 миль) | 816 001 807 км (507 040 016 миль) | 9.2% | 18% | |
| Сатурн | 1349823615 км (838741509 миль) | 1503509229 км (934237322 миль) | 10% | 19% | |
| Уран | 2734998229 км (1,699449110 × 109 миль) | 3 006 318 143 км (1,868039489 × 10 9 миль) | 9.0% | 17% | |
| Нептун | 4 459 753 056 км (2,771162073 × 10 9 миль) | 4 537 039 826 км (2,819185846 × 10 9 миль) | 1,7% | 3,4% | |
| Карликовая планета | Церера | 380 951 528 км (236 712 305 миль) | 446 428 973 км (277 398 103 миль) | 15% | 27% |
| Плутон | 4 436 756 954 км (2,756872958 × 10 9 миль) | 7 376 124 302 км (4,583311152 × 10 9 миль) | 40% | 64% | |
| Хаумеа | 5 157 623 774 км (3,204798834 × 10 9 миль) | 7 706 399 149 км (4,788534427 × 10 9 миль) | 33% | 55% | |
| Makemake | 5 671 928 586 км (3,524373028 × 10 9 миль) | 7 894 762 625 км (4,905578065 × 10 9 миль) | 28% | 48% | |
| Эрис | 5 765 732 799 км (3,582660263 × 10 9 миль) | 14 594 512 904 км (9,068609883 × 10 9 миль) | 60% | 84% |
Математические формулы
Эти формулы характеризуют перицентр и апоцентр орбиты:
- Перицентр
- Максимальная скорость, , на минимальном (перицентрическом) расстоянии, .
- Апоцентр
- Минимальная скорость, , на максимальном (апоцентральном) расстоянии, .
В то время как в соответствии с законами Кеплера о движении планет (основанными на сохранении момента импульса ) и сохранении энергии эти две величины постоянны для данной орбиты:
где:
- это расстояние от апоцентра до первичного фокуса
- это расстояние от перицентра до первичного фокуса
- а — большая полуось :
- μ — стандартный гравитационный параметр
- e — эксцентриситет , определяемый как
Обратите внимание, что для преобразования высот над поверхностью в расстояния между орбитой и ее основным телом необходимо добавить радиус центрального тела, и наоборот.
Среднее арифметическое двух предельных расстояний есть длина большой полуоси a . Среднее геометрическое двух расстояний есть длина малой полуоси b .
Среднее геометрическое двух предельных скоростей равно
что является скоростью тела на круговой орбите, радиус которой равен .
Время перигелия
Орбитальные элементы, такие как время прохождения перигелия , определяются в выбранную эпоху с использованием невозмущенного решения для двух тел , которое не учитывает проблему n тел . Чтобы получить точное время прохождения перигелия, вам нужно использовать эпоху, близкую к прохождению перигелия. Например, при использовании эпохи 1996 года комета Хейла-Боппа покажет перигелий 1 апреля 1997 года. [28] Использование эпохи 2008 года показывает менее точную дату перигелия 30 марта 1997 года. [29] Короткопериодические кометы могут быть еще более чувствительны к выбранной эпохе. Использование эпохи 2005 года показывает, что 101P/Черных придет в перигелий 25 декабря 2005 года, [30] но использование эпохи 2012 года дает менее точную невозмущенную дату перигелия 20 января 2006 года. [31]
| Эпоха | Дата перигелия (tp) |
|---|---|
| 2010 | 2024-Апр-19.892 |
| n-тело [32] | 2024-Апр-21.139 |
| 2018 | 2024-Апр-23.069 |
Численное интегрирование показывает, что карликовая планета Эрида достигнет перигелия около декабря 2257 года. [33] Использование эпохи 2021 года, что на 236 лет раньше, менее точно показывает, что Эрида достигнет перигелия в 2260 году. [34]
4 Веста достигла перигелия 26 декабря 2021 года [35] , но использование решения двух тел в эпоху июля 2021 года менее точно показывает, что Веста достигла перигелия 25 декабря 2021 года. [36]
Короткие дуги
Транснептуновые объекты, обнаруженные на расстоянии 80+ а.е. от Солнца, нуждаются в десятках наблюдений в течение нескольких лет, чтобы хорошо ограничить их орбиты, поскольку они движутся очень медленно на фоне звезд. Из-за статистики малых чисел, транснептуновые объекты, такие как 2015 TH 367, когда у него было всего 8 наблюдений в течение дуги наблюдения в 1 год, которые не достигли или не достигнут перигелия примерно за 100 лет, могут иметь неопределенность в 1 сигму в 77,3 года (28 220 дней) в дате перигелия. [37]
Смотрите также
- Расстояние наибольшего сближения
- Эксцентрическая аномалия
- Пролёт (космический полёт)
- Гиперболическая траектория § Ближайшее приближение
- Средняя аномалия
- Перифокальная система координат
- Настоящая аномалия
Ссылки
- ^ "apsis". Dictionary.com Unabridged (Online). nd
- ^ "apsis". Американский словарь наследия английского языка (5-е изд.). HarperCollins.
- ↑ Джо Рао (6 июля 2023 г.). «Счастливого Дня афелия! Сегодня Земля находится дальше всего от Солнца в 2023 году». Space.com . Получено 22 апреля 2024 г. .
- ^ "Earth-Moon Barycenter - SkyMarvels.com". www.skymarvels.com . Получено 23 апреля 2024 г. .
- ^ ab Поскольку Солнце, Ἥλιος по-гречески, начинается с гласной (H — долгая гласная ē по-гречески), конечная o в «apo» опускается из префикса. = Произношение «Ap-helion» приводится во многих словарях [1] Архивировано 22 декабря 2015 г. на Wayback Machine , где «p» и «h» произносятся отдельными слогами. Однако произношение / ə ˈ f iː l i ə n / [2] Архивировано 29 июля 2017 г. на Wayback Machine также распространено ( например, McGraw Hill Dictionary of Scientific and Technical Terms, 5-е издание, 1994 г., стр. 114), поскольку в позднегреческом языке «p» от ἀπό, за которым следует «h» от ἥλιος, становится phi; таким образом, греческое слово — αφήλιον. (см., например, Walker, John, A Key to the Classical Pronunciation of Greek, Latin, and Scripture Proper Names , Townsend Young 1859 [3] Архивировано 21 сентября 2019 г. на Wayback Machine , стр. 26.) Многие [4] словари дают оба произношения
- ^ Чисхолм, Хью , ред. (1911). . Encyclopaedia Britannica . Том 21 (11-е изд.). Cambridge University Press. стр. 149.
- ^ abcd "Basics of Space Flight". NASA. Архивировано из оригинала 30 сентября 2019 г. Получено 30 мая 2017 г.
- ^ Кляйн, Эрнест, Полный этимологический словарь английского языка , Elsevier, Амстердам, 1965. (Архивная версия)
- ^ "Отчет о миссии Apollo 15". Глоссарий . Архивировано из оригинала 19 марта 2010 года . Получено 16 октября 2009 года .
- ^ R. Dendy; D. Zeleznikar; M. Zemba (27 сентября 2021 г.). NASA Lunar Exploration – Gateway's Power and Propulsion Element Communications Links. 38-я Международная конференция по спутниковым системам связи (ICSSC). Арлингтон, Вирджиния. Архивировано из оригинала 29 марта 2022 г. . Получено 18 июля 2022 г. .
- ^ Фрэнк, Дж.; Риз, М.Дж. (1 сентября 1976 г.). «Влияние массивных черных дыр на плотные звездные системы». MNRAS . 176 (6908): 633–646. Bibcode :1976MNRAS.176..633F. doi : 10.1093/mnras/176.3.633 .
- ↑ Perimelasma Архивировано 25 февраля 2019 г. в Wayback Machine , автор Джеффри Лэндис, впервые опубликовано в Asimov's Science Fiction , январь 1998 г., переиздано в Infinity Plus
- ^ R. Schödel; T. Ott; R. Genzel; R. Hofmann; M. Lehnert; A. Eckart; N. Mouawad; T. Alexander; MJ Reid; R. Lenzen; M. Hartung; F. Lacombe; D. Rouan; E. Gendron; G. Rousset; A.-M. Lagrange; W. Brandner; N. Ageorges; C. Lidman; AFM Moorwood; J. Spyromilio; N. Hubin; KM Menten (17 октября 2002 г.). «Звезда на 15,2-летней орбите вокруг сверхмассивной черной дыры в центре Млечного Пути». Nature . 419 (6908): 694–696. arXiv : astro-ph/0210426 . Bibcode :2002Natur.419..694S. doi :10.1038/nature01121. PMID 12384690. S2CID 4302128.
- ^ "MAVEN » Science Orbit". Архивировано из оригинала 8 ноября 2018 г. Получено 7 ноября 2018 г.
- ^ "Dawn Journal: 11 лет в космосе". www.planetary.org . Архивировано из оригинала 24 октября 2018 г. Получено 24 октября 2018 г.
- ^ Cecconi, B.; Lamy, L.; Zarka, P.; Prangé, R.; Kurth, WS; Louarn, P. (4 марта 2009 г.). «Гониополяриметрическое исследование перикрона вращения 29 с использованием высокочастотного радиоприемника инструмента Cassini Radio and Plasma Wave Science». Журнал геофизических исследований: космическая физика . 114 (A3): A03215. Bibcode : 2009JGRA..114.3215C. doi : 10.1029/2008JA013830. Архивировано из оригинала 9 декабря 2019 г. Получено 9 декабря 2019 г. – через ui.adsabs.harvard.edu.
- ^ Пример использования: Маккевитт, Джеймс; Булла, Софи; Диксон, Том; Крискола, Франко; Паркинсон-Свифт, Джонатан; Борнберг, Кристина; Сингх, Джасприт; Патель, Курен; Лаад, Ариан; Фордер, Итан; Айин-Уолш, Луис; Бигадхур, Шейн; Ведде, Пол; Паппула, Бхарат Симха Редди; Макдугалл, Томас; Фогис, Мадалин; Кент, Джек; Морган, Джеймс; Радж, Уткарш; Хайнрайхсбергер, Карина (18 июня 2021 г.). «Многоцелевая обсерватория и научная платформа класса L для Нептуна». Труды Всемирной конференции по исследованию космоса 2021 г. arXiv : 2106.09409 .
- ^ "определение апсиды". Dictionary.com . Архивировано из оригинала 8 декабря 2015 г. . Получено 28 ноября 2015 г. .
- ^ Дарлинг, Дэвид. "линия узлов". Энциклопедия астробиологии, астрономии и космических полетов . Архивировано из оригинала 23 августа 2019 г. Получено 17 мая 2007 г.
- ^ «Перигелий, афелий и солнцестояния». timeanddate.com. Архивировано из оригинала 3 января 2018 г. Получено 10 января 2018 г.
- ^ «Изменение времени перигелия и афелия». Отдел астрономических приложений Военно-морской обсерватории США. 11 августа 2011 г. Архивировано из оригинала 11 января 2018 г. Получено 10 января 2018 г.
- ^ "Исследование Солнечной системы: Наука и технологии: Научные особенности: погода, погода, везде?". NASA . Архивировано из оригинала 29 сентября 2015 г. Получено 19 сентября 2015 г.
- ^ "Земля в афелии". Космическая погода. Июль 2008. Архивировано из оригинала 17 июля 2015 года . Получено 7 июля 2015 года .
- ^ Рокпорт, Стив С. «Насколько афелий влияет на нашу погоду? Летом мы находимся в афелии. Было бы наше лето теплее, если бы мы были в перигелии?». Планетарий . Университет Южного Мэна . Архивировано из оригинала 6 июля 2020 г. . Получено 4 июля 2020 г.
- ^ "Data.GISS: Параметры орбиты Земли". data.giss.nasa.gov . Архивировано из оригинала 2 октября 2015 г.
- ^ Эспенак, Фред. «Земля в перигелии и афелии: с 2001 по 2100 год». astropixels . Архивировано из оригинала 13 июля 2021 г. . Получено 24 июня 2021 г. .
- ^ "NASA planetary comparison chart". Архивировано из оригинала 4 августа 2016 года . Получено 4 августа 2016 года .
- ^ "JPL SBDB: Hale-Bopp (Epoch 1996)". Архивировано из оригинала 16 июля 2020 г. Получено 16 июля 2020 г.
- ^ "JPL SBDB: Hale-Bopp". Архивировано из оригинала 17 июля 2020 г. Получено 16 июля 2020 г.
- ^ "101P/Черных – А (NK 1293) Сюичи Накано" . Архивировано из оригинала 3 октября 2020 года . Проверено 17 июля 2020 г.
- ^ JPL SBDB: 101P/Черных (эпоха 2012 г.)
- ^ "Horizons Batch for 12P/Pons-Brooks (90000223) at 2024-Apr-21 03:20" (Перигелий происходит, когда rdot переключается с отрицательного на положительный). JPL Horizons . Архивировано из оригинала 12 февраля 2023 г. Получено 11 февраля 2023 г.(JPL#K242/3 Дата солнца: 24 октября 2022 г.)
- ^ "Horizons Batch for Eris at perihelion about 7 December 2257 ±2 weeks". JPL Horizons (Перигелий происходит, когда rdot переключается с отрицательного на положительный. JPL SBDB в общем (неправильно) указывает невозмущенную дату двухтельного перигелия в 2260 году). Jet Propulsion Laboratory. Архивировано из оригинала 13 сентября 2021 г. Получено 13 сентября 2021 г.
- ^ "JPL SBDB: Eris (Epoch 2021)". Архивировано из оригинала 31 января 2018 г. Получено 5 января 2021 г.
- ^ "Horizons Batch for 4 Vesta on 2021-Dec-26" (Перигелий происходит, когда rdot переключается с отрицательного на положительный). JPL Horizons . Архивировано из оригинала 26 сентября 2021 г. Получено 26 сентября 2021 г.(Эпоха 2021-01 июля/Дата солнца: 2021-13 апреля)
- ^ JPL SBDB: 4 Веста (эпоха 2021 г.)
- ^ "JPL SBDB: 2015 TH367". Архивировано из оригинала 14 марта 2018 г. Получено 23 сентября 2021 г.
{{cite web}}: CS1 maint: bot: original URL status unknown (link)
Внешние ссылки
- Сравнение фотографических размеров апогея и перигея, perseus.gr
- Сравнение фотографических размеров афелия и перигелия, perseus.gr
- Времена года на Земле: равноденствия, солнцестояния, перигелий и афелий, 2000–2020 гг. Архивировано 13 октября 2007 г. на Wayback Machine , usno.navy.mil
- Даты и время перигелия и афелия Земли, 2000–2025 гг. Архивировано 13 октября 2007 г. на Wayback Machine из Военно-морской обсерватории США.
- Список астероидов, которые в настоящее время находятся ближе к Солнцу, чем Меркурий (Эти объекты будут близки к перигелию)
- Список JPL SBDB астероидов Главного пояса (H<8), отсортированный по дате перигелия