Орбита
В небесной механике орбита (также известная как орбитальное вращение ) — это криволинейная траектория объекта [1] , например, траектория планеты вокруг звезды, или естественного спутника вокруг планеты, или искусственного спутника вокруг объекта или положения в пространстве, такого как планета, луна, астероид или точка Лагранжа . Обычно орбита относится к регулярно повторяющейся траектории, хотя она может также относиться к неповторяющейся траектории. В близком приближении планеты и спутники следуют по эллиптическим орбитам , при этом центр масс находится на орбите в фокусной точке эллипса, [2], как описано законами движения планет Кеплера .
В большинстве ситуаций орбитальное движение адекватно аппроксимируется ньютоновской механикой , которая объясняет гравитацию как силу, подчиняющуюся закону обратных квадратов . [3] Однако общая теория относительности Альберта Эйнштейна , которая объясняет гравитацию как силу, обусловленную кривизной пространства-времени , с орбитами, следующими геодезическим линиям , обеспечивает более точный расчет и понимание точной механики орбитального движения.
История
.jpg/440px-Planisphaerium_Ptolemaicum_siue_machina_orbium_mundi_ex_hypothesi_Ptolemaica_in_plano_disposita_(2709983277).jpg)
Исторически, кажущиеся движения планет описывались европейскими и арабскими философами с использованием идеи небесных сфер . Эта модель постулировала существование идеальных движущихся сфер или колец, к которым были прикреплены звезды и планеты. Она предполагала, что небеса были зафиксированы отдельно от движения сфер, и была разработана без какого-либо понимания гравитации. После того, как движения планет были более точно измерены, были добавлены теоретические механизмы, такие как деферент и эпициклы . Хотя модель была способна достаточно точно предсказывать положения планет на небе, по мере того, как измерения становились более точными, требовалось все больше и больше эпициклов, поэтому модель становилась все более громоздкой. Первоначально геоцентрическая , она была изменена Коперником, чтобы поместить Солнце в центр, чтобы упростить модель. Модель была еще больше оспорена в 16 веке, когда наблюдались кометы, пересекающие сферы. [4] [5]

Основу современного понимания орбит впервые сформулировал Иоганн Кеплер , чьи результаты обобщены в его трех законах движения планет. Во-первых, он обнаружил, что орбиты планет в нашей Солнечной системе являются эллиптическими, а не круговыми (или эпициклическими ), как считалось ранее, и что Солнце находится не в центре орбит, а в одном из фокусов . [6] Во-вторых, он обнаружил, что орбитальная скорость каждой планеты не постоянна, как считалось ранее, а скорее зависит от расстояния планеты от Солнца. В-третьих, Кеплер обнаружил универсальную связь между орбитальными свойствами всех планет, вращающихся вокруг Солнца. Для планет кубы их расстояний от Солнца пропорциональны квадратам их орбитальных периодов. Например, Юпитер и Венера находятся на расстоянии около 5,2 и 0,723 а. е. от Солнца соответственно, их орбитальные периоды соответственно около 11,86 и 0,615 лет. Пропорциональность видна из того факта, что отношение для Юпитера, 5,2 3 /11,86 2 , практически равно отношению для Венеры, 0,723 3 /0,615 2 , в соответствии с соотношением. Идеализированные орбиты, соответствующие этим правилам, известны как орбиты Кеплера .
Исаак Ньютон продемонстрировал, что законы Кеплера выводятся из его теории гравитации и что, в общем случае, орбиты тел, подверженных гравитации, представляют собой конические сечения (это предполагает, что сила гравитации распространяется мгновенно). Ньютон показал, что для пары тел размеры орбит обратно пропорциональны их массам , и что эти тела вращаются вокруг общего центра масс . Когда одно тело намного массивнее другого (как в случае искусственного спутника, вращающегося вокруг планеты), удобным приближением является принятие центра масс как совпадающего с центром более массивного тела.
Достижения в области ньютоновской механики затем были использованы для изучения отклонений от простых предположений, лежащих в основе орбит Кеплера, таких как возмущения, вызванные другими телами, или воздействие сфероидальных, а не сферических тел. Жозеф-Луи Лагранж разработал новый подход к ньютоновской механике, подчеркивая энергию больше, чем силу, и добился прогресса в задаче трех тел , открыв точки Лагранжа . В драматическом оправдании классической механики в 1846 году Урбен Леверье смог предсказать положение Нептуна на основе необъяснимых возмущений в орбите Урана .
Альберт Эйнштейн в своей статье 1916 года « Основы общей теории относительности» объяснил, что гравитация обусловлена кривизной пространства-времени , и отменил предположение Ньютона о том, что изменения гравитации распространяются мгновенно. Это привело астрономов к признанию того, что ньютоновская механика не обеспечивает наивысшей точности в понимании орбит. В теории относительности орбиты следуют геодезическим траекториям, которые обычно очень хорошо аппроксимируются ньютоновскими предсказаниями (за исключением случаев, когда есть очень сильные гравитационные поля и очень высокие скорости), но различия измеримы. По сути, все экспериментальные свидетельства, которые могут различать теории, согласуются с теорией относительности в пределах точности экспериментальных измерений. Первоначальное подтверждение общей теории относительности заключается в том, что она смогла объяснить оставшуюся необъясненную величину в прецессии перигелия Меркурия, впервые отмеченную Леверье. Однако решение Ньютона по-прежнему используется для большинства краткосрочных целей, поскольку оно значительно проще в использовании и достаточно точно.
Планетарные орбиты
Этот раздел нуждается в дополнительных цитатах для проверки . ( Сентябрь 2020 ) |
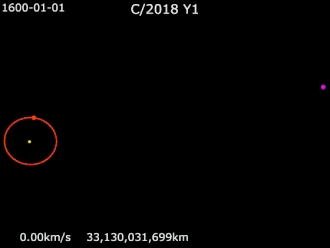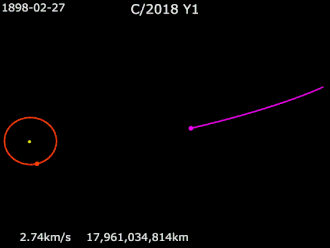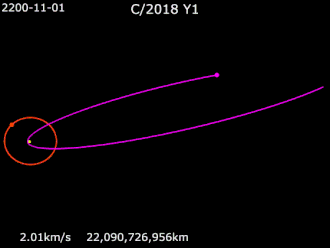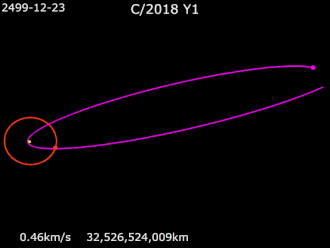
В планетной системе планеты, карликовые планеты , астероиды и другие малые планеты , кометы и космический мусор вращаются вокруг барицентра системы по эллиптическим орбитам . Комета на параболической или гиперболической орбите вокруг барицентра не связана гравитацией со звездой и, следовательно, не считается частью планетной системы звезды. Тела, которые гравитационно связаны с одной из планет в планетной системе, будь то естественные или искусственные спутники , следуют орбитам вокруг барицентра вблизи или внутри этой планеты.
Из-за взаимных гравитационных возмущений эксцентриситеты планетарных орбит меняются со временем. Меркурий , самая маленькая планета в Солнечной системе, имеет самую эксцентричную орбиту. В настоящую эпоху Марс имеет следующий по величине эксцентриситет, а самые маленькие эксцентриситеты орбит наблюдаются у Венеры и Нептуна .
Когда два объекта вращаются вокруг друг друга, перицентр — это точка, в которой два объекта находятся ближе всего друг к другу, а апоцентр — это точка, в которой они находятся дальше всего. (Для конкретных тел используются более конкретные термины. Например, перигей и апогей — это самая низкая и самая высокая части орбиты вокруг Земли, а перигелий и афелий — это самая близкая и самая дальняя точки орбиты вокруг Солнца.)
В случае планет, вращающихся вокруг звезды, масса звезды и всех ее спутников рассчитывается так, чтобы они находились в одной точке, называемой барицентром. Пути всех спутников звезды представляют собой эллиптические орбиты вокруг этого барицентра. Каждый спутник в этой системе будет иметь свою собственную эллиптическую орбиту с барицентром в одной из фокусных точек этого эллипса. В любой точке своей орбиты любой спутник будет иметь определенное значение кинетической и потенциальной энергии относительно барицентра, и сумма этих двух энергий является постоянным значением в каждой точке своей орбиты. В результате, когда планета приближается к перицентру , ее скорость будет увеличиваться по мере уменьшения ее потенциальной энергии; когда планета приближается к апоцентру , ее скорость будет уменьшаться по мере увеличения ее потенциальной энергии.
Принципы
Существует несколько распространенных способов понимания орбит:
- Сила, такая как гравитация, тянет объект по искривленной траектории, пытаясь лететь по прямой.
- Когда объект притягивается к массивному телу, он падает к этому телу. Однако, если у него достаточно тангенциальной скорости, он не упадет в тело, а вместо этого продолжит следовать по изогнутой траектории, вызванной этим телом, неопределенно долго. Тогда говорят, что объект вращается по орбите тела.
Таким образом, соотношение скоростей двух движущихся объектов с массой можно рассматривать в четырех практических классах с подтипами:
- Нет орбиты
- Суборбитальные траектории
- Диапазон прерывистых эллиптических траекторий
- Орбитальные траектории (или просто орбиты)
- Диапазон эллиптических траекторий с ближайшей точкой напротив точки стрельбы
- Круговой путь
- Диапазон эллиптических траекторий с ближайшей точкой в точке стрельбы
- Открытые (или эвакуационные) траектории
- Параболические траектории
- Гиперболические траектории
Орбитальные ракеты сначала запускаются вертикально, чтобы поднять ракету над атмосферой (что вызывает сопротивление трения), а затем медленно наклоняются и завершают работу ракетного двигателя параллельно атмосфере, чтобы достичь орбитальной скорости. [ необходима цитата ]
Оказавшись на орбите, их скорость удерживает их на орбите выше атмосферы. Если, например, эллиптическая орбита нырнет в плотный воздух, объект потеряет скорость и снова войдет в атмосферу (т. е. упадет). Иногда космический корабль намеренно пересекает атмосферу, в акте, который обычно называют маневром аэроторможения.
Иллюстрация

В качестве иллюстрации орбиты вокруг планеты может оказаться полезной модель пушечного ядра Ньютона (см. изображение ниже). Это « мысленный эксперимент », в котором пушка на вершине высокой горы способна стрелять пушечным ядром горизонтально с любой выбранной начальной скоростью. Влияние трения воздуха на пушечное ядро игнорируется (или, возможно, гора достаточно высока, чтобы пушка находилась выше атмосферы Земли, что одно и то же). [7]
Если пушка стреляет своим ядром с низкой начальной скоростью, траектория ядра искривляется вниз и ударяется о землю (A). По мере увеличения скорости стрельбы ядро ударяется о землю дальше (B) от пушки, потому что пока ядро все еще падает к земле, земля все больше и больше от него отклоняется (см. первый пункт выше). Все эти движения на самом деле являются «орбитами» в техническом смысле — они описывают часть эллиптической траектории вокруг центра тяжести — но орбиты прерываются ударом о Землю.
Если пушечное ядро выстреливается с достаточной скоростью, земля искривляется от ядра по крайней мере на столько же, на сколько падает ядро, поэтому ядро никогда не ударяется о землю. Теперь оно находится на том, что можно назвать непрерывной или круговой орбитой. Для любой конкретной комбинации высоты над центром тяжести и массы планеты существует одна конкретная скорость стрельбы (не зависящая от массы ядра, которая, как предполагается, очень мала по сравнению с массой Земли), которая создает круговую орбиту , как показано на (C).
По мере увеличения скорости стрельбы сверх этого значения образуются непрерывные эллиптические орбиты; одна из них показана на (D). Если начальная стрельба происходит над поверхностью Земли, как показано, то также будут непрерывные эллиптические орбиты с более низкой скоростью стрельбы; они будут ближе всего к Земле в точке на пол-витка дальше и прямо напротив точки стрельбы, ниже круговой орбиты.
При определенной горизонтальной скорости стрельбы, называемой скоростью убегания , зависящей от массы планеты и расстояния объекта от барицентра, достигается открытая орбита (E), имеющая параболическую траекторию . При еще больших скоростях объект будет следовать по ряду гиперболических траекторий . В практическом смысле оба этих типа траекторий означают, что объект «вырывается» из гравитации планеты и «улетает в космос», чтобы никогда не вернуться.
Законы движения Ньютона
Закон тяготения Ньютона и законы движения для задач двух тел
В большинстве ситуаций релятивистскими эффектами можно пренебречь, и законы Ньютона дают достаточно точное описание движения. Ускорение тела равно сумме сил, действующих на него, деленной на его массу, а сила тяготения, действующая на тело, пропорциональна произведению масс двух притягивающихся тел и уменьшается обратно пропорционально квадрату расстояния между ними. В этом ньютоновском приближении для системы двух точечных масс или сферических тел, находящихся под влиянием только их взаимного тяготения (называемой задачей двух тел ), их траектории могут быть точно рассчитаны. Если более тяжелое тело намного массивнее меньшего, как в случае спутника или небольшой луны, вращающихся вокруг планеты, или для Земли, вращающейся вокруг Солнца, достаточно точно и удобно описывать движение в терминах системы координат , которая центрирована на более тяжелом теле, и мы говорим, что более легкое тело находится на орбите вокруг более тяжелого. В случае, когда массы двух тел сравнимы, точное ньютоновское решение все еще достаточно и может быть получено путем помещения системы координат в центр масс системы.
Определение гравитационной потенциальной энергии
Энергия связана с гравитационными полями . Неподвижное тело, находящееся далеко от другого, может совершать внешнюю работу, если его притягивают к нему, и, следовательно, имеет гравитационную потенциальную энергию . Поскольку для разделения двух тел против силы тяжести требуется работа, их гравитационная потенциальная энергия увеличивается по мере их разделения и уменьшается по мере их сближения. Для точечных масс гравитационная энергия уменьшается до нуля по мере их приближения к нулевому разделению. Удобно и общепринято приписывать потенциальную энергию как имеющую нулевое значение, когда они находятся на бесконечном расстоянии друг от друга, и, следовательно, она имеет отрицательное значение (поскольку она уменьшается от нуля) для меньших конечных расстояний.
Орбитальные энергии и формы орбит
Когда взаимодействуют только два гравитационных тела, их орбиты следуют коническому сечению . Орбита может быть открытой (подразумевая, что объект никогда не возвращается) или закрытой (возвращающейся). Какая именно, зависит от полной энергии ( кинетическая + потенциальная энергия ) системы. В случае открытой орбиты скорость в любом положении орбиты по крайней мере равна скорости убегания для этого положения, в случае замкнутой орбиты скорость всегда меньше скорости убегания. Поскольку кинетическая энергия никогда не бывает отрицательной, если принято общее соглашение считать потенциальную энергию равной нулю при бесконечном разделении, связанные орбиты будут иметь отрицательную полную энергию, параболические траектории — нулевую полную энергию, а гиперболические орбиты — положительную полную энергию.
Открытая орбита будет иметь параболическую форму, если ее скорость в точности равна скорости убегания в этой точке траектории, и она будет иметь форму гиперболы, когда ее скорость больше скорости убегания. Когда тела со скоростью убегания или больше приближаются друг к другу, они на короткое время искривятся друг вокруг друга в момент их наибольшего сближения, а затем разойдутся навсегда.
Все замкнутые орбиты имеют форму эллипса . Круговая орбита является особым случаем, в котором фокусы эллипса совпадают. Точка, в которой движущееся по орбите тело находится ближе всего к Земле, называется перигеем , а при движении по орбите тела, отличного от Земли, она называется перицентром (менее правильно, «перифокусом» или «перицентром»). Точка, в которой спутник находится дальше всего от Земли, называется апогеем , апоцентром или иногда апифокусом или апоцентром. Линия, проведенная от перицентра к апоцентру, называется линией апсид . Это большая ось эллипса, линия, проходящая через его самую длинную часть.
Законы Кеплера
Тела, следующие по замкнутым орбитам, повторяют свои пути с определенным временем, называемым периодом. Это движение описывается эмпирическими законами Кеплера, которые можно математически вывести из законов Ньютона. Их можно сформулировать следующим образом:
- Орбита планеты вокруг Солнца представляет собой эллипс, в одной из фокусных точек которого находится Солнце. [Эта фокусная точка на самом деле является барицентром системы Солнце -планета ; для простоты это объяснение предполагает, что масса Солнца бесконечно больше массы этой планеты.] Орбита планеты лежит в плоскости, называемой орбитальной плоскостью . Точка на орбите, ближайшая к притягивающему телу, называется перицентром. Точка, наиболее удаленная от притягивающего тела, называется апоцентром. Существуют также специальные термины для обозначения орбит вокруг определенных тел; объекты, вращающиеся вокруг Солнца, имеют перигелий и афелий , объекты, вращающиеся вокруг Земли, имеют перигей и апогей , а объекты, вращающиеся вокруг Луны, имеют периселен и апоселен (или периселен и апоселен соответственно). Орбита вокруг любой звезды , не только Солнца, имеет периастрон и апастрон .
- По мере того, как планета движется по своей орбите, линия от Солнца до планеты заметает постоянную площадь орбитальной плоскости за определенный период времени, независимо от того, какую часть своей орбиты планета прослеживает за этот период времени. Это означает, что планета движется быстрее вблизи своего перигелия , чем вблизи своего афелия , потому что на меньшем расстоянии ей нужно проследить большую дугу, чтобы покрыть ту же площадь. Этот закон обычно формулируется как «равные площади за равное время».
- Для данной орбиты отношение куба ее большой полуоси к квадрату ее периода является постоянным.
Ограничения закона тяготения Ньютона
Обратите внимание, что в то время как связанные орбиты точечной массы или сферического тела с ньютоновским гравитационным полем являются замкнутыми эллипсами , которые повторяют один и тот же путь точно и бесконечно, любые несферические или неньютоновские эффекты (например, вызванные небольшим сжатием Земли или релятивистскими эффектами , тем самым изменяющими поведение гравитационного поля с расстоянием) приведут к тому, что форма орбиты будет отличаться от замкнутых эллипсов, характерных для ньютоновского движения двух тел . Решения для двух тел были опубликованы Ньютоном в Principia в 1687 году. В 1912 году Карл Фритьоф Сундман разработал сходящийся бесконечный ряд, который решает задачу трех тел ; однако он сходится слишком медленно, чтобы быть полезным. За исключением особых случаев, таких как точки Лагранжа , не известно ни одного метода решения уравнений движения для системы с четырьмя или более телами.
Подходы к решению задач многих тел
Вместо точного решения в замкнутой форме, орбиты со многими телами могут быть аппроксимированы с произвольно высокой точностью. Эти аппроксимации принимают две формы:
- Одна форма берет чистое эллиптическое движение за основу и добавляет члены возмущения для учета гравитационного влияния множественных тел. Это удобно для расчета положений астрономических тел. Уравнения движения лун, планет и других тел известны с большой точностью и используются для создания таблиц для небесной навигации . Тем не менее, существуют светские явления , с которыми приходится иметь дело постньютоновскими методами.
- Форма дифференциального уравнения используется в научных целях или для планирования миссий. Согласно законам Ньютона, сумма всех сил, действующих на тело, будет равна массе тела, умноженной на его ускорение ( F = ma ). Поэтому ускорения можно выразить в терминах положений. Члены возмущения гораздо проще описать в этой форме. Прогнозирование последующих положений и скоростей из начальных значений положения и скорости соответствует решению задачи с начальными значениями . Численные методы вычисляют положения и скорости объектов в короткое время в будущем, а затем повторяют расчет до тошноты. Однако крошечные арифметические ошибки из-за ограниченной точности компьютерной математики являются кумулятивными, что ограничивает точность этого подхода.
Дифференциальные симуляции с большим количеством объектов выполняют вычисления в иерархическом парном режиме между центрами масс. Используя эту схему, были смоделированы галактики, звездные скопления и другие большие скопления объектов. [8]
Ньютоновский анализ орбитального движения
Следующий вывод применим к такой эллиптической орбите. Мы начинаем только с закона тяготения Ньютона, утверждающего, что гравитационное ускорение по направлению к центральному телу обратно пропорционально квадрату расстояния между ними, а именно
где F 2 — сила, действующая на массу m 2 , вызванная гравитационным притяжением массы m 1 к m 2 , G — универсальная гравитационная постоянная, а r — расстояние между центрами двух масс.
Согласно Второму закону Ньютона, сумма сил, действующих на m 2 , связана с ускорением этого тела:
где A 2 — ускорение m 2 , вызванное силой гравитационного притяжения F 2 тела m 1 , действующей на m 2 .
Объединяем уравнения 1 и 2:
Решаем для ускорения A 2 :
где — стандартный гравитационный параметр , в данном случае . Подразумевается, что описываемая система — m 2 , поэтому индексы можно опустить.
Мы предполагаем, что центральное тело достаточно массивно, чтобы его можно было считать неподвижным, и игнорируем более тонкие эффекты общей теории относительности .
Когда маятник или объект, прикрепленный к пружине, колеблется по эллипсу, внутреннее ускорение/сила пропорциональны расстоянию Из-за способа сложения векторов, компонент силы в или в направлениях также пропорционален соответствующим компонентам расстояний, . Следовательно, весь анализ можно выполнить отдельно в этих измерениях. Это приводит к гармоническим параболическим уравнениям и эллипса.
Местоположение орбитального объекта в текущий момент времени определяется на плоскости с помощью векторного исчисления в полярных координатах как со стандартным евклидовым базисом, так и с полярным базисом с началом, совпадающим с центром силы. Пусть будет расстоянием между объектом и центром, а будет углом, на который он повернулся. Пусть и будут стандартными евклидовыми базисами, а и будут радиальным и поперечным полярными базисами, причем первый является единичным вектором, указывающим от центрального тела к текущему местоположению орбитального объекта, а второй является ортогональным единичным вектором, указывающим в направлении, в котором орбитальный объект будет двигаться, если будет вращаться по кругу против часовой стрелки. Тогда вектор к орбитальному объекту равен
Мы используем и для обозначения стандартных производных того, как это расстояние и угол изменяются со временем. Мы берем производную вектора, чтобы увидеть, как он изменяется со временем, вычитая его местоположение в момент времени из местоположения в момент времени и деля на . Результатом также является вектор. Поскольку наш базисный вектор движется по мере того, как объект вращается по орбите, мы начинаем с его дифференцирования. От времени до вектор сохраняет свое начало в начале координат и вращается от угла до , перемещая свою головку на расстояние в перпендикулярном направлении, давая производную от .
Теперь мы можем определить скорость и ускорение нашего орбитального объекта.
Коэффициенты и дают ускорения в радиальном и поперечном направлениях. Как уже было сказано, Ньютон дает этому первое из-за силы тяжести, а второе равно нулю.
| (1) |
| (2) |
Уравнение (2) можно преобразовать, используя интегрирование по частям.
Мы можем умножить на , потому что это не ноль, если только орбитальный объект не разобьется. Тогда, имея производную равной нулю, получаем, что функция является константой.
| (3) |
что на самом деле является теоретическим доказательством второго закона Кеплера (линия, соединяющая планету и Солнце, заметает равные площади за равные промежутки времени). Постоянная интегрирования, h , представляет собой момент импульса на единицу массы .
Чтобы получить уравнение для орбиты из уравнения (1), нам нужно исключить время. [9] (См. также уравнение Бине .) В полярных координатах это выразило бы расстояние орбитального объекта от центра как функцию его угла . Однако проще ввести вспомогательную переменную и выразить как функцию . Производные по времени можно переписать как производные по углу.
- (переработка (3))
Подставляя их в (1), получаем
| (4) |
Итак, для силы тяготения — или, в более общем смысле, для любого закона обратных квадратов силы — правая часть уравнения становится константой, и уравнение становится гармоническим уравнением (с точностью до сдвига начала координат зависимой переменной). Решение:
где A и θ 0 — произвольные константы. Это результирующее уравнение орбиты объекта — это уравнение эллипса в полярной форме относительно одной из фокусных точек. Это приводится к более стандартной форме, если принять эксцентриситет , который при перестановке мы видим:
Обратите внимание, что, если принять, что это большая полуось, а длинная ось эллипса направлена вдоль положительной координаты x , то получим:
Когда система из двух тел находится под действием крутящего момента, момент импульса h не является постоянной величиной. После следующего расчета:
мы получим уравнение Штурма-Лиувилля системы двух тел. [10]
| (5) |
Релятивистское орбитальное движение
Вышеуказанный классический ( ньютоновский ) анализ орбитальной механики предполагает, что более тонкие эффекты общей теории относительности , такие как затягивание системы отсчета и гравитационное замедление времени , незначительны. Релятивистские эффекты перестают быть незначительными вблизи очень массивных тел (как в случае прецессии орбиты Меркурия вокруг Солнца) или когда требуется чрезвычайная точность (как при расчетах орбитальных элементов и опорных сигналов времени для спутников GPS . [11] ).
Орбитальные плоскости
До сих пор анализ был двумерным; оказывается, что невозмущенная орбита является двумерной в плоскости, зафиксированной в пространстве, и, таким образом, расширение до трех измерений требует простого поворота двумерной плоскости на требуемый угол относительно полюсов соответствующего планетарного тела.
Для однозначного определения вращения в трех измерениях необходимы три числа; традиционно они выражаются в виде трех углов.
Период обращения
Орбитальный период — это время, необходимое телу, вращающемуся вокруг своей оси, для завершения одного оборота по орбите.
Указание орбит
Для задания кеплеровской орбиты вокруг тела требуется шесть параметров . Например, три числа, задающие начальное положение тела, и три значения, задающие его скорость, определят уникальную орбиту, которую можно рассчитать вперед (или назад) во времени. Однако традиционно используемые параметры немного отличаются.
Традиционно используемый набор орбитальных элементов называется набором кеплеровских элементов , в честь Иоганна Кеплера и его законов. Кеплеровских элементов шесть:
- Наклон ( я )
- Долгота восходящего узла (Ω)
- Аргумент перицентра (ω)
- Эксцентриситет ( e )
- Большая полуось ( а )
- Средняя аномалия в эпоху ( M 0 ).
В принципе, как только известны элементы орбиты тела, его положение можно вычислять вперед и назад до бесконечности во времени. Однако на практике орбиты подвергаются влиянию или возмущению другими силами, нежели простая гравитация от предполагаемого точечного источника (см. следующий раздел), и, таким образом, элементы орбиты со временем меняются.
Обратите внимание, что, если эксцентриситет не равен нулю, a не является средним радиусом орбиты. Усредненное по времени орбитальное расстояние определяется как: [12]
Возмущения
Орбитальное возмущение возникает, когда сила или импульс, значительно меньшие общей силы или среднего импульса основного гравитирующего тела и являющиеся внешними по отношению к двум вращающимся по орбите телам, вызывают ускорение, которое со временем изменяет параметры орбиты.
Радиальные, прогрессивные и поперечные возмущения
Небольшой радиальный импульс, приложенный к телу на орбите, изменяет эксцентриситет , но не орбитальный период (в первом порядке). Прямой или ретроградный импульс (т. е. импульс, приложенный вдоль орбитального движения) изменяет как эксцентриситет, так и орбитальный период . Примечательно, что прямой импульс в перицентре увеличивает высоту в апоцентре , и наоборот, а ретроградный импульс делает противоположное. Поперечный импульс (вне орбитальной плоскости) вызывает вращение орбитальной плоскости, не изменяя период или эксцентриситет. Во всех случаях замкнутая орбита все равно будет пересекать точку возмущения.
Орбитальный распад
Если орбита проходит вокруг планетарного тела со значительной атмосферой, ее орбита может затухать из-за сопротивления . В частности, в каждом перицентре объект испытывает атмосферное сопротивление, теряя энергию. Каждый раз орбита становится менее эксцентричной (более круговой), потому что объект теряет кинетическую энергию именно тогда, когда эта энергия максимальна. Это похоже на эффект замедления маятника в его самой низкой точке; самая высокая точка качания маятника становится ниже. С каждым последующим замедлением все большая часть траектории орбиты подвергается воздействию атмосферы, и эффект становится более выраженным. В конце концов, эффект становится настолько большим, что максимальной кинетической энергии недостаточно, чтобы вернуть орбиту выше пределов эффекта атмосферного сопротивления. Когда это происходит, тело будет быстро спирально опускаться и пересекать центральное тело.
Границы атмосферы сильно различаются. Во время солнечного максимума атмосфера Земли вызывает торможение на сто километров выше, чем во время солнечного минимума.
Некоторые спутники с длинными проводящими тросами также могут испытывать орбитальный спад из-за электромагнитного сопротивления магнитного поля Земли . Когда провод пересекает магнитное поле, он действует как генератор, перемещая электроны с одного конца на другой. Орбитальная энергия преобразуется в тепло в проводе.
На орбиты можно искусственно влиять с помощью ракетных двигателей, которые изменяют кинетическую энергию тела в какой-то точке его пути. Это преобразование химической или электрической энергии в кинетическую. Таким образом можно облегчить изменение формы или ориентации орбиты.
Другой метод искусственного влияния на орбиту — использование солнечных парусов или магнитных парусов . Эти формы движения не требуют никакого топлива или энергии, кроме энергии Солнца, и поэтому могут использоваться бесконечно. См. statite для одного из таких предлагаемых вариантов использования.
Орбитальный распад может происходить из-за приливных сил для объектов ниже синхронной орбиты для тела, вокруг которого они вращаются. Гравитация орбитального объекта поднимает приливные выпуклости в первичной, и поскольку ниже синхронной орбиты орбитальный объект движется быстрее, чем поверхность тела, выпуклости отстают на небольшой угол от него. Гравитация выпуклостей немного смещена от оси первичного спутника и, таким образом, имеет компонент вместе с движением спутника. Ближняя выпуклость замедляет объект больше, чем дальняя выпуклость ускоряет его, и в результате орбита затухает. И наоборот, гравитация спутника на выпуклостях прикладывает крутящий момент к первичной и ускоряет ее вращение. Искусственные спутники слишком малы, чтобы оказывать заметное приливное воздействие на планеты, вокруг которых они вращаются, но несколько лун в Солнечной системе претерпевают орбитальный распад по этому механизму. Ярким примером является ближайший к Марсу спутник Фобос , который, как ожидается, либо упадет на поверхность Марса, либо распадется на кольцо в течение 50 миллионов лет.
Орбиты могут распадаться из-за излучения гравитационных волн . Этот механизм крайне слаб для большинства звездных объектов, становясь значимым только в случаях, когда есть сочетание экстремальной массы и экстремального ускорения, например, в случае черных дыр или нейтронных звезд , которые вращаются друг вокруг друга на близком расстоянии.
Сплющенность
Стандартный анализ орбитальных тел предполагает, что все тела состоят из однородных сфер или, в более общем смысле, концентрических оболочек, каждая из которых имеет однородную плотность. Можно показать, что такие тела гравитационно эквивалентны точечным источникам.
Однако в реальном мире вращаются многие тела, и это вносит сплюснутость и искажает гравитационное поле, а также придает гравитационному полю квадрупольный момент, который имеет значение на расстояниях, сравнимых с радиусом тела. В общем случае гравитационный потенциал вращающегося тела, например, планеты, обычно расширяется в мультиполях, учитывающих отклонения его от сферической симметрии. С точки зрения динамики спутников особую значимость представляют так называемые четные зональные гармонические коэффициенты, или даже зональные, поскольку они вызывают вековые орбитальные возмущения, которые накапливаются в течение промежутков времени, превышающих орбитальный период. [13] [14] [15] Они зависят от ориентации оси симметрии тела в пространстве, влияя, в целом, на всю орбиту, за исключением большой полуоси.
Множественные гравитирующие тела
Влияние других гравитирующих тел может быть значительным. Например, орбиту Луны невозможно точно описать, не принимая во внимание действие гравитации Солнца, а также Земли. Один приблизительный результат заключается в том, что тела обычно будут иметь достаточно стабильные орбиты вокруг более тяжелой планеты или луны, несмотря на эти возмущения, при условии, что они вращаются в пределах сферы Хилла более тяжелого тела .
Когда имеется более двух гравитирующих тел, это называется проблемой n-тел . Большинство проблем n-тел не имеют решения в замкнутой форме , хотя были сформулированы некоторые особые случаи.
Световое излучение и звездный ветер
Для меньших тел, в частности, свет и звездный ветер могут вызывать значительные возмущения в отношении и направлении движения тела, и со временем могут быть значительными. Из планетарных тел движение астероидов особенно подвержено влиянию в течение больших периодов, когда астероиды вращаются относительно Солнца.
Странные орбиты
Математики обнаружили, что в принципе возможно иметь несколько тел на неэллиптических орбитах, которые периодически повторяются, хотя большинство таких орбит не являются стабильными относительно малых возмущений массы, положения или скорости. Однако были выявлены некоторые особые стабильные случаи, включая плоскую орбиту в форме восьмерки, занятую тремя движущимися телами . [16] Дальнейшие исследования обнаружили, что неплоские орбиты также возможны, включая одну, включающую 12 масс, движущихся по 4 примерно круговым, переплетающимся орбитам, топологически эквивалентным ребрам кубооктаэдра . [ 17]
Считается, что обнаружение таких орбит, естественным образом возникающих во Вселенной, крайне маловероятно из-за маловероятности случайного возникновения требуемых условий. [17]
Астродинамика
Орбитальная механика или астродинамика — это приложение баллистики и небесной механики к практическим проблемам, касающимся движения ракет и других космических аппаратов . Движение этих объектов обычно рассчитывается на основе законов движения Ньютона и закона всемирного тяготения Ньютона . Это основная дисциплина в проектировании и управлении космическими миссиями. Небесная механика рассматривает более широко орбитальную динамику систем, находящихся под влиянием гравитации , включая космические аппараты и естественные астрономические тела, такие как звездные системы, планеты , луны и кометы . Орбитальная механика фокусируется на траекториях космических аппаратов , включая орбитальные маневры , изменения плоскости орбиты и межпланетные переходы, и используется планировщиками миссий для прогнозирования результатов пропульсивных маневров . Общая теория относительности является более точной теорией, чем законы Ньютона, для расчета орбит и иногда необходима для большей точности или в ситуациях с высокой гравитацией (например, на орбитах, близких к Солнцу).
Орбиты Земли
- Низкая околоземная орбита (НОО): геоцентрические орбиты с высотами до 2000 км (0–1240 миль ). [18]
- Средняя околоземная орбита (MEO): геоцентрические орбиты высотой от 2000 км (1240 миль ) до чуть ниже геосинхронной орбиты на высоте 35 786 километров (22 236 миль). Также известны как промежуточные круговые орбиты . Они «чаще всего находятся на высоте 20 200 километров (12 600 миль) или 20 650 километров (12 830 миль) с периодом обращения 12 часов». [19]
- И геосинхронная орбита (ГСО), и геостационарная орбита (ГСО) являются орбитами вокруг Земли, соответствующими сидерическому периоду вращения Земли . Все геосинхронные и геостационарные орбиты имеют большую полуось 42 164 км (26 199 миль). [20] Все геостационарные орбиты также являются геосинхронными, но не все геосинхронные орбиты являются геостационарными. Геостационарная орбита остается точно над экватором, тогда как геосинхронная орбита может отклоняться на север и юг, чтобы покрыть большую часть поверхности Земли. Обе совершают один полный оборот вокруг Земли за сидерические сутки (относительно звезд, а не Солнца).
- Высокая околоземная орбита : геоцентрические орбиты выше высоты геосинхронной орбиты 35 786 км (22 240 миль ). [19]
Масштабирование в гравитации
Гравитационная постоянная G рассчитывается как:
- (6,6742 ± 0,001) × 10−11 ( кг/м3 ) −1 с − 2 .
Таким образом, константа имеет размерную плотность −1 умножить на −2 . Это соответствует следующим свойствам.
Масштабирование расстояний (включая размеры тел, сохраняя при этом плотности одинаковыми) дает похожие орбиты без масштабирования времени: если, например, расстояния делятся вдвое, массы делятся на 8, силы тяготения на 16, а ускорения гравитации на 2. Следовательно, скорости делятся вдвое, а орбитальные периоды и другие времена перемещения, связанные с гравитацией, остаются прежними. Например, когда объект падает с башни, время, необходимое для падения на землю, остается прежним с масштабной моделью башни на масштабной модели Земли.
Масштабирование расстояний при сохранении масс неизменными (в случае точечных масс или путем корректировки плотностей) дает схожие орбиты; если расстояния умножить на 4, гравитационные силы и ускорения разделить на 16, скорости уменьшить вдвое, а орбитальные периоды умножить на 8.
Если все плотности умножить на 4, орбиты будут одинаковыми; гравитационные силы умножатся на 16, а ускорения на 4, скорости удвоятся, а орбитальные периоды сократятся вдвое.
Когда все плотности умножаются на 4, а все размеры уменьшаются вдвое, орбиты становятся похожими; массы делятся на 2, гравитационные силы одинаковы, гравитационные ускорения удваиваются. Следовательно, скорости становятся одинаковыми, а орбитальные периоды уменьшаются вдвое.
Во всех этих случаях масштабирования, если плотности умножаются на 4, время уменьшается вдвое; если скорости удваиваются, силы умножаются на 16.
Эти свойства иллюстрируются формулой (выведенной из формулы для орбитального периода )
для эллиптической орбиты с большой полуосью a , малого тела вокруг сферического тела с радиусом r и средней плотностью ρ , где T — орбитальный период. См. также третий закон Кеплера .
Патенты
Применение определенных орбит или орбитальных маневров для конкретных полезных целей стало предметом патентов. [21]
Приливная блокировка
Некоторые тела приливно заперты с другими телами, что означает, что одна сторона небесного тела постоянно обращена к своему объекту-хозяину. Это касается систем Земля- Луна и Плутон-Харон.
Смотрите также
- Эфемериды — это свод положений естественных астрономических объектов, а также искусственных спутников на небе в определенный момент времени.
- Свободный дрейф
- розетка Клемперера
- Список орбит
- Орбита Молнии
- Определение орбиты
- Орбитальный космический полет
- Перифокальная система координат
- Полярная орбита
- Радиальная траектория
- Орбита Розетты
- модель VSOP
Ссылки
- ^ "орбита (астрономия)". Encyclopaedia Britannica (Электронная энциклопедия). Архивировано из оригинала 5 мая 2015 года . Получено 28 июля 2008 года .
- ^ "The Space Place :: What's a Barycenter". NASA. Архивировано из оригинала 8 января 2013 года . Получено 26 ноября 2012 года .
- ^ Кун, Коперниканская революция , стр. 238, 246–252.
- ^ Британская энциклопедия , 1968, том. 2, с. 645
- ↑ M Caspar, Kepler (1959, Abelard-Schhuman), на стр. 131–140; A Koyré, The Astronomical Revolution: Copernicus, Kepler, Borelli (1973, Methuen), стр. 277–279
- ^ Джонс, Эндрю. «Законы Кеплера о движении планет». about.com . Архивировано из оригинала 18 ноября 2016 года . Получено 1 июня 2008 года .
- ↑ См. страницы 6–8 в «Трактате о системе мира» Ньютона, архивированном 30 декабря 2016 г. на Wayback Machine (написано в 1685 г., переведено на английский в 1728 г., см. «Начала» Ньютона – предварительная версия ), для получения оригинальной версии этого мысленного эксперимента с «пушечным ядром».
- ^ Карлтон, Тимоти; Го, Ичэн; Мунши, Фера; Треммель, Майкл; Райт, Анна (2021). «Избыток шаровых скоплений в ультрадиффузных галактиках образовался в результате приливного нагрева». Ежемесячные уведомления Королевского астрономического общества . 502 : 398–406. arXiv : 2008.11205 . дои : 10.1093/mnras/stab031 .
- ^ Фицпатрик, Ричард (2 февраля 2006 г.). «Планетные орбиты». Классическая механика – вводный курс . Техасский университет в Остине. Архивировано из оригинала 3 марта 2001 г.
- ^ Луо, Сивэй (22 июня 2020 г.). «Проблема Штурма-Лиувилля для системы двух тел». Journal of Physics Communications . 4 (6): 061001. Bibcode : 2020JPhCo...4f1001L. doi : 10.1088/2399-6528/ab9c30 .
- ↑ Pogge, Richard W.; «Real-World Relativity: The GPS Navigation System» Архивировано 14 ноября 2015 г. на Wayback Machine . Получено 25 января 2008 г.
- ^ Festou, M.; Keller, H. Uwe; Weaver, Harold A. (2004). Кометы II. Издательство Университета Аризоны. стр. 157. ISBN 9780816524501.
- ^ Иорио, Л. (2011). "Возмущенные движения звезд вокруг вращающейся черной дыры в Sgr A* для общей ориентации ее оси вращения". Physical Review D. 84 ( 12): 124001. arXiv : 1107.2916 . Bibcode : 2011PhRvD..84l4001I. doi : 10.1103/PhysRevD.84.124001. S2CID 118305813.
- ^ Рензетти, Г. (2013). «Прецессии орбиты спутника, вызванные октуполярным моментом массы несферического тела, произвольно ориентированного в пространстве». Журнал астрофизики и астрономии . 34 (4): 341–348. Bibcode : 2013JApA...34..341R. doi : 10.1007/s12036-013-9186-4. S2CID 120030309.
- ^ Renzetti, G. (2014). «Орбитальные прецессии спутников, вызванные первым нечетным зональным мультиполем J3 несферического тела, произвольно ориентированного в пространстве». Астрофизика и космическая наука . 352 (2): 493–496. Bibcode : 2014Ap&SS.352..493R. doi : 10.1007/s10509-014-1915-x. S2CID 119537102.
- ^ Ченчинер, Ален; Монтгомери, Ричард (31 октября 2000 г.). «Замечательное периодическое решение задачи трех тел в случае равных масс». arXiv : math/0011268 .
- ^ ab Peterson, Ivars (23 сентября 2013 г.). "Странные орбиты". Science News . Архивировано из оригинала 22 ноября 2015 г. . Получено 21 июля 2017 г. .
- ^ "NASA Safety Standard 1740.14, Guidelines and Assessment Procedures for Limiting Orbital Debris" (PDF) . Управление по безопасности и обеспечению выполнения миссий. 1 августа 1995 г. Архивировано из оригинала (PDF) 15 февраля 2013 г., стр. 37–38 (6-1, 6-2); рисунок 6-1.
- ^ ab "Орбита: Определение". Вспомогательное описание Writer's Guide, 2013. Национальное управление по аэронавтике и исследованию космического пространства (НАСА) Global Change Master Directory. Архивировано из оригинала 11 мая 2013 года . Получено 29 апреля 2013 года .
- ^ Валладо, Дэвид А. (2007). Основы астродинамики и их применение . Хоторн, Калифорния: Microcosm Press. стр. 31.
- ^ Феррейра, Бекки (19 февраля 2015 г.). «Как спутниковые компании патентуют свои орбиты». Motherboard . Vice News. Архивировано из оригинала 18 января 2017 г. . Получено 20 сентября 2018 г. .
Дальнейшее чтение
- Эйбелл, Джордж О.; Моррисон, Дэвид и Вольф, Сидней К. (1987). Исследование Вселенной (Пятое издание). Saunders College Publishing. ISBN 9780030051432.
- Линтон, Кристофер (2004). От Евдокса до Эйнштейна: История математической астрономии. Cambridge University Press. ISBN 978-1-139-45379-0.
- Милани, Андреа; Гронки, Джованни Ф. (2010). Теория определения орбиты . Издательство Кембриджского университета.Обсуждаются новые алгоритмы определения орбит как естественных, так и искусственных небесных тел.
- Свец, Фрэнк; Фовель, Джон; Йоханссон, Бенгт; Кац, Виктор; Беккен, Отто (1995). Учитесь у Мастеров. МАА. ISBN 978-0-88385-703-8.
Внешние ссылки
- CalcTool: Калькулятор орбитального периода планеты. Имеет широкий выбор единиц. Требуется JavaScript.
- Моделирование орбитального движения на Java. Требуется Java.
- Страница NOAA о данных о влиянии на климат содержит (расчетные) данные об изменениях орбиты Земли за последние 50 миллионов лет и на ближайшие 20 миллионов лет.
- Онлайн-построитель орбит. Требуется JavaScript.
- Орбитальная механика (ракетно-космическая техника)
- Орбитальные моделирования Варади, Гиля и Раннегара (2003) дают еще один, немного отличающийся ряд для эксцентриситета земной орбиты, а также ряд для наклонения орбиты. Орбиты других планет также были рассчитаны Ф. Варади; Б. Раннегаром; М. Гилем (2003). "Последовательные уточнения в долгосрочных интеграциях планетарных орбит". The Astrophysical Journal . 592 (1): 620–630. Bibcode :2003ApJ...592..620V. doi : 10.1086/375560 ., но в сети доступны только данные об эксцентриситете Земли и Меркурия.
- Понимание орбит с помощью прямого манипулирования Архивировано 8 ноября 2017 г. в Wayback Machine . Требуются JavaScript и Macromedia
- Меррифилд, Майкл. «Орбиты (включая первую пилотируемую орбиту)». Шестьдесят символов . Брэди Харан для Ноттингемского университета .





























![{\displaystyle {\begin{aligned}{\hat {\mathbf {O} }}&=r{\hat {\mathbf {r} }}\\{\dot {\mathbf {O} }}&={ \frac {\delta r}{\delta t}}{\hat {\mathbf {r} }}+r{\frac {\delta {\hat {\mathbf {r} }}}{\delta t}} = {\dot {r}}{\hat {\mathbf {r} }}+r\left[{\dot {\theta }}{\hat {\boldsymbol {\theta }}}\right]\\{ \ddot {\mathbf {O} }}&=\left[{\ddot {r}}{\hat {\mathbf {r} }}+{\dot {r}}{\dot {\theta }}{\hat {\boldsymbol {\theta }}}\right]+\left[{\dot {r}}{\dot {\theta }}{\hat { \boldsymbol {\theta }}}+r{\ddot {\theta }}{\hat {\boldsymbol {\theta }}}-r{\dot {\theta }}^{2}{\hat {\mathbf {r} }}\right]\\&=\left[{\ddot {r}}-r{\dot {\theta }}^{2}\right]{\hat {\mathbf {r} }} +\left[r{\ddot {\theta }}+2{\dot {r}}{\dot {\theta }}\right]{\hat {\boldsymbol {\theta }}}\end{выровнено}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d92049db70580d670e5dd37a305c3ebd3073f2b2)






























