Гипербола


В математике гипербола — это тип гладкой кривой, лежащей в плоскости , определяемой ее геометрическими свойствами или уравнениями , для которых она является множеством решений. Гипербола состоит из двух частей, называемых связными компонентами или ветвями, которые являются зеркальными отображениями друг друга и напоминают две бесконечные дуги . Гипербола — это один из трех видов конического сечения , образованного пересечением плоскости и двойного конуса . (Другие конические сечения — это парабола и эллипс . Окружность — это частный случай эллипса.) Если плоскость пересекает обе половины двойного конуса, но не проходит через вершины конусов, то коническое сечение является гиперболой.
Помимо того, что гипербола является коническим сечением, она может возникать как геометрическое место точек, разность расстояний которых до двух фиксированных фокусов постоянна, как кривая для каждой точки, лучи которой до двух фиксированных фокусов являются отражениями относительно касательной в этой точке, или как решение некоторых двумерных квадратных уравнений, таких как соотношение обратных величин [1]. В практических приложениях гипербола может возникать как путь, по которому падает тень от кончика гномона солнечных часов , форма открытой орбиты , например, орбиты небесного объекта, превышающего скорость убегания ближайшего гравитационного тела, или траектория рассеяния субатомной частицы и т. д.
Каждая ветвь гиперболы имеет два плеча, которые становятся более прямыми (меньшей кривизной) дальше от центра гиперболы. Диагонально противоположные плечи, по одному от каждой ветви, стремятся в пределе к общей линии, называемой асимптотой этих двух плеч. Таким образом, есть две асимптоты, пересечение которых находится в центре симметрии гиперболы , который можно рассматривать как точку зеркала, относительно которой каждая ветвь отражается, образуя другую ветвь. В случае кривой асимптоты являются двумя осями координат . [1]
Гиперболы разделяют многие аналитические свойства эллипсов, такие как эксцентриситет , фокус и директриса . Обычно соответствие можно установить всего лишь с помощью изменения знака в некотором термине. Многие другие математические объекты берут свое начало в гиперболе, например, гиперболические параболоиды (седловые поверхности), гиперболоиды («мусорные корзины»), гиперболическая геометрия ( знаменитая неевклидова геометрия Лобачевского ), гиперболические функции (sinh, cosh, tanh и т. д.) и гировекторные пространства (геометрия, предложенная для использования как в теории относительности , так и в квантовой механике , которая не является евклидовой ).
Этимология и история
Слово «гипербола» происходит от греческого ὑπερβολή , что означает «опрокинутый» или «чрезмерный», от которого также происходит английский термин hyperbole . Гиперболы были открыты Менехмом в его исследованиях задачи удвоения куба , но затем были названы сечениями тупых конусов. [2] Термин гипербола, как полагают, был придуман Аполлонием Пергским ( ок. 262 – ок. 190 до н. э. ) в его окончательном труде о конических сечениях , «Коники» . [3] Названия двух других общих конических сечений, эллипс и парабола , происходят от соответствующих греческих слов для «недостаточный» и «примененный»; все три названия заимствованы из более ранней пифагорейской терминологии, которая относилась к сравнению стороны прямоугольников фиксированной площади с заданным отрезком прямой. Прямоугольник может быть «применен» к сегменту (то есть иметь равную длину), быть короче сегмента или превышать его. [4]
Определения
Как геометрическое место точек


Гиперболу можно геометрически определить как множество точек ( геометрическое место точек ) на евклидовой плоскости:
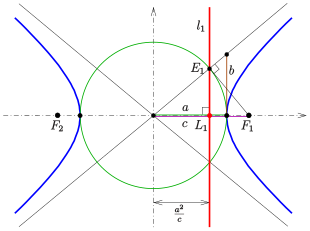
Середина отрезка, соединяющего фокусы, называется центром гиперболы. [6] Прямая, проходящая через фокусы, называется большой осью . Она содержит вершины , которые имеют расстояние до центра. Расстояние фокусов до центра называется фокусным расстоянием или линейным эксцентриситетом . Частное — это эксцентриситет .
Уравнение можно рассматривать по-другому (см. схему):
Если — окружность с серединой и радиусом , то расстояние от точки правой ветви до окружности равно расстоянию до фокуса : называется круговой директрисой (относительно фокуса ) гиперболы. [7] [8] Для того чтобы получить левую ветвь гиперболы, нужно использовать круговую директрису, связанную с . Это свойство не следует путать с определением гиперболы с помощью директрисы (линии) ниже.
Гипербола с уравнениему = А / х

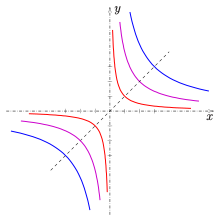
Если систему координат xy повернуть вокруг начала координат на угол и задать новые координаты , то .
Прямоугольная гипербола ( полуоси которой равны) имеет новое уравнение . Решение для дает
Таким образом, в системе координат xy график функции с уравнением представляет собой прямоугольную гиперболу целиком в первом и третьем квадрантах с
- оси координат как асимптоты ,
- линия как большая ось ,
- центр и полуось
- вершины
- полуширокая прямая кишка и радиус кривизны в вершинах
- линейный эксцентриситет и эксцентриситет
- касательная в точке
Вращение исходной гиперболы на приводит к прямоугольной гиперболе, полностью находящейся во втором и четвертом квадрантах, с теми же асимптотами, центром, прямой полушириной, радиусом кривизны в вершинах, линейным эксцентриситетом и эксцентриситетом, что и в случае вращения, с уравнением
- полуоси
- линия как большая ось,
- вершины
Сдвиг гиперболы с уравнением так, чтобы новый центр был , дает новое уравнение и новые асимптоты и . Параметры формы остаются неизменными.
По свойству директрисы


Две линии, удаленные от центра и параллельные малой оси, называются директрисами гиперболы (см. рисунок).
Для произвольной точки гиперболы частное от деления расстояния до одного фокуса и до соответствующей ему директрисы (см. рисунок) равно эксцентриситету: Доказательство для пары следует из того, что и удовлетворяют уравнению Второй случай доказывается аналогично.

Обратное утверждение также верно и может быть использовано для определения гиперболы (аналогично определению параболы):
Для любой точки (фокуса), любой прямой (директрисы), не проходящей через множество точек (геометрическое место точек), для которого частное расстояний до точки и до прямой равно, есть гипербола.
(Выбор дает параболу , а если — эллипс . )
Доказательство
Пусть и предположим, что это точка на кривой. Директриса имеет уравнение . При этом отношение дает уравнения
- и
Подстановка дает Это уравнение эллипса ( ) или параболы ( ) или гиперболы ( ). Все эти невырожденные коники имеют, как общее, начало координат в качестве вершины (см. диаграмму).
Если ввести новые параметры так, чтобы , и тогда уравнение выше становится уравнением гиперболы с центром , осью x в качестве большой оси и большой/малой полуосью .
Построение директрисы
Поскольку точка директрисы (см. схему) и фокус обратны по отношению к инверсии окружности в окружности (на схеме зелёный). Следовательно, точка может быть построена с помощью теоремы Фалеса (на схеме не показана). Директриса — это перпендикуляр к прямой, проходящей через точку .
Альтернативное построение : Расчет показывает, что точка является пересечением асимптоты с ее перпендикуляром (см. диаграмму).
Как плоское сечение конуса

Пересечение прямого двойного конуса плоскостью, не проходящей через вершину с наклоном, большим, чем наклон прямых на конусе, является гиперболой (см. диаграмму: красная кривая). Для доказательства определяющего свойства гиперболы (см. выше) используются две сферы Данделена , которые являются сферами, касающимися конуса по окружностям , и пересекающая (гиперболическая) плоскость в точках и . Оказывается: являются фокусами гиперболы.
- Пусть – произвольная точка кривой пересечения.
- Образующая конуса, содержащая окружность, пересекает окружность в точке и окружность в точке .
- Отрезки и касательны к сфере и, следовательно, имеют одинаковую длину.
- Отрезки и касательны к сфере и, следовательно, имеют одинаковую длину.
- Результат: не зависит от точки гиперболы , потому что независимо от того, где находится точка, она должна находиться на окружностях , и отрезок должен пересекать вершину. Поэтому, когда точка движется вдоль красной кривой (гиперболы), отрезок просто вращается вокруг вершины, не меняя своей длины.
Конструкция штифта и струны

Определение гиперболы по ее фокусам и ее окружностям-директрисам (см. выше) можно использовать для построения ее дуги с помощью булавок, нити и линейки: [9]
- Выберите фокусы , вершины и одну из окружностей-директрис , например (окружность с радиусом )
- Линейка закреплена в точке, вокруг которой она может свободно вращаться . Точка отмечена на расстоянии .
- Подготавливается строка длиной .
- Один конец нити прикрепляется булавкой к точке на линейке, другой конец прикрепляется булавкой к точке .
- Возьмите ручку и прижмите нить к краю линейки.
- Вращение линейки побуждает ручку рисовать дугу правой ветви гиперболы, поскольку (см. определение гиперболы по круговым директрисам ).
Генерация гиперболы Штейнера


Следующий метод построения отдельных точек гиперболы основан на построении Штейнера невырожденного конического сечения :
Для генерации точек гиперболы используются пучки в вершинах . Пусть будет точкой гиперболы и . Отрезок прямой делится на n равноотстоящих сегментов, и это деление проецируется параллельно диагонали как направлению на отрезок прямой (см. диаграмму). Параллельная проекция является частью проективного отображения между пучками в и , необходимого для этого. Точки пересечения любых двух связанных прямых и являются точками однозначно определенной гиперболы.
Замечания:
- Подразделение можно было бы расширить за пределы точек и для того, чтобы получить больше точек, но определение точек пересечения стало бы более неточным. Лучшей идеей является расширение уже построенных симметрией точек (см. анимацию).
- Поколение Штейнера существует также для эллипсов и парабол.
- Метод Штейнера иногда называют методом параллелограмма, поскольку вместо вершин можно использовать другие точки, что дает параллелограмм вместо прямоугольника.
Вписанные углы гиперболу = а /( х − b ) + си 3-точечная форма

Гипербола с уравнением однозначно определяется тремя точками с различными x - и y -координатами. Простой способ определения параметров формы использует теорему о вписанном угле для гипербол:
Аналогично теореме о вписанном угле для окружностей получаем
Теорема о вписанном угле для гипербол [10] [11] — Для четырех точек (см. диаграмму) справедливо следующее утверждение:
Четыре точки находятся на гиперболе с уравнением тогда и только тогда, когда углы при и равны в смысле измерения выше. Это означает, что если
Доказательство можно получить путем прямого вычисления. Если точки находятся на гиперболе, можно предположить, что уравнение гиперболы имеет вид .
Следствием теоремы о вписанном угле для гипербол является
Уравнение гиперболы в трехточечной форме — Уравнение гиперболы, определенное по трем точкам, является решением уравнения для .
Как аффинный образ единичной гиперболых 2 − у 2 = 1

Другое определение гиперболы использует аффинные преобразования :
Параметрическое представление
Аффинное преобразование евклидовой плоскости имеет вид , где — регулярная матрица (ее определитель не равен 0), а — произвольный вектор. Если — векторы-столбцы матрицы , то единичная гипербола отображается на гиперболу
— центр, точка гиперболы и касательный вектор в этой точке.
Вершины
В общем случае векторы не перпендикулярны. Это означает, что в общем случае они не являются вершинами гиперболы. Но указывают на направления асимптот. Касательный вектор в точке равен Поскольку в вершине касательная перпендикулярна большой оси гиперболы, из уравнения получаем параметр вершины и, следовательно, из чего следует
Были использованы формулы , , и .
Две вершины гиперболы — это
Неявное представление
Решая параметрическое представление для по правилу Крамера и используя , получаем неявное представление
Гипербола в космосе
Определение гиперболы в этом разделе дает параметрическое представление произвольной гиперболы, даже в пространстве, если допустить, что являются векторами в пространстве.
Как аффинное изображение гиперболыу = 1/ х

Поскольку единичная гипербола аффинно эквивалентна гиперболе , произвольную гиперболу можно рассматривать как аффинное изображение (см. предыдущий раздел) гиперболы :
— центр гиперболы, векторы имеют направления асимптот и — точка гиперболы. Касательный вектор равен В вершине касательная перпендикулярна большой оси. Следовательно , а параметр вершины равен
эквивалентно и являются вершинами гиперболы.
Следующие свойства гиперболы легко доказываются с помощью представления гиперболы, введенного в этом разделе.
Строительство касательной

Касательный вектор можно переписать с помощью факторизации: Это означает, что
Это свойство дает возможность построить касательную в точке гиперболы.
Это свойство гиперболы является аффинной версией теоремы Паскаля о трехточечном вырождении . [12]
- Площадь серого параллелограмма
Площадь серого параллелограмма на приведенной выше диаграмме равна и, следовательно, не зависит от точки . Последнее уравнение следует из расчета для случая, где есть вершина и гипербола в ее канонической форме
Точечная конструкция

Для гиперболы с параметрическим представлением (для простоты центром является начало координат) справедливо следующее:
коллинеарны с центром гиперболы (см. диаграмму).
Простое доказательство является следствием уравнения .
Это свойство дает возможность построить точки гиперболы, если заданы асимптоты и одна точка.
Это свойство гиперболы является аффинной версией теоремы Паскаля о 4-точечном вырождении . [13]
Треугольник касательных и асимптот

Для простоты центр гиперболы может быть началом координат, а векторы иметь одинаковую длину. Если последнее предположение не выполняется, можно сначала применить преобразование параметров (см. выше), чтобы сделать предположение верным. Следовательно , вершины охватывают малую ось и получается и .
Для точек пересечения касательной в точке с асимптотами получаем точки Площадь треугольника можно вычислить с помощью определителя 2 × 2: (см. правила для определителей ). — площадь ромба, порожденного . Площадь ромба равна половине произведения его диагоналей. Диагонали являются полуосями гиперболы. Следовательно:
Возвратно-поступательное движение круга
Возвратно -поступательное движение окружности B в окружности C всегда дает коническое сечение , такое как гипербола. Процесс "возвратно-поступательного движения в окружности C " состоит в замене каждой линии и точки в геометрической фигуре на их соответствующие полюс и поляру соответственно. Полюс линии является инверсией ее ближайшей точки к окружности C , тогда как полярой точки является обратное, а именно, линия, ближайшая точка которой к C является инверсией точки.
Эксцентриситет конического сечения, полученного возвратно-поступательным движением, равен отношению расстояний между центрами двух окружностей к радиусу r возвратно-поступательной окружности C. Если B и C представляют собой точки в центрах соответствующих окружностей, то
Поскольку эксцентриситет гиперболы всегда больше единицы, центр B должен лежать вне обратной окружности C.
Это определение подразумевает, что гипербола является как геометрическим местом полюсов касательных линий к окружности B , так и огибающей полярных линий точек на B. Наоборот, окружность B является огибающей поляр точек на гиперболе и геометрическим местом полюсов касательных линий к гиперболе. Две касательные линии к B не имеют (конечных) полюсов, поскольку они проходят через центр C окружности взаимного перемещения C ; поляры соответствующих точек касания на B являются асимптотами гиперболы. Две ветви гиперболы соответствуют двум частям окружности B , которые разделены этими точками касания.
Квадратное уравнение
Гиперболу можно также определить как уравнение второй степени в декартовых координатах на плоскости ,
при условии, что константы и удовлетворяют условию детерминанта
Этот определитель принято называть дискриминантом конического сечения. [14]
Частный случай гиперболы — вырожденная гипербола, состоящая из двух пересекающихся прямых, — возникает, когда другой определитель равен нулю:
Этот определитель иногда называют дискриминантом конического сечения. [15]
Коэффициенты общего уравнения можно получить из известных координат центра большой полуоси , малой полуоси и угла поворота (угол между положительной горизонтальной осью и большой осью гиперболы) с помощью формул:
Эти выражения можно вывести из канонического уравнения
путем переноса и поворота координат :
Учитывая приведенную выше общую параметризацию гиперболы в декартовых координатах, эксцентриситет можно найти с помощью формулы в Коническом сечении#Эксцентриситет через коэффициенты .
Центр гиперболы можно определить по формулам
В новых координатах определяющее уравнение гиперболы можно записать
Главные оси гиперболы образуют угол с положительной осью, который определяется выражением
Поворот осей координат таким образом, чтобы ось - совпадала с поперечной осью, приводит уравнение к каноническому виду
Большая и малая полуоси определяются уравнениями
где и - корни квадратного уравнения
Для сравнения, соответствующее уравнение для вырожденной гиперболы (состоящей из двух пересекающихся прямых) имеет вид
Касательная к данной точке гиперболы определяется уравнением
где и определяются как
Нормаль к гиперболе в той же точке задается уравнением
Нормальная линия перпендикулярна касательной, и обе проходят через одну и ту же точку.
Из уравнения
левый фокус — это , а правый фокус — это , где — эксцентриситет. Обозначим расстояния от точки до левого и правого фокусов как и Для точки на правой ветви,
и для точки на левой ветви,
Это можно доказать следующим образом:
Если — точка на гиперболе, то расстояние до левого фокуса равно
До правой фокальной точки расстояние равно
Если точка находится на правой ветви гиперболы, то и
Вычитая эти уравнения, получаем
Если — точка на левой ветви гиперболы, то и
Вычитая эти уравнения, получаем
В декартовых координатах
Уравнение
Если ввести декартовы координаты таким образом, что начало координат является центром гиперболы, а ось x является большой осью, то гипербола называется раскрывающейся в направлении восток-запад и
- фокусы — это точки , [6]
- вершины . [ 6 ]
Для произвольной точки расстояние до фокуса равно , а до второго фокуса . Следовательно, точка находится на гиперболе, если выполняется следующее условие: Извлеките квадратные корни с помощью подходящих возведений в квадрат и используйте соотношение для получения уравнения гиперболы:
Это уравнение называется канонической формой гиперболы, поскольку любая гипербола, независимо от ее ориентации относительно декартовых осей и независимо от расположения ее центра, может быть преобразована к этой форме заменой переменных, что даст гиперболу, конгруэнтную исходной (см. ниже).
Оси симметрии или главные оси — это поперечная ось (содержащая отрезок длиной 2a с концами в вершинах) и сопряженная ось (содержащая отрезок длиной 2b , перпендикулярный поперечной оси, со средней точкой в центре гиперболы). [6] В отличие от эллипса, гипербола имеет только две вершины: . Две точки на сопряженных осях не находятся на гиперболе.
Из уравнения следует, что гипербола симметрична относительно обеих осей координат и, следовательно, симметрична относительно начала координат.
Эксцентриситет
Для гиперболы в приведенной выше канонической форме эксцентриситет определяется выражением
Две гиперболы геометрически подобны друг другу, то есть имеют одинаковую форму, так что одну можно преобразовать в другую с помощью жестких движений влево и вправо , вращения , зеркального отображения и масштабирования (увеличения) — тогда и только тогда, когда они имеют одинаковый эксцентриситет.
Асимптоты


Решая уравнение (выше) гиперболы для получаем Из этого следует, что гипербола приближается к двум линиям при больших значениях . Эти две линии пересекаются в центре (начале координат) и называются асимптотами гиперболы [16]
С помощью второго рисунка можно увидеть, что
- Перпендикулярное расстояние от фокуса до любой асимптоты равно (малой полуоси).
Из нормальной формы Гессе асимптот и уравнения гиперболы получаем: [17]
- Произведение расстояний от точки на гиперболе до обеих асимптот является константой , которую также можно записать через эксцентриситет e как
Из уравнения гиперболы (выше) можно вывести:
- Произведение наклонов линий, проведенных из точки P к двум вершинам, является константой
Кроме того, из (2) выше можно показать, что [17]
- Произведение расстояний от точки гиперболы до асимптот вдоль прямых, параллельных асимптотам, есть константа
Полуширокая прямая кишка
Длина хорды, проходящей через один из фокусов, перпендикулярной большой оси гиперболы, называется latus rectum . Одна ее половина — это semi-latus rectum . Расчет показывает, что semi-latus rectum можно также рассматривать как радиус кривизны в вершинах.
Тангенс
Самый простой способ определить уравнение касательной в точке — это неявно продифференцировать уравнение гиперболы. Обозначая dy/dx как y′ , это дает Относительно уравнение касательной в точке имеет вид
Конкретная касательная линия отличает гиперболу от других конических сечений. [18] Пусть f будет расстоянием от вершины V (как на гиперболе, так и на ее оси через два фокуса) до ближайшего фокуса. Тогда расстояние по линии, перпендикулярной этой оси, от этого фокуса до точки P на гиперболе больше 2 f . Касательная к гиперболе в точке P пересекает эту ось в точке Q под углом ∠PQV больше 45°.
Прямоугольная гипербола
В случае гипербола называется прямоугольной (или равносторонней ), так как ее асимптоты пересекаются под прямым углом. Для этого случая линейный эксцентриситет равен , эксцентриситет и полуширота прямая . График уравнения представляет собой прямоугольную гиперболу.
Параметрическое представление с гиперболическим синусом/косинусом
Используя функции гиперболического синуса и косинуса , можно получить параметрическое представление гиперболы , которое аналогично параметрическому представлению эллипса: которое удовлетворяет декартову уравнению, поскольку
Дополнительные параметрические представления приведены в разделе «Параметрические уравнения» ниже.

Сопряженная гипербола
Обменяйте и получите уравнение сопряженной гиперболы (см. диаграмму): также записанное как
Гипербола и ее сопряженная могут иметь диаметры, которые являются сопряженными . В теории специальной теории относительности такие диаметры могут представлять оси времени и пространства, где одна гипербола представляет события на заданном пространственном расстоянии от центра , а другая представляет события на соответствующем временном расстоянии от центра.
В полярных координатах

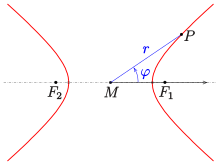

Происхождение в центре внимания
Полярные координаты, наиболее часто используемые для гиперболы, определяются относительно декартовой системы координат, которая имеет начало в фокусе , а ее ось x направлена к началу «канонической системы координат», как показано на первой диаграмме.
В этом случае угол называется истинной аномалией .
Относительно этой системы координат имеем, что
и
Начало в центре
С полярными координатами относительно «канонической системы координат» (см. вторую диаграмму) имеем, что
Для правой ветви гиперболы диапазон равен
Эксцентриситет
При использовании полярных координат эксцентриситет гиперболы можно выразить как где — предел угловой координаты. По мере приближения к этому пределу r стремится к бесконечности, а знаменатель в любом из приведенных выше уравнений стремится к нулю, следовательно: [19] : 219
Параметрические уравнения
Гиперболу с уравнением можно описать несколькими параметрическими уравнениями:
- Через гиперболические тригонометрические функции
- Как рациональное представление
- Через круговые тригонометрические функции
- С наклоном касательной в качестве параметра:Параметрическое представление, использующее наклон касательной в точке гиперболы, можно получить аналогично случаю эллипса: Заменим в случае эллипса на и используем формулы для гиперболических функций . Получаем Здесь — верхняя, а — нижняя половины гиперболы. Точки с вертикальными касательными (вершины ) представлением не охватываются.Уравнение касательной в точке имеет вид Это описание касательных гиперболы является важным инструментом для определения ортооптики гиперболы .
Гиперболические функции

Так же, как тригонометрические функции определяются в терминах единичной окружности , так и гиперболические функции определяются в терминах единичной гиперболы , как показано на этой диаграмме. В единичной окружности угол (в радианах) равен удвоенной площади кругового сектора , который этот угол охватывает. Аналогичный гиперболический угол также определяется как удвоенная площадь гиперболического сектора .
Пусть будет удвоенной площадью между осью и лучом, проходящим через начало координат, пересекающим единичную гиперболу, и определите как координаты точки пересечения. Тогда площадь гиперболического сектора равна площади треугольника за вычетом криволинейной области за вершиной в : что упрощается до площади гиперболического косинуса Решение для дает экспоненциальную форму гиперболического косинуса: Из одного получаем и его обратную площадь гиперболического синуса : Другие гиперболические функции определяются в соответствии с гиперболическим косинусом и гиперболическим синусом, например
Характеристики
Свойство отражения

Касательная в точке делит угол между прямыми пополам. Это называется оптическим свойством или свойством отражения гиперболы. [20]
- Доказательство
Пусть будет точкой на прямой с расстоянием до фокуса (см. диаграмму, — большая полуось гиперболы). Прямая — биссектриса угла между прямыми . Чтобы доказать, что — касательная в точке , проверяют, что любая точка на прямой, отличная от , не может быть на гиперболе. Следовательно, имеет только общую точку с гиперболой и, следовательно, является касательной в точке .
Из диаграммы и неравенства треугольника следует, что выполняется, что означает: . Но если — точка гиперболы, то разность должна быть .
Средние точки параллельных хорд


Середины параллельных хорд гиперболы лежат на прямой, проходящей через центр (см. рисунок).
Точки любой хорды могут лежать на разных ветвях гиперболы.
Доказательство свойства для средних точек лучше всего провести для гиперболы . Поскольку любая гипербола является аффинным образом гиперболы (см. раздел ниже), а аффинное преобразование сохраняет параллельность и средние точки отрезков, свойство справедливо для всех гипербол:
Для двух точек гиперболы
- середина аккорда - это
- наклон хорды равен
Для параллельных хорд наклон постоянен, а середины параллельных хорд лежат на линии
Следствие: для любой пары точек хорды существует косое отражение с осью (множеством неподвижных точек), проходящей через центр гиперболы, которое меняет точки и оставляет гиперболу (в целом) неподвижной. Косое отражение является обобщением обычного отражения относительно прямой , где все пары точка-изображение находятся на прямой, перпендикулярной .
Поскольку косое отражение оставляет гиперболу неподвижной, пара асимптот также неподвижна. Следовательно, середина хорды делит соответствующий отрезок прямой между асимптотами пополам. Это означает, что . Это свойство можно использовать для построения дальнейших точек гиперболы, если заданы точка и асимптоты.
Если хорда вырождается в касательную , то точка касания делит отрезок между асимптотами пополам.
Ортогональные касательные – ортоптические

Для гиперболы точки пересечения ортогональных касательных лежат на окружности .
Эта окружность называется ортоптической данной гиперболы.
Касательные могут принадлежать точкам на разных ветвях гиперболы.
В случае нет пар ортогональных касательных.
Полюсно-полярное соотношение для гиперболы

Любая гипербола может быть описана в подходящей системе координат уравнением . Уравнение касательной в точке гиперболы имеет вид Если допустить, что точка является произвольной точкой, отличной от начала координат, то
- точка отображается на линию , а не через центр гиперболы.
Это отношение между точками и линиями является биекцией .
Обратная функция отображает
- линия на точку и
- линия на точку
Такое отношение между точками и прямыми, образованное коникой, называется отношением полюс-полярность или просто полярностью . Полюс — это точка, поляра — линия. См. Полюс и поляра .
Расчетным путем проверяются следующие свойства полюсно-полярного отношения гиперболы:
- Для точки (полюса) гиперболы полярой является касательная в этой точке (см. рисунок: ).
- Для полюса вне гиперболы точки пересечения его поляры с гиперболой являются точками касания двух проходящих касательных (см. рисунок: ).
- Для точки внутри гиперболы поляра не имеет общих точек с гиперболой (см. диаграмму: ).
Замечания:
- Точка пересечения двух поляр (например: ) является полюсом линии, проходящей через их полюса (здесь: ).
- Фокус и соответственно, а директрисы и соответственно принадлежат парам полюса и поляры.
Полюсно-полярные соотношения существуют также для эллипсов и парабол.
Другие свойства
- Конкурентными являются : (1) окружность, проходящая через фокусы гиперболы с центром в центре гиперболы; (2) любая из прямых, которые касаются гиперболы в вершинах; и (3) любая из асимптот гиперболы. [21] [22]
- Следующие точки также являются совпадающими: (1) окружность с центром в центре гиперболы, проходящая через ее вершины; (2) любая из директрис; и (3) любая из асимптот. [22]
- Поскольку и поперечная ось, и сопряженная ось являются осями симметрии, то группа симметрии гиперболы — это четверная группа Клейна .
- Прямоугольные гиперболы xy = const допускают групповые действия посредством отображений сжатия , которые имеют гиперболы в качестве инвариантных множеств .
Длина дуги
Длина дуги гиперболы не имеет элементарного выражения . Верхняя половина гиперболы может быть параметризована как
Тогда интеграл, задающий длину дуги от до, можно вычислить как:
После применения подстановки это можно также представить с помощью неполного эллиптического интеграла второго рода с параметром :
Используя только действительные числа, это становится [23]
где — неполный эллиптический интеграл первого рода с параметром , а — функция Гудермана .
Производные кривые

Несколько других кривых могут быть получены из гиперболы путем инверсии , так называемые обратные кривые гиперболы. Если центр инверсии выбран как собственный центр гиперболы, обратная кривая является лемнискатой Бернулли ; лемниската также является огибающей окружностей с центром на прямоугольной гиперболе и проходящей через начало координат. Если центр инверсии выбран в фокусе или вершине гиперболы, полученные обратные кривые являются улиткой или строфоидом соответственно .
Эллиптические координаты
Семейство конфокальных гипербол является основой системы эллиптических координат в двух измерениях. Эти гиперболы описываются уравнением
где фокусы расположены на расстоянии c от начала координат на оси x , и где θ — угол асимптот с осью x . Каждая гипербола в этом семействе ортогональна каждому эллипсу, который разделяет те же фокусы. Эту ортогональность можно показать с помощью конформной карты декартовой системы координат w = z + 1/ z , где z = x + iy — исходные декартовы координаты, а w = u + iv — координаты после преобразования.
Другие ортогональные двумерные системы координат, включающие гиперболы, могут быть получены другими конформными отображениями. Например, отображение w = z 2 преобразует декартову систему координат в два семейства ортогональных гипербол.
Анализ конического сечения гиперболического вида окружностей

В качестве изображений окружностей получаются окружность (пурпурная), эллипсы, гиперболы и прямые. Частный случай параболы в этом примере не появляется.
(Если бы центр O находился на сфере, все изображения окружностей были бы окружностями или прямыми; см. стереографическую проекцию ).
Помимо предоставления единообразного описания окружностей, эллипсов, парабол и гипербол, конические сечения также можно понимать как естественную модель геометрии перспективы в случае, когда рассматриваемая сцена состоит из окружностей или, в более общем смысле, эллипса. Зрителем обычно является камера или человеческий глаз, а изображение сцены — центральная проекция на плоскость изображения, то есть все проекционные лучи проходят через фиксированную точку O , центр. Плоскость линзы — это плоскость, параллельная плоскости изображения в линзе O.
Изображение круга c есть
- окружность , если окружность c находится в особом положении, например, параллельно плоскости изображения и др. (см. стереографическую проекцию) ,
- эллипс , если c не имеет общей точки с плоскостью линзы,
- парабола , если c имеет одну общую точку с плоскостью линзы и
- гипербола , если c имеет две общие точки с плоскостью линзы .
(Особые положения, в которых плоскость окружности содержит точку O, опущены.)
Эти результаты можно понять, если признать, что процесс проецирования можно рассматривать в два этапа: 1) окружность c и точка O образуют конус, который 2) пересекается плоскостью изображения, чтобы создать изображение.
Человек видит гиперболу всякий раз, когда видит часть круга, вырезанного плоскостью линзы. Неспособность увидеть большую часть ветвей видимой ветви, в сочетании с полным отсутствием второй ветви, делает практически невозможным для зрительной системы человека распознавание связи с гиперболами.
Приложения


Солнечные часы
Гиперболы можно увидеть во многих солнечных часах . В любой день солнце вращается по кругу на небесной сфере , и его лучи, попадая на точку на солнечных часах, очерчивают конус света. Пересечение этого конуса с горизонтальной плоскостью земли образует коническое сечение. На большинстве населенных широт и в большинство времен года это коническое сечение является гиперболой. С практической точки зрения, тень от кончика шеста очерчивает гиперболу на земле в течение дня (этот путь называется линией склонения ). Форма этой гиперболы меняется в зависимости от географической широты и времени года, поскольку эти факторы влияют на конус солнечных лучей относительно горизонта. Совокупность таких гипербол в течение целого года в данном месте греки называли пелекиноном , поскольку она напоминает двухлезвийный топор.
Мультилатерация
Гипербола является основой для решения задач мультилатерации , задачи определения местоположения точки по разнице расстояний до заданных точек — или, что эквивалентно, по разнице во времени прибытия синхронизированных сигналов между точкой и заданными точками. Такие задачи важны в навигации, особенно на воде; судно может определить свое местоположение по разнице во времени прибытия сигналов от передатчиков LORAN или GPS . И наоборот, радиомаяк или любой передатчик можно определить, сравнив время прибытия его сигналов на две отдельные приемные станции; такие методы могут использоваться для отслеживания объектов и людей. В частности, множество возможных положений точки, которая имеет разницу в расстоянии 2 a от двух заданных точек, представляет собой гиперболу с разделением вершин 2 a, фокусами которой являются две заданные точки.
Путь, пройденный частицей
Путь, по которому движется любая частица в классической задаче Кеплера, представляет собой коническое сечение . В частности, если полная энергия E частицы больше нуля (то есть, если частица не связана), то путь такой частицы представляет собой гиперболу. Это свойство полезно при изучении атомных и субатомных сил путем рассеяния частиц высокой энергии; например, эксперимент Резерфорда продемонстрировал существование атомного ядра путем изучения рассеяния альфа-частиц на атомах золота . Если игнорировать ядерные взаимодействия на близком расстоянии, то атомное ядро и альфа-частица взаимодействуют только посредством отталкивающей кулоновской силы , которая удовлетворяет требованию закона обратных квадратов для задачи Кеплера. [24]
Уравнение Кортевега–де Фриза
Гиперболическая тригонометрическая функция является одним из решений уравнения Кортевега–де Фриза , описывающего движение солитонной волны в канале.
Трисекция угла

Как впервые показал Аполлоний Пергский , гиперболу можно использовать для трисекции любого угла , хорошо изученная задача геометрии. Для заданного угла сначала нарисуйте окружность с центром в его вершине O , которая пересекает стороны угла в точках A и B. Затем нарисуйте отрезок прямой с конечными точками A и B и его серединный перпендикуляр . Постройте гиперболу с эксцентриситетом e = 2 с директрисой и B в качестве фокуса. Пусть P будет пересечением (верхним) гиперболы с окружностью. Угол POB трисектсирует угол AOB .
Чтобы доказать это, отразим отрезок OP относительно прямой, получив точку P' как изображение P. Отрезок AP' имеет ту же длину, что и отрезок BP из-за отражения, в то время как отрезок PP' имеет ту же длину, что и отрезок BP из-за эксцентриситета гиперболы. [25] Поскольку OA , OP' , OP и OB являются радиусами одной и той же окружности (и, следовательно, имеют одинаковую длину), треугольники OAP' , OPP' и OPB все конгруэнтны. Следовательно, угол был разделен на три части, так как 3× POB = AOB . [26]
Граница эффективного портфеля
В теории портфеля геометрическое место эффективных портфелей по средней дисперсии (называемое эффективной границей) представляет собой верхнюю половину ветви гиперболы, открывающейся на восток, нарисованной с использованием стандартного отклонения доходности портфеля, нанесенного по горизонтали, и его ожидаемого значения, нанесенного по вертикали; согласно этой теории, все рациональные инвесторы выбрали бы портфель, характеризующийся некоторой точкой на этом местоположении.
Биохимия
В биохимии и фармакологии уравнения Хилла и Хилла-Ленгмюра соответственно описывают биологические реакции и образование комплексов белок-лиганд как функции концентрации лиганда. Они оба являются прямоугольными гиперболами.
Гиперболы как плоские сечения квадрик
Гиперболы появляются как плоские сечения следующих квадрик :
- Эллиптический конус
- Гиперболический цилиндр
- Гиперболический параболоид
- Однополостный гиперболоид
- Двуполостный гиперболоид
- Эллиптический конус
- Гиперболический цилиндр
- Гиперболический параболоид
- Однополостный гиперболоид
- Двуполостный гиперболоид
Смотрите также
Другие конические сечения
Другие похожие темы
- Эллиптические координаты — ортогональная система координат, основанная на семействах эллипсов и гипербол.
- Гиперболический рост
- Гиперболическое уравнение в частных производных
- Гиперболический сектор
- Гиперболоидная структура
- Гиперболическая траектория
- Гиперболоид
- Мультилатерация
- Вращение осей
- Перевод осей
- Единичная гипербола
Примечания
- ^ ab Oakley 1944, стр. 17.
- ↑ Хит, сэр Томас Литтл (1896), «Глава I. Открытие конических сечений. Менехм», Аполлоний Пергский: Трактат о конических сечениях с введениями, включая эссе о более ранней истории предмета, Cambridge University Press, стр. xvii–xxx.
- ^ Бойер, Карл Б.; Мерцбах, Ута К. (2011), История математики, Wiley, стр. 73, ISBN 9780470630563Именно
Аполлоний (возможно, следуя предложению Архимеда) ввел названия «эллипс» и «гипербола» в связи с этими кривыми.
- ↑ Ивс, Говард (1963), Обзор геометрии (т. 1) , Аллин и Бэкон, стр. 30–31
- ^ Проттер и Морри 1970, стр. 308–310.
- ^ abcd Проттер и Морри 1970, стр. 310.
- ^ Апостол, Том М.; Мнацаканян, Мамикон А. (2012), Новые горизонты в геометрии , Математические экспозиции Дольчиани № 47, Математическая ассоциация Америки, стр. 251, ISBN 978-0-88385-354-2
- ^ Немецкое название этого круга — Leitkreis , что можно перевести как «круг директоров», но в английской литературе этот термин имеет другое значение (см. Круг директоров ).
- ^ Франс ван Скутен : Mathematische Oeffeningen , Лейден, 1659, стр. 327
- ^ Э. Хартманн: Заметка к лекции «Плоская круговая геометрия», введение в плоскости Мёбиуса, Лагерра и Минковского, стр. 93
- ^ В. Бенц: Vorlesungen über Geomerie der Algebren , Springer (1973)
- ^ Конспект лекций Плоская круговая геометрия, введение в плоскости Мёбиуса, Лагерра и Минковского, С. 33, (PDF; 757 кБ)
- ^ Конспект лекций Плоская круговая геометрия, введение в плоскости Мёбиуса, Лагерра и Минковского, С. 32, (PDF; 757 кБ)
- ^ Fanchi, John R. (2006). Освежение знаний по математике для ученых и инженеров. John Wiley and Sons. Раздел 3.2, страницы 44–45. ISBN 0-471-75715-2.
- ^ Корн, Гранино А.; Корн, Тереза М. (2000). Математический справочник для ученых и инженеров: определения, теоремы и формулы для справки и обзора (второе изд.). Dover Publ. стр. 40.
- ^ Проттер и Морри 1970, стр. APP-29 – APP-30.
- ^ Митчелл, Дуглас У., «Свойство гипербол и их асимптот», Mathematical Gazette 96, июль 2012 г., 299–301.
- ^ JW Downs, Practical Conic Sections , Dover Publ., 2003 (оригинал 1993): стр. 26.
- ^ Кейси, Джон, (1885) «Трактат по аналитической геометрии точки, прямой, окружности и конических сечений, содержащий отчет о ее новейших расширениях с многочисленными примерами»
- ^ Коффман, РТ; Огилви, К.С. (1963), «Свойство отражения» конических сечений», Mathematics Magazine , 36 (1): 11–12, doi :10.2307/2688124 Фландерс, Харли (1968), «Оптические свойства конических сечений», American Mathematical Monthly , 75 (4): 399, doi :10.2307/2313439
Брозинский, Майкл К. (1984), «Свойство отражения эллипса и гиперболы», College Mathematics Journal , 15 (2): 140–42, doi :10.2307/2686519
- ^ "Гипербола". Mathafou.free.fr . Архивировано из оригинала 4 марта 2016 года . Получено 26 августа 2018 года .
- ^ ab "Свойства гиперболы". Архивировано из оригинала 2017-02-02 . Получено 2011-06-22 .
- ^ Карлсон, BC (2010), «Эллиптические интегралы», в Olver, Frank WJ ; Lozier, Daniel M.; Boisvert, Ronald F.; Clark, Charles W. (ред.), NIST Handbook of Mathematical Functions , Cambridge University Press, ISBN 978-0-521-19225-5, г-н 2723248.
- ^ Хейлброн, Джон Л. (1968). «Рассеяние α- и β-частиц и атом Резерфорда». Архив истории точных наук . 4 (4): 247–307. doi :10.1007/BF00411591. ISSN 0003-9519. JSTOR 41133273.
- ^ Так как расстояние от P до точки равно PP' , что равно BP по свойству директрисы и фокуса.
- ^ Эта конструкция принадлежит Паппусу Александрийскому (около 300 г. н.э.), а доказательство взято из Kazarinoff 1970, стр. 62.
Ссылки
- Казаринофф, Николас Д. (1970), Линейка и круг, Бостон: Prindle, Weber & Schmidt, ISBN 0-87150-113-9
- Оукли, штат Колорадо, доктор философии (1944), Очерк исчисления , Нью-Йорк: Barnes & Noble
{{citation}}: CS1 maint: multiple names: authors list (link) - Проттер, Мюррей Х.; Моррей , Чарльз Б. младший (1970), College Calculus with Analytic Geometry (2-е изд.), Reading: Addison-Wesley , LCCN 76087042
Внешние ссылки
- «Гипербола», Энциклопедия математики , EMS Press , 2001 [1994]
- Вывод Аполлония гиперболы при схождении
- Франс ван Скутен: Mathematische Oeffeningen, 1659 г.
- Вайсштейн, Эрик В. «Гипербола». MathWorld .



























































































































































![{\displaystyle t_{0}=\pm {\sqrt[{4}]{\frac {{\vec {f}}_{2}^{2}}{{\vec {f}}_{1} ^{2}}}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6b26de698fecd55664d5a6833e97148678656143)







































![{\displaystyle {\begin{aligned}A_{xx}&=-a^{2}\sin ^{2}\theta +b^{2}\cos ^{2}\theta ,&B_{x}&=-A_{xx}x_{\circ }-A_{xy}y_{\circ },\\[1ex]A_{yy}&=-a^{2}\cos ^{2}\theta +b^{2}\sin ^{2}\theta ,&B_{y}&=-A_{xy}x_{\circ }-A_{yy}y_{\circ },\\[1ex]A_{xy}&=\left(a^{2}+b^{2}\right)\sin \theta \cos \theta ,&C&=A_{xx}x_{\circ }^{2}+2A_{xy}x_{\circ }y_{\circ }+A_{yy}y_{\circ }^{2}-a^{2}b^{2}.\end{align}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f5d82bf36f4898cad69a72588b95496e07d87d0b)



![{\displaystyle {\begin{aligned}x_{c}&=-{\frac {1}{D}}\,{\begin{vmatrix}B_{x}&A_{xy}\\B_{y}&A_{yy}\end{vmatrix}}\,,\\[1ex]y_{c}&=-{\frac {1}{D}}\,{\begin{vmatrix}A_{xx}&B_{x}\\A_{xy}&B_{y}\end{vmatrix}}\,.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ad1cc8fb27ca4ad3d69e8490a1892b0ab44e7807)








![{\displaystyle {\begin{align}a^{2}&=-{\frac {\Delta}{\lambda _{1}D}}=-{\frac {\Delta}{\lambda _{1}^{2}\lambda _{2}}},\\[1ex]b^{2}&=-{\frac {\Delta}{\lambda _{2}D}}=-{\frac {\Delta}{\lambda _{1}\lambda _{2}^{2}}},\end{align}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0d190f3114f60766f993e1a4c00daaf99510f81e)









![{\displaystyle {\begin{aligned}E&=A_{xx}x_{0}+A_{xy}y_{0}+B_{x},\\[1ex]F&=A_{xy}x_{0}+A_{yy}y_{0}+B_{y},\\[1ex]G&=B_{x}x_{0}+B_{y}y_{0}+C.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/467ab27ea151bfad56ade7e716548b668119769c)





































































![{\displaystyle {\begin{cases}x=\pm a{\dfrac {t^{2}+1}{2t}},\\[1ex]y=b{\dfrac {t^{2}-1}{2t}},\end{cases}}\qquad t>0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4638f9752638e31c275c9603c3a41d4dc43c45b6)














![{\displaystyle {\begin{align}{\frac {a}{2}}&={\frac {xy}{2}}-\int _{1}^{x}{\sqrt {t^{2}-1}}\,dt\\[1ex]&={\frac {1}{2}}\left(x{\sqrt {x^{2}-1}}\right)-{\frac {1}{2}}\left(x{\sqrt {x^{2}-1}}-\ln \left(x+{\sqrt {x^{2}-1}}\right)\right),\end{align}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/613cf8b1eff7b14395982b578e9a46790fd7b3fd)
















































![{\displaystyle s=ib{\Biggr [}E\left(iv\,{\Biggr |}\,1+{\frac {a^{2}}{b^{2}}}\right){\Biggr ]}_{\operatorname {arcosh} {\frac {x_{2}}{a}}}^{\operatorname {arcosh} {\frac {x_{1}}{a}}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3f5d0c6796e5b98e06e3a1823868ff218bade95d)
![{\displaystyle s=b\left[F\left(\operatorname {gd} v\,{\Biggr |}-{\frac {a^{2}}{b^{2}}}\right)-E\left(\operatorname {gd} v\,{\Biggr |}-{\frac {a^{2}}{b^{2}}}\right)+{\sqrt {1+{\frac {a^{2}}{b^{2}}}\tanh ^{2}v}}\,\sinh v\right]_{\operatorname {arcosh} {\tfrac {x_{1}}{a}}}^{\operatorname {arcosh} {\tfrac {x_{2}}{a}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/11d1ab93c8a700748cb97ea55602b710787b1250)