ряд Фурье
| Преобразования Фурье |
|---|
Ряд Фурье ( / ˈ f ʊr i eɪ , - i ər / [1] ) представляет собой разложение периодической функции в сумму тригонометрических функций . Ряд Фурье является примером тригонометрического ряда . [2] Выражая функцию в виде суммы синусов и косинусов, многие проблемы, связанные с функцией, становятся проще для анализа, поскольку тригонометрические функции хорошо поняты. Например, ряды Фурье были впервые использованы Жозефом Фурье для нахождения решений уравнения теплопроводности . Это применение возможно, поскольку производные тригонометрических функций укладываются в простые закономерности. Ряды Фурье нельзя использовать для аппроксимации произвольных функций, поскольку большинство функций имеют бесконечно много членов в своих рядах Фурье, и ряды не всегда сходятся . Хорошо ведущие себя функции, например гладкие функции, имеют ряды Фурье, которые сходятся к исходной функции. Коэффициенты ряда Фурье определяются интегралами функции, умноженными на тригонометрические функции, описанными в разделе Ряды Фурье§Определение.
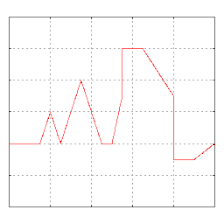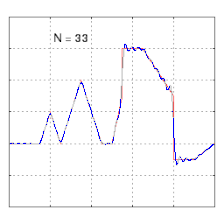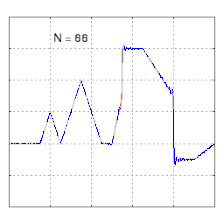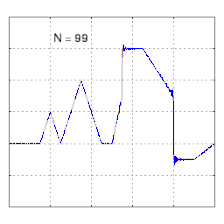
Изучение сходимости рядов Фурье фокусируется на поведении частичных сумм , что означает изучение поведения суммы по мере суммирования все большего числа членов ряда. Рисунки ниже иллюстрируют некоторые результаты частичных рядов Фурье для компонентов прямоугольной волны .
- Прямоугольная волна (представленная синей точкой) аппроксимируется ее шестой частичной суммой (представленной фиолетовой точкой), образованной путем суммирования первых шести членов (представленных стрелками) ряда Фурье прямоугольной волны. Каждая стрелка начинается с вертикальной суммы всех стрелок слева от нее (т. е. предыдущей частичной суммы).
- Первые четыре частичные суммы ряда Фурье для прямоугольной волны . По мере добавления большего количества гармоник частичные суммы сходятся (становятся все более и более похожими) на прямоугольную волну.
- Функция (красного цвета) представляет собой сумму ряда Фурье 6 гармонически связанных синусоид (синего цвета). Ее преобразование Фурье представляет собой представление в частотной области, которое показывает амплитуды суммированных синусоид.
Ряды Фурье тесно связаны с преобразованием Фурье , более общим инструментом, который может даже найти информацию о частоте для функций, которые не являются периодическими. Периодические функции можно отождествить с функциями на окружности; по этой причине ряды Фурье являются предметом анализа Фурье на группе окружности , обозначаемой или . Преобразование Фурье также является частью анализа Фурье , но определено для функций на .
Со времен Фурье было обнаружено много различных подходов к определению и пониманию концепции ряда Фурье, все из которых согласуются друг с другом, но каждый из которых подчеркивает различные аспекты темы. Некоторые из наиболее мощных и элегантных подходов основаны на математических идеях и инструментах, которые не были доступны во времена Фурье. Первоначально Фурье определил ряд Фурье для действительных функций действительных аргументов и использовал функции синуса и косинуса в разложении. С тех пор были определены многие другие преобразования, связанные с Фурье , что расширило его первоначальную идею на многие приложения и породило область математики, называемую анализом Фурье .
История
Ряд Фурье назван в честь Жана-Батиста Жозефа Фурье (1768–1830), который внес важный вклад в изучение тригонометрических рядов после предварительных исследований Леонарда Эйлера , Жана Лерона Д'Аламбера и Даниила Бернулли . [A] Фурье ввел ряд для решения уравнения теплопроводности в металлической пластине, опубликовав свои первоначальные результаты в своем труде 1807 года Mémoire sur la propagation de la chaleur dans les corps solides ( Трактат о распространении тепла в твердых телах ) и опубликовав свой труд Théorie analytique de la chaleur ( Аналитическая теория тепла ) в 1822 году. Mémoire ввел анализ Фурье, в частности ряды Фурье. Благодаря исследованиям Фурье был установлен факт, что произвольная (вначале непрерывная [3] , а затем обобщенная на любую кусочно -гладкую [4] ) функция может быть представлена тригонометрическим рядом. Первое объявление об этом великом открытии было сделано Фурье в 1807 году перед Французской академией . [5] Ранние идеи разложения периодической функции на сумму простых осциллирующих функций восходят к 3 веку до н. э., когда древние астрономы предложили эмпирическую модель движения планет, основанную на деферентах и эпициклах .
Уравнение теплопроводности является частным дифференциальным уравнением . До работы Фурье решение уравнения теплопроводности в общем случае было известно, хотя были известны частные решения, если источник тепла вел себя простым образом, в частности, если источником тепла была синусоидальная или косинусоидальная волна . Эти простые решения теперь иногда называют собственными решениями . Идея Фурье состояла в том, чтобы смоделировать сложный источник тепла как суперпозицию (или линейную комбинацию ) простых синусоидальных и косинусоидальных волн и записать решение как суперпозицию соответствующих собственных решений . Эта суперпозиция или линейная комбинация называется рядом Фурье.
С современной точки зрения результаты Фурье несколько неформальны, ввиду отсутствия точного понятия функции и интеграла в начале девятнадцатого века. Позднее Петер Густав Лежен Дирихле [6] и Бернхард Риман [7] [8] [9] выразили результаты Фурье с большей точностью и формальностью.
Хотя изначальной мотивацией было решение уравнения теплопроводности, позже стало очевидно, что те же методы можно применять к широкому кругу математических и физических задач, и особенно к тем, которые включают линейные дифференциальные уравнения с постоянными коэффициентами, для которых собственные решения являются синусоидами . Ряд Фурье имеет много таких приложений в электротехнике , анализе вибрации , акустике , оптике , обработке сигналов , обработке изображений , квантовой механике , эконометрике , [10] теории оболочек , [11] и т. д.
Начало
Жозеф Фурье писал [12]
Умножая обе части на , а затем интегрируя от до , получаем:
- Жозеф Фурье, «Мемуар о пропаганде шале в твердых телах» (1807).
Это немедленно дает любой коэффициент a k тригонометрического ряда для φ( y ) для любой функции, которая имеет такое расширение. Это работает, потому что если φ имеет такое расширение, то (при подходящих предположениях о сходимости) интеграл можно вычислять почленно. Но все члены, включающие для j ≠ k , исчезают при интегрировании от −1 до 1, оставляя только член, который равен 1 .
В этих нескольких строках, которые близки к современному формализму, используемому в рядах Фурье, Фурье произвел революцию как в математике, так и в физике. Хотя подобные тригонометрические ряды ранее использовались Эйлером , Д'Аламбером , Даниилом Бернулли и Гауссом , Фурье считал, что такие тригонометрические ряды могут представлять любую произвольную функцию. В каком смысле это на самом деле верно — довольно тонкий вопрос, и попытки на протяжении многих лет прояснить эту идею привели к важным открытиям в теориях сходимости , функциональных пространств и гармонического анализа .
Когда Фурье представил позднее конкурсное эссе в 1811 году, комитет (в который входили Лагранж , Лаплас , Малюс и Лежандр , среди прочих) пришел к выводу: ...способ, которым автор приходит к этим уравнениям, не свободен от трудностей, и ...его анализ для их интегрирования все еще оставляет желать лучшего с точки зрения общности и даже строгости . [13]
Мотивация Фурье

Разложение в ряд Фурье пилообразной функции (ниже) выглядит сложнее, чем простая формула , поэтому не сразу становится ясно, зачем нужен ряд Фурье. Хотя существует множество приложений, мотивацией Фурье было решение уравнения теплопроводности . Например, рассмотрим металлическую пластину в форме квадрата, стороны которого измеряются метрами, с координатами . Если внутри пластины нет источника тепла, и если три из четырех сторон поддерживаются при 0 градусах Цельсия, в то время как четвертая сторона, заданная , поддерживается при градиенте температуры градусов Цельсия, для в , то можно показать, что стационарное распределение тепла (или распределение тепла по истечении длительного времени) определяется выражением
Здесь sinh — гиперболическая синусоидальная функция. Это решение уравнения теплопроводности получается путем умножения каждого члена уравнения из Анализ § Пример на . Хотя наша функция-пример, по-видимому, имеет излишне сложный ряд Фурье, распределение тепла нетривиально. Функцию нельзя записать в виде замкнутого выражения . Этот метод решения тепловой задачи стал возможным благодаря работе Фурье.
Другие приложения
Другое применение — решение Базельской проблемы с использованием теоремы Парсеваля . Пример обобщается, и можно вычислить ζ (2 n ), для любого положительного целого числа n .
Определение
Ряд Фурье комплекснозначной P -периодической функции , интегрируемой по интервалу на действительной прямой, определяется как тригонометрический ряд вида , такой, что коэффициенты Фурье являются комплексными числами, определяемыми интегралом [14] [15] Ряд не обязательно сходится (в поточечном смысле), и даже если сходится, он не обязательно равен . Только при выполнении определенных условий (например, если непрерывно дифференцируемо) ряд Фурье сходится к , т. е. Для функций, удовлетворяющих условиям достаточности Дирихле , имеет место поточечная сходимость. [16] Однако это не необходимые условия , и существует много теорем о различных типах сходимости рядов Фурье (например, равномерная сходимость или средняя сходимость ). [17] Определение естественным образом распространяется на ряд Фурье (периодического) распределения ( также называемый рядом Фурье-Шварца ). [18] Тогда ряд Фурье сходится к в распределительном смысле. [19]
Процесс определения коэффициентов Фурье заданной функции или сигнала называется анализом , а построение соответствующего тригонометрического ряда (или его различных приближений) называется синтезом .
Синтез
Ряд Фурье можно записать в нескольких эквивалентных формах, показанных здесь как частичные суммы ряда Фурье : [20]

| Ур.1 |
| Ур.2 |
Гармоники индексируются целым числом, которое также является числом циклов, которые соответствующие синусоиды делают в интервале . Таким образом, синусоиды имеют :
- длина волны равна в тех же единицах, что и .
- частота равна в обратных единицах .
Эти ряды могут представлять функции, которые являются просто суммой одной или нескольких частот в гармоническом спектре . В пределе тригонометрический ряд может также представлять промежуточные частоты и/или несинусоидальные функции из-за бесконечного числа членов.
Анализ
Коэффициенты могут быть заданы/предполагаемы, например, музыкальный синтезатор или временные выборки формы волны. В последнем случае экспоненциальная форма ряда Фурье синтезирует дискретное по времени преобразование Фурье , где переменная представляет частоту вместо времени. В общем случае коэффициенты определяются путем анализа заданной функции, область определения которой представляет собой интервал длины . [B] [21]
| Ур.3 |
Масштабный коэффициент следует из подстановки уравнения 1 в уравнение 3 и использования ортогональности тригонометрической системы . [22] Эквивалентность уравнения 1 и уравнения 2 следует из формулы Эйлера, что приводит к:
где является средним значением на интервале . [23] Обратно:
Пример


Рассмотрим пилообразную функцию: В этом случае коэффициенты Фурье определяются как Можно показать, что ряд Фурье сходится к в каждой точке , где дифференцируемо, и, следовательно: Когда , ряд Фурье сходится к 0, который является полусуммой левого и правого предела при . Это частный случай теоремы Дирихле для рядов Фурье.
Этот пример приводит к решению Базельской проблемы .
Амплитудно-фазовая форма
Если функция имеет вещественные значения, то ряд Фурье можно также представить в виде [24]
| Ур.4 |
где — амплитуда , а — фазовый сдвиг гармоники .
Эквивалентность ур.4 и ур.1 следует из тригонометрического тождества : которое подразумевает [25]

— прямоугольные координаты вектора с полярными координатами , заданные выражением , где — аргумент .
Пример определения параметра для одного значения показан на рисунке 2. Это значение при максимальной корреляции между и шаблоном косинуса . Синий график — это функция взаимной корреляции , также известная как согласованный фильтр :
К счастью, нет необходимости оценивать всю эту функцию, поскольку ее производная равна нулю в максимуме: Следовательно
Общие обозначения
Эта нотация неадекватна для обсуждения коэффициентов Фурье нескольких различных функций. Поэтому ее обычно заменяют модифицированной формой функции ( в данном случае), например, или , а функциональная нотация часто заменяет подстрочную :
В инженерии, особенно когда переменная представляет время, последовательность коэффициентов называется представлением частотной области . Квадратные скобки часто используются, чтобы подчеркнуть, что область этой функции представляет собой дискретный набор частот.
Другое часто используемое представление в частотной области использует коэффициенты ряда Фурье для модуляции гребенки Дирака :
где представляет собой непрерывную частотную область. Когда переменная имеет единицы измерения секунд, имеет единицы измерения герц . «Зубья» гребня расположены на расстоянии, кратном (т.е. гармоникам ) от , что называется основной частотой . может быть восстановлена из этого представления с помощью обратного преобразования Фурье :
Поэтому построенную функцию обычно называют преобразованием Фурье , даже несмотря на то, что интеграл Фурье периодической функции не сходится на гармонических частотах. [C]
Таблица общих рядов Фурье
Некоторые распространённые пары периодических функций и их коэффициенты ряда Фурье показаны в таблице ниже.
- обозначает периодическую функцию с периодом
- обозначим коэффициенты ряда Фурье (синусно-косинусная форма) периодической функции
Таблица основных правил преобразования
В этой таблице показаны некоторые математические операции во временной области и соответствующий эффект в коэффициентах ряда Фурье. Обозначение:
- Комплексное сопряжение обозначается звездочкой.
- обозначают -периодические функции или функции, определенные только для
- обозначим коэффициенты ряда Фурье (показательная форма) и
| Свойство | Временная область | Частотная область (экспоненциальная форма) | Замечания | Ссылка |
|---|---|---|---|---|
| Линейность | ||||
| Обращение времени / Обращение частоты | [27] : стр. 610 | |||
| Спряжение времени | [27] : стр. 610 | |||
| Обращение времени и спряжение | ||||
| Реальная часть во времени | ||||
| Мнимая часть во времени | ||||
| Действительная часть частоты | ||||
| Мнимая часть частоты | ||||
| Сдвиг во времени / Модуляция по частоте | [27] : стр.610 | |||
| Сдвиг по частоте / Модуляция по времени | [27] : стр. 610 |
Характеристики
Симметричные отношения
Когда действительная и мнимая части комплексной функции разлагаются на четную и нечетную части , есть четыре компонента, обозначенные ниже индексами RE, RO, IE и IO. И есть взаимно-однозначное отображение между четырьмя компонентами комплексной временной функции и четырьмя компонентами ее комплексного частотного преобразования: [28] [29]
Из этого очевидны различные соотношения, например :
- Преобразование действительной функции — это сопряженная симметричная функция. Наоборот, сопряженное симметричное преобразование подразумевает действительную временную область.
- Преобразование мнимозначной функции является сопряженной антисимметричной функцией , и обратное утверждение верно.
- Преобразование сопряженной симметричной функции является действительной функцией , и обратное утверждение верно.
- Преобразование сопряженной антисимметричной функции является мнимозначной функцией , и обратное утверждение верно.
Лемма Римана–Лебега
Если интегрируемо , и
Теорема Парсеваля
Если принадлежит (периодическому на интервале длины ), то:
Теорема Планшереля
Если — коэффициенты и тогда существует единственная функция такая, что для каждого .
Теоремы о свертке
Даны -периодические функции, и с коэффициентами ряда Фурье и
- Точечное произведение : также является -периодическим, а его коэффициенты ряда Фурье задаются дискретной сверткой последовательностей и :
- Периодическая свертка : также является -периодической, с коэффициентами ряда Фурье :
- Дважды бесконечная последовательность в является последовательностью коэффициентов Фурье функции в тогда и только тогда , когда она является сверткой двух последовательностей в . См. [30]
Производное свойство
Если — 2 π -периодическая функция, на которой дифференцируема по разу, а ее производная непрерывна, то принадлежит функциональному пространству .
- Если , то коэффициенты Фурье производной можно выразить через коэффициенты Фурье , с помощью формулы В частности, поскольку для любого фиксированного имеем при , то следует, что стремится к нулю, т.е. коэффициенты Фурье стремятся к нулю быстрее, чем степень .
Компактные группы
Одно из интересных свойств преобразования Фурье, о котором мы упомянули, заключается в том, что оно переносит свертки в поточечные произведения. Если это свойство мы стремимся сохранить, то можно производить ряды Фурье на любой компактной группе . Типичные примеры включают те классические группы , которые являются компактными. Это обобщает преобразование Фурье на все пространства вида L 2 ( G ), где G — компактная группа, таким образом, что преобразование Фурье переносит свертки в поточечные произведения. Ряд Фурье существует и сходится аналогично случаю [− π , π ] .
Альтернативным расширением для компактных групп является теорема Петера–Вейля , которая доказывает результаты о представлениях компактных групп, аналогичные результатам о конечных группах.

Римановы многообразия
Если область не является группой, то нет внутренне определенной свертки. Однако, если — компактное риманово многообразие , оно имеет оператор Лапласа–Бельтрами . Оператор Лапласа–Бельтрами — это дифференциальный оператор, который соответствует оператору Лапласа для риманова многообразия . Тогда, по аналогии, можно рассмотреть уравнения теплопроводности на . Поскольку Фурье пришел к своему базису, пытаясь решить уравнение теплопроводности, естественным обобщением является использование собственных решений оператора Лапласа–Бельтрами в качестве базиса. Это обобщает ряд Фурье на пространства типа , где — риманово многообразие. Ряд Фурье сходится способами, аналогичными случаю . Типичным примером является взятие сферы с обычной метрикой, в этом случае базис Фурье состоит из сферических гармоник .
Локально компактные абелевы группы
Обобщение на компактные группы, обсуждавшееся выше, не распространяется на некомпактные, неабелевы группы . Однако существует прямое обобщение на локально компактные абелевы группы (LCA) .
Это обобщает преобразование Фурье до или , где — группа LCA. Если компактно, то также получается ряд Фурье, который сходится аналогично случаю , но если некомпактно, то вместо этого получается интеграл Фурье . Это обобщение дает обычное преобразование Фурье , когда базовая локально компактная абелева группа — .
Расширения
Ряд Фурье-Стилтьеса
Пусть — функция ограниченной вариации, определенная на замкнутом инвервале . Ряд Фурье, коэффициенты которого задаются формулой [31], называется рядом Фурье-Стилтьеса . Пространство функций ограниченной вариации является подпространством . Поскольку любое определяет меру Радона (т.е. локально конечную меру Бореля на ), это определение можно расширить следующим образом.
Рассмотрим пространство всех конечных мер Бореля на вещественной прямой; как таковое . [32] Если существует мера такая, что коэффициенты Фурье-Стилтьеса задаются как , то ряд называется рядом Фурье-Стилтьеса. Аналогично, функция , где , называется преобразованием Фурье-Стилтьеса . [33]
Вопрос о том, существует ли для данной последовательности , лежит в основе тригонометрической проблемы моментов . [34]
Кроме того, является строгим подпространством пространства (умеренных) распределений , т.е. . Если коэффициенты Фурье определяются распределением , то ряд описывается как ряд Фурье-Шварца . В отличие от ряда Фурье-Стилтьеса, решение о том, является ли данный ряд рядом Фурье или рядом Фурье-Шварца, относительно тривиально из-за характеристик его двойственного пространства; пространства Шварца . [35]
Ряд Фурье по квадрату
Мы также можем определить ряд Фурье для функций двух переменных и в квадрате :
Помимо того, что ряды Фурье на квадрате полезны для решения уравнений с частными производными, таких как уравнение теплопроводности, одно из заметных применений рядов Фурье на квадрате — сжатие изображений . В частности, стандарт сжатия изображений JPEG использует двумерное дискретное косинусное преобразование , дискретную форму косинусного преобразования Фурье , которая использует только косинус в качестве базисной функции.
Для двумерных массивов с шахматным расположением половина коэффициентов ряда Фурье исчезает из-за дополнительной симметрии. [36]
Ряд Фурье решётки Браве-периодической-функции
Трехмерная решетка Бравэ определяется как набор векторов вида: где — целые числа, а — три линейно независимых вектора. Предполагая, что у нас есть некоторая функция, , такая, что она подчиняется условию периодичности для любого вектора решетки Бравэ , , мы могли бы составить ряд Фурье для нее. Такого рода функцией может быть, например, эффективный потенциал, который один электрон «чувствует» внутри периодического кристалла. Полезно составить ряд Фурье для потенциала при применении теоремы Блоха . Во-первых, мы можем записать любой произвольный вектор положения в системе координат решетки: где значение , которое определяется как величина , поэтому единичный вектор направлен вдоль .
Таким образом, мы можем определить новую функцию,
Эта новая функция, , теперь является функцией трех переменных, каждая из которых имеет периодичность , , и соответственно:
Это позволяет нам построить набор коэффициентов Фурье, каждый из которых индексируется тремя независимыми целыми числами . В дальнейшем мы используем нотацию функций для обозначения этих коэффициентов, тогда как ранее мы использовали индексы. Если мы запишем ряд для на интервале для , мы можем определить следующее:
И тогда мы можем написать:
Дальнейшее определение:
Мы можем записать еще раз так:
Наконец, применяя то же самое к третьей координате, определяем:
Мы пишем так:
Перестановка:
Теперь каждый вектор обратной решетки может быть записан (но это не означает, что это единственный способ записи) как , где — целые числа, а — векторы обратной решетки, удовлетворяющие ( для и для ). Тогда для любого произвольного вектора обратной решетки и произвольного вектора положения в исходном пространстве решетки Браве их скалярное произведение равно:
Итак, очевидно, что в нашем разложении сумма фактически идет по векторам обратной решетки:
где
Предполагая, что мы можем решить эту систему из трех линейных уравнений относительно , , и в терминах , и для того, чтобы вычислить элемент объема в исходной прямоугольной системе координат. Как только у нас есть , , и в терминах , и , мы можем вычислить определитель Якоби : который после некоторых вычислений и применения некоторых нетривиальных тождеств перекрестного произведения может быть показан равным:
(может быть выгодно для упрощения вычислений работать в такой прямоугольной системе координат, в которой так уж получается, что параллельна оси x , лежит в плоскости xy и имеет компоненты всех трех осей). Знаменатель — это в точности объем примитивной элементарной ячейки, которая заключена между тремя примитивными векторами , и . В частности, теперь мы знаем, что
Теперь мы можем записать как интеграл с традиционной системой координат по объему примитивной ячейки, вместо переменных , и : записывая для элемента объема ; и где — примитивная элементарная ячейка, таким образом, — объем примитивной элементарной ячейки.
Гильбертово пространство
Поскольку тригонометрический ряд является специальным классом ортогональной системы , ряд Фурье может быть естественным образом определен в контексте гильбертовых пространств . Например, пространство квадратично интегрируемых функций на образует гильбертово пространство . Его скалярное произведение , определенное для любых двух элементов и , задается как: Это пространство снабжено ортонормированным базисом . Тогда (обобщенное) разложение в ряд Фурье для , заданное как , можно записать как [37]

Форма синуса-косинуса получается аналогичным образом. Действительно, синусы и косинусы образуют ортогональный набор : (где δ mn — символ Кронекера ), и Следовательно, набор также образует ортонормированный базис для . Плотность их охвата является следствием теоремы Стоуна–Вейерштрасса , но также следует из свойств классических ядер, таких как ядро Фейера .
Теорема Фурье, доказывающая сходимость ряда Фурье
В инженерии ряд Фурье обычно предполагается сходящимся, за исключением скачков непрерывности, поскольку функции, встречающиеся в инженерии, обычно ведут себя лучше, чем функции в других дисциплинах. В частности, если является непрерывным и производная (которая может существовать не везде) интегрируема с квадратом, то ряд Фурье сходится абсолютно и равномерно к . [38] Если функция интегрируема с квадратом на интервале , то ряд Фурье сходится к функции почти всюду . Можно определить коэффициенты Фурье для более общих функций или распределений, в этом случае поточечная сходимость часто не удается, и обычно изучается сходимость в норме или слабая сходимость .
- Четыре частичные суммы (ряды Фурье) длиной 1, 2, 3 и 4 члена, показывающие, как улучшается приближение к прямоугольной волне по мере увеличения числа членов (анимация)
- Четыре частичные суммы (ряды Фурье) длиной 1, 2, 3 и 4 члена, показывающие, как приближение к пилообразной волне улучшается по мере увеличения числа членов (анимация)
- Пример сходимости к несколько произвольной функции. Обратите внимание на развитие "звона" ( явление Гиббса ) при переходах к/от вертикальных участков.
Теоремы, доказывающие, что ряд Фурье является допустимым представлением любой периодической функции (удовлетворяющей условиям Дирихле ), и их неформальные вариации, не определяющие условия сходимости, иногда в общем виде называются теоремой Фурье или теоремой Фурье . [39] [40] [41] [42]
Свойство наименьших квадратов
Предыдущее уравнение 2 :
— тригонометрический полином степени , который в общем случае можно выразить как :
Теорема Парсеваля подразумевает, что:
Теорема — Тригонометрический полином является единственным наилучшим тригонометрическим полиномом степени , приближающим , в том смысле, что для любого тригонометрического полинома степени , мы имеем: где норма гильбертова пространства определяется как:
Теоремы сходимости
Благодаря свойству наименьших квадратов и полноте базиса Фурье мы получаем элементарный результат сходимости.
Теорема — Если принадлежит , то сходится к в при , то есть:
Если непрерывно дифференцируема, то — коэффициент Фурье первой производной . Поскольку непрерывна и, следовательно, ограничена, она квадратично интегрируема , а ее коэффициенты Фурье квадратично суммируемы. Тогда, по неравенству Коши–Шварца ,
Это означает, что является абсолютно суммируемым . Сумма этого ряда является непрерывной функцией, равной , поскольку ряд Фурье сходится к :
Теорема — Если , то сходится к равномерно .
Этот результат можно легко доказать, если дополнительно предположить, что , поскольку в этом случае стремится к нулю при . В более общем случае ряд Фурье абсолютно суммируем, поэтому сходится равномерно к , при условии, что удовлетворяет условию Гёльдера порядка . В абсолютно суммируемом случае неравенство:
доказывает равномерную сходимость.
Известно много других результатов, касающихся сходимости рядов Фурье, начиная от сравнительно простого результата о том, что ряд сходится при , если дифференцируем в , до более сложных результатов, таких как теорема Карлесона , утверждающая, что ряд Фурье функции сходится почти всюду .
Дивергенция
Поскольку ряды Фурье обладают такими хорошими свойствами сходимости, многие часто удивляются некоторым отрицательным результатам. Например, ряд Фурье непрерывной T -периодической функции не обязательно сходится поточечно. Принцип равномерной ограниченности дает простое неконструктивное доказательство этого факта.
В 1922 году Андрей Колмогоров опубликовал статью под названием « Une série de Fourier-Lebesgue divergente presque partout» , в которой он привел пример интегрируемой по Лебегу функции, ряд Фурье которой расходится почти всюду. Позднее он построил пример интегрируемой функции, ряд Фурье которой расходится всюду. [43]
Можно привести явные примеры непрерывной функции, ряд Фурье которой расходится в точке 0: например, четная и 2π-периодическая функция f, определенная для всех x в [0,π] формулой [44]
Поскольку функция четная, ряд Фурье содержит только косинусы:
Коэффициенты:
По мере увеличения m коэффициенты будут положительными и увеличиваться, пока не достигнут значения около при для некоторого n , а затем станут отрицательными (начиная со значения около ) и будут уменьшаться, прежде чем начнется новая такая волна. При ряд Фурье — это просто текущая сумма , и это накапливается до около
в n -й волне перед возвращением к нулю, показывая, что ряд не сходится в нуле, а достигает все более высоких пиков. Обратите внимание, что хотя функция непрерывна, она не дифференцируема.
Смотрите также
- Теорема ATS
- Теорема Карлесона
- ядро Дирихле
- Дискретное преобразование Фурье
- Быстрое преобразование Фурье
- Теорема Фейера
- анализ Фурье
- Теорема обращения Фурье
- Ряды Фурье по синусам и косинусам
- преобразование Фурье
- явление Гиббса
- Половина диапазона ряда Фурье
- Ряд Лорана – подстановка q = e ix преобразует ряд Фурье в ряд Лорана, или наоборот. Это используется в разложении j -инварианта в q -ряд .
- Спектральный анализ методом наименьших квадратов
- Многомерное преобразование
- Теорема вычета интегралов f ( z ), сингулярности, полюса
- Синусные и косинусные преобразования
- Спектральная теория
- Теория Штурма–Лиувилля
- Тригонометрическая проблема моментов
Примечания
- ^ Эти трое сделали некоторые важные ранние работы по волновому уравнению , особенно Даламбер. Работа Эйлера в этой области была в основном одновременной/в сотрудничестве с Бернулли , хотя последний внес некоторые независимые вклады в теорию волн и колебаний. (См. Fetter & Walecka 2003, стр. 209–210).
- ^ Обычно или . Некоторые авторы определяют , потому что это упрощает аргументы синусоидальных функций за счет общности.
- ^ Поскольку интеграл, определяющий преобразование Фурье периодической функции, не является сходящимся, необходимо рассматривать периодическую функцию и ее преобразование как распределения . В этом смысле является дельта-функцией Дирака , которая является примером распределения.
Ссылки
- ^ "Фурье". Dictionary.com Unabridged (Online). nd
- ^ Зигмунд 2002, стр. 1-8.
- ^ Стиллвелл, Джон (2013). «Логика и философия математики в девятнадцатом веке». В Ten, CL (ред.). Routledge History of Philosophy . Том VII: Девятнадцатый век. Routledge. стр. 204. ISBN 978-1-134-92880-4.
- ^ Фасшауэр, Грег (2015). «Ряды Фурье и краевые задачи» (PDF) . Заметки к курсу Math 461, Глава 3 . Кафедра прикладной математики, Иллинойсский технологический институт . Получено 6 ноября 2020 г. .
- ^ Каджори, Флориан (1893). История математики. Macmillan. стр. 283.
- ^ Лежен-Дирихле, Питер Густав (1829). «Sur la сходимость тригонометрических рядов, которые служат представителем произвольной функции между двумя заданными пределами» [О сходимости тригонометрических рядов, которые служат для представления произвольной функции между двумя заданными пределами]. Journal für die reine und angewandte Mathematik (на французском языке). 4 : 157–169 . arXiv : 0806.1294 .
- ^ "Ueber die Darstellbarkeit einer Function durch eine trigonometrische Reihe" [О представимости функции тригонометрическим рядом]. Habilitationsschrift , Геттинген ; 1854. Abhandlungen der Königlichen Gesellschaft der Wissenschaften zu Göttingen , vol. 13, 1867. Опубликовано посмертно для Римана Рихардом Дедекиндом (на немецком языке). Архивировано из оригинала 20 мая 2008 года . Проверено 19 мая 2008 г.
- ^ Маскр, Д.; Риман, Бернхард (1867), «Посмертная диссертация о представлении функций тригонометрическими рядами», в Grattan-Guinness, Ivor (ред.), Landmark Writings in Western Mathematics 1640–1940, Elsevier (опубликовано в 2005 г.), стр. 49, ISBN 9780080457444
- ^ Реммерт, Рейнхольд (1991). Теория комплексных функций: Чтения по математике. Springer. стр. 29. ISBN 9780387971957.
- ^ Нерлав, Марк; Гретер, Дэвид М.; Карвальо, Хосе Л. (1995). Анализ экономических временных рядов. Экономическая теория, эконометрика и математическая экономика . Elsevier. ISBN 0-12-515751-7.
- ^ Вильгельм Флюгге , Напряжения в оболочках (1973), 2-е издание. ISBN 978-3-642-88291-3 . Первоначально опубликовано на немецком языке как Statik und Dynamik der Schalen (1937).
- ^ Фурье, Жан-Батист-Жозеф (1890). «Мемуар о пропаганде Chaleur dans les Corps Solides, представленный 21 декабря 1807 года в Национальном институте». В Гастоне Дарбу (ред.). Oeuvres de Fourier [ Работы Фурье ] (на французском языке). Том. 2. Париж: Готье-Виллар и Филс. стр. 218–219 . doi : 10.1017/CBO9781139568159.009. ISBN 9781139568159. Хотя в цитируемой статье автором указан Фурье, сноска на странице 215 указывает, что статья на самом деле была написана Пуассоном и что она, «по соображениям исторического интереса», представлена так, как если бы это были оригинальные мемуары Фурье.
- ^ Фурье, Жан-Батист-Жозеф (1888). «Авангард произведений Фурье». В Гастоне Дарбу (ред.). Oeuvres de Fourier [ Работы Фурье ] (на французском языке). Том. 1. Париж: Готье-Виллар и Филс. стр. VII– VIII. дои : 10.1017/cbo9781139568081.001. ISBN 978-1-108-05938-1.
- ↑ Фолланд 1992, стр. 18–25.
- ↑ Харди и Рогозински 1999, стр. 2–4.
- ↑ Лев 1986.
- ↑ Эдвардс 1979, стр. 8–9.
- ↑ Эдвардс 1982, стр. 57, 67.
- ↑ Шварц 1966, стр. 152–158.
- ^ Стрэнг, Гилберт (2008), "4.1" (PDF) , Ряды Фурье и интегралы (2-е изд.), Wellesley-Cambridge Press, стр. 323 (eq 19)
- ^ Штаде 2005, стр. 6.
- ^ Зигмунд, Антони (1935). «Тригонометрические ряды». EUDML . стр. 6. Получено 14.12.2024 .
- ↑ Фолланд 1992, стр. 21.
- ↑ Штаде 2005, стр. 59–64.
- ^ Кассам, Салим А. (2004). "Ряд Фурье (часть II)" (PDF) . Получено 2024-12-11 .
Фазовые соотношения важны, поскольку они соответствуют наличию различных величин "временных сдвигов" или "задержек" для каждой из синусоидальных волн относительно волны с нулевой фазой.
- ^ abcde Папула, Лотар (2009). Mathematische Formelsammlung: für Ingenieure und Naturwissenschaftler [ Математические функции для инженеров и физиков ] (на немецком языке). Vieweg+Teubner Verlag. ISBN 978-3834807571.
- ^ abcd Шмалий, YS (2007). Сигналы непрерывного времени . Springer. ISBN 978-1402062711.
- ^ Проакис и Манолакис 1996, с. 291.
- ^ Оппенгейм и Шефер 2010, стр. 55.
- ^ "Характеристики линейного подпространства, связанного с рядами Фурье". MathOverflow. 2010-11-19 . Получено 2014-08-08 .
- ^ Зигмунд 2002, стр. 11.
- ^ Кацнельсон 2004, стр. 144.
- ↑ Эдвардс 1982, стр. 53, 67, 72.
- ↑ Ахиезер 1965, стр. 180–181.
- ↑ Эдвардс 1982, стр. 57, 67–68.
- ^ Обращение в нуль половины коэффициентов Фурье в шахматных решетках
- ^ Рудин 1987, стр. 82.
- ^ Толстов, Георгий П. (1976). Ряды Фурье. Courier-Dover. ISBN 0-486-63317-9.
- ^ Siebert, William McC. (1985). Схемы, сигналы и системы. MIT Press. стр. 402. ISBN 978-0-262-19229-3.
- ^ Мартон, Л.; Мартон, Клэр (1990). Достижения в области электроники и электронной физики. Academic Press. стр. 369. ISBN 978-0-12-014650-5.
- ^ Кузмани, Ганс (1998). Твердотельная спектроскопия. Springer. стр. 14. ISBN 978-3-540-63913-8.
- ^ Прибрам, Карл Х.; Ясуэ, Кунио; Джибу, Мари (1991). Мозг и восприятие. Лоуренс Эрлбаум Ассошиэйтс. п. 26. ISBN 978-0-89859-995-4.
- ^ Кацнельсон 2004.
- ^ Гурдон, Ксавье (2009). Математика наедине. Анализируйте (2ème edition) (на французском языке). Эллипсы. п. 264. ИСБН 978-2729837594.
Библиография
- Ахиезер, NI (1965). Классическая проблема моментов и некоторые связанные с ней вопросы анализа. Филадельфия, Пенсильвания: Общество промышленной и прикладной математики. doi : 10.1137/1.9781611976397 . ISBN 978-1-61197-638-0.
- Boyce, William E.; DiPrima, Richard C. (2005). Elementary Differential Equations and Boundary Value Problems (8-е изд.). Нью-Джерси: John Wiley & Sons, Inc. ISBN 0-471-43338-1.
- Эдвардс, Р. Э. (1979). Ряды Фурье . Том 64. Нью-Йорк, Нью-Йорк: Springer New York. doi :10.1007/978-1-4612-6208-4. ISBN 978-1-4612-6210-7.
- Эдвардс, Р. Э. (1982). Ряды Фурье . Т. 85. Нью-Йорк, Нью-Йорк: Springer New York. doi :10.1007/978-1-4613-8156-3. ISBN 978-1-4613-8158-7.
- Фурье, Жозеф (2003). Аналитическая теория тепла . Dover Publications. ISBN 0-486-49531-0.Полное переиздание в 2003 году английского перевода работы Фурье «Аналитическая теория тепла» , выполненного Александром Фрименом в 1878 году и первоначально опубликованного в 1822 году.
- Феттер, Александр Л.; Валецка, Джон Дирк (2003). Теоретическая механика частиц и сплошных сред. Courier. ISBN 978-0-486-43261-8.
- Фолланд, Джеральд Б. (1992). Анализ Фурье и его приложения . Пасифик Гроув, Калифорния: Wadsworth & Brooks/Cole. ISBN 978-0-534-17094-3.
- Гонсалес-Веласко, Энрике А. (1992). «Связи в математическом анализе: случай рядов Фурье». American Mathematical Monthly . 99 (5): 427– 441. doi :10.2307/2325087. JSTOR 2325087.
- Харди, ГХ ; Рогозинский, Вернер (1999). Ряды Фурье . Минеола, Нью-Йорк: Dover Publications. ISBN 978-0-486-40681-7.
- Кацнельсон, Ицхак (2004). Введение в гармонический анализ . Cambridge University Press. doi :10.1017/cbo9781139165372. ISBN 978-0-521-83829-0.
- Кхаре, Кедар; Бутола, Манси; Раджора, Сунайна (2023). Фурье-оптика и вычислительная визуализация . Cham: Springer International Publishing. doi : 10.1007/978-3-031-18353-9. ISBN 978-3-031-18352-2.
- Кляйн, Феликс (1979). Развитие математики в 19 веке . Бруклин, Массачусетс: Math Science Press. ISBN 978-0-915692-28-6.Перевод М. Акермана из Vorlesungen über die Entwicklung der Mathematik im 19 Jahrhundert , Springer, Берлин, 1928.
- Лион, Жорж А. (1986). «Простое доказательство теста сходимости Дирихле-Жордана». The American Mathematical Monthly . 93 (4): 281– 282. doi :10.1080/00029890.1986.11971805. ISSN 0002-9890.
- Оппенгейм, Алан В.; Шефер, Рональд В. (2010). Обработка сигналов в дискретном времени . Upper Saddle River Munich: Prentice Hall. стр. 55. ISBN 978-0-13-198842-2.
- Проакис, Джон Г.; Манолакис, Димитрис Г. (1996). Цифровая обработка сигналов: принципы, алгоритмы и приложения (3-е изд.). Prentice Hall. ISBN 978-0-13-373762-2.
- Рудин, Уолтер (1976). Принципы математического анализа (3-е изд.). Нью-Йорк: McGraw-Hill, Inc. ISBN 0-07-054235-X.
- Рудин, Уолтер (1987). Действительный и комплексный анализ . Нью-Йорк, Нью-Йорк: McGraw-Hill Education. ISBN 978-0-07-100276-9.
- Штейд, Эрик (2005). Анализ Фурье . Wiley. doi :10.1002/9781118165508. ISBN 978-0-471-66984-5.
- Шварц, Лоран (1966). Математика для физических наук. Париж и Рединг, Массачусетс: Hermann/Addison-Wesley Publishing.
- Зигмунд, А. (2002). Тригонометрические ряды (третье изд.). Кембридж: Cambridge University Press. ISBN 0-521-89053-5.Первое издание вышло в 1935 году.
Внешние ссылки
- «Ряды Фурье», Энциклопедия математики , EMS Press , 2001 [1994]
- Хобсон, Эрнест (1911). . Encyclopaedia Britannica . Т. 10 (11-е изд.). С. 753–758 .
- Вайсштейн, Эрик В. "Ряды Фурье". MathWorld .
- Жозеф Фурье – Сайт о жизни Фурье, который был использован для исторического раздела этой статьи на Wayback Machine (архивировано 5 декабря 2001 г.)
В данной статье использованы материалы из примера ряда Фурье на PlanetMath , лицензированного по лицензии Creative Commons Attribution/Share-Alike License .


















![{\displaystyle (x,y)\in [0,\pi ]\times [0,\pi ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c18734f151b17b5d3e325f79c7000826ab832610)









![{\displaystyle [0,P]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e22a95e69fea5905acab328644408c110eedea0e)





















![{\displaystyle (-\пи ,\пи ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7fbb1843079a9df3d3bbcce3249bb2599790de9c)


![{\displaystyle {\begin{aligned}s(x)&=a_{_{0}}+\sum _{n=1}^{\infty }\left[a_{_{n}}\cos \left(nx\right)+b_{_{n}}\sin \left(nx\right)\right]\\[4pt]&={\frac {2}{\pi }}\sum _{n=1}^{\infty }{\frac {(-1)^{n+1}}{n}}\sin(nx),\quad \mathrm {для} \ (x-\pi )\ {\text{не кратно}}\ 2\pi .\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/abed66f2a1bb3406686a9467e297ca03b0da003b)













![{\displaystyle {\begin{aligned}\mathrm {X} (\varphi )&=\int _{P}s(x)\cdot \cos \left(2\pi {\tfrac {n}{P}}x-\varphi \right)\,dx\quad \varphi \in \left[0,2\pi \right]\\&=\cos(\varphi )\underbrace {\int _{P}s(x)\cdot \cos \left(2\pi {\tfrac {n}{P}}x\right)dx} _{X(0)}+\sin(\varphi )\underbrace {\int _{P}s(x)\cdot \sin \left(2\pi {\tfrac {n}{P}}x\right)dx} _{X(\pi /2)}\end{выровнено}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c730a42e4648bdd9563ee9b626da675c870a106b)




![{\displaystyle S[n],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/05512880c069e82fff8d239382be51f091900527)
![{\displaystyle {\begin{aligned}s(x)&=\sum _{n=-\infty }^{\infty }{\widehat {s}}(n)\cdot e^{i2\pi {\tfrac {n}{P}}x}&&\scriptstyle {\text{общепринятая математическая нотация}}\\&=\sum _{n=-\infty }^{\infty }S[n]\cdot e^{i2\pi {\tfrac {n}{P}}x}&&\scriptstyle {\text{общепринятая инженерная нотация}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ab1656144664ad56f8ed36ac280fbf9401ea7da9)
![{\displaystyle S(f)\ \triangleq \ \sum _{n=-\infty }^{\infty }S[n]\cdot \delta \left(f-{\frac {n}{P}}\right),}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e6a4127cd2d8d239076aad35e6b82248554b6036)


![{\displaystyle {\begin{aligned}{\mathcal {F}}^{-1}\{S(f)\}&=\int _{-\infty }^{\infty }\left(\sum _{n=-\infty }^{\infty }S[n]\cdot \delta \left(f-{\frac {n}{P}}\right)\right)e^{i2\pi fx}\,df,\\[6pt]&=\sum _{n=-\infty }^{\infty }S[n]\cdot \int _{-\infty }^{\infty }\delta \left(f-{\frac {n}{P}}\right)e^{i2\pi fx}\,df,\\[6pt]&=\sum _{n=-\infty }^{\infty }S[n]\cdot e^{i2\pi {\tfrac {n}{P}}x}\ \ \triangleq \ s(x).\end{align}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8732ce9daf2bec042faf4a0aa53e97979398d29f)








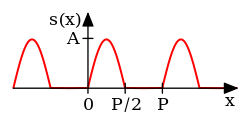






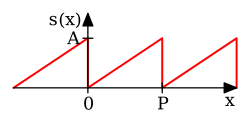








![{\displaystyle x\in [0,P].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/06b058e43f16179590921d9669ac45cec21a975e)
![{\displaystyle S[n],R[n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/320b593144d771f4aac1aae12d9513debbd3b20f)


![{\displaystyle a\cdot S[n]+b\cdot R[n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/23622be4a50d54928d05c273e803240a2cb1e413)


![{\displaystyle S[-n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ab628b28c49c04cab81d0bd30d19ee0797b0587c)

![{\displaystyle S^{*}[-n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a3f6ea8a947b86f8a31046070359f6b8111a0bae)

![{\displaystyle S^{*}[н]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3776c67c40997d8044720ef84de7575679cf9638)

![{\displaystyle {\frac {1}{2}}(S[n]+S^{*}[-n])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2eb44dffaae6c85870914249c054e33236b02cc8)

![{\displaystyle {\frac {1}{2i}}(S[n]-S^{*}[-n])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bc039a9c12ae20a4b47337ae55bf8a7bc26d2e11)

![{\displaystyle \operatorname {Re} {(S[n])}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/140ebff319eb8eb7965d0ca86dcaadb21685177a)

![{\displaystyle \operatorname {Я} {(S[n])}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0c726948120015ce0d482f5f7f4af81713342b5c)

![{\displaystyle S[n]\cdot e^{-i2\pi {\tfrac {x_{0}}{P}}n}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7c56731e1382c8189ca81104cbade4d310fd72d8)


![{\displaystyle S[n-n_{0}]\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/07385c0e5fd45d4e07a279a91668cf8894963e0c)











![{\textstyle \lim _{|n|\to \infty }S[n]=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7fc04d857f6462ae29422edcada981c8a798d4b5)



![{\displaystyle {\frac {1}{P}}\int _{P}|s(x)|^{2}\,dx=\sum _{n=-\infty }^{\infty }{\Bigl |}S[n]{\Bigr |}^{2}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/79bfe83e4422855ccd3c607f3154e3ac5008aaa5)



![{\displaystyle S[n]=c_{n}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c4375307afdf29e78a31ef64b699dcb3e2fde140)


![{\displaystyle S[n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0b4222b53917b43f530116997b71049100c95586)
![{\displaystyle R[n],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/80d8bbe147f3eb3fb318d09437a3540e054b0289)



![{\displaystyle H[n]=\{S*R\}[n].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b5d3978629d1c2cd954f884509a1bb360f01cac5)

![{\displaystyle H[n]=P\cdot S[n]\cdot R[n].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1804f502413d4e3e5f28f8715c52e2a3d7e7e9a6)


![{\displaystyle L^{1}([0,2\pi])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bd16426bda528c05e32e97bfba7f51b598c081b8)





![{\displaystyle {\widehat {s}}[n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/efb5adbeb52d198894dc8f70ec8c434f0e193e6b)
![{\displaystyle {\widehat {s^{(k)}}}[n]=(дюйм)^{k}{\widehat {s}}[n].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3eabad0ea37b7c05c6059b1d40249aa632ea9b18)

![{\displaystyle {\widehat {s^{(k)}}}[n]\to 0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0ddeff4d322091a8ec85a30a10d584d426d703b1)

![{\displaystyle |n|^{k}{\widehat {s}}[n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/541244c281f9472e99fca9b32f2cd7676434d09c)



![{\displaystyle [-\пи ,\пи ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cb064fd6c55820cfa660eabeeda0f6e3c4935ae6)




![{\displaystyle [0,P]\subseteq \mathbb {R} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/4b2f4786ea3e741cdd539bf05c05fa4383a441e4)















![{\displaystyle [-\пи,\пи]\times [-\пи,\пи]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/df436805f50de7386abdb2a9d058672ec1b4cebb)
![{\displaystyle {\begin{aligned}f(x,y)&=\sum _{j,k\in \mathbb {Z} }c_{j,k}e^{ijx}e^{iky},\ \[5pt]c_{j,k}&={\frac {1}{4\pi ^{2}}}\int _{-\pi }^{\pi }\int _{-\pi }^{\pi }f(x,y)e^{-ijx}e^{-iky}\,dx\,dy.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/aec3723d7051701ab4530dce39f1480cef835981)



















![{\displaystyle \left[0,a_{1}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/187cf2c27876a96c668f73266f673002808773ac)



![{\displaystyle {\begin{aligned}h^{\mathrm {два} }(m_{1},m_{2},x_{3})&\треугольникq {\frac {1}{a_{2}}}\int _{0}^{a_{2}}h^{\mathrm {один} }(m_{1},x_{2},x_{3})\cdot e^{-i2\пи {\tfrac {m_{2}}{a_{2}}}x_{2}}\,dx_{2}\\[12pt]&={\frac {1}{a_{2}}}\int _{0}^{a_{2}}dx_{2}{\frac {1}{a_{1}}}\int _{0}^{a_{1}}dx_{1}g(x_{1},x_{2},x_{3})\cdot e^{-i2\pi \left({\tfrac {m_{1}}{a_{1}}}x_{1}+{\tfrac {m_{2}}{a_{2}}}x_{2}\right)}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/257f40440f195f996a7a7df57b110f544e8553c6)

![{\displaystyle {\begin{aligned}h^{\mathrm {три} }(m_{1},m_{2},m_{3})&\треугольникq {\frac {1}{a_{3}}}\int _{0}^{a_{3}}h^{\mathrm {два} }(m_{1},m_{2},x_{3})\cdot e^{-i2\pi {\tfrac {m_{3}}{a_{3}}}x_{3}}\,dx_{3}\\[12pt]&={\frac {1}{a_{3}}}\int _{0}^{a_{3}}dx_{3}{\frac {1}{a_{2}}}\int _{0}^{a_{2}}dx_{2}{\frac {1}{a_{1}}}\int _{0}^{a_{1}}dx_{1}g(x_{1},x_{2},x_{3})\cdot e^{-i2\pi \left({\tfrac {m_{1}}{a_{1}}}x_{1}+{\tfrac {m_{2}}{a_{2}}}x_{2}+{\tfrac {m_{3}}{a_{3}}}x_{3}\right)}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e16c337b17dc4ed299de47b108a2ff7eb060b9f3)



















![{\displaystyle {\begin{vmatrix}{\dfrac {\partial x_{1}}{\partial x}}&{\dfrac {\partial x_{1}}{\partial y}}&{\dfrac {\partial x_{1}}{\partial z}}\\[12pt]{\dfrac {\partial x_{2}}{\partial x}}&{\dfrac {\partial x_{2}}{\partial y}}&{\dfrac {\partial x_{2}}{\partial z}}\\[12pt]{\dfrac {\partial x_{3}}{\partial x}}&{\dfrac {\partial x_{3}}{\partial y}}&{\dfrac {\partial x_{3}}{\partial z}}\end{vmatrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5e5df9134486606d6a55c8ec4a96ee3ca353e924)











![{\displaystyle L^{2}([-\pi,\pi])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0f84fea7a212acaf14649b6cdcca282b0646a8b0)


![{\displaystyle f\in L^{2}([-\pi,\pi])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/74d27747bf5e28fa54e94f218bd9296213ef25c5)








![{\displaystyle [x_{0},x_{0}+P]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3ef79a1b836ec65eacb0d2c73464996d2b7830ba)
![{\displaystyle s_{_{N}}(x)=\sum _{n=-N}^{N}S[n]\ e^{i2\pi {\tfrac {n}{P}}x} ,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b5a3caa42e24c74a3efb0abdf3eb44ad068f7eb5)

![{\displaystyle p_{_{N}}(x)=\sum _{n=-N}^{N}p[n]\ e^{i2\pi {\tfrac {n}{P}}x} .}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ef1c25f3121bf8a28e6ae0a7d00eef1b2953f1dc)





![{\displaystyle (в)S[н]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ffc377764cad3da539424befec0212e920570abe)


![{\displaystyle \left(\sum _{n\neq 0}|S[n]|\right)^{2}\leq \sum _{n\neq 0}{\frac {1}{n^{2}}}\cdot \sum _{n\neq 0}|nS[n]|^{2}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5d7d56e47f74b571fd1be62f2ec4df2276c825f5)


![{\displaystyle n^{2}S[n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/340e0b24995005f3669a865a57edb4035b77ca2d)


![{\displaystyle \sup _{x}|s(x)-s_{_{N}}(x)|\leq \sum _{|n|>N}|S[n]|}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d8225d322a5b676b2b1709c2a636dcd092ff11ec)

![{\displaystyle f(x)=\sum _{n=1}^{\infty }{\frac {1}{n^{2}}}\sin \left[\left(2^{n^{3}}+1\right){\frac {x}{2}}\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a8707621c87adf54eadc1389a9b18497c22a437d)








![{\displaystyle [-P/2,P/2]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/773e3d42ef176524eeb449749ec2bc0a83b5566a)

