Уравнение теплопроводности
This article needs additional citations for verification. (August 2024) |

В математике и физике уравнение теплопроводности представляет собой определенное частное дифференциальное уравнение . Решения уравнения теплопроводности иногда называют калорическими функциями . Теория уравнения теплопроводности была впервые разработана Жозефом Фурье в 1822 году с целью моделирования того, как величина, такая как тепло, распространяется через заданную область. С тех пор уравнение теплопроводности и его варианты были признаны фундаментальными во многих разделах как чистой, так и прикладной математики.
Формулировка уравнения
В математике, если дано открытое подмножество U из R n и подынтервал I из R , говорят, что функция u : U × I → R является решением уравнения теплопроводности , если
где ( x 1 , …, x n , t ) обозначает общую точку области. Обычно t называют «временем», а x 1 , …, x n — «пространственными переменными», даже в абстрактных контекстах, где эти фразы не имеют интуитивного смысла. Совокупность пространственных переменных часто называют просто x . Для любого заданного значения t правая часть уравнения — это лапласиан функции u (⋅, t ) : U → R . Таким образом, уравнение теплопроводности часто записывается более компактно как
В контексте физики и техники, особенно в контексте диффузии через среду, более распространено фиксировать декартову систему координат , а затем рассматривать конкретный случай функции u ( x , y , z , t ) трех пространственных переменных ( x , y , z ) и временной переменной t . Тогда говорят, что u является решением уравнения теплопроводности, если
в котором α — положительный коэффициент, называемый температуропроводностью среды. В дополнение к другим физическим явлениям, это уравнение описывает поток тепла в однородной и изотропной среде, где u ( x , y , z , t ) — температура в точке ( x , y , z ) и время t . Если среда не является однородной и изотропной, то α не будет фиксированным коэффициентом, а будет зависеть от ( x , y , z ) ; уравнение также будет иметь немного иную форму. В физической и инженерной литературе для обозначения лапласиана принято использовать ∇ 2 , а не ∆ .
В математике, а также в физике и технике принято использовать обозначение Ньютона для производных по времени, поэтому оно используется для обозначения ∂u/∂т , поэтому уравнение можно записать
Обратите внимание также, что возможность использовать ∆ или ∇ 2 для обозначения лапласиана без явного указания пространственных переменных является отражением того факта, что лапласиан не зависит от выбора системы координат. В математических терминах можно сказать, что лапласиан «трансляционно и вращательно инвариантен». Фактически, это (грубо говоря) простейший дифференциальный оператор, обладающий этими симметриями. Это можно рассматривать как существенное (и чисто математическое) обоснование использования лапласиана и уравнения теплопроводности при моделировании любых физических явлений, которые являются однородными и изотропными, из которых диффузия тепла является основным примером.
"Константа диффузии" α часто не присутствует в математических исследованиях уравнения теплопроводности, в то время как ее значение может быть очень важным в инженерии. Это не является существенным отличием по следующей причине. Пусть u будет функцией с
Определим новую функцию . Тогда, согласно правилу цепочки , имеем
| ( ⁎ ) |
Таким образом, существует простой способ перевода между решениями уравнения теплопроводности с общим значением α и решениями уравнения теплопроводности с α = 1. Таким образом, для целей математического анализа часто достаточно рассмотреть только случай α = 1 .
Поскольку существует другой вариант определения удовлетворяющего, как в ( ⁎ ) выше, установив . Обратите внимание, что два возможных способа определения новой функции, обсуждаемой здесь, сводятся, в физических терминах, к изменению единицы измерения времени или единицы измерения длины.
Интерпретация
Физическая интерпретация уравнения
Неформально, оператор Лапласа ∆ дает разницу между средним значением функции в окрестности точки и ее значением в этой точке. Таким образом, если u — температура, ∆u сообщает (и насколько) материал, окружающий каждую точку, в среднем горячее или холоднее, чем материал в этой точке.
Согласно второму закону термодинамики , тепло будет перетекать от более горячих тел к соседним более холодным телам пропорционально разнице температур и теплопроводности материалов между ними. Когда тепло втекает в материал (соответственно, из него), его температура увеличивается (соответственно, уменьшается) пропорционально количеству тепла, деленному на количество ( массу ) материала, с коэффициентом пропорциональности, называемым удельной теплоемкостью материала.
В результате объединения этих наблюдений уравнение теплопроводности утверждает, что скорость , с которой материал в точке будет нагреваться (или охлаждаться), пропорциональна тому, насколько горячее (или холоднее) окружающий материал. Коэффициент α в уравнении учитывает теплопроводность, удельную теплоемкость и плотность материала.
Интерпретация уравнения
Первую половину вышеприведенного физического мышления можно представить в математической форме. Ключ в том, что для любого фиксированного x , мы имеем
где u ( x ) ( r ) — функция одной переменной, обозначающая среднее значение u по поверхности сферы радиуса r с центром в точке x ; ее можно определить как
в котором ω n − 1 обозначает площадь поверхности единичного шара в n -мерном евклидовом пространстве. Это формализует приведенное выше утверждение о том, что значение ∆ u в точке x измеряет разницу между значением u ( x ) и значением u в точках, близких к x , в том смысле, что последнее кодируется значениями u ( x ) ( r ) для малых положительных значений r .
Следуя этому наблюдению, можно интерпретировать уравнение теплопроводности как наложение бесконечно малого усреднения функции. При наличии решения уравнения теплопроводности значение u ( x , t + τ) для небольшого положительного значения τ может быть приближено как 1/2 н умножить на среднее значение функции u (⋅, t ) по сфере очень малого радиуса с центром в точке x .
Характер решений
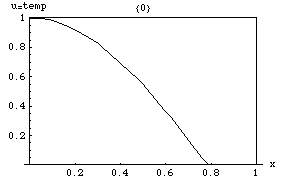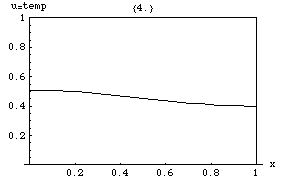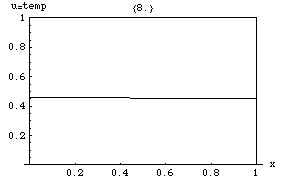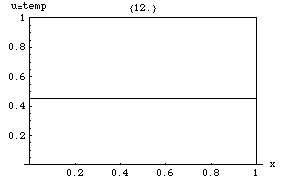

Уравнение теплопроводности подразумевает, что пики ( локальные максимумы ) будут постепенно размываться, в то время как впадины ( локальные минимумы ) будут заполняться. Значение в некоторой точке будет оставаться стабильным только до тех пор, пока оно равно среднему значению в его непосредственном окружении. В частности, если значения в окрестности очень близки к линейной функции , то значение в центре этой окрестности не будет меняться в это время (то есть производная будет равна нулю).
Более тонким следствием является принцип максимума , который гласит, что максимальное значение в любой области среды не превысит максимальное значение, которое ранее имело место в , если только оно не находится на границе . То есть максимальная температура в области может увеличиться только в том случае, если тепло поступает извне . Это свойство параболических уравнений в частных производных и его несложно доказать математически (см. ниже).
Другое интересное свойство заключается в том, что даже если изначально имеет резкий скачок (разрыв) значения на некоторой поверхности внутри среды, скачок немедленно сглаживается мгновенной, бесконечно короткой, но бесконечно большой скоростью потока тепла через эту поверхность. Например, если два изолированных тела, изначально при одинаковой, но разной температуре и , соприкоснуться друг с другом, температура в точке контакта немедленно примет некоторое промежуточное значение, и вокруг этой точки возникнет зона, где будет постепенно меняться между и .
Если к точке среды внезапно приложить определенное количество тепла, оно распространится во всех направлениях в виде диффузионной волны. В отличие от упругих и электромагнитных волн , скорость диффузионной волны со временем падает: по мере распространения на большую область градиент температуры уменьшается, и, следовательно, уменьшается и тепловой поток.
Конкретные примеры
Тепловой поток в однородном стержне
Для теплового потока уравнение теплопроводности следует из физических законов теплопроводности и сохранения энергии (Кэннон, 1984).
По закону Фурье для изотропной среды скорость потока тепловой энергии на единицу площади через поверхность пропорциональна отрицательному градиенту температуры на ней:
где — теплопроводность материала, — температура, а — векторное поле, представляющее величину и направление теплового потока в точке пространства и времени .
Если среда представляет собой тонкий стержень однородного сечения и материала, то положение x является единственной координатой, а поток тепла в направлении является скалярным полем . Уравнение становится
Пусть будет внутренней энергией (теплом) на единицу объема стержня в каждой точке и времени. Скорость изменения тепла на единицу объема в материале, , пропорциональна скорости изменения его температуры, . То есть,
где — удельная теплоемкость (при постоянном давлении, в случае газа), а — плотность (масса на единицу объема) материала. Этот вывод предполагает, что материал имеет постоянную плотность массы и теплоемкость как в пространстве, так и во времени.
Применяя закон сохранения энергии к малому элементу среды с центром в точке , можно прийти к выводу, что скорость изменения тепла в данной точке равна производной теплового потока в этой точке (разнице между тепловыми потоками по обе стороны от частицы). То есть,
Из приведенных выше уравнений следует, что
что является уравнением теплопроводности в одном измерении с коэффициентом диффузии
Эта величина называется температуропроводностью среды.
Учет радиационных потерь
Дополнительный член может быть введен в уравнение для учета лучистой потери тепла. Согласно закону Стефана-Больцмана , этот член равен , где - температура окружающей среды, а - коэффициент, зависящий от постоянной Стефана-Больцмана и излучательной способности материала. Скорость изменения внутренней энергии становится
и уравнение для эволюции становится
Неоднородная изотропная среда
Обратите внимание, что уравнение состояния, заданное первым законом термодинамики (т.е. сохранением энергии), записывается в следующей форме (предполагая отсутствие переноса массы или излучения). Эта форма является более общей и особенно полезна для распознавания того, какое свойство (например, c p или ) влияет на какой член.
где - объемный источник тепла.
Трехмерная задача
В частных случаях распространения тепла в изотропной и однородной среде в трехмерном пространстве это уравнение имеет вид
где:
- температура как функция пространства и времени;
- скорость изменения температуры в точке с течением времени;
- , , и — вторые пространственные производные ( коэффициенты теплопроводности ) температуры в направлениях , , и соответственно;
- — температуропроводность , величина, зависящая от материала и зависящая от теплопроводности , удельной теплоемкости и плотности массы .
Уравнение теплопроводности является следствием закона Фурье (см. теплопроводность ).
Если среда не является всем пространством, то для однозначного решения уравнения теплопроводности нам также необходимо указать граничные условия для u . Для определения единственности решений во всем пространстве необходимо предположить дополнительные условия, например, экспоненциальную границу роста решений [1] или знаковое условие (неотрицательные решения единственны согласно результату Дэвида Виддера ). [2]
Решения уравнения теплопроводности характеризуются постепенным сглаживанием начального распределения температуры потоком тепла от более теплых к более холодным областям объекта. Как правило, множество различных состояний и начальных условий будут стремиться к одному и тому же устойчивому равновесию . Как следствие, обращение решения и заключение чего-либо о более ранних временах или начальных условиях из текущего распределения тепла очень неточно, за исключением самых коротких периодов времени.
Уравнение теплопроводности является типичным примером параболического уравнения в частных производных .
Используя оператор Лапласа , уравнение теплопроводности можно упростить и обобщить до аналогичных уравнений в пространствах произвольного числа измерений, как
где оператор Лапласа, Δ или ∇ 2 , дивергенция градиента, берется в пространственных переменных.
Уравнение теплопроводности управляет диффузией тепла, а также другими диффузионными процессами, такими как диффузия частиц или распространение потенциала действия в нервных клетках. Хотя они не являются диффузионными по своей природе, некоторые проблемы квантовой механики также управляются математическим аналогом уравнения теплопроводности (см. ниже). Его также можно использовать для моделирования некоторых явлений, возникающих в финансах , таких как процессы Блэка-Шоулза или Орнштейна-Уленбека . Уравнение и различные нелинейные аналоги также использовались в анализе изображений.
Уравнение теплопроводности, технически, нарушает специальную теорию относительности , поскольку его решения включают мгновенное распространение возмущения. Часть возмущения за пределами переднего светового конуса обычно можно безопасно пренебречь, но если необходимо развить разумную скорость для передачи тепла, вместо этого следует рассмотреть гиперболическую задачу — например, уравнение в частных производных, включающее производную по времени второго порядка. Некоторые модели нелинейной теплопроводности (которые также являются параболическими уравнениями) имеют решения с конечной скоростью передачи тепла. [3] [4]
Внутреннее тепловыделение
Функция u выше представляет температуру тела. В качестве альтернативы иногда удобно изменить единицы и представить u как плотность тепла среды. Поскольку плотность тепла пропорциональна температуре в однородной среде, уравнение теплопроводности по-прежнему соблюдается в новых единицах.
Предположим, что тело подчиняется уравнению теплопроводности и, кроме того, генерирует собственное тепло на единицу объема (например, в ваттах/литр - Вт/л) со скоростью, заданной известной функцией q, изменяющейся в пространстве и времени. [5] Тогда тепло на единицу объема u удовлетворяет уравнению
Например, нить накаливания вольфрамовой лампочки генерирует тепло, поэтому при включении она будет иметь положительное ненулевое значение q . Пока свет выключен, значение q для вольфрамовой нити будет равно нулю.
Решение уравнения теплопроводности с использованием ряда Фурье

Следующий метод решения уравнения теплопроводности был предложен Жозефом Фурье в его трактате Théorie analytique de la chaleur , опубликованном в 1822 году. Рассмотрим уравнение теплопроводности для одной пространственной переменной. Это можно использовать для моделирования теплопроводности в стержне. Уравнение имеет вид
| ( 1 ) |
где u = u ( x , t ) — функция двух переменных x и t . Здесь
- x — пространственная переменная, поэтому x ∈ [0, L ], где L — длина стержня.
- t — переменная времени, поэтому t ≥ 0.
Примем начальное условие
| ( 2 ) |
где функция f задана, а граничные условия
| . | ( 3 ) |
Попытаемся найти решение уравнения ( 1 ), которое не является тождественно нулевым, удовлетворяющим граничным условиям ( 3 ), но обладает следующим свойством: u — произведение, в котором зависимость u от x , t разделена, то есть:
| ( 4 ) |
Этот метод решения называется разделением переменных . Подставляя u обратно в уравнение ( 1 ),
Поскольку правая часть зависит только от x , а левая часть только от t , обе стороны равны некоторой постоянной величине − λ . Таким образом:
| ( 5 ) |
и
| ( 6 ) |
Теперь покажем, что нетривиальные решения для ( 6 ) при значениях λ ≤ 0 не могут возникнуть:
- Предположим, что λ < 0. Тогда существуют действительные числа B , C , такие что Из ( 3 ) получаем X (0) = 0 = X ( L ) и, следовательно, B = 0 = C, что означает, что u тождественно равно 0.
- Предположим, что λ = 0. Тогда существуют действительные числа B , C, такие, что X ( x ) = Bx + C. Из уравнения ( 3 ) заключаем так же, как и в 1, что u тождественно равно 0.
- Следовательно, должно быть так, что λ > 0. Тогда существуют действительные числа A , B , C, такие, что и Из ( 3 ) получаем C = 0 и что для некоторого положительного целого числа n ,
Это решает уравнение теплопроводности в частном случае, когда зависимость u имеет специальный вид ( 4 ).
В общем случае сумма решений ( 1 ), удовлетворяющих граничным условиям ( 3 ), также удовлетворяет ( 1 ) и ( 3 ). Мы можем показать, что решение ( 1 ), ( 2 ) и ( 3 ) задается как
где
Обобщение метода решения
Метод решения, использованный выше, может быть значительно расширен на многие другие типы уравнений. Идея состоит в том, что оператор u xx с нулевыми граничными условиями может быть представлен в терминах его собственных функций . Это естественным образом приводит к одной из основных идей спектральной теории линейных самосопряженных операторов .
Рассмотрим линейный оператор Δ u = u xx . Бесконечная последовательность функций
для n ≥ 1 являются собственными функциями Δ. Действительно,
Более того, любая собственная функция f оператора Δ с граничными условиями f (0) = f ( L ) = 0 имеет вид e n для некоторого n ≥ 1. Функции e n для n ≥ 1 образуют ортонормированную последовательность относительно некоторого скалярного произведения на пространстве действительнозначных функций на [0, L ]. Это означает
Наконец, последовательность { e n } n ∈ N охватывает плотное линейное подпространство L 2 ((0, L )). Это показывает, что по сути мы диагонализировали оператор Δ.
Теплопроводность в неоднородных анизотропных средах
В целом, изучение теплопроводности основано на нескольких принципах. Тепловой поток является формой потока энергии , и поэтому имеет смысл говорить о скорости потока тепла в область пространства.
- Скорость потока тепла в область V определяется зависящей от времени величиной q t ( V ). Мы предполагаем, что q имеет плотность Q , так что
- Тепловой поток — это векторная функция, зависящая от времени H ( x ), которая характеризуется следующим образом: скорость потока тепла через бесконечно малый элемент поверхности площадью dS и единичным вектором нормали n равна Таким образом, скорость потока тепла в V также определяется поверхностным интегралом , где n ( x ) — вектор нормали, направленный наружу в точке x .
- Закон Фурье гласит, что поток тепловой энергии имеет следующую линейную зависимость от градиента температуры , где A ( x ) — действительная матрица размером 3 × 3 , которая является симметричной и положительно определенной .
- По теореме о расходимости предыдущий поверхностный интеграл для теплового потока в V можно преобразовать в объемный интеграл
- Скорость изменения температуры в точке x пропорциональна теплу, поступающему в бесконечно малый элемент объема, где коэффициент пропорциональности зависит от константы κ
Объединив эти уравнения, получаем общее уравнение теплового потока:
Замечания
- Коэффициент κ ( x ) является величиной, обратной произведению удельной теплоемкости вещества при x на плотность вещества при x : .
- В случае изотропной среды матрица A представляет собой скалярную матрицу, равную теплопроводности k .
- В анизотропном случае, когда матрица коэффициентов A не является скалярной и/или зависит от x , то явную формулу для решения уравнения теплопроводности редко можно записать, хотя обычно можно рассмотреть связанную абстрактную задачу Коши и показать, что это корректно поставленная задача и/или показать некоторые качественные свойства (такие как сохранение положительных начальных данных, бесконечная скорость распространения, сходимость к равновесию, сглаживающие свойства). Обычно это делается с помощью теории однопараметрических полугрупп : например, если A — симметричная матрица, то эллиптический оператор, определяемый как , является самосопряженным и диссипативным, таким образом, по спектральной теореме он порождает однопараметрическую полугруппу .
Фундаментальные решения
Фундаментальное решение , также называемое тепловым ядром , является решением уравнения теплопроводности, соответствующим начальному состоянию исходного точечного источника тепла в известном положении. Их можно использовать для нахождения общего решения уравнения теплопроводности в определенных областях; см., например, (Evans 2010) для вводного рассмотрения.
При одной переменной функция Грина является решением задачи начального значения (по принципу Дюамеля , что эквивалентно определению функции Грина как функции с дельта-функцией в качестве решения первого уравнения)
где - дельта-функция Дирака . Решение этой задачи - фундаментальное решение ( тепловое ядро )
Общее решение уравнения теплопроводности с одной переменной и начальным условием u ( x , 0) = g ( x ) для −∞ < x < ∞ и 0 < t < ∞ можно получить, применив свертку :
В нескольких пространственных переменных фундаментальное решение решает аналогичную задачу
Фундаментальное решение для n переменных является произведением фундаментальных решений по каждой переменной, т.е.
Общее решение уравнения теплопроводности на R n затем получается с помощью свертки, так что для решения задачи начального значения с u ( x , 0) = g ( x ) необходимо
Общая задача на области Ω в R n имеет вид
с граничными данными Дирихле или Неймана . Функция Грина всегда существует, но если область Ω не может быть легко разложена на задачи с одной переменной (см. ниже), ее может быть невозможно явно записать. Другие методы получения функций Грина включают метод изображений , разделение переменных и преобразования Лапласа (Cole, 2011).
Некоторые решения функции Грина в 1D
Здесь записаны различные элементарные решения функции Грина в одном измерении; многие другие доступны в других местах. [6] В некоторых из них пространственная область — это (−∞,∞). В других — это полубесконечный интервал (0,∞) с граничными условиями Неймана или Дирихле . Еще одно изменение заключается в том, что некоторые из них решают неоднородное уравнение
где f — некоторая заданная функция x и t .
Однородное уравнение теплопроводности
- Начальная задача на (−∞,∞)

Комментарий . Это решение является сверткой по переменной x фундаментального решения
и функция g ( x ). ( Число функции Грина фундаментального решения равно X00.)
Следовательно, согласно общим свойствам свертки относительно дифференцирования, u = g ∗ Φ является решением того же уравнения теплопроводности, для
Более того,
так что, по общим фактам о приближении к тождеству , Φ(⋅, t ) ∗ g → g при t → 0 в различных смыслах, в соответствии с конкретным g . Например, если g предполагается ограниченным и непрерывным на R, то Φ(⋅, t ) ∗ g равномерно сходится к g при t → 0, что означает, что u ( x , t ) непрерывен на R × [0, ∞) с u ( x , 0) = g ( x ).
- Начальная задача на (0,∞) с однородными граничными условиями Дирихле
Комментарий. Это решение получено из предыдущей формулы, примененной к данным g ( x ), соответствующим образом расширенным на R , так, чтобы быть нечетной функцией , то есть, полагая g (− x ) := − g ( x ) для всех x . Соответственно, решение начальной задачи на (−∞,∞) является нечетной функцией относительно переменной x для всех значений t , и в частности оно удовлетворяет однородным граничным условиям Дирихле u (0, t ) = 0. Число функции Грина этого решения равно X10.
- Начальная задача на (0,∞) с однородными граничными условиями Неймана
Комментарий. Это решение получено из первой формулы решения, примененной к данным g ( x ), соответствующим образом расширенным на R так, чтобы быть четной функцией , то есть, полагая g (− x ) := g ( x ) для всех x . Соответственно, решение начальной задачи на R является четной функцией относительно переменной x для всех значений t > 0, и, в частности, будучи гладким, оно удовлетворяет однородным граничным условиям Неймана u x (0, t ) = 0. Число функции Грина этого решения равно X20.
- Задача на (0,∞) с однородными начальными условиями и неоднородными граничными условиями Дирихле
Комментарий . Это решение представляет собой свертку по переменной t
и функция h ( t ). Поскольку Φ( x , t ) является фундаментальным решением
функция ψ ( x , t ) также является решением того же уравнения теплопроводности, как и u := ψ ∗ h , благодаря общим свойствам свертки относительно дифференцирования. Более того,
так что, по общим фактам о приближении к тождеству , ψ ( x , ⋅) ∗ h → h при x → 0 в различных смыслах, в соответствии с конкретным h . Например, если h предполагается непрерывным на R с носителем в [0, ∞), то ψ ( x , ⋅) ∗ h сходится равномерно на компактах к h при x → 0, что означает, что u ( x , t ) непрерывен на [0, ∞) × [0, ∞) с u (0, t ) = h ( t ).

Неоднородное уравнение теплопроводности
- Задача на (-∞,∞) однородные начальные условия
Комментарий . Это решение является сверткой в R 2 , то есть по обеим переменным x и t , фундаментального решения
и функция f ( x , t ), обе подразумеваются определенными на всем R 2 и тождественно равными 0 для всех t → 0. Проверяется, что
что выражается на языке распределений становится
где распределение δ — это дельта-функция Дирака , то есть оценка при 0.
- Задача на (0,∞) с однородными граничными условиями Дирихле и начальными условиями
Комментарий . Это решение получается из предыдущей формулы, примененной к данным f ( x , t ) соответствующим образом расширенным на R × [0,∞), так чтобы быть нечетной функцией переменной x , то есть, полагая f (− x , t ) := − f ( x , t ) для всех x и t . Соответственно, решение неоднородной задачи на (−∞,∞) является нечетной функцией относительно переменной x для всех значений t , и в частности оно удовлетворяет однородным граничным условиям Дирихле u (0, t ) = 0.
- Задача на (0,∞) с однородными граничными условиями Неймана и начальными условиями
Комментарий . Это решение получается из первой формулы, примененной к данным f ( x , t ) соответствующим образом расширенным на R × [0,∞), так, чтобы быть четной функцией переменной x , то есть, полагая f (− x , t ) := f ( x , t ) для всех x и t . Соответственно, решение неоднородной задачи на (−∞,∞) является четной функцией относительно переменной x для всех значений t , и, в частности, будучи гладкой функцией, она удовлетворяет однородным граничным условиям Неймана u x (0, t ) = 0.
Примеры
Поскольку уравнение теплопроводности является линейным, решения других комбинаций граничных условий, неоднородного члена и начальных условий можно найти, взяв соответствующую линейную комбинацию приведенных выше решений функции Грина.
Например, чтобы решить
пусть u = w + v , где w и v решают задачи
Аналогично, чтобы решить
пусть u = w + v + r, где w , v и r решают задачи
Свойство среднего значения для уравнения теплопроводности
Решения уравнений теплопроводности
удовлетворяют свойству среднего значения, аналогичному свойствам среднего значения гармонических функций , решения
хотя немного сложнее. Точно, если вы решите
и
затем
где E λ — «тепловой шар», то есть множество сверхуровней фундаментального решения уравнения теплопроводности:
Обратите внимание, что
при λ → ∞, поэтому приведенная выше формула верна для любого ( x , t ) в (открытом) множестве dom( u ) для достаточно большого λ . [7] Это можно показать с помощью рассуждения, аналогичного аналогичному для гармонических функций .
Уравнение стационарного тепла
Уравнение стационарного тепла по определению не зависит от времени. Другими словами, предполагается, что существуют такие условия, что:
Это условие зависит от постоянной времени и количества времени, прошедшего с момента наложения граничных условий. Таким образом, условие выполняется в ситуациях, в которых постоянная времени равновесия достаточно быстра , чтобы более сложное зависящее от времени уравнение теплопроводности можно было аппроксимировать стационарным случаем. Эквивалентно, стационарное условие существует для всех случаев, в которых прошло достаточно времени , чтобы тепловое поле u больше не эволюционировало во времени.
В стационарном случае пространственный температурный градиент может (или не может) существовать, но если он есть, он не меняется со временем. Таким образом, это уравнение описывает конечный результат во всех тепловых задачах, в которых включается источник (например, запускается двигатель автомобиля), и проходит достаточно времени для того, чтобы все постоянные температурные градиенты установились в пространстве, после чего эти пространственные градиенты больше не меняются со временем (как снова в случае с автомобилем, в котором двигатель работает достаточно долго). Другое (тривиальное) решение заключается в том, чтобы все пространственные температурные градиенты также исчезли, и в этом случае температура также становится однородной в пространстве.
Уравнение намного проще и может помочь лучше понять физику материалов, не сосредотачиваясь на динамике процесса переноса тепла. Оно широко используется для простых инженерных задач, предполагая, что существует равновесие температурных полей и переноса тепла со временем.
Устойчивое состояние:
Уравнение стационарного теплообмена для объема, содержащего источник тепла (неоднородный случай), представляет собой уравнение Пуассона :
где u — температура , k — теплопроводность , q — скорость выделения тепла в единице объема.
В электростатике это эквивалентно случаю, когда рассматриваемое пространство содержит электрический заряд.
Уравнение стационарной теплопроводности без источника тепла внутри объема (однородный случай) — это уравнение электростатики для объема свободного пространства, не содержащего заряда. Оно описывается уравнением Лапласа :
Приложения
Как прототип параболического уравнения в частных производных , уравнение теплопроводности является одной из наиболее широко изучаемых тем в чистой математике , и его анализ считается фундаментальным для более широкой области уравнений в частных производных . Уравнение теплопроводности также можно рассматривать на римановых многообразиях , что приводит к многочисленным геометрическим приложениям. После работы Суббарамайи Минакшисундарама и Оке Плейеля уравнение теплопроводности тесно связано со спектральной геометрией . Основополагающий нелинейный вариант уравнения теплопроводности был введен в дифференциальную геометрию Джеймсом Иллсом и Джозефом Сэмпсоном в 1964 году, что вдохновило Ричарда Гамильтона на введение потока Риччи в 1982 году и достигло кульминации в доказательстве гипотезы Пуанкаре Григорием Перельманом в 2003 году. Некоторые решения уравнения теплопроводности, известные как ядра теплопроводности, предоставляют тонкую информацию об области, в которой они определены, как показано на примере их применения к теореме об индексе Атьи–Зингера . [8]
Уравнение теплопроводности, вместе с его вариантами, также важно во многих областях науки и прикладной математики . В теории вероятностей уравнение теплопроводности связано с изучением случайных блужданий и броуновского движения через уравнение Фоккера–Планка . Уравнение Блэка–Шоулза финансовой математики является небольшим вариантом уравнения теплопроводности, а уравнение Шредингера квантовой механики можно рассматривать как уравнение теплопроводности в мнимом времени . В анализе изображений уравнение теплопроводности иногда используется для разрешения пикселизации и идентификации краев . После введения Робертом Рихтмайером и Джоном фон Нейманом методов «искусственной вязкости» решения уравнений теплопроводности стали полезными в математической формулировке гидродинамических ударов . Решениям уравнения теплопроводности также уделялось большое внимание в литературе по численному анализу , начиная с 1950-х годов с работы Джима Дугласа, Д. В. Писмана и Генри Рачфорда-младшего.
Диффузия частиц
Диффузию частиц можно моделировать с помощью уравнения, включающего:
- объемная концентрация частиц, обозначаемая c , в случае коллективной диффузии большого числа частиц, или
- функция плотности вероятности , связанная с положением отдельной частицы, обозначается P.
В любом случае используется уравнение теплопроводности
или
И c, и P являются функциями положения и времени. D — коэффициент диффузии, который контролирует скорость диффузионного процесса и обычно выражается в метрах в квадрате за секунду. Если коэффициент диффузии D не является постоянным, а зависит от концентрации c (или P во втором случае), то получается нелинейное уравнение диффузии .
Броуновское движение
Пусть случайный процесс является решением стохастического дифференциального уравнения
где - процесс Винера (стандартное броуновское движение). Функция плотности вероятности в любой момент времени задается выражением
что является решением задачи начального значения
где — дельта-функция Дирака .
Уравнение Шредингера для свободной частицы
С помощью простого деления уравнение Шредингера для одной частицы массой m при отсутствии какого-либо приложенного силового поля можно переписать следующим образом:
- ,
где i — мнимая единица , ħ — приведенная постоянная Планка , а ψ — волновая функция частицы.
Это уравнение формально аналогично уравнению диффузии частиц, которое получается путем следующего преобразования:
Применение этого преобразования к выражениям функций Грина, определенных в случае диффузии частиц, дает функции Грина уравнения Шредингера , которые, в свою очередь, можно использовать для получения волновой функции в любой момент времени через интеграл по волновой функции при t = 0:
с
Замечание: эта аналогия между квантовой механикой и диффузией является чисто формальной. Физически эволюция волновой функции, удовлетворяющей уравнению Шредингера, может иметь иное происхождение, чем диффузия [ требуется цитата ] .
Температуропроводность в полимерах
Прямое практическое применение уравнения теплопроводности в сочетании с теорией Фурье в сферических координатах — это прогнозирование профилей теплопередачи и измерение температуропроводности в полимерах ( Ансворт и Дуарте ). Этот двойной теоретико-экспериментальный метод применим к резине, различным другим полимерным материалам, представляющим практический интерес, и микрожидкостям. Эти авторы вывели выражение для температуры в центре сферы T C
где T 0 — начальная температура сферы, а T S — температура на поверхности сферы радиусом L. Это уравнение также нашло применение в переносе энергии белками и тепловом моделировании в биофизике.
Применение в различных областях
Уравнение теплопроводности возникает при моделировании ряда явлений и часто используется в финансовой математике при моделировании опционов . Дифференциальное уравнение модели ценообразования опционов Блэка-Шоулза можно преобразовать в уравнение теплопроводности, допускающее относительно простые решения из знакомого корпуса математики. Многие расширения простых моделей опционов не имеют решений в замкнутой форме и, таким образом, должны быть решены численно для получения смоделированной цены опциона. Уравнение, описывающее диффузию давления в пористой среде, по форме идентично уравнению теплопроводности. Задачи диффузии, связанные с граничными условиями Дирихле , Неймана и Робина , имеют аналитические решения в замкнутой форме (Thambynayagam 2011). Уравнение теплопроводности также широко используется в анализе изображений (Perona & Malik 1990) и в машинном обучении в качестве движущей теории, лежащей в основе методов масштабного пространства или графа Лапласа . Уравнение теплопроводности можно эффективно решить численно с использованием неявного метода Кранка-Николсона (Crank & Nicolson 1947). Этот метод можно распространить на многие модели, не имеющие решения в замкнутой форме, см., например, (Wilmott, Howison & Dewynne 1995).
Абстрактная форма уравнения теплопроводности на многообразиях обеспечивает основной подход к теореме Атьи–Зингера об индексе и привела к значительному дальнейшему исследованию уравнений теплопроводности в римановой геометрии .
Смотрите также
- Калорический полином
- Поток, сокращающий кривую
- Уравнение диффузии
- Релятивистская теплопроводность
- Уравнение Шредингера
- преобразование Вейерштрасса
Примечания
- ^ Стоянович, Срджан (2003), «3.3.1.3 Уникальность для теплового уравнения в частных производных с экспоненциальным ростом на бесконечности», Вычислительная финансовая математика с использованием MATHEMATICA®: Оптимальная торговля акциями и опционами, Springer, стр. 112–114, ISBN 9780817641979
- ^ Джон, Фриц (1991-11-20). Уравнения с частными производными. Springer Science & Business Media. стр. 222. ISBN 978-0-387-90609-6.
- ^ Mathworld: Уравнение пористой среды и другие связанные модели имеют решения с конечной скоростью распространения волн.
- ^ Хуан Луис Васкес (28.12.2006), Уравнение пористой среды: математическая теория , Oxford University Press, США, ISBN 978-0-19-856903-9
- ^ Обратите внимание, что единицы измерения u должны быть выбраны таким образом, чтобы они были совместимы с единицами измерения q . Таким образом, вместо единиц измерения термодинамической температуры ( Кельвин - К) единицами измерения u должны быть Дж/Л.
- ^ Библиотека функций Грина содержит множество фундаментальных решений уравнения теплопроводности.
- ^ Наоборот, любая функция u, удовлетворяющая указанному выше свойству среднего значения на открытой области R n × R, является решением уравнения теплопроводности
- ^ Берлин, Николь; Гетцлер, Эзра; Вернь, Мишель. Тепловые ядра и операторы Дирака. Grundlehren der Mathematischen Wissenschaften, 298. Springer-Verlag, Берлин, 1992. viii+369 стр. ISBN 3-540-53340-0
Ссылки
- Кэннон, Джон Розье (1984), Одномерное уравнение теплопроводности , Энциклопедия математики и ее приложений, т. 23, Рединг, Массачусетс: Addison-Wesley Publishing Company, Расширенная программа книг, ISBN 0-201-13522-1, MR 0747979, Zbl 0567.35001
- Crank, J.; Nicolson, P. (1947), "Практический метод численной оценки решений уравнений с частными производными типа теплопроводности", Труды Кембриджского философского общества , 43 (1): 50–67, Bibcode : 1947PCPS...43...50C, doi : 10.1017/S0305004100023197, S2CID 16676040
- Эванс, Лоуренс К. (2010), Уравнения с частными производными, Graduate Studies in Mathematics, т. 19 (2-е изд.), Провиденс, Род-Айленд: Американское математическое общество, ISBN 978-0-8218-4974-3
- Перона, П.; Малик, Дж. (1990), «Обнаружение масштабного пространства и границ с использованием анизотропной диффузии» (PDF) , Труды IEEE по анализу образов и машинному интеллекту , 12 (7): 629–639, doi :10.1109/34.56205, S2CID 14502908
- Тамбинаягам, РКМ (2011), Справочник по диффузии: прикладные решения для инженеров , McGraw-Hill Professional, ISBN 978-0-07-175184-1
- Уилмотт, Пол; Хоуисон, Сэм; Дьюинн, Джефф (1995), Математика финансовых производных. Введение для студентов , Кембридж: Cambridge University Press, ISBN 0-521-49699-3
Дальнейшее чтение
- Карслоу, Х.С.; Джегер, Дж.К. (1988), Теплопроводность в твердых телах , Oxford Science Publications (2-е изд.), Нью-Йорк: The Clarendon Press, Oxford University Press, ISBN 978-0-19-853368-9
- Коул, Кевин Д.; Бек, Джеймс В.; Хаджи-Шейх, А.; Литкухи, Бахан (2011), Теплопроводность с использованием функций Грина , Серия вычислительных и физических процессов в механике и тепловых науках (2-е изд.), Бока-Ратон, Флорида: CRC Press, ISBN 978-1-43-981354-6
- Эйнштейн, Альберт (1905), «Über die von der molekularkinetischen Theorie der Wärme geforderte Bewegung von in ruhenden Flüssigkeiten suspendierten Teilchen» (PDF) , Annalen der Physik , 322 (8): 549–560, Бибкод : 1905AnP...322. .549E, doi : 10.1002/andp.19053220806
- Фридман, Авнер (1964), Уравнения с частными производными параболического типа , Энглвуд Клиффс, Нью-Джерси: Prentice-Hall
- Ансворт, Дж.; Дуарте, Ф.Дж. (1979), «Диффузия тепла в твердой сфере и теория Фурье», Am. J. Phys. , 47 (11): 891–893, Bibcode : 1979AmJPh..47..981U, doi : 10.1119/1.11601
- Джили, Латиф М. (2009), Теплопроводность , Springer (3-е изд.), Берлин-Гейдельберг: Springer-Verlag, ISBN 978-3-642-01266-2
- Виддер, Д.В. (1975), Уравнение теплопроводности , Чистая и прикладная математика, т. 67, Нью-Йорк-Лондон: Academic Press [издательство Harcourt Brace Jovanovich]
Внешние ссылки
- Вывод уравнения теплопроводности
- Линейные уравнения теплопроводности: частные решения и краевые задачи - от EqWorld
- «Уравнение тепла». PBS Infinite Series . 17 ноября 2017 г. Архивировано из оригинала 2021-12-11 – через YouTube .



























































![{\displaystyle u(x,0)=f(x)\quad \forall x\in [0,L]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d131258344a404f634278886f71177e367fe1ca4)





































![{\displaystyle \left(\partial _{t}-k\partial _{x}^{2}\right)(\Phi *g)=\left[\left(\partial _{t}-k\partial _{x}^{2}\right)\Phi \right]*g=0.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a86fafd32ba64a9d2a7d89291dceec95a9eac19f)



![{\displaystyle u(x,t)={\frac {1}{\sqrt {4\pi kt}}}\int _{0}^{\infty }\left[\exp \left(-{\frac {(xy)^{2}}{4kt}}\right)-\exp \left(-{\frac {(x+y)^{2}}{4kt}}\right)\right]g(y)\,dy}](https://wikimedia.org/api/rest_v1/media/math/render/svg/aee16fc53676947cca80b307666072f431c80417)

![{\displaystyle u(x,t)={\frac {1}{\sqrt {4\pi kt}}}\int _{0}^{\infty }\left[\exp \left(-{\frac {(xy)^{2}}{4kt}}\right)+\exp \left(-{\frac {(x+y)^{2}}{4kt}}\right)\right]g(y)\,dy}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0c0f51e3157b5995f0357306e5904aad683ee429)








































