Диэлектрик

| Статьи о |
| Электромагнетизм |
|---|
 |
В электромагнетизме диэлектрик (или диэлектрическая среда ) — это электрический изолятор , который может быть поляризован приложенным электрическим полем . Когда диэлектрический материал помещается в электрическое поле, электрические заряды не текут через материал, как в электрическом проводнике , потому что у них нет слабо связанных или свободных электронов, которые могут дрейфовать через материал, но вместо этого они смещаются, лишь немного, от своих средних положений равновесия, вызывая диэлектрическую поляризацию . Из-за диэлектрической поляризации положительные заряды смещаются в направлении поля, а отрицательные заряды смещаются в направлении, противоположном полю. Это создает внутреннее электрическое поле, которое уменьшает общее поле внутри самого диэлектрика. Если диэлектрик состоит из слабо связанных молекул, эти молекулы не только поляризуются, но и переориентируются так, что их оси симметрии выстраиваются в соответствии с полем. [1]
Изучение диэлектрических свойств касается хранения и рассеивания электрической и магнитной энергии в материалах. [2] [3] [4] Диэлектрики важны для объяснения различных явлений в электронике , оптике , физике твердого тела и клеточной биофизике . [5] [6]
Терминология
Хотя термин изолятор подразумевает низкую электропроводность , диэлектрик обычно означает материалы с высокой поляризуемостью . Последняя выражается числом, называемым относительной диэлектрической проницаемостью . Изолятор обычно используется для обозначения электрического препятствия, в то время как диэлектрик используется для обозначения способности материала накапливать энергию (посредством поляризации). Распространенным примером диэлектрика является электроизолирующий материал между металлическими пластинами конденсатора . Поляризация диэлектрика приложенным электрическим полем увеличивает поверхностный заряд конденсатора для данной напряженности электрического поля. [1]
Термин «диэлектрик» был придуман Уильямом Уэвеллом (от dia + electric ) в ответ на просьбу Майкла Фарадея . [7] [8]
Идеальный диэлектрик — это материал с нулевой электропроводностью ( ср. идеальный проводник с бесконечной электропроводностью) [9] , таким образом, демонстрирующий только ток смещения ; поэтому он хранит и возвращает электрическую энергию, как если бы он был идеальным конденсатором.
Электрическая восприимчивость
Электрическая восприимчивость диэлектрического материала является мерой того, насколько легко он поляризуется в ответ на электрическое поле. Это, в свою очередь, определяет электрическую проницаемость материала и, таким образом, влияет на многие другие явления в этой среде, от емкости конденсаторов до скорости света .
Он определяется как константа пропорциональности (которая может быть тензором ), связывающая электрическое поле с плотностью индуцированной диэлектрической поляризации, такой что
где - электрическая диэлектрическая проницаемость свободного пространства .
Восприимчивость среды связана с ее относительной диэлектрической проницаемостью соотношением
Так в случае классического вакуума ,
Электрическое смещение связано с плотностью поляризации соотношением
Дисперсия и причинность
В общем, материал не может поляризоваться мгновенно в ответ на приложенное поле. Более общая формулировка как функция времени:
То есть поляризация представляет собой свертку электрического поля в предыдущие моменты времени с восприимчивостью, зависящей от времени, заданной как . Верхний предел этого интеграла можно расширить до бесконечности, если определить для . Мгновенный отклик соответствует восприимчивости дельта-функции Дирака .
В линейной системе удобнее взять преобразование Фурье и записать это соотношение как функцию частоты. Благодаря теореме о свертке интеграл становится простым произведением,
Восприимчивость (или, что то же самое, диэлектрическая проницаемость) зависит от частоты. Изменение восприимчивости в зависимости от частоты характеризует дисперсионные свойства материала.
Более того, тот факт, что поляризация может зависеть только от электрического поля в предыдущие моменты времени (т.е. для ), как следствие причинности , накладывает ограничения Крамерса-Кронига на действительную и мнимую части восприимчивости .
Диэлектрическая поляризация
Базовая модель атома

В классическом подходе к диэлектрику материал состоит из атомов. Каждый атом состоит из облака отрицательного заряда (электронов), связанного с положительным точечным зарядом в его центре и окружающего его. В присутствии электрического поля облако заряда искажается, как показано в правом верхнем углу рисунка.
Это можно свести к простому диполю , используя принцип суперпозиции . Диполь характеризуется своим дипольным моментом , векторной величиной, показанной на рисунке синей стрелкой с надписью M. Именно соотношение между электрическим полем и дипольным моментом обуславливает поведение диэлектрика. (Обратите внимание, что дипольный момент указывает в том же направлении, что и электрическое поле на рисунке. Это не всегда так и является большим упрощением, но справедливо для многих материалов.)
При удалении электрического поля атом возвращается в исходное состояние. Время, необходимое для этого, называется временем релаксации ; экспоненциальный распад.
Это суть модели в физике. Поведение диэлектрика теперь зависит от ситуации. Чем сложнее ситуация, тем богаче должна быть модель, чтобы точно описать поведение. Важные вопросы:
- Постоянно ли электрическое поле или оно меняется со временем? С какой скоростью?
- Зависит ли реакция от направления приложенного поля ( изотропия материала)?
- Везде ли реакция одинакова ( однородность материала)?
- Необходимо ли учитывать какие-либо границы или интерфейсы?
- Является ли реакция линейной относительно поля или имеются нелинейности ?
Связь между электрическим полем E и дипольным моментом M обуславливает поведение диэлектрика, которое для данного материала можно охарактеризовать функцией F, определяемой уравнением:
Когда определены и тип электрического поля, и тип материала, выбирается простейшая функция F , которая правильно предсказывает интересующие вас явления. Примеры явлений, которые можно смоделировать таким образом, включают:
- Показатель преломления
- Дисперсия групповой скорости
- Двойное лучепреломление
- Самофокусирующийся
- Генерация гармоник
Дипольная поляризация
Дипольная поляризация — это поляризация, которая либо присуща полярным молекулам (ориентационная поляризация), либо может быть вызвана в любой молекуле, в которой возможно асимметричное искажение ядер (искаженная поляризация). Ориентационная поляризация возникает из-за постоянного диполя, например, который возникает из-за угла 104,45° между асимметричными связями между атомами кислорода и водорода в молекуле воды, что сохраняет поляризацию в отсутствие внешнего электрического поля. Сборка этих диполей образует макроскопическую поляризацию.
При приложении внешнего электрического поля расстояние между зарядами внутри каждого постоянного диполя, что связано с химической связью , остается постоянным в ориентационной поляризации; однако направление самой поляризации вращается. Это вращение происходит во временной шкале, которая зависит от крутящего момента и окружающей локальной вязкости молекул. Поскольку вращение не мгновенно, дипольные поляризации теряют реакцию на электрические поля на самых высоких частотах. Молекула вращается примерно на 1 радиан за пикосекунду в жидкости, таким образом, эта потеря происходит примерно на 10 11 Гц (в микроволновой области). Задержка реакции на изменение электрического поля вызывает трение и тепло.
Когда внешнее электрическое поле применяется на инфракрасных частотах или ниже, молекулы изгибаются и растягиваются полем, и молекулярный дипольный момент изменяется. Частота молекулярных колебаний примерно обратна времени, необходимому молекулам для изгиба, и эта искаженная поляризация исчезает выше инфракрасного диапазона.
Ионная поляризация
Ионная поляризация — это поляризация, вызванная относительными смещениями между положительными и отрицательными ионами в ионных кристаллах (например, NaCl ).
Если кристалл или молекула состоят из атомов более чем одного вида, распределение зарядов вокруг атома в кристалле или молекуле склоняется к положительному или отрицательному. В результате, когда колебания решетки или молекулярные колебания вызывают относительные смещения атомов, центры положительных и отрицательных зарядов также смещаются. Расположение этих центров зависит от симметрии смещений. Когда центры не соответствуют друг другу, в молекулах или кристаллах возникает поляризация. Такая поляризация называется ионной поляризацией .
Ионная поляризация вызывает сегнетоэлектрический эффект , а также дипольную поляризацию. Сегнетоэлектрический переход, который вызван выстраиванием ориентаций постоянных диполей вдоль определенного направления, называется фазовым переходом порядок-беспорядок . Переход, вызванный ионными поляризациями в кристаллах, называется фазовым переходом смещения .
В биологических клетках
Ионная поляризация обеспечивает выработку богатых энергией соединений в клетках ( протонный насос в митохондриях ), а также установление потенциала покоя на плазматической мембране , энергетически невыгодного транспорта ионов и межклеточной коммуникации ( Na+/K+-АТФаза ).
Все клетки в тканях тела животных электрически поляризованы – другими словами, они поддерживают разность потенциалов на плазматической мембране клетки , известную как мембранный потенциал . Эта электрическая поляризация является результатом сложного взаимодействия между ионными транспортерами и ионными каналами .
В нейронах типы ионных каналов в мембране обычно различаются в разных частях клетки, что придает дендритам , аксону и телу клетки разные электрические свойства. В результате некоторые части мембраны нейрона могут быть возбудимыми (способными генерировать потенциалы действия), а другие — нет.
Диэлектрическая дисперсия
В физике диэлектрическая дисперсия — это зависимость диэлектрической проницаемости диэлектрического материала от частоты приложенного электрического поля. Поскольку между изменениями поляризации и изменениями электрического поля существует задержка, диэлектрическая проницаемость диэлектрика является сложной функцией частоты электрического поля. Диэлектрическая дисперсия очень важна для применения диэлектрических материалов и анализа поляризационных систем.
Это один из примеров общего явления, известного как дисперсия материала : частотно-зависимая реакция среды на распространение волн.
Когда частота становится выше:
- Дипольная поляризация больше не может следовать колебаниям электрического поля в микроволновой области около 10 10 Гц ,
- Ионная поляризация и молекулярная поляризация искажения больше не могут отслеживать электрическое поле за пределами инфракрасной или дальней инфракрасной области около 10 13 Гц,
- Электронная поляризация теряет свою чувствительность в ультрафиолетовой области около 10 15 Гц.
В области частот выше ультрафиолета диэлектрическая проницаемость приближается к константе ε 0 в каждом веществе, где ε 0 — диэлектрическая проницаемость свободного пространства. Поскольку диэлектрическая проницаемость указывает на силу связи между электрическим полем и поляризацией, если процесс поляризации теряет свою реакцию, диэлектрическая проницаемость уменьшается.
Диэлектрическая релаксация
Диэлектрическая релаксация — это мгновенная задержка (или отставание) диэлектрической проницаемости материала. Обычно это вызвано задержкой молекулярной поляризации относительно изменяющегося электрического поля в диэлектрической среде (например, внутри конденсаторов или между двумя большими проводящими поверхностями). Диэлектрическую релаксацию в изменяющихся электрических полях можно считать аналогичной гистерезису в изменяющихся магнитных полях (например, в сердечниках катушек индуктивности или трансформаторов ). Релаксация в целом — это задержка или отставание в реакции линейной системы , и поэтому диэлектрическая релаксация измеряется относительно ожидаемых линейных стационарных (равновесных) значений диэлектрической проницаемости. Временная задержка между электрическим полем и поляризацией подразумевает необратимую деградацию свободной энергии Гиббса .
В физике диэлектрическая релаксация относится к релаксационному отклику диэлектрической среды на внешнее, осциллирующее электрическое поле. Эта релаксация часто описывается в терминах диэлектрической проницаемости как функции частоты , которая для идеальных систем может быть описана уравнением Дебая. С другой стороны, искажение, связанное с ионной и электронной поляризацией, демонстрирует поведение резонансного или осцилляторного типа . Характер процесса искажения зависит от структуры, состава и окружения образца.
релаксация Дебая
Релаксация Дебая — это реакция диэлектрической релаксации идеальной, невзаимодействующей популяции диполей на переменное внешнее электрическое поле. Обычно она выражается через комплексную диэлектрическую проницаемость ε среды как функцию угловой частоты поля ω :
где ε ∞ — диэлектрическая проницаемость на пределе высокой частоты, Δ ε = ε s − ε ∞, где ε s — статическая низкочастотная диэлектрическая проницаемость, а τ — характерное время релаксации среды. Разделение на действительную и мнимую части комплексной диэлектрической проницаемости дает: [10]
Обратите внимание, что приведенное выше уравнение для иногда записывается с в знаменателе из-за продолжающейся неоднозначности соглашения о знаках, в результате чего многие источники представляют временную зависимость комплексного электрического поля с помощью , тогда как другие используют . В первом соглашении функции и , представляющие действительную и мнимую части, задаются как , тогда как во втором соглашении . Приведенное выше уравнение использует последнее соглашение. [11]
Диэлектрические потери также представлены тангенсом угла потерь:
Эта модель релаксации была введена и названа в честь физика Питера Дебая (1913). [12] Она характерна для динамической поляризации с единственным временем релаксации.
Варианты уравнения Дебая
- Уравнение Коула–Коула
- Это уравнение используется, когда пик диэлектрических потерь показывает симметричное уширение.
- Уравнение Коула–Дэвидсона
- Это уравнение используется, когда пик диэлектрических потерь показывает асимметричное уширение.
- Релаксация Гавриляка–Негами
- Это уравнение учитывает как симметричное, так и асимметричное уширение.
- Функция Кольрауша–Вильямса–Уоттса
- Преобразование Фурье растянутой показательной функции .
- Закон Кюри-фон Швейдлера
- Это показывает, что реакция диэлектриков на приложенное постоянное поле ведет себя в соответствии со степенным законом, который можно выразить как интеграл над взвешенными экспоненциальными функциями.
- Приближение Джорджевича–Саркара
- Это используется, когда диэлектрические потери приблизительно постоянны для широкого диапазона частот.
Параэлектричество
Параэлектричество — это номинальное поведение диэлектриков, когда тензор диэлектрической проницаемости пропорционален единичной матрице, т. е. приложенное электрическое поле вызывает поляризацию и/или выравнивание диполей только параллельно приложенному электрическому полю. В отличие от аналогии с парамагнитным материалом, в параэлектрическом материале не должно быть постоянного электрического диполя . Удаление полей приводит к тому, что дипольная поляризация возвращается к нулю. [13] Механизмами, вызывающими параэлектрическое поведение, являются искажение отдельных ионов (смещение электронного облака из ядра) и поляризация молекул или комбинаций ионов или дефектов.
Параэлектричество может возникать в кристаллических фазах, где электрические диполи не выровнены и, таким образом, имеют потенциал выстраиваться во внешнем электрическом поле и ослаблять его.
Большинство диэлектрических материалов являются параэлектриками. Конкретным примером параэлектрического материала с высокой диэлектрической проницаемостью является титанат стронция .
Кристалл LiNbO 3 является сегнетоэлектриком ниже 1430 К , а выше этой температуры он переходит в неупорядоченную параэлектрическую фазу. Аналогично, другие перовскиты также проявляют параэлектричество при высоких температурах.
Параэлектричество было исследовано как возможный механизм охлаждения; поляризация параэлектрика путем приложения электрического поля в условиях адиабатического процесса повышает температуру, в то время как удаление поля понижает температуру. [14] Тепловой насос , который работает путем поляризации параэлектрика, позволяя ему вернуться к температуре окружающей среды (рассеивая излишнее тепло), приводя его в контакт с охлаждаемым объектом и, наконец, деполяризуя его, приведет к охлаждению.
Настраиваемость
Настраиваемые диэлектрики — это изоляторы, способность которых хранить электрический заряд изменяется при приложении напряжения. [15]
Обычно титанат стронция ( SrTiO
3) используется для устройств, работающих при низких температурах, а титанат бария-стронция ( Ba
1−xСр
хTiO
3) заменители для приборов комнатной температуры. Другие потенциальные материалы включают микроволновые диэлектрики и композиты из углеродных нанотрубок (CNT). [15] [16] [17]
В 2013 году многослойные слои титаната стронция, перемежающиеся с одинарными слоями оксида стронция, создали диэлектрик, способный работать на частоте до 125 ГГц. Материал был создан с помощью молекулярно-лучевой эпитаксии . У них несовпадающие кристаллические расстояния, что создает напряжение внутри слоя титаната стронция, что делает его менее стабильным и настраиваемым. [15]
Системы, такие как Ba
1−xСр
хTiO
3имеют параэлектрический-сегнетоэлектрический переход чуть ниже температуры окружающей среды, обеспечивая высокую настраиваемость. Пленки терпят значительные потери, возникающие из-за дефектов.
Приложения
Конденсаторы
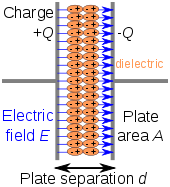
Конденсаторы промышленного производства обычно используют твердый диэлектрический материал с высокой диэлектрической проницаемостью в качестве промежуточной среды между сохраненными положительными и отрицательными зарядами. Этот материал часто упоминается в технических контекстах как диэлектрик конденсатора . [18]
Наиболее очевидным преимуществом использования такого диэлектрического материала является то, что он предотвращает прямой электрический контакт проводящих пластин, на которых хранятся заряды. Однако, что еще более важно, высокая диэлектрическая проницаемость позволяет хранить больший заряд при заданном напряжении. Это можно увидеть, рассмотрев случай линейного диэлектрика с диэлектрической проницаемостью ε и толщиной d между двумя проводящими пластинами с однородной плотностью заряда σ ε . В этом случае плотность заряда определяется как
и емкость на единицу площади на
Отсюда легко увидеть, что большее значение ε приводит к большему запасенному заряду и, следовательно, большей емкости.
Диэлектрические материалы, используемые для конденсаторов, также выбираются таким образом, чтобы они были устойчивы к ионизации . Это позволяет конденсатору работать при более высоких напряжениях, прежде чем изолирующий диэлектрик ионизуется и начинает пропускать нежелательный ток.
Диэлектрический резонатор
Диэлектрический резонаторный генератор (DRO) — это электронный компонент, который демонстрирует резонанс поляризационного отклика для узкого диапазона частот, как правило, в диапазоне СВЧ. Он состоит из «шайбы» из керамики, которая имеет большую диэлектрическую постоянную и низкий коэффициент рассеяния . Такие резонаторы часто используются для обеспечения опорной частоты в цепи генератора. Неэкранированный диэлектрический резонатор может использоваться в качестве диэлектрической резонаторной антенны (DRA).
Тонкие пленки BST
С 2002 по 2004 год Исследовательская лаборатория армии США (ARL) проводила исследования по технологии тонких пленок. Титанат бария-стронция (BST), тонкая сегнетоэлектрическая пленка, изучалась для изготовления радиочастотных и микроволновых компонентов, таких как управляемые напряжением генераторы, перестраиваемые фильтры и фазовращатели. [19]
Исследование было частью усилий по обеспечению армии высоконастраиваемыми, совместимыми с микроволнами материалами для широкополосных настраиваемых устройств с электрическим полем, которые стабильно работают при экстремальных температурах. [20] Эта работа улучшила настраиваемость объемного титаната бария-стронция, который является тонким пленочным средством для электронных компонентов. [21]
В исследовательской работе 2004 года исследователи из Американской лабораторией лазерной физики (ARL) изучили, как малые концентрации акцепторных легирующих примесей могут кардинально изменить свойства сегнетоэлектрических материалов, таких как BST. [22]
Исследователи «легировали» тонкие пленки BST магнием, анализируя «структуру, микроструктуру, морфологию поверхности и качество состава пленки/подложки» результата. Пленки BST, легированные Mg, показали «улучшенные диэлектрические свойства, низкий ток утечки и хорошую настраиваемость», что заслуживало потенциала для использования в микроволновых настраиваемых устройствах. [19]
Некоторые практические диэлектрики
Диэлектрические материалы могут быть твердыми, жидкими или газообразными. (Высокий вакуум также может быть полезным, [23] почти без потерь диэлектриком, даже если его относительная диэлектрическая проницаемость равна всего лишь единице.)
Твердые диэлектрики, пожалуй, наиболее часто используемые диэлектрики в электротехнике, и многие твердые тела являются очень хорошими изоляторами. Некоторые примеры включают фарфор , стекло и большинство пластиков . Воздух, азот и гексафторид серы являются тремя наиболее часто используемыми газообразными диэлектриками .
- Промышленные покрытия, такие как парилен, создают диэлектрический барьер между подложкой и окружающей средой.
- Минеральное масло широко используется внутри электрических трансформаторов в качестве жидкого диэлектрика и для охлаждения. Диэлектрические жидкости с более высокой диэлектрической проницаемостью, такие как электротехническое касторовое масло , часто используются в высоковольтных конденсаторах для предотвращения коронного разряда и увеличения емкости.
- Поскольку диэлектрики сопротивляются потоку электричества, поверхность диэлектрика может удерживать скрученные избыточные электрические заряды. Это может произойти случайно, когда диэлектрик трется ( трибоэлектрический эффект ). Это может быть полезно, как в генераторе Ван де Граафа или электрофоре , или может быть потенциально разрушительным, как в случае электростатического разряда .
- Специально обработанные диэлектрики, называемые электретами (которые не следует путать с сегнетоэлектриками ), могут сохранять избыточный внутренний заряд или «замороженную» поляризацию. Электреты имеют полупостоянное электрическое поле и являются электростатическим эквивалентом магнитов. Электреты имеют многочисленные практические применения в быту и промышленности.
- Некоторые диэлектрики могут генерировать разность потенциалов при воздействии механического напряжения или (что эквивалентно) изменять физическую форму, если к материалу приложено внешнее напряжение. Это свойство называется пьезоэлектричеством . Пьезоэлектрические материалы — еще один класс очень полезных диэлектриков.
- Некоторые ионные кристаллы и полимерные диэлектрики проявляют спонтанный дипольный момент, который может быть обращен внешним приложенным электрическим полем. Такое поведение называется сегнетоэлектрическим эффектом . Эти материалы аналогичны поведению ферромагнитных материалов в приложенном внешнем магнитном поле. Сегнетоэлектрические материалы часто имеют очень высокие диэлектрические постоянные, что делает их весьма полезными для конденсаторов.
Смотрите также
- Классификация материалов по диэлектрической проницаемости
- Парамагнетизм
- соотношение Клаузиуса-Моссотти
- Диэлектрическое поглощение
- Диэлектрические потери
- Диэлектрическая прочность
- Диэлектрическая спектроскопия
- Диэлектрик класса 1 EIA
- Диэлектрик класса 2 EIA
- Диэлектрик с высоким κ
- Диэлектрик с низким κ
- Утечка
- Линейная функция отклика
- Метаматериал
- задержка RC
- Вращательное броуновское движение
- Закон Пашена – изменение диэлектрической прочности газа в зависимости от давления
- Сепаратор (электричество)
Ссылки
- ^ ab "Dielectric". Encyclopædia Britannica . Chicago , Illinois : Encyclopædia Britannica, Inc. Архивировано из оригинала 27 апреля 2021 г. Получено 20 ноября 2021 г.
Диэлектрик, изоляционный материал или очень плохой проводник электрического тока. Когда диэлектрики помещаются в электрическое поле, в них практически не течет ток.
- ^ Артур Р. фон Хиппель в своей основополагающей работе «Диэлектрические материалы и их применение» утверждал: « Диэлектрики ... не являются узким классом так называемых изоляторов, а широким кругом неметаллов, рассматриваемых с точки зрения их взаимодействия с электрическими, магнитными или электромагнитными полями. Таким образом, мы имеем дело с газами, а также с жидкостями и твердыми телами, а также с хранением электрической и магнитной энергии, а также с ее рассеиванием». (стр. 1) (Technology Press of MIT and John Wiley, NY, 1954).
- ^ Томс, Э.; Сиппель, П.; и др. (2017). «Диэлектрическое исследование смесей ионных жидкостей». Sci. Rep . 7 (1): 7463. arXiv : 1703.05625 . Bibcode :2017NatSR...7.7463T. doi :10.1038/s41598-017-07982-3. PMC 5547043 . PMID 28785071.
- ^ Белкин, А.; Безрядин, А.; Хендрен, Л.; Хаблер, А. (2017). «Восстановление наноконденсаторов из оксида алюминия после пробоя при высоком и низком напряжении». Sci. Rep . 7 (1): 932. Bibcode :2017NatSR...7..932B. doi :10.1038/s41598-017-01007-9. PMC 5430567 . PMID 28428625.
- ^ Хоссейн, Шадиб (27.12.2020). «Характеристика злокачественных клеток с помощью математического анализа биоимпеданса и оптических свойств». Электромагнитная биология и медицина . 40 (1): 65–83. doi : 10.1080/15368378.2020.1850471. ISSN 1536-8378. PMID 33356700. S2CID 229694503.
- ^ Хоссейн, Шадиб (2020-04-02). «Биодиэлектрический феномен для активно дифференцирующихся злокачественных и нормальных клеток: обзор». Электромагнитная биология и медицина . 39 (2): 89–96. doi :10.1080/15368378.2020.1737804. ISSN 1536-8378. PMID 32138569. S2CID 212565141.
- ^ Дейнтит, Дж. (1994). Биографическая энциклопедия ученых . CRC Press. стр. 943. ISBN 978-0-7503-0287-6.
- ↑ Джеймс, Фрэнк А. Дж. Л., редактор. Переписка Майкла Фарадея, том 3, 1841–1848, «Письмо 1798, Уильям Уэвелл Фарадею, стр. 442». Архивировано из оригинала 2016-12-23 . Получено 2012-05-18 .Институт инженеров-электриков, Лондон, Соединенное Королевство, 1996. ISBN 0-86341-250-5
- ^ Микроволновая техника – RS Rao (проф.) . Получено 2013-11-08 .
- ^ Као, Кван Чи (2004). Диэлектрические явления в твердых телах . Лондон: Elsevier Academic Press. С. 92–93. ISBN 978-0-12-396561-5.
- ^ Бёттхер, К. Дж. Ф. (1952). Теория электрической поляризации . Лондон: Elsevier Publishing Companys. С. 231–232, 348–349.
- ↑ Debye, P. (1913), Ver. Deut. Phys. Gesell. 15, 777; перепечатано в 1954 году в сборнике статей Peter JW Debye. Interscience, Нью-Йорк
- ^ Chiang, Y. (1997). Физическая керамика . Нью-Йорк: John Wiley & Sons .
- ^ Kuhn, U.; Lüty, F. (1965). «Параэлектрическое нагревание и охлаждение с ОН-диполями в щелочных галогенидах». Solid State Communications . 3 (2): 31. Bibcode : 1965SSCom...3...31K. doi : 10.1016/0038-1098(65)90060-8.
- ^ abc Ли, Че-Хуэй; Орлофф, Натан Д.; Бироль, Туран; Чжу, Йе; Гоян, Вероника; Рокас, Эдуард; Хайслмайер, Райан; Влахос, Эфтихия; Манди, Джулия А.; Куркутис, Лена Ф.; Ни, Юэфэн; Биегальский, Майкл Д.; Чжан, Цзиншу; Бернхаген, Маргитта; Бенедек, Николь А.; Ким, Йонгсам; Брок, Джоэл Д.; Юккер, Рейнхард; Си, XX; Гопалан, Венкатраман; Нужный, Дмитрий; Камба, Станислав; Мюллер, Дэвид А.; Такеучи, Ичиро; Бут, Джеймс К.; Фенни, Крейг Дж.; Шлом, Даррелл Г. (2013). «Использование размерности и смягчение дефектов для создания настраиваемых микроволновых диэлектриков». Nature . 502 (7472): 532–536. Bibcode :2013Natur.502..532L. doi :10.1038/nature12582. hdl :2117/21213. PMID 24132232. S2CID 4457286.
- ^ Kong, LB; Li, S.; Zhang, TS; Zhai, JW; Boey, FYC; Ma, J. (2010-11-30). «Электрически настраиваемые диэлектрические материалы и стратегии улучшения их характеристик». Progress in Materials Science . 55 (8): 840–893. doi :10.1016/j.pmatsci.2010.04.004. hdl : 10356/93905 .
- ^ Giere, A.; Zheng, Y.; Maune, H.; Sazegar, M.; Paul, F.; Zhou, X.; Binder, JR; Muller, S.; Jakoby, R. (2008). "Tunable dielectrics for microwave applications". 2008 17th IEEE International Symposium on the Applications of Ferroelectrics . p. 1. doi :10.1109/ISAF.2008.4693753. ISBN 978-1-4244-2744-4. S2CID 15835472.
- ^ Мюссиг, Ганс-Иоахим. Полупроводниковый конденсатор с оксидом празеодима в качестве диэлектрика , патент США 7,113,388 , опубликованный 2003-11-06, выданный 2004-10-18, переданный IHP GmbH-Инновации для высокопроизводительной микроэлектроники/Институт инновационной микроэлектроники
- ^ ab Cole, MW; Geyer, RG (2004). "Новые тонкие пленки BST с настраиваемым акцептором для высококачественных настраиваемых микроволновых устройств". Revista Mexicana de Fisica . 50 (3): 232. Bibcode : 2004RMxF...50..232C.
- ^ Наир, К. М.; Го, Руян; Бхалла, Амар С.; Хирано, С.-И.; Суворов, Д. (2012-04-11). Разработки в области диэлектрических материалов и электронных устройств: Труды 106-го ежегодного собрания Американского керамического общества, Индианаполис, Индиана, США, 2004. John Wiley & Sons. ISBN 9781118408193.
- ^ Наир, К. М.; Бхалла, Амар С.; Хирано, С.-И.; Суворов, Д.; Шварц, Роберт В.; Чжу, Вэй (2012-04-11). Керамические материалы и многослойные электронные устройства. John Wiley & Sons. ISBN 9781118406762.
- ^ Cole, MW; Hubbard, C.; Ngo, E.; Ervin, M.; Wood, M.; Geyer, RG (июль 2002 г.). «Структурно-свойственные связи в чистых и легированных акцепторами тонких пленках Ba1−xSrxTiO3 для применения в перестраиваемых микроволновых устройствах». Journal of Applied Physics . 92 (1): 475–483. Bibcode :2002JAP....92..475C. doi :10.1063/1.1484231. ISSN 0021-8979.
- ^ Лион, Дэвид (2013). «Зависимость диэлектрической прочности в нановакуумных зазорах от размера зазора». Труды IEEE по диэлектрикам и электроизоляции . 20 (4): 1467–1471. doi :10.1109/TDEI.2013.6571470. S2CID 709782.
Дальнейшее чтение
- Джексон, Джон Дэвид (10 августа 1998 г.) [1962]. Классическая электродинамика (3-е изд.). John Wiley & Sons . ISBN 978-0-471-30932-1. OCLC 535998.
- Скейф, Брендан К. П. (3 сентября 1998 г.). Принципы диэлектриков. Монографии по физике и химии материалов (2-е изд.). Oxford University Press . ISBN 978-0-198-56557-4.
Внешние ссылки
- Лекция Фейнмана о диэлектриках
- Диэлектрическая сфера в электрическом поле
- Распространение ИТ для продвижения материаловедения (DoITPoMS) Учебно-методический пакет «Диэлектрические материалы» от Кембриджского университета
 Тексты на Викиресурсе:
Тексты на Викиресурсе:- «Диэлектрик». Энциклопедия Американа . 1920.
- «Диэлектрик». Энциклопедия Британника (11-е изд.). 1911.






















![{\displaystyle {\begin{align}\varepsilon '&=\varepsilon _{\infty }+{\frac {\varepsilon _{s}-\varepsilon _{\infty }}{1+\omega ^{2}\tau ^{2}}}\\[3pt]\varepsilon ''&={\frac {(\varepsilon _{s}-\varepsilon _{\infty })\omega \tau }{1+\omega ^{2}\tau ^{2}}}\end{align}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b380f6753bf58cda57ac2737341a9edcea387a72)









