Кельвин
| кельвин | |
|---|---|
 Эквивалентные температуры в градусах Кельвина (К), Цельсия (°C) и Фаренгейта (°F) | |
| Общая информация | |
| Система единиц | СИ |
| Единица измерения | температура |
| Символ | К |
| Назван в честь | Уильям Томсон, 1-й барон Кельвин |
| Определение 2019 года | к Б ≝1,380 649 × 10 −23 Дж./К |
| Конверсии | |
| х К в ... | ... соответствует ... |
| Производные единицы СИ | ( х − 273,15) °С |
| Имперские / американские единицы | (1,8 х − 459,67) °F |
| Абсолютная шкала Империи/США | 1,8 х °Ra |
Кельвин (символ: K ) — базовая единица измерения температуры в Международной системе единиц (СИ). Шкала Кельвина — это абсолютная температурная шкала , которая начинается с минимально возможной температуры ( абсолютного нуля ), принимаемой за 0 K. [1] [2] [3] [4] По определению, шкала Цельсия (символ °C) и шкала Кельвина имеют одинаковую величину; то есть повышение на 1 K равно повышению на 1 °C и наоборот, и любую температуру в градусах Цельсия можно преобразовать в кельвины, прибавив 273,15. [1] [5]
Шкалу первым разработал и предложил британский ученый XIX века лорд Кельвин . [5] В начале XX века ее часто называли «абсолютной шкалой Цельсия». [6] Кельвин был официально добавлен в Международную систему единиц в 1954 году, определив 273,16 К как тройную точку воды . Шкалы Цельсия, Фаренгейта и Ренкина были переопределены в терминах шкалы Кельвина с использованием этого определения. [2] [7] [8] В пересмотренной версии СИ 2019 года кельвин теперь определяется в терминах энергии, путем установки постоянной Больцмана в точности 1,380 649 × 10 −23 джоулей на кельвин; [2] каждое изменение термодинамической температуры на 1 К соответствует изменению тепловой энергии ровно на1,380 649 × 10−23 Дж .
История
Прекурсоры

В XVIII веке были разработаны многочисленные температурные шкалы , [9] в частности, шкала Фаренгейта и шкала Цельсия (позже шкала Цельсия). Эти шкалы предшествовали большей части современной науки термодинамики , включая атомную теорию и кинетическую теорию газов , которые лежат в основе концепции абсолютного нуля. Вместо этого они выбрали определяющие точки в пределах человеческого опыта, которые можно было легко и с разумной точностью воспроизвести, но которые не имели глубокого значения в теплофизике. В случае шкалы Цельсия (и давно не существующих шкалы Ньютона и шкалы Реомюра ) точка плавления льда служила такой отправной точкой, причем шкала Цельсия определялась (с 1740-х по 1940-е годы ) путем калибровки термометра таким образом, что:
- Температура замерзания воды составляет 0 °C.
- Температура кипения воды составляет 100 °C.
Это определение предполагает чистую воду при определенном давлении, выбранном для приближения к естественному давлению воздуха на уровне моря. Таким образом, приращение на 1 °C равно 1/100 разницы температур плавления и кипения. Этот же температурный интервал позднее использовался для шкалы Кельвина.
Закон Шарля
С 1787 по 1802 год Жак Шарль (неопубликовано), Джон Дальтон [10] [ 11] и Жозеф Луи Гей-Люссак [12] определили , что при постоянном давлении идеальные газы расширяются или сжимаются линейно ( закон Шарля ) примерно на 1/273 части на градус Цельсия при изменении температуры вверх или вниз в диапазоне от 0 °C до 100 °C. Экстраполяция этого закона показала, что газ, охлажденный примерно до -273 °C, будет занимать нулевой объем.
Лорд Кельвин

Первая абсолютная шкала
В 1848 году Уильям Томсон, который позже был пожалован титулом лорда Кельвина , опубликовал статью «Об абсолютной термометрической шкале» . [13] Шкала, предложенная в статье, оказалась неудовлетворительной, но принципы и формулы, на которых она была основана, были верны. [14] Например, в сноске Томсон вывел значение −273 °C для абсолютного нуля, вычислив отрицательную обратную величину 0,00366 — коэффициент теплового расширения идеального газа на градус Цельсия относительно точки замерзания льда. [15] Это выведенное значение согласуется с принятым в настоящее время значением −273,15 °C, что позволяет учесть точность и неопределенность, связанные с расчетом.
Шкала была разработана на том принципе, что «единица тепла, нисходящая от тела A при температуре T ° этой шкалы к телу B при температуре ( T − 1)° , даст тот же самый механический эффект, каково бы ни было число T ». [16] В частности, Томсон выразил количество работы, необходимое для производства единицы тепла ( тепловой КПД ), как , где — температура в градусах Цельсия, — коэффициент теплового расширения, а — «функция Карно», независимая от вещества величина, зависящая от температуры, [17] мотивированная устаревшей версией теоремы Карно . [14] [18] Шкала выводится путем нахождения изменения переменных температуры, такого, что пропорционально .

Когда Томсон опубликовал свою статью в 1848 году, он рассматривал только экспериментальные измерения Реньо . [19] В том же году Джеймс Прескотт Джоуль предположил Томсону, что истинная формула для функции Карно была [20] где - «механический эквивалент единицы тепла», [21] теперь называемая удельной теплоемкостью воды, приблизительно 771,8 футо-фунта силы на градус Фаренгейта на фунт (4153 Дж/К/кг). [22] Томсон изначально скептически отнесся к отклонениям формулы Джоуля от эксперимента, заявив: «Я думаю, что будет общепризнанно, что не может быть такой неточности в части данных Реньо, и остается только неопределенность относительно плотности насыщенного пара». [23] Томсон назвал правильность формулы Джоуля « гипотезой Майера », поскольку она была впервые принята Майером. [24] Томсон провел многочисленные эксперименты совместно с Джоулем, в конечном итоге придя к выводу к 1854 году, что формула Джоуля верна, а влияние температуры на плотность насыщенного пара объясняет все расхождения с данными Реньо. [25] Таким образом, в терминах современной шкалы Кельвина первую шкалу можно выразить следующим образом: [18] Параметры шкалы были произвольно выбраны так, чтобы совпадать со шкалой Цельсия при 0° и 100 °C или 273 и 373 K (точки плавления и кипения воды). [26] В этой шкале увеличение примерно на 222 градуса соответствует удвоению температуры Кельвина, независимо от начальной температуры, а «бесконечный холод» ( абсолютный ноль ) имеет численное значение отрицательной бесконечности . [27]
Современная абсолютная шкала
Томсон понял, что с предложенной Джоулем формулой для , соотношение между работой и теплом для идеального термодинамического двигателя было просто константой . [28] В 1854 году Томсон и Джоуль сформулировали вторую абсолютную шкалу, которая была более практичной и удобной, согласуясь с воздушными термометрами для большинства целей. [29] В частности, «численная мера температуры должна быть просто механическим эквивалентом тепловой единицы, деленной на функцию Карно». [30]
Чтобы объяснить это определение, рассмотрим обратимый двигатель цикла Карно , где — количество тепловой энергии, переданной в систему, — тепло, покидающее систему, — работа, выполненная системой ( ), — температура горячего резервуара в градусах Цельсия, — температура холодного резервуара в градусах Цельсия. Функция Карно определяется как , а абсолютная температура — как . Находим соотношение . Предположив , получаем общий принцип абсолютной термодинамической температурной шкалы для двигателя Карно, . Можно показать, что определение соответствует термометрической температуре законов идеального газа . [31]
Это определение само по себе недостаточно. Томсон указал, что шкала должна иметь два свойства: [32]
- Абсолютные значения двух температур относятся друг к другу пропорционально отношению принятого к отданному теплу в идеальном термодинамическом двигателе, работающем с источником и холодильником при более высокой и более низкой из температур соответственно.
- Разницу температур между точками замерзания и кипения воды при стандартном атмосферном давлении следует называть 100 градусами. (То же самое приращение, что и в шкале Цельсия). Лучшие оценки Томсона на тот момент были таковы, что температура замерзания воды составляла 273,7 К, а температура кипения воды — 373,7 К. [33]
Эти два свойства будут представлены во всех будущих версиях шкалы Кельвина, хотя она еще не была известна под этим названием. В первые десятилетия 20-го века шкалу Кельвина часто называли «абсолютной шкалой Цельсия », указывая градусы Цельсия, отсчитываемые от абсолютного нуля, а не от точки замерзания воды, и используя тот же символ для обычных градусов Цельсия, °C. [6]
Стандарт тройной точки

В 1873 году старший брат Уильяма Томсона Джеймс ввел термин «тройная точка» [34] для описания комбинации температуры и давления , при которой твердая, жидкая и газообразная фазы вещества способны сосуществовать в термодинамическом равновесии . В то время как любые две фазы могут сосуществовать в диапазоне комбинаций температуры и давления (например, на точку кипения воды можно довольно сильно повлиять, повысив или понизив давление), условие тройной точки для данного вещества может возникнуть только при одном давлении и только при одной температуре. К 1940-м годам экспериментально измеренная тройная точка воды составляла около 0,6% от стандартного атмосферного давления и очень близка к 0,01 °C согласно историческому определению Цельсия, которое тогда использовалось.
В 1948 году шкала Цельсия была перекалибрована путем присвоения температуре тройной точки воды значения 0,01 °C точно [35] и допуская, чтобы точка плавления при стандартном атмосферном давлении имела эмпирически определенное значение (а фактическая точка плавления при давлении окружающей среды имела колеблющееся значение) близкое к 0 °C. Это было оправдано на том основании, что тройная точка, как считалось, давала более точно воспроизводимую опорную температуру, чем точка плавления. [36] Тройную точку можно было измерить с точностью ±0,0001 °C, в то время как точка плавления — всего лишь с точностью ±0,001 °C. [35]
В 1954 году, когда экспериментально было установлено, что абсолютный ноль составляет около −273,15 °C согласно определению °C, которое использовалось в то время, Резолюция 3 10-й Генеральной конференции по мерам и весам (CGPM) ввела новую международно стандартизированную шкалу Кельвина, которая определила тройную точку как точно 273,15 + 0,01 = 273,16 градуса Кельвина. [37] [38]
В 1967/1968 годах Резолюцией 3 13-й ГКМВ была переименована единица приращения термодинамической температуры в «кельвин», символ К, заменив «градус Кельвина», символ °К. [39] [40] [41] 13-я ГКМВ также постановила в Резолюции 4, что «кельвин, единица термодинамической температуры, равен дроби 1/273.16 термодинамической температуры тройной точки воды." [4] [42] [43]
После переопределения метра в 1983 году единственными единицами СИ, не определенными относительно других единиц, остались кельвин, секунда и килограмм.
В 2005 году, отметив, что на тройную точку может влиять изотопное соотношение водорода и кислорода, составляющих образец воды, и что это «теперь один из основных источников наблюдаемой изменчивости между различными реализациями тройной точки воды», Международный комитет мер и весов (CIPM), комитет CGPM, подтвердил, что для целей определения температуры тройной точки воды определение кельвина будет относиться к воде, имеющей изотопный состав, указанный для Венского стандарта средней океанической воды . [4] [44] [45]
Переопределение 2019 года

В 2005 году CIPM начал программу по переопределению кельвина (вместе с другими базовыми единицами SI ) с использованием более экспериментально строгого метода. В частности, комитет предложил переопределить кельвин таким образом, чтобы постоянная Больцмана ( k B ) приняла точное значение1,380 6505 × 10−23 Дж/К . [46] Комитет надеялся, что программа будет завершена вовремя для ее принятия CGPM на заседании 2011 года, но на заседании 2011 года решение было отложено до заседания 2014 года, когда оно будет рассматриваться как часть более крупной программы . [47] Задача состояла в том, чтобы избежать ухудшения точности измерений вблизи тройной точки. Переопределение было еще раз отложено в 2014 году в ожидании более точных измерений постоянной Больцмана в терминах текущего определения, [48] но было окончательно принято на 26-м CGPM в конце 2018 года со значением k B = 1,380 649 × 10 -23 Дж⋅К -1 . [49] [46] [1] [2] [4] [50]
Для научных целей главное преимущество переопределения заключается в возможности более точных измерений при очень низких и очень высоких температурах, поскольку используемые методы зависят от постоянной Больцмана. Независимость от какого-либо конкретного вещества или измерения также является философским преимуществом. Теперь кельвин зависит только от постоянной Больцмана и универсальных констант (см. диаграмму зависимостей единиц СИ 2019 года), что позволяет выразить кельвин точно так же: [2]
- 1 кельвин = 1,380 649 × 10 −23/(6,626 070 15 × 10 −34 )(9 192 631 770 ) h Δ ν Cs/к Б = 13.806 49/6.091 102 297 113 866 55 h Δ ν Cs/к Б .
Для практических целей переопределение осталось незамеченным; для постоянной Больцмана было использовано достаточно цифр, чтобы гарантировать, что 273,16 К имеет достаточно значимых цифр , чтобы содержать неопределенность тройной точки воды [51] , и вода все еще обычно замерзает при 0 °C [52] с высокой степенью точности. Но до переопределения тройная точка воды была точной, а постоянная Больцмана имела измеренное значение1,380 649 03 (51) × 10 −23 Дж/К , с относительной стандартной неопределенностью3,7 × 10−7 . [51] После этого постоянная Больцмана становится точной, а неопределенность переносится на тройную точку воды, которая теперь273.1600(1) К . [а]
Новое определение официально вступило в силу 20 мая 2019 года, в 144-ю годовщину Метрической конвенции . [50] [1] [2] [4]
Практическое использование
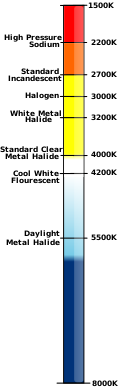
Цветовая температура
Кельвин часто используется как мера цветовой температуры источников света. Цветовая температура основана на принципе, что излучатель черного тела излучает свет с распределением частот, характерным для его температуры. Черные тела при температурах ниже примерно4000 К кажутся красноватыми, тогда как выше примерно7500 К кажутся голубоватыми. Цветовая температура важна в области проекции изображений и фотографии, где цветовая температура приблизительноДля соответствия эмульсиям плёнок «дневного света» требуется температура 5600 К.
В астрономии звездная классификация звезд и их место на диаграмме Герцшпрунга-Рассела основаны, в частности, на их поверхностной температуре, известной как эффективная температура . Фотосфера Солнца , например, имеет эффективную температуру5772 K [1][2][3][4], принятый резолюцией B3 МАС 2015 г.
Цифровые камеры и программное обеспечение для фотографирования часто используют цветовую температуру в K в меню редактирования и настройки. Простое руководство заключается в том, что более высокая цветовая температура создает изображение с улучшенными белыми и синими оттенками. Уменьшение цветовой температуры создает изображение, в котором больше преобладают красноватые, «теплые» цвета .
Кельвин как единица измерения температуры шума
В электронике кельвин используется как индикатор того, насколько шумна схема по отношению к предельному уровню шума , т. е. шумовой температуре . Шум Джонсона-Найквиста резисторов (который производит связанный шум kTC при сочетании с конденсаторами ) является типом теплового шума, полученного из постоянной Больцмана , и может использоваться для определения шумовой температуры схемы с использованием формул Фрииса для шума .
Производные единицы и кратные СИ
Единственная производная единица СИ со специальным названием, полученным от кельвина, — это градус Цельсия. Как и другие единицы СИ, кельвин также может быть изменен путем добавления метрической приставки , которая умножает его на степень 10 :
| Дробные числа | Множественные | ||||
|---|---|---|---|---|---|
| Ценить | символ СИ | Имя | Ценить | символ СИ | Имя |
| 10 −1 К | дК | децикельвин | 10 1 К | даК | декакельвин |
| 10 −2 К | сК | сантикельвин | 10 2 К | hK | гектокельвин |
| 10 −3 К | мК | милликельвин | 10 3 К | кК | килокельвин |
| 10 −6 К | мкК | микрокельвин | 10 6 К | МК | мегакельвин |
| 10 −9 К | нк | нанокельвин | 10 9 К | ГК | гигакельвин |
| 10 −12 К | пК | пикокельвин | 10 12 К | ТК | теракельвин |
| 10 −15 К | фК | фемтокельвин | 10 15 К | ПК | петакелвин |
| 10 −18 К | аК | аттокельвин | 10 18 К | ЭК | ексакельвин |
| 10 −21 К | zK | зептокельвин | 10 21 К | ЗК | зеттакельвин |
| 10 −24 К | yK | йоктокельвин | 10 24 К | ЮК | йоттакелвин |
| 10 −27 К | РК | ронтокельвин | 10 27 К | РК | роннакельвин |
| 10 −30 К | qK | квектокельвин | 10 30 К | КК | кеттакелвин |
Орфография
Согласно правилам СИ, кельвин никогда не упоминается и не пишется как градус . Слово «кельвин» не пишется с заглавной буквы, когда используется как единица. Оно может быть во множественном числе, если это уместно (например, «сейчас 283 кельвина снаружи», как и для «сейчас 50 градусов по Фаренгейту» и «10 градусов по Цельсию»). [54] [5] [55] [56] Символ единицы измерения K — заглавная буква, [39] согласно правилам СИ писать заглавные символы единиц, полученных от имени человека. [57] Принято писать Кельвин с заглавной буквы, когда речь идет о лорде Кельвине [5] или шкале Кельвина. [58]
Символ единицы измерения K кодируется в Unicode в кодовой точке U+212A K ЗНАК КЕЛЬВИНА . Однако это символ совместимости, предусмотренный для совместимости с устаревшими кодировками. Стандарт Unicode рекомендует использовать вместо него U+004B K ЛАТИНСКАЯ ЗАГЛАВНАЯ БУКВА K ; то есть обычную заглавную букву K . "Трем буквоподобным символам была дана каноническая эквивалентность обычным буквам: U+2126 Ω ЗНАК ОМ , U+212A K ЗНАК КЕЛЬВИНА и U+212B Å ЗНАК АНГСТРОМА . Во всех трех случаях следует использовать обычную букву." [59]
Смотрите также
- Сравнение температурных шкал
- Международная температурная шкала 1990 г.
- kT (энергия) – произведение постоянной Больцмана на температуру
- Отрицательная температура
- Очерк метрологии и измерений
Примечания
- ^ Абсолютную неопределенность можно рассчитать как 273,16 ×3,7 × 10−7 К , что можно округлить до0,10 мК для всех практических целей. [53]
Ссылки
- ^ abcd BIPM (2019-05-20). "Mise en pratique для определения кельвина в СИ". BIPM.org . Получено 2022-02-18 .
- ^ abcdef "Брошюра SI: Международная система единиц (SI) – 9-е издание (обновлено в 2022 г.)". BIPM . Получено 2022-09-07 .
- ^ "Базовая единица СИ: кельвин (К)". BIPM . Получено 2022-03-05 .
- ^ abcde «Поворотный момент для человечества: переосмысление мировой системы измерений». NIST . 2018-05-12 . Получено 2022-02-21 .
- ^ abcd "Кельвин: Введение". NIST . 2018-05-14 . Получено 2022-09-02 .
- ^ ab Издания энциклопедии «Британника» 1920-х и 1950-х годов, статья «Планеты».
- ^ Бенхэм, Элизабет (2020-10-06). «Разрушение мифов о метрической системе». NIST . Taking Measure (официальный блог NIST) . Получено 2022-02-21 .
- ^ "Справочник 44 – 2022 – Приложение C – Общие таблицы единиц измерения" (PDF) . nist.gov . NIST . Получено 21.02.2022 .
- ^ "Кельвин: История". NIST . 2018-05-14 . Получено 2022-02-21 .
- ^ Далтон, Джон (1801). «Очерк II. О силе пара или испарения из воды и различных других жидкостей, как в вакууме, так и в воздухе». Мемуары литературного и философского общества Манчестера . 5 часть 2: 550–574.
- ^ Далтон, Джон (1801). «Очерк IV. О расширении упругих жидкостей под действием тепла». Мемуары литературного и философского общества Манчестера . 5 часть 2: 595–602.
- ^ Гей-Люссак, Жозеф Луи (1802), «Recherches sur la dilatation des gaz et des vapeurs», Annales de Chimie , XLIII : 137. Перевод на английский язык (отрывок).
- ↑ Томсон 1882, стр. 100–106.
- ^ ab Magie, William Francis (1935). Справочник по физике. стр. 237.
- ↑ Томсон 1882, стр. 104: «Если мы достаточно далеко продвинем строгий принцип градуировки, изложенный выше, то мы должны прийти к точке, соответствующей уменьшению объема воздуха до нуля, что будет отмечено как -273° шкалы (-100/·366, если ·366 — коэффициент расширения); и, следовательно, -273° воздушного термометра — это точка, которая не может быть достигнута ни при какой конечной температуре, какой бы низкой она ни была».
- ↑ Томсон 1882, стр. 104.
- ↑ Томсон 1882, стр. 187.
- ^ Томсон 1882, стр. 106.
- ↑ Томсон 1882, стр. 193.
- ↑ Томсон 1882, стр. 212.
- ↑ Томсон 1882, стр. 186.
- ↑ Томсон 1882, стр. 192.
- ↑ Томсон 1882, стр. 214–215.
- ↑ Томсон 1882, стр. 213.
- ↑ Томсон 1882, стр. 388.
- ↑ Томсон 1882, стр. 105: «Произвольные точки, совпадающие на двух шкалах, — это 0° и 100°»
- ^ Saslow, WM (2020-01-07). "История термодинамики: недостающее руководство". Энтропия . 22 (1). уравнение (36). Bibcode : 2020Entrp..22...77S. doi : 10.3390 /e22010077 . PMC 7516509. PMID 33285852.
- ^ Томсон 1882, стр. 190, формула (7).
- ↑ Томсон 1882, стр. 106, 232–236.
- ↑ Томсон 1882, стр. 234.
- ^ Ван, Линь-Шу (2020). Трактат о тепле и энергии . Cham: Springer. стр. 77. ISBN 9783030057466.
- ↑ Томсон 1882, стр. 235.
- ↑ Томсон 1882, стр. 236.
- ^ Томсон, Джеймс (1873). «Количественное исследование некоторых отношений между газообразным, жидким и твердым состояниями водной субстанции». Труды Лондонского королевского общества . 22 : 28. Bibcode : 1873RSPS...22...27T. ISSN 0370-1662.
и, следовательно, что три кривые встретятся или пересекутся в одной точке, которую я назвал
тройной точкой
.
- ^ ab Swinton, FL (сентябрь 1967). "Триплетная точка воды". Journal of Chemical Education . 44 (9): 541. Bibcode : 1967JChEd..44..541S. doi : 10.1021/ed044p541. ISSN 0021-9584.
- ^ "Резолюция 3 9-й ГКМВ (1948)". BIPM . Получено 21.02.2022 .
- ^ "Резолюция 3 10-й ГКМВ (1954)". BIPM . Получено 21.02.2022 .
- ^ "Резолюция 3: Определение термодинамической шкалы температур". Резолюции 10-й ГКМВ . Международное бюро мер и весов. 1954. Архивировано из оригинала 2007-06-23 . Получено 2008-02-06 .
- ^ ab "Резолюция 3 13-й ГКМВ (1967)". BIPM . Получено 2022-02-21 .
- ^ "Резолюция 3: Единица термодинамической температуры СИ (кельвин)". Резолюции 13-й ГКМВ . Международное бюро мер и весов. 1967. Архивировано из оригинала 21-04-2007 . Получено 06-02-2008 .
- ^ Вестфаль, Вильгельм Генрих (1952). «Нокс, Дункеллеухтдихте, Скот». В Вестфале, Вильгельм Х. (ред.). Physikalisches Wörterbuch (на немецком языке) (1-е изд.). Берлин / Геттинген / Гейдельберг, Германия: Springer-Verlag OHG . стр. 125, 271, 389. doi :10.1007/978-3-662-12706-3. ISBN 978-3-662-12707-0. Проверено 16 марта 2023 г. стр. 271, 389:
Dunkelleuchtdichte. […] Unter Zugrundelegung dieser Empfindlichkeitskurve шляпный человек 1940 года в Германии die Dunkelleuchtdichte mit der Einheit Skot (sk) so festgesetzt, daß bei einem Licht der Farbtemperatur 2360 ° K 1 sk = 10 −3 asb позолота. 1948 год – это Международная Белеухтунгская Комиссия (IBK) с безграничной температурой при 2046 °K, с температурой платины , festgesetzt worden. Die Bezeichnung Skot wurde von der IBK nicht übernommen, dafür soll "skotopisches Stilb" gesagt werden. Als höchstzulässiger Grenzwert für die Dunkelleuchtdichte ist in Deutschland 10 Skot festgesetzt worden, um eine Verwendung der Dunkelleuchtdichte im Gebiet des gemischten Zapfen - und Stäbchensehens zu vermeiden, da in diesem Bereich die photometrischen Maßgrößen wegen der allmählich gleitenden Augenempfindlichkeitskurve ihren Sinn verlieren. [...] Скот, abgek[ürzt] sk, Einheit für die Dunkelleuchtdichte, welche für zahlenmäßige Angaben und zum Anschluß der Dunkelleuchtdichte an dienormale Leuchtdichte 1940 von der Deutschen Lichttechnischen Gesellschaft geschaffen wurde. Für diesen Anschluß wurde die Strahlung des schwarzen Körpers при T = 2360 °K, dh eine Strahlung der Farbtemperatur T 1 = 2360 °K vereinbart. Eine Lichtquelle strahlt mit der Dunkelleuchtdichte 1 sk, wenn sie photometrisch gleich einer Strahlung der Farbtemperatur T 2 = 2360 °K und der Leuchtdichte von 10 −3 asb (Apostilb) ist. Bei der Farbtemperatur T 1 = 2360 °K позолота также умирает. Соотношение: 1 sk = 10 −3 asb = 10 −7 /π sb.
- ^ "Резолюция 4 13-й ГКМВ (1967)". BIPM . Получено 21.02.2022 .
- ^ "Резолюция 4: Определение единицы термодинамической температуры (кельвин) в системе СИ". Резолюции 13-й ГКМВ . Международное бюро мер и весов. 1967. Архивировано из оригинала 15-06-2007 . Получено 06-02-2008 .
- ^ "Резолюция 10 23-й ГКМВ (2007)". BIPM . Получено 2022-02-21 .
- ^ "Единица термодинамической температуры (кельвин)". Брошюра SI, 8-е издание . Международное бюро мер и весов. 1967. Раздел 2.1.1.5. Архивировано из оригинала 2007-09-26 . Получено 2008-02-06 .
- ^ ab Ian Mills (29.09.2010). "Черновик главы 2 для брошюры SI, после переопределения основных единиц" (PDF) . BIPM . CCU. Архивировано из оригинала (PDF) 10.01.2011 . Получено 01.01.2011 .
- ^ "Генеральная конференция по мерам и весам утверждает возможные изменения в Международной системе единиц, включая переопределение килограмма" (PDF) (пресс-релиз). Севр, Франция: Генеральная конференция по мерам и весам . 2011-10-23. Архивировано из оригинала (PDF) 2012-02-09 . Получено 2011-10-25 .
- ^ Wood, B. (3–4 ноября 2014 г.). «Отчет о заседании целевой группы CODATA по фундаментальным константам» (PDF) . BIPM . стр. 7. Архивировано из оригинала (PDF) 2015-10-13.
[Директор BIPM Мартин] Милтон ответил на вопрос о том, что произойдет, если ... CIPM или CGPM проголосуют не продвигать вперед переопределение SI. Он ответил, что, по его мнению, к тому времени решение двигаться вперед следует рассматривать как предрешенный результат.
- ^ "2022 CODATA Value: Boltzmann constant". Справочник NIST по константам, единицам и неопределенности . NIST . Май 2024. Получено 2024-05-18 .
- ^ ab "Резолюция 1 26-й ГКМВ (2018)". BIPM . Получено 2022-02-21 .
- ^ ab Newell, DB; Cabiati, F; Fischer, J; Fujii, K; Karshenboim, SG; Margolis, HS; de Mirandés, E; Mohr, PJ; Nez, F; Pachucki, K; Quinn, TJ; Taylor, BN; Wang, M; Wood, BM; Zhang, Z; et al. (Целевая группа по фундаментальным константам Комитета по данным для науки и технологий (CODATA)) (29.01.2018). "Значения CODATA 2017 h, e, k и NA для пересмотра SI". Metrologia . 55 (1): L13–L16. Bibcode : 2018Metro..55L..13N . doi : 10.1088/1681-7575/aa950a .
- ^ "Обновление определения кельвина" (PDF) . BIPM . Архивировано из оригинала (PDF) 2008-11-23 . Получено 2010-02-23 .
- ^ Фишер, Дж; Феллмут, Б; Гайзер, С; Зандт, Т; Питре, Л; Спараски, Ф; Плиммер, доктор медицины; де Подеста, М; Андервуд, Р.; Саттон, Дж; Мачин, Г; Гавиозо, РМ; Мадонна Рипа, D; Стер, PPM; Цюй, Дж; Фэн, XJ; Чжан, Дж; Молдовер, MR; Бенц, СП; Уайт, ДР; Джанфрани, Л; Кастрильо, А; Моретти, Л; Дарке, Б; Муфаредж, Э; Даусси, К; Бриодо, С; Козлова О; Рисегари, Л; Сеговия, Джей-Джей; Мартин, MC; дель Кампо, защитник (01 апреля 2018 г.). «Проект Больцмана». Метрология . 55 (2): Р1–Р20. Bibcode : 2018Metro..55R...1F. doi : 10.1088/1681-7575/aaa790. PMC 6508687. PMID 31080297 .
- ^ "NIST Guide to the SI | Глава 9: Правила и соглашения по стилю написания названий единиц", NIST SP 811 , 2016-01-28,
Производная единица обычно имеет единственное число в английском языке, например, значение 3 м2
·
К/Вт обычно записывается как "три квадратных метра кельвина на ватт", а значение 3 Кл·м2
/
В обычно записывается как "три кулона на квадратный метр на вольт". Однако "единичная" единица может иметь множественное число; например, значение 5 кПа записывается как "пять килопаскалей", хотя "пять килопаскалей" приемлемо. Если в таком случае с одной единицей число меньше единицы, единица всегда имеет единственное число при написании; например, 0,5 кПа записывается как "пять десятых килопаскаля".
- ^ "Определение КЕЛЬВИНА". www.merriam-webster.com . Получено 21.08.2023 .
- ^ Руководство по стилю английского языка ЦЕРН (PDF) . ЦЕРН . 2022. стр. 64.
- ^ "Письмо с единицами СИ (метрической системы)". NIST . 2010-01-13.
- ^ Брэди, Джеймс Э.; Сенезе, Фред (2008-01-28). Химия, Учебное пособие для студентов: Изучение материи и ее изменений. John Wiley & Sons. стр. 15. ISBN 978-0-470-18464-6.
- ^ "22.2". Стандарт Unicode, версия 8.0 (PDF) . Маунтин-Вью, Калифорния, США: Консорциум Unicode. Август 2015 г. ISBN 978-1-936213-10-8. Архивировано (PDF) из оригинала 2016-12-06 . Получено 2015-09-06 .
Библиография
- Международное бюро мер и весов (2019). "Брошюра Международной системы единиц (СИ)" (PDF) . 9-е издание. Международный комитет мер и весов . Получено 28.04.2022 .
- Томсон, Уильям (лорд Кельвин) (1882). Математические и физические работы: Том I. Издательство Кембриджского университета.
Внешние ссылки
- Томсон, Уильям (октябрь 1848 г.). «Об абсолютной термометрической шкале, основанной на теории Карно о движущей силе тепла и вычисленной по наблюдениям Реньо». zapatopi.net . Философский журнал. Архивировано из оригинала 2008-02-01 . Получено 2022-02-21 .
- Томсон, Уильям (март 1851 г.). «О динамической теории тепла с численными результатами, выведенными из эквивалента тепловой единицы г-на Джоуля и наблюдений г-на Реньо над паром». zapatopi.net . Труды Королевского общества Эдинбурга . Получено 2024-05-05 .























