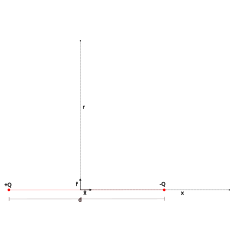
Электрическое поле
| Электрическое поле | |
|---|---|
Общие символы | Э |
| единица СИ | вольт на метр (В/м) |
| В основных единицах СИ | кг⋅м⋅с −3 ⋅А −1 |
| Измерение | М Л Т −3 Я −1 |
| Статьи о |
| Электромагнетизм |
|---|
 |
Электрическое поле (иногда называемое E-полем [1] ) — это физическое поле , которое окружает электрически заряженные частицы . Заряженные частицы оказывают друг на друга силы притяжения, когда их заряды противоположны, и отталкивают друг друга, когда их заряды одинаковы. Поскольку эти силы оказываются взаимно, для возникновения сил должны присутствовать два заряда. Электрическое поле одного заряда (или группы зарядов) описывает их способность оказывать такие силы на другой заряженный объект. Эти силы описываются законом Кулона , который гласит, что чем больше величина зарядов, тем больше сила, и чем больше расстояние между ними, тем слабее сила. Таким образом, мы можем неформально сказать, что чем больше заряд объекта, тем сильнее его электрическое поле. Аналогично, электрическое поле сильнее вблизи заряженных объектов и слабее вдали. Электрические поля возникают из электрических зарядов и изменяющихся во времени электрических токов . Электрические поля и магнитные поля являются проявлениями электромагнитного поля . Электромагнетизм — одно из четырех фундаментальных взаимодействий природы.
Электрические поля важны во многих областях физики и используются в электротехнике. Например, в атомной физике и химии взаимодействие в электрическом поле между атомным ядром и электронами является силой, которая удерживает эти частицы вместе в атомах. Аналогично, взаимодействие в электрическом поле между атомами является силой, ответственной за химическую связь , которая приводит к образованию молекул .
Электрическое поле определяется как векторное поле , которое сопоставляет каждой точке пространства силу на единицу заряда , действующую на бесконечно малый пробный заряд, покоящийся в этой точке. [2] [3] [4] Единицей СИ для электрического поля является вольт на метр (В/м), который равен ньютону на кулон ( Н/Кл). [5]
Описание

Электрическое поле определяется в каждой точке пространства как сила, которая будет испытываться бесконечно малым неподвижным пробным зарядом в этой точке, деленная на заряд. [6] : 469–70 Электрическое поле определяется в терминах силы , а сила является вектором ( т. е. имеет как величину , так и направление ), поэтому следует, что электрическое поле может быть описано векторным полем . [6] : 469–70 Электрическое поле действует между двумя зарядами аналогично тому, как гравитационное поле действует между двумя массами , поскольку они оба подчиняются закону обратных квадратов с расстоянием. [7] Это основа закона Кулона , который гласит, что для неподвижных зарядов электрическое поле изменяется в зависимости от заряда источника и изменяется обратно пропорционально квадрату расстояния от источника. Это означает, что если заряд источника удвоится, электрическое поле удвоится, а если вы отойдете вдвое дальше от источника, поле в этой точке будет составлять всего одну четверть от своей первоначальной силы.
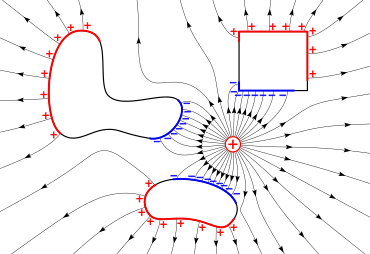
Электрическое поле можно визуализировать с помощью набора линий , направление которых в каждой точке совпадает с направлением поля, концепция, введенная Майклом Фарадеем [8] , чей термин « силовые линии » до сих пор иногда используется. Эта иллюстрация имеет полезное свойство, что, если нарисовать ее так, чтобы каждая линия представляла одинаковое количество потока , сила поля пропорциональна плотности линий. [9] Линии поля, обусловленные неподвижными зарядами, обладают несколькими важными свойствами, включая то, что они всегда берут начало от положительных зарядов и заканчиваются на отрицательных зарядах, они входят во все хорошие проводники под прямым углом и никогда не пересекаются и не замыкаются сами на себя. [6] : 479 Линии поля являются репрезентативной концепцией; поле фактически пронизывает все промежуточное пространство между линиями. Больше или меньше линий можно нарисовать в зависимости от точности, с которой требуется изобразить поле. [8] Изучение электрических полей, создаваемых неподвижными зарядами, называется электростатикой .
Закон Фарадея описывает связь между изменяющимся во времени магнитным полем и электрическим полем. Один из способов сформулировать закон Фарадея заключается в том, что ротор электрического поля равен отрицательной производной по времени магнитного поля. [10] : 327 При отсутствии изменяющегося во времени магнитного поля электрическое поле поэтому называется консервативным (т.е. безроторным). [10] : 24, 90–91 Это подразумевает, что существует два вида электрических полей: электростатические поля и поля, возникающие из изменяющихся во времени магнитных полей. [10] : 305–307 В то время как безроторная природа статического электрического поля допускает более простую трактовку с использованием электростатики, изменяющиеся во времени магнитные поля обычно рассматриваются как компонент единого электромагнитного поля . Изучение магнитных и электрических полей, которые изменяются со временем, называется электродинамикой .
Математическая формулировка
Электрические поля вызваны электрическими зарядами , описываемыми законом Гаусса , [11] и изменяющимися во времени магнитными полями , описываемыми законом индукции Фарадея . [12] Вместе эти законы достаточны для определения поведения электрического поля. Однако, поскольку магнитное поле описывается как функция электрического поля, уравнения обоих полей связаны и вместе образуют уравнения Максвелла , которые описывают оба поля как функцию зарядов и токов .

Электростатика
В частном случае устойчивого состояния (стационарные заряды и токи) индуктивный эффект Максвелла-Фарадея исчезает. Полученные два уравнения (закон Гаусса и закон Фарадея без индукционного члена ), взятые вместе, эквивалентны закону Кулона , который гласит, что частица с электрическим зарядом в положении оказывает силу на частицу с зарядом в положении : [13] где
- это сила, действующая на заряженную частицу со стороны заряженной частицы .
- ε 0 — диэлектрическая проницаемость свободного пространства .
- — единичный вектор, направленный от к .
- — вектор смещения от до .
Обратите внимание, что необходимо заменить на , диэлектрическую проницаемость , когда заряды находятся в непустых средах. Когда заряды и имеют одинаковый знак, эта сила положительна, направлена от другого заряда, указывая на то, что частицы отталкиваются друг от друга. Когда заряды имеют разные знаки, сила отрицательна, указывая на то, что частицы притягиваются. Чтобы упростить расчет силы Кулона на любой заряд в позиции это выражение можно разделить, оставив выражение, которое зависит только от другого заряда ( заряда источника ) [14] [4] где
- - составляющая электрического поля в точке, обусловленная .
Это электрическое поле в точке, вызванное точечным зарядом ; это векторная функция, равная силе Кулона на единицу заряда, которую положительный точечный заряд будет испытывать в положении . Поскольку эта формула дает величину и направление электрического поля в любой точке пространства (за исключением местоположения самого заряда, , где оно становится бесконечным), она определяет векторное поле . Из приведенной выше формулы видно, что электрическое поле, вызванное точечным зарядом, везде направлено от заряда, если он положительный, и к заряду, если он отрицательный, и его величина уменьшается обратно пропорционально квадрату расстояния от заряда.
Сила Кулона, действующая на заряд величиной в любой точке пространства, равна произведению заряда на напряжённость электрического поля в этой точке. Единицей измерения электрического поля в системе СИ является ньютон на кулон (Н/Кл) или вольт на метр (В/м); в основных единицах системы СИ это кг⋅м⋅с −3 ⋅А −1 .
Принцип суперпозиции
Вследствие линейности уравнений Максвелла электрические поля удовлетворяют принципу суперпозиции , который гласит, что полное электрическое поле в точке, обусловленное совокупностью зарядов, равно векторной сумме электрических полей в этой точке, обусловленных отдельными зарядами. [4] Этот принцип полезен при вычислении поля, созданного несколькими точечными зарядами. Если заряды неподвижны в пространстве в точках , при отсутствии токов принцип суперпозиции гласит, что результирующее поле является суммой полей, созданных каждой частицей, как описано законом Кулона: где
- единичный вектор в направлении от точки к точке
- — вектор смещения от точки к точке .
Непрерывное распределение заряда
Принцип суперпозиции позволяет рассчитать электрическое поле, обусловленное распределением плотности заряда . Рассматривая заряд в каждом малом объеме пространства в точке как точечный заряд, результирующее электрическое поле, , в точке можно рассчитать как где
- — единичный вектор, направленный из в .
- — вектор смещения от до .
Полное поле находится путем суммирования вкладов всех приращений объема путем интегрирования плотности заряда по объему :
Аналогичные уравнения следуют для поверхностного заряда с поверхностной плотностью заряда на поверхности и для линейных зарядов с линейной плотностью заряда на линии.
Электрический потенциал
Если система статична, то есть магнитные поля не изменяются во времени, то по закону Фарадея электрическое поле не имеет вихрей . В этом случае можно определить электрический потенциал , то есть функцию, такую что . [15] Это аналогично гравитационному потенциалу . Разность между электрическим потенциалом в двух точках пространства называется разностью потенциалов (или напряжением) между двумя точками.
Однако в общем случае электрическое поле не может быть описано независимо от магнитного поля. Учитывая магнитный векторный потенциал , A , определенный так, что , можно все еще определить электрический потенциал таким образом, что: где — градиент электрического потенциала, а — частная производная A по времени.
Закон индукции Фарадея можно восстановить , взяв ротор этого уравнения [16], которое апостериори оправдывает предыдущую форму для E.
Непрерывное и дискретное представление заряда
Уравнения электромагнетизма лучше всего описываются в непрерывном описании. Однако заряды иногда лучше всего описывать как дискретные точки; например, некоторые модели могут описывать электроны как точечные источники, где плотность заряда бесконечна на бесконечно малом участке пространства.
Заряд, расположенный в , можно математически описать как плотность заряда , где используется дельта-функция Дирака (в трех измерениях). Наоборот, распределение заряда можно аппроксимировать множеством малых точечных зарядов.
Электростатические поля

Электростатические поля — это электрические поля, которые не меняются со временем. Такие поля присутствуют, когда системы заряженной материи неподвижны или когда электрические токи не меняются. В этом случае закон Кулона полностью описывает поле. [17]
Параллели между электростатическими и гравитационными полями
Закон Кулона, описывающий взаимодействие электрических зарядов: аналогичен закону всемирного тяготения Ньютона : (где ).
Это предполагает сходство между электрическим полем E и гравитационным полем g или их связанными потенциалами. Массу иногда называют «гравитационным зарядом». [18]
Электростатические и гравитационные силы являются центральными , консервативными и подчиняются закону обратных квадратов .
Равномерные поля
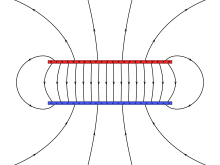
Однородное поле — это поле, в котором электрическое поле постоянно в каждой точке. Его можно аппроксимировать, поместив две проводящие пластины параллельно друг другу и поддерживая напряжение (разность потенциалов) между ними; это лишь аппроксимация из-за граничных эффектов (вблизи края плоскостей электрическое поле искажается, поскольку плоскость не продолжается). Предполагая бесконечные плоскости, величина электрического поля E равна: где Δ V — разность потенциалов между пластинами, а d — расстояние между пластинами. Отрицательный знак возникает, когда положительные заряды отталкиваются, поэтому положительный заряд будет испытывать силу, направленную от положительно заряженной пластины в противоположном направлении от того, в котором увеличивается напряжение. В микро- и наноприложениях, например, в отношении полупроводников, типичная величина электрического поля имеет порядок10 6 В⋅м −1 , достигаемое путем приложения напряжения порядка 1 вольта между проводниками, расположенными на расстоянии 1 мкм друг от друга.
Электромагнитные поля
Электромагнитные поля — это электрические и магнитные поля, которые могут изменяться со временем, например, когда заряды находятся в движении. Движущиеся заряды создают магнитное поле в соответствии с законом Ампера ( с добавлением Максвелла ), который вместе с другими уравнениями Максвелла определяет магнитное поле, , в терминах его ротора: где — плотность тока , — проницаемость вакуума , — диэлектрическая проницаемость вакуума .
Как плотность электрического тока , так и частная производная электрического поля по времени вносят вклад в ротор магнитного поля. Кроме того, уравнения Максвелла-Фарадея заявляют следующее. Они представляют собой два из четырех уравнений Максвелла , и они сложным образом связывают вместе электрические и магнитные поля, что приводит к электромагнитному полю . Уравнения представляют собой набор из четырех связанных многомерных уравнений в частных производных, которые при решении для системы описывают комбинированное поведение электромагнитных полей. В общем случае сила, испытываемая пробным зарядом в электромагнитном поле, задается законом силы Лоренца :
Энергия в электрическом поле
Полная энергия на единицу объема, запасенная электромагнитным полем, равна [19] где ε — диэлектрическая проницаемость среды, в которой существует поле, ее магнитная проницаемость , а E и B — векторы электрического и магнитного поля.
Поскольку поля E и B связаны, было бы ошибочно разделять это выражение на «электрические» и «магнитные» вклады. В частности, электростатическое поле в любой заданной системе отсчета в общем случае преобразуется в поле с магнитной составляющей в относительно движущейся системе отсчета. Соответственно, разложение электромагнитного поля на электрическую и магнитную составляющую является специфическим для системы отсчета, и аналогично для связанной энергии.
Полная энергия U EM, запасенная в электромагнитном поле в заданном объеме V, равна
Электрическое поле смещения
Окончательное уравнение векторных полей
При наличии материи полезно расширить понятие электрического поля до трех векторных полей: [20] где P — электрическая поляризация — объемная плотность электрических дипольных моментов , а D — электрическое поле смещения . Поскольку E и P определяются отдельно, это уравнение можно использовать для определения D. Физическая интерпретация D не так ясна, как E (фактически поле, приложенное к материалу) или P (индуцированное поле из-за диполей в материале), но все же служит удобным математическим упрощением, поскольку уравнения Максвелла можно упростить в терминах свободных зарядов и токов .
Конститутивное отношение
Поля E и D связаны диэлектрической проницаемостью материала ε . [21] [20]
Для линейных, однородных , изотропных материалов E и D пропорциональны и постоянны во всей области, зависимость от положения отсутствует:
Для неоднородных материалов существует позиционная зависимость по всему материалу: [22]
Для анизотропных материалов поля E и D не параллельны, поэтому E и D связаны тензором диэлектрической проницаемости ( тензорное поле 2-го порядка ) в компонентной форме:
Для нелинейных сред E и D не пропорциональны. Материалы могут иметь различную степень линейности, однородности и изотропности.
Релятивистские эффекты в электрическом поле
Точечный заряд в равномерном движении
Инвариантность формы уравнений Максвелла относительно преобразования Лоренца может быть использована для вывода электрического поля равномерно движущегося точечного заряда. Заряд частицы считается инвариантным относительно системы отсчета, что подтверждается экспериментальными данными. [23] В качестве альтернативы электрическое поле равномерно движущихся точечных зарядов может быть выведено из преобразования Лоренца четырех сил, испытываемых пробными зарядами в системе покоя источника, заданной законом Кулона , и назначения электрического поля и магнитного поля по их определению, заданному формой силы Лоренца . [24] Однако следующее уравнение применимо только тогда, когда в истории частицы нет ускорения, когда можно рассмотреть закон Кулона или использовать аргументы симметрии для решения уравнений Максвелла простым способом. Электрическое поле такого равномерно движущегося точечного заряда, следовательно, определяется выражением: [25] где — заряд точечного источника, — радиус-вектор от точечного источника до точки в пространстве, — отношение наблюдаемой скорости заряженной частицы к скорости света, а — угол между и наблюдаемой скоростью заряженной частицы.
Вышеуказанное уравнение сводится к уравнению, заданному законом Кулона для нерелятивистских скоростей точечного заряда. Сферическая симметрия не выполняется из-за нарушения симметрии в задаче путем указания направления скорости для расчета поля. Чтобы проиллюстрировать это, линии поля движущихся зарядов иногда представляются как неравномерно расположенные радиальные линии, которые будут казаться равноотстоящими в сопутствующей системе отсчета. [23]
Распространение возмущений в электрических полях
Специальная теория относительности навязывает принцип локальности , который требует, чтобы причина и следствие были разделенными во времени событиями, где причинная эффективность не распространяется быстрее скорости света . [26] Законы Максвелла подтверждают эту точку зрения, поскольку общие решения полей даются в терминах замедленного времени, что указывает на то, что электромагнитные возмущения распространяются со скоростью света . Опережающее время, которое также обеспечивает решение для закона Максвелла, игнорируется как нефизическое решение.

Для движения заряженной частицы , рассматривая, например, случай движущейся частицы с описанным выше электрическим полем, приходящей к резкой остановке, электрические поля в точках, далеких от нее, не немедленно возвращаются к классически заданному для неподвижного заряда. При остановке поле вокруг неподвижных точек начинает возвращаться к ожидаемому состоянию, и этот эффект распространяется наружу со скоростью света , в то время как линии электрического поля вдали от этого будут продолжать указывать радиально к предполагаемому движущемуся заряду. Эта виртуальная частица никогда не будет вне области распространения возмущения в электромагнитном поле , поскольку заряженные частицы ограничены иметь скорости, меньшие скорости света, что делает невозможным построение гауссовой поверхности в этой области, которая нарушает закон Гаусса . Другая техническая трудность, которая поддерживает это, заключается в том, что заряженные частицы, движущиеся быстрее или равные скорости света, больше не имеют уникального времени задержки. Поскольку линии электрического поля непрерывны, генерируется электромагнитный импульс излучения, который соединяется на границе этого возмущения, движущегося наружу со скоростью света . [27] В общем случае любой ускоряющийся точечный заряд излучает электромагнитные волны , однако в системах зарядов возможно и неизлучающее ускорение .
Произвольно движущийся точечный заряд
Для произвольно движущихся точечных зарядов распространение потенциальных полей, таких как калибровочные поля Лоренца со скоростью света, необходимо учитывать с помощью потенциала Льенара–Вихерта . [28] Поскольку потенциалы удовлетворяют уравнениям Максвелла , поля, полученные для точечного заряда, также удовлетворяют уравнениям Максвелла . Электрическое поле выражается как: [29] где — заряд точечного источника, — запаздывающее время или время, в которое возник вклад источника в электрическое поле, — радиус-вектор частицы, — единичный вектор, направленный от заряженной частицы к точке в пространстве, — скорость частицы, деленная на скорость света, — соответствующий фактор Лоренца . Запаздывающее время дается как решение:
Единственность решения для для заданных , и справедлива для заряженных частиц, движущихся медленнее скорости света. Известно, что электромагнитное излучение ускоряющихся зарядов вызвано членом, зависящим от ускорения в электрическом поле, из которого получается релятивистская поправка к формуле Лармора . [29]
Существует еще один набор решений для уравнения Максвелла той же формы, но для опережающего времени вместо запаздывающего, заданный как решение:
Поскольку физическая интерпретация этого указывает на то, что электрическое поле в точке управляется состоянием частицы в точке времени в будущем, оно рассматривается как нефизическое решение и, следовательно, игнорируется. Однако существуют теории, исследующие продвинутые временные решения уравнений Максвелла , такие как теория поглотителя Фейнмана-Уиллера .
Приведенное выше уравнение, хотя и согласуется с уравнением равномерно движущихся точечных зарядов, а также с его нерелятивистским пределом, не учитывает квантово-механические эффекты.
Общие формулы
Электрическое поле, бесконечно близкое к проводящей поверхности в электростатическом равновесии, имеющей плотность заряда в этой точке, так как заряды формируются только на поверхности, а поверхность в бесконечно малом масштабе напоминает бесконечную двумерную плоскость. При отсутствии внешних полей сферические проводники демонстрируют равномерное распределение заряда на поверхности и, следовательно, имеют такое же электрическое поле, как и равномерное распределение сферической поверхности.
Смотрите также
- Классический электромагнетизм
- Релятивистский электромагнетизм
- Электричество
- История электромагнитной теории
- Электромагнитное поле
- Магнетизм
- Телтронная трубка
- Teledeltos , проводящая бумага, которая может быть использована как простой аналоговый компьютер для моделирования полей.
Ссылки
- ^ Рош, Джон (2016). «Введение в электрические поля». Физическое образование . 51 (5): 055005. Bibcode : 2016PhyEd..51e5005R. doi : 10.1088/0031-9120/51/5/055005. S2CID 125014664.
- ^ Фейнман, Ричард (1970). Лекции Фейнмана по физике, том II. Эддисон Уэсли Лонгман. стр. 1–3, 1–4. ISBN 978-0-201-02115-8.
- ^ Перселл, Эдвард М.; Морин, Дэвид Дж. (2013).Электричество и магнетизм(3-е изд.). Нью-Йорк: Cambridge University Press. С. 15–16. ISBN 978-1-107-01402-2.
- ^ abc Serway, Raymond A.; Vuille, Chris (2014). College Physics (10-е изд.). Cengage Learning. стр. 532–533. ISBN 978-1305142824.
- ^ Международная система единиц (PDF) (9-е изд.), Международное бюро мер и весов, декабрь 2022 г., ISBN 978-92-822-2272-0, стр. 23
- ^ abc Сирс, Фрэнсис; и др. (1982), Университетская физика (6-е изд.), Аддисон Уэсли, ISBN 0-201-07199-1
- ^ Умашанкар, Корада (1989), Введение в инженерные электромагнитные поля , World Scientific, стр. 77–79, ISBN 9971-5-0921-0
- ^ ab Morely & Hughes (1970), Principles of Electricity (5-е изд.), Longman, стр. 73, ISBN 0-582-42629-4
- ^ Ту, Стивен (2011). Визуализация полей и приложений в инженерии. John Wiley and Sons. стр. 64. ISBN 9780470978467.
- ^ abc Гриффитс, Дэвид Дж. (1999). Введение в электродинамику (3-е изд.). Upper Saddle River, NJ: Prentice Hall. ISBN 0-13-805326-X. OCLC 40251748.
- ↑ Перселл, стр. 25: «Закон Гаусса: поток электрического поля E через любую замкнутую поверхность... равен 1/ e , умноженному на полный заряд, заключенный на поверхности».
- ↑ Перселл, стр. 356: «Закон индукции Фарадея».
- ^ Перселл, стр. 7: «... взаимодействие между покоящимися электрическими зарядами описывается законом Кулона: два неподвижных электрических заряда отталкиваются или притягиваются друг к другу с силой, пропорциональной произведению величин зарядов и обратно пропорциональной квадрату расстояния между ними».
- ^ Перселл, Эдвард (2011). Электричество и магнетизм (2-е изд.). Cambridge University Press. С. 8–9. ISBN 978-1139503556.
- ^ gwrowe (8 октября 2011 г.). "Curl & Potential in Electrostatics" (PDF) . physicspages.com . Архивировано из оригинала (PDF) 22 марта 2019 г. . Получено 2 ноября 2020 г. .
- ^ Huray, Paul G. (2009). Уравнения Максвелла. Wiley-IEEE. стр. 205. ISBN 978-0-470-54276-7.[ постоянная мертвая ссылка ]
- ↑ Перселл, стр. 5–7.
- ↑ Салам, Абдус (16 декабря 1976 г.). «Кварки и лептоны выходят играть». New Scientist . 72 : 652.[ постоянная мертвая ссылка ]
- ^ Гриффитс, DJ (2017). Введение в электродинамику (3-е изд.). Cambridge University Press. стр. 357, ур. 8.5. ISBN 9781108420419.
- ^ ab Грант, И.С.; Филлипс, В.Р. (2008). Электромагнетизм (2-е изд.). John Wiley & Sons. ISBN 978-0-471-92712-9.
- ^ Беннет, ГАГ; Арнольд, Эдвард (1974). Электричество и современная физика (2-е изд.). Эдвард Арнольд. ISBN 0-7131-2459-8.
- ^ Ландау, Лев Давидович ; Лифшиц, Евгений М. (1963). "68 распространение волн в неоднородной среде". Электродинамика сплошных сред. Курс теоретической физики . Т. 8. Пергам. С. 285. ISBN 978-0-7581-6499-5.
В уравнениях Максвелла… ε является функцией координат.
- ^ ab Purcell, Edward M.; Morin, David J. (2013-01-21). Электричество и магнетизм. стр. 241–251. doi :10.1017/cbo9781139012973. ISBN 9781139012973. Получено 2022-07-04 .
{{cite book}}:|website=проигнорировано ( помощь ) - ^ Россер, WGV (1968). Классический электромагнетизм через теорию относительности. С. 29–42. doi :10.1007/978-1-4899-6559-2. ISBN 978-1-4899-6258-4.
- ^ Хевисайд, Оливер. Электромагнитные волны, распространение потенциала и электромагнитные эффекты движущегося заряда.
- ^ Набер, Грегори Л. (2012). Геометрия пространства-времени Минковского: введение в математику специальной теории относительности . Springer. С. 4–5. ISBN 978-1-4419-7837-0. OCLC 804823303.
- ^ Перселл, Эдвард М.; Дэвид Дж. Морин (2013). Электричество и магнетизм (Третье изд.). Кембридж. С. 251–255. ISBN 978-1-139-01297-3. OCLC 1105718330.
{{cite book}}: CS1 maint: location missing publisher (link) - ^ Гриффитс, Дэвид Дж. (2017). Введение в электродинамику (4-е изд.). Соединенное Королевство: Cambridge University Press . стр. 454. ISBN 978-1-108-42041-9. OCLC 1021068059.
- ^ ab Джексон, Джон Дэвид (1999). Классическая электродинамика (3-е изд.). Нью-Йорк: Wiley. С. 664–665. ISBN 0-471-30932-X. OCLC 38073290.
- Перселл, Эдвард; Морин, Дэвид (2013). Электричество и магнетизм (3-е изд.). Cambridge University Press, Нью-Йорк. ISBN 978-1-107-01402-2.
- Браун, Майкл (2011). Физика для инженерии и науки (2-е изд.). McGraw-Hill, Шаум, Нью-Йорк. ISBN 978-0-07-161399-6.
Внешние ссылки
- Электрическое поле в «Электричестве и магнетизме», Р. Нейв – Гиперфизика , Университет штата Джорджия
- Лекции Фрэнка Вольфса в Рочестерском университете , главы 23 и 24
- Поля, архив 2010-05-27 в Wayback Machine – глава из онлайн-учебника















































































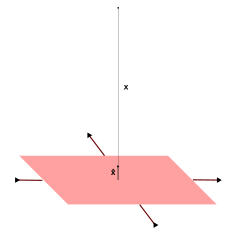










![{\displaystyle \mathbf {E} ={\frac {\sigma }{2\varepsilon _{0}}}\left[1-{\frac {x}{\sqrt {x^{2}+R^{2}}}}\right]{\hat {\mathbf {x} }},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6846763e54d7afcc4b7823929fd0a8993d9dbf49)