Скорость света
 | |
| Точное значение | |
|---|---|
| метров в секунду | 299 792 458 |
| Приблизительные значения (до трех значащих цифр) | |
| километров в час | 1 080 000 000 |
| миль в секунду | 186 000 |
| миль в час [1] | 671 000 000 |
| астрономических единиц в день | 173 [Примечание 1] |
| парсеков в год | 0,307 [Примечание 2] |
| Приблизительное время прохождения светового сигнала | |
| Расстояние | Время |
| одна нога | 1,0 нс |
| один метр | 3,3 нс |
| с геостационарной орбиты на Землю | 119 мс |
| длина экватора Земли | 134 мс |
| с Луны на Землю | 1,3 с |
| от Солнца до Земли (1 а.е. ) | 8.3 мин. |
| один световой год | 1.0 год |
| один парсек | 3,26 года |
| от ближайшей к Солнцу звезды (1.3 шт .) | 4,2 года |
| из ближайшей к Земле галактики | 70 000 лет |
| через Млечный Путь | 87 400 лет |
| от галактики Андромеды до Земли | 2,5 миллиона лет |
| Специальная теория относительности |
|---|
 |
Скорость света в вакууме , обычно обозначаемая как c , является универсальной физической константой , которая в точности равна 299 792 458 метров в секунду (приблизительно 300 000 километров в секунду; 186 000 миль в секунду; 671 миллион миль в час). [Примечание 3] Согласно специальной теории относительности , c является верхним пределом скорости, с которой обычная материя или энергия (и, следовательно, любой сигнал, несущий информацию ) может перемещаться в пространстве . [4] [5] [6]
Все формы электромагнитного излучения , включая видимый свет , движутся со скоростью света. Для многих практических целей свет и другие электромагнитные волны будут казаться распространяющимися мгновенно, но для больших расстояний и очень чувствительных измерений их конечная скорость имеет заметные эффекты. Большая часть звездного света, наблюдаемого на Земле, принадлежит далекому прошлому, что позволяет людям изучать историю Вселенной, наблюдая за удаленными объектами. При общении с далекими космическими зондами передача сигналов может занять от нескольких минут до нескольких часов. В вычислениях скорость света фиксирует минимальную задержку связи . Скорость света может использоваться при измерениях времени полета для измерения больших расстояний с чрезвычайно высокой точностью.
Оле Рёмер впервые продемонстрировал в 1676 году , что свет не распространяется мгновенно, изучая видимое движение спутника Юпитера Ио . В последующие столетия появлялись все более точные измерения его скорости. В статье, опубликованной в 1865 году, Джеймс Клерк Максвелл предположил, что свет является электромагнитной волной и, следовательно, распространяется со скоростью c . [7] В 1905 году Альберт Эйнштейн постулировал, что скорость света c относительно любой инерциальной системы отсчета является постоянной и не зависит от движения источника света. [8] Он исследовал последствия этого постулата, выведя теорию относительности , и, сделав это, показал, что параметр c имеет значение вне контекста света и электромагнетизма.
Безмассовые частицы и возмущения поля , такие как гравитационные волны , также движутся со скоростью c в вакууме. Такие частицы и волны движутся со скоростью c независимо от движения источника или инерциальной системы отсчета наблюдателя . Частицы с ненулевой массой покоя могут быть ускорены до c, но никогда не смогут достичь ее, независимо от системы отсчета, в которой измеряется их скорость. В теории относительности c связывает пространство и время и появляется в знаменитой эквивалентности массы и энергии , E = mc 2 . [9]
В некоторых случаях может показаться, что объекты или волны движутся быстрее света (например, фазовые скорости волн, появление некоторых высокоскоростных астрономических объектов и определенные квантовые эффекты ). Расширение Вселенной, как предполагается, превышает скорость света за определенной границей .
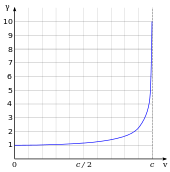
Скорость, с которой свет распространяется через прозрачные материалы , такие как стекло или воздух, меньше c ; аналогично, скорость электромагнитных волн в проводах меньше c . Отношение между c и скоростью v , с которой свет распространяется в материале, называется показателем преломления n материала ( n = с/в ). Например, для видимого света показатель преломления стекла обычно составляет около 1,5, что означает, что свет в стекле распространяется со скоростью с/1.5 ≈ 200 000 км/с ( 124 000 миль/с) ; показатель преломления воздуха для видимого света составляет около 1,0003, поэтому скорость света в воздухе примерно на 90 км/с (56 миль/с) меньше, чем c .
Числовое значение, обозначение и единицы измерения
Скорость света в вакууме обычно обозначается строчной буквой c , что означает «константа» или латинское celeritas (что означает «быстрота, стремительность»). В 1856 году Вильгельм Эдуард Вебер и Рудольф Кольрауш использовали c для другой константы, которая, как позже было показано, равна √ 2 скорости света в вакууме. Исторически символ V использовался как альтернативный символ для скорости света, введенный Джеймсом Клерком Максвеллом в 1865 году. В 1894 году Пауль Друде переопределил c, придав ему современное значение. Эйнштейн использовал V в своих оригинальных немецкоязычных статьях по специальной теории относительности в 1905 году, но в 1907 году он перешел на c , который к тому времени стал стандартным символом для скорости света. [10] [11]
Иногда c используется для скорости волн в любой материальной среде, а c 0 — для скорости света в вакууме. [12] Эта подстрочная нотация, которая одобрена в официальной литературе СИ, [13] имеет ту же форму, что и связанные электромагнитные константы: а именно, μ 0 для проницаемости вакуума или магнитной постоянной, ε 0 для диэлектрической проницаемости вакуума или электрической постоянной и Z 0 для импеданса свободного пространства . В этой статье c используется исключительно для скорости света в вакууме.
Использование в системах единиц
С 1983 года константа c была определена в Международной системе единиц (СИ) как 299 792 458 м/с ; это соотношение используется для определения метра как точного расстояния, которое свет проходит в вакууме за 1 ⁄299 792 458 секунды. Используя значение c , а также точное измерение секунды,можно таким образом установить стандарт для метра.[14]Какразмерная физическая константа, численное значение c различно для разных систем единиц. Например, вимперскихединицахскорость света приблизительно равна186 282 миль в секунду, [Примечание 4] или примерно 1 фут в наносекунду. [Примечание 5] [15] [16]
В разделах физики, где c часто появляется, например, в теории относительности, принято использовать системы естественных единиц измерения или геометризированную систему единиц , где c = 1. [17] [18] При использовании этих единиц c не появляется явно, поскольку умножение или деление на 1 не влияет на результат. Его единица измерения световая секунда в секунду по-прежнему актуальна, даже если опущена.
Фундаментальная роль в физике
Скорость, с которой световые волны распространяются в вакууме, не зависит ни от движения источника волн, ни от инерциальной системы отсчета наблюдателя. [Примечание 6] Эта инвариантность скорости света была постулирована Эйнштейном в 1905 году [8] , после того как он был мотивирован теорией электромагнетизма Максвелла и отсутствием доказательств движения против светоносного эфира . [19] С тех пор это последовательно подтверждалось многими экспериментами. [Примечание 7] Экспериментально можно проверить только то, что двусторонняя скорость света (например, от источника к зеркалу и обратно) не зависит от системы отсчета, поскольку невозможно измерить одностороннюю скорость света (например, от источника к удаленному детектору) без некоторой договоренности о том, как должны быть синхронизированы часы в источнике и на детекторе. [20] [21]
Принимая синхронизацию Эйнштейна для часов, односторонняя скорость света становится равной двусторонней скорости света по определению. [20] [21] Специальная теория относительности исследует последствия этой инвариантности c , предполагая, что законы физики одинаковы во всех инерциальных системах отсчета. [22] [23] Одним из следствий является то, что c — это скорость, с которой все безмассовые частицы и волны, включая свет, должны перемещаться в вакууме. [24] [Примечание 8]
Специальная теория относительности имеет много контринтуитивных и экспериментально подтвержденных следствий. [26] К ним относятся эквивалентность массы и энергии ( E = mc2 ) , сокращение длины (движущиеся объекты укорачиваются), [Примечание 9] и замедление времени (движущиеся часы идут медленнее). Фактор γ, на который сокращаются длины и замедляется время, известен как фактор Лоренца и определяется как γ = (1 − v2 / c2 ) −1/2 , где v — скорость объекта. Отличие γ от 1 пренебрежимо мало для скоростей, намного меньших, чем c , таких как большинство повседневных скоростей — в этом случае специальная теория относительности близко аппроксимируется галилеевой теорией относительности — но оно увеличивается на релятивистских скоростях и расходится до бесконечности, когда v приближается к c . Например, фактор замедления времени γ = 2 возникает при относительной скорости 86,6% скорости света ( v = 0,866 c ). Аналогично, фактор замедления времени γ = 10 возникает при 99,5% скорости света ( v = 0,995 c ).
Результаты специальной теории относительности можно суммировать, рассматривая пространство и время как единую структуру, известную как пространство-время (с c, связывающим единицы пространства и времени), и требуя, чтобы физические теории удовлетворяли специальной симметрии, называемой лоренц-инвариантностью , математическая формулировка которой содержит параметр c . [29] Лоренц-инвариантность является почти универсальным предположением для современных физических теорий, таких как квантовая электродинамика , квантовая хромодинамика , Стандартная модель физики элементарных частиц и общая теория относительности . Таким образом, параметр c повсеместно встречается в современной физике, появляясь во многих контекстах, не связанных со светом. Например, общая теория относительности предсказывает, что c также является скоростью гравитации и гравитационных волн , [30] и наблюдения гравитационных волн согласуются с этим предсказанием. [31] В неинерциальных системах отсчета (гравитационно искривленном пространстве-времени или ускоренных системах отсчета ) локальная скорость света постоянна и равна c , но скорость света может отличаться от c при измерении из удаленной системы отсчета, в зависимости от того, как измерения экстраполируются на регион. [32]
Обычно предполагается, что фундаментальные константы, такие как c, имеют одинаковое значение во всем пространстве-времени, что означает, что они не зависят от местоположения и не меняются со временем. Однако в различных теориях предполагалось, что скорость света могла меняться с течением времени . [33] [34] Не было найдено никаких убедительных доказательств таких изменений, но они остаются предметом продолжающихся исследований. [35] [36]
Обычно предполагается, что двусторонняя скорость света изотропна , что означает, что она имеет одно и то же значение независимо от направления, в котором она измеряется. Наблюдения за излучением ядерных энергетических уровней в зависимости от ориентации излучающих ядер в магнитном поле (см. эксперимент Хьюза-Древера ) и вращающихся оптических резонаторов (см. эксперименты с резонаторами ) наложили строгие ограничения на возможную двустороннюю анизотропию . [37] [38]
Верхний предел скорости
Согласно специальной теории относительности, энергия объекта с массой покоя m и скоростью v определяется как γmc 2 , где γ — фактор Лоренца, определенный выше. Когда v равно нулю, γ равно единице, что приводит к знаменитой формуле E = mc 2 для эквивалентности массы и энергии. Фактор γ стремится к бесконечности, когда v приближается к c , и потребовалось бы бесконечное количество энергии, чтобы разогнать объект с массой до скорости света. Скорость света является верхним пределом для скоростей объектов с положительной массой покоя, и отдельные фотоны не могут двигаться быстрее скорости света. [39] Это экспериментально установлено во многих тестах релятивистской энергии и импульса . [40]

В более общем смысле, сигналы или энергия не могут перемещаться быстрее, чем c . Один из аргументов в пользу этого следует из контринтуитивного следствия специальной теории относительности, известного как относительность одновременности . Если пространственное расстояние между двумя событиями A и B больше, чем временной интервал между ними, умноженный на c, то существуют системы отсчета, в которых A предшествует B, другие, в которых B предшествует A, и третьи, в которых они одновременны. В результате, если бы что-то перемещалось быстрее, чем c относительно инерциальной системы отсчета, оно перемещалось бы назад во времени относительно другой системы, и причинность была бы нарушена. [Примечание 10] [43] В такой системе отсчета «следствие» можно было бы наблюдать раньше его «причины». Такое нарушение причинности никогда не было зафиксировано, [21] и привело бы к парадоксам, таким как тахионный антителефон . [44]
Наблюдения и эксперименты со сверхсветовыми скоростями
Существуют ситуации, в которых может показаться, что материя, энергия или сигнал, несущий информацию, движутся со скоростью, превышающей c , но это не так. Например, как обсуждается в разделе «Распространение света в среде» ниже, многие скорости волн могут превышать c . Фазовая скорость рентгеновских лучей через большинство стекол может обычно превышать c , [45] но фазовая скорость не определяет скорость, с которой волны передают информацию. [46]
Если лазерный луч быстро проносится по удаленному объекту, пятно света может двигаться быстрее, чем c , хотя первоначальное движение пятна задерживается из-за времени, которое требуется свету, чтобы добраться до удаленного объекта со скоростью c . Однако единственными физическими сущностями, которые движутся, являются лазер и излучаемый им свет, который движется со скоростью c от лазера к различным положениям пятна. Аналогично, тень, спроецированная на удаленный объект, может двигаться быстрее, чем c , после задержки во времени. [47] Ни в том, ни в другом случае никакая материя, энергия или информация не движутся быстрее света. [48]
Скорость изменения расстояния между двумя объектами в системе отсчета, относительно которой оба движутся (их скорость сближения ), может иметь значение, превышающее c . Однако это не отражает скорость любого отдельного объекта, измеренную в одной инерциальной системе отсчета. [48]
Некоторые квантовые эффекты, по-видимому, передаются мгновенно и, следовательно, быстрее, чем c , как в парадоксе ЭПР . Пример включает квантовые состояния двух частиц, которые могут быть запутаны . Пока одна из частиц не наблюдается, они существуют в суперпозиции двух квантовых состояний. Если частицы разделены и наблюдается квантовое состояние одной частицы, квантовое состояние другой частицы определяется мгновенно. Однако невозможно контролировать, какое квантовое состояние примет первая частица, когда она наблюдается, поэтому информация не может быть передана таким образом. [48] [49]
Другой квантовый эффект, который предсказывает возникновение скоростей, превышающих скорость света, называется эффектом Хартмана : при определенных условиях время, необходимое виртуальной частице для туннелирования через барьер, постоянно, независимо от толщины барьера. [50] [51] Это может привести к тому, что виртуальная частица пересечет большой зазор быстрее света. Однако с помощью этого эффекта нельзя отправить никакую информацию. [52]
Так называемое сверхсветовое движение наблюдается в некоторых астрономических объектах, [53] таких как релятивистские струи радиогалактик и квазаров . Однако эти струи не движутся со скоростью, превышающей скорость света: видимое сверхсветовое движение является проекционным эффектом, вызванным объектами , движущимися со скоростью, близкой к скорости света, и приближающимися к Земле под небольшим углом к лучу зрения: поскольку свет, который был испущен, когда струя была дальше, достигал Земли дольше, время между двумя последовательными наблюдениями соответствует более длительному времени между моментами испускания световых лучей. [54]
Эксперимент 2011 года, в ходе которого было обнаружено, что нейтрино движутся быстрее света, оказался следствием экспериментальной ошибки. [55] [56]
В моделях расширяющейся Вселенной , чем дальше галактики находятся друг от друга, тем быстрее они расходятся. Например, предполагается, что галактики, далекие от Земли, удаляются от Земли со скоростью, пропорциональной их расстоянию. За пределами границы, называемой сферой Хаббла , скорость, с которой увеличивается их расстояние от Земли, становится больше скорости света. [57] Эти скорости разбегания, определяемые как увеличение собственного расстояния за космологическое время , не являются скоростями в релятивистском смысле. Скорости космологического разбегания, превышающие скорость света, являются лишь артефактом координат .
Распространение света
В классической физике свет описывается как тип электромагнитной волны . Классическое поведение электромагнитного поля описывается уравнениями Максвелла , которые предсказывают, что скорость c , с которой электромагнитные волны (такие как свет) распространяются в вакууме, связана с распределенной емкостью и индуктивностью вакуума, иначе соответственно известными как электрическая постоянная ε 0 и магнитная постоянная μ 0 , уравнением [58]
В современной квантовой физике электромагнитное поле описывается теорией квантовой электродинамики (КЭД). В этой теории свет описывается фундаментальными возбуждениями (или квантами) электромагнитного поля, называемыми фотонами . В КЭД фотоны являются безмассовыми частицами и, таким образом, согласно специальной теории относительности, они движутся со скоростью света в вакууме. [24]
Были рассмотрены расширения КЭД, в которых фотон имеет массу. В такой теории его скорость зависела бы от его частоты, а инвариантная скорость c специальной теории относительности была бы тогда верхним пределом скорости света в вакууме. [32] Никакого изменения скорости света с частотой не наблюдалось при строгом тестировании, что накладывает строгие ограничения на массу фотона. [59] Полученный предел зависит от используемой модели: если массивный фотон описывается теорией Прока , [60] экспериментальная верхняя граница его массы составляет около 10−57 граммов ; [ 61] если масса фотона генерируется механизмом Хиггса , экспериментальный верхний предел менее резкий, m ≤10−14 эВ/ c2 ( примерно 2 × 10−47 г ) . [60]
Другой причиной изменения скорости света в зависимости от его частоты может быть невозможность применения специальной теории относительности к произвольно малым масштабам, как предсказывали некоторые предложенные теории квантовой гравитации . В 2009 году наблюдение за гамма-всплеском GRB 090510 не обнаружило никаких доказательств зависимости скорости фотона от энергии, что подтверждает жесткие ограничения в конкретных моделях квантования пространства-времени на то, как эта скорость зависит от энергии фотона для энергий, приближающихся к масштабу Планка . [62]
В среде
В среде свет обычно не распространяется со скоростью, равной c ; кроме того, различные типы световых волн будут распространяться с разной скоростью. Скорость, с которой распространяются отдельные гребни и впадины плоской волны (волны, заполняющей все пространство, только с одной частотой ), называется фазовой скоростью v p . Физический сигнал с конечной протяженностью (импульс света) распространяется с другой скоростью. Общая огибающая импульса распространяется с групповой скоростью v g , а его самая ранняя часть распространяется с фронтальной скоростью v f . [63]
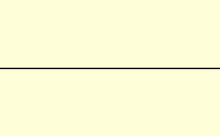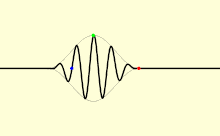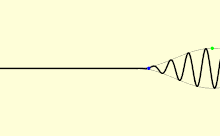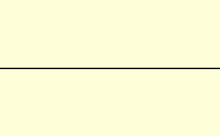
Фазовая скорость важна для определения того, как световая волна проходит через материал или из одного материала в другой. Она часто представлена в терминах показателя преломления . Показатель преломления материала определяется как отношение c к фазовой скорости v p в материале: большие показатели преломления указывают на более низкие скорости. Показатель преломления материала может зависеть от частоты света, интенсивности, поляризации или направления распространения; во многих случаях, однако, его можно рассматривать как константу, зависящую от материала. Показатель преломления воздуха составляет приблизительно 1,0003. [64] Более плотные среды, такие как вода , [65], стекло , [66] и алмаз , [67] имеют показатели преломления около 1,3, 1,5 и 2,4 соответственно для видимого света.
В экзотических материалах, таких как конденсаты Бозе-Эйнштейна вблизи абсолютного нуля, эффективная скорость света может составлять всего несколько метров в секунду. Однако это представляет собой задержку поглощения и повторного излучения между атомами, как и все скорости медленнее, чем c, в материальных субстанциях. В качестве экстремального примера «замедления» света в материи две независимые группы физиков заявили, что привели свет к «полной остановке», пропустив его через конденсат Бозе-Эйнштейна элемента рубидия . Популярное описание света, «остановленного» в этих экспериментах, относится только к свету, хранящемуся в возбужденных состояниях атомов, а затем повторно испускаемому в произвольное более позднее время, стимулируемому вторым лазерным импульсом. За время, пока он «останавливался», он перестал быть светом. Этот тип поведения, как правило, микроскопически верен для всех прозрачных сред, которые «замедляют» скорость света. [68]
В прозрачных материалах показатель преломления обычно больше 1, что означает, что фазовая скорость меньше c . В других материалах показатель преломления может стать меньше 1 для некоторых частот; в некоторых экзотических материалах показатель преломления может даже стать отрицательным. [69] Требование того, чтобы причинность не нарушалась, подразумевает, что действительная и мнимая части диэлектрической проницаемости любого материала, соответствующие соответственно показателю преломления и коэффициенту затухания , связаны соотношениями Крамерса-Кронига . [70] [71] На практике это означает, что в материале с показателем преломления меньше 1 волна будет быстро поглощаться. [72]
Импульс с различными групповыми и фазовыми скоростями (что происходит, если фазовая скорость не одинакова для всех частот импульса) размывается со временем, процесс, известный как дисперсия . Некоторые материалы имеют исключительно низкую (или даже нулевую) групповую скорость для световых волн, явление, называемое медленным светом . [73] Противоположность, групповые скорости, превышающие c , были теоретически предложены в 1993 году и достигнуты экспериментально в 2000 году. [74] Групповая скорость должна даже быть возможной, чтобы стать бесконечной или отрицательной, с импульсами, перемещающимися мгновенно или назад во времени. [63]
Ни один из этих вариантов не позволяет передавать информацию быстрее, чем c . Невозможно передавать информацию с помощью светового импульса быстрее, чем скорость самой ранней части импульса (скорость фронта). Можно показать, что это (при определенных предположениях) всегда равно c . [63]
Частица может перемещаться через среду быстрее, чем фазовая скорость света в этой среде (но все еще медленнее, чем c ). Когда заряженная частица делает это в диэлектрическом материале, испускается электромагнитный эквивалент ударной волны , известный как излучение Черенкова . [75]
Практические эффекты конечности
Скорость света имеет значение для телекоммуникаций : время задержки в одну сторону и в оба конца больше нуля. Это применимо от малых до астрономических масштабов. С другой стороны, некоторые методы зависят от конечной скорости света, например, при измерении расстояний.
Мелкие весы
В компьютерах скорость света накладывает ограничение на то, как быстро данные могут быть переданы между процессорами . Если процессор работает на частоте 1 гигагерц , сигнал может пройти максимум около 30 сантиметров (1 фут) за один тактовый цикл — на практике это расстояние еще короче, поскольку печатная плата преломляет и замедляет сигналы. Поэтому процессоры должны быть размещены близко друг к другу, как и чипы памяти , чтобы минимизировать задержки связи, и необходимо проявлять осторожность при прокладке проводов между ними, чтобы обеспечить целостность сигнала . Если тактовые частоты продолжат расти, скорость света может в конечном итоге стать ограничивающим фактором для внутренней конструкции отдельных чипов . [76] [77]
Большие расстояния на Земле
Учитывая, что экваториальная окружность Земли составляет около40 075 км и что c составляет около300 000 км/с , теоретически кратчайшее время для передачи информации через половину земного шара по поверхности составляет около 67 миллисекунд. Когда свет движется по оптоволокну ( прозрачный материал ), фактическое время прохождения больше, отчасти потому, что скорость света в оптоволокне примерно на 35% ниже, в зависимости от его показателя преломления n . [Примечание 11] Прямые линии редки в глобальных коммуникациях, и время прохождения увеличивается, когда сигналы проходят через электронные переключатели или регенераторы сигналов. [79]
Хотя это расстояние в значительной степени не имеет значения для большинства приложений, задержка становится важной в таких областях, как высокочастотная торговля , где трейдеры стремятся получить минутные преимущества, доставляя свои сделки на биржи на доли секунды раньше других трейдеров. Например, трейдеры переходят на микроволновую связь между торговыми центрами из-за преимущества, которое радиоволны, распространяющиеся со скоростью, близкой к скорости света по воздуху, имеют по сравнению со сравнительно медленными оптоволоконными сигналами. [80] [81]
Космические полеты и астрономия

Аналогично, связь между Землей и космическим кораблем не мгновенна. Существует кратковременная задержка от источника до приемника, которая становится более заметной по мере увеличения расстояния. Эта задержка была существенной для связи между наземным управлением и Аполлоном-8 , когда он стал первым пилотируемым космическим кораблем, вышедшим на орбиту Луны : на каждый вопрос наземная станция управления должна была ждать ответа не менее трех секунд. [82]
Задержка связи между Землей и Марсом может варьироваться от пяти до двадцати минут в зависимости от относительного положения двух планет. Вследствие этого, если робот на поверхности Марса столкнется с проблемой, его человеческие контроллеры не будут знать об этом, пока не пройдет примерно 4–24 минуты . Затем потребуется еще 4–24 минуты , чтобы команды переместились с Земли на Марс. [83] [84]
Прием света и других сигналов от далеких астрономических источников занимает гораздо больше времени. Например, требуется 13 миллиардов (13 × 109 ) лет, необходимых свету для путешествия до Земли от далеких галактик, наблюдаемых на снимках Hubble Ultra-Deep Field . [85] [86] Эти фотографии, сделанные сегодня, запечатлели изображения галактик, какими они были 13 миллиардов лет назад, когда Вселенной было менее миллиарда лет. [85] Тот факт, что более далекие объекты кажутся моложе из-за конечной скорости света, позволяет астрономам делать выводы об эволюции звезд , галактик и самой Вселенной . [87]
Астрономические расстояния иногда выражаются в световых годах , особенно в научно-популярных публикациях и средствах массовой информации. [88] Световой год — это расстояние, которое свет проходит за один юлианский год , около 9461 миллиарда километров, 5879 миллиардов миль или 0,3066 парсека . Округленно, световой год составляет около 10 триллионов километров или около 6 триллионов миль. Проксима Центавра , ближайшая к Земле звезда после Солнца, находится на расстоянии около 4,2 световых лет. [89]
Измерение расстояния
Радарные системы измеряют расстояние до цели по времени, которое требуется радиоволновому импульсу, чтобы вернуться к антенне радара после отражения от цели: расстояние до цели равно половине времени прохождения туда и обратно , умноженному на скорость света. Приемник Глобальной системы позиционирования (GPS) измеряет свое расстояние до спутников GPS на основе того, сколько времени требуется радиосигналу, чтобы прибыть от каждого спутника, и на основе этих расстояний вычисляет местоположение приемника. Поскольку свет распространяется примерно300 000 километров (186 000 миль ) за одну секунду, эти измерения малых долей секунды должны быть очень точными. Эксперимент по лазерной локации Луны , радиолокационная астрономия и Deep Space Network определяют расстояния до Луны, [90] планет [91] и космических аппаратов [92] соответственно, измеряя время прохождения туда и обратно.
Измерение
Существуют различные способы определения значения c . Один из способов — измерение фактической скорости распространения световых волн, что можно сделать в различных астрономических и наземных установках. Также возможно определить c из других физических законов, где оно появляется, например, определив значения электромагнитных констант ε 0 и μ 0 и используя их связь с c . Исторически наиболее точные результаты были получены путем отдельного определения частоты и длины волны светового луча, причем их произведение равно c . Это описано более подробно в разделе «Интерферометрия» ниже.
В 1983 году метр был определен как «длина пути, проходимого светом в вакууме за промежуток времени 1 ⁄299 792 458 секунды»,[93]фиксируя значение скорости света в299 792 458 м/с по определению, как описано ниже. Следовательно, точные измерения скорости света дают точную реализацию метра, а не точное значение c .
Астрономические измерения

Космос является удобным местом для измерения скорости света из-за его большого масштаба и почти идеального вакуума . Обычно измеряется время, необходимое свету для прохождения некоторого опорного расстояния в Солнечной системе , например радиуса орбиты Земли. Исторически такие измерения могли быть сделаны довольно точно по сравнению с тем, насколько точно известна длина опорного расстояния в земных единицах.
Оле Кристенсен Рёмер использовал астрономическое измерение, чтобы сделать первую количественную оценку скорости света в 1676 году. [94] [95] При измерении с Земли периоды обращения лун вокруг далекой планеты короче, когда Земля приближается к планете, чем когда Земля удаляется от нее. Разница невелика, но совокупное время становится значительным при измерении в течение месяцев. Расстояние, пройденное светом от планеты (или ее луны) до Земли, короче, когда Земля находится в точке своей орбиты, которая ближе всего к ее планете, чем когда Земля находится в самой дальней точке своей орбиты, причем разница в расстоянии равна диаметру орбиты Земли вокруг Солнца. Наблюдаемое изменение орбитального периода луны вызвано разницей во времени, которое требуется свету для прохождения более короткого или более длинного расстояния. Рёмер наблюдал этот эффект для самого внутреннего большого спутника Юпитера Ио и пришел к выводу, что свету требуется 22 минуты, чтобы пересечь диаметр орбиты Земли. [94]

Другой метод заключается в использовании аберрации света , открытой и объясненной Джеймсом Брэдли в 18 веке. [96] Этот эффект возникает в результате векторного сложения скорости света, прибывающего из удаленного источника (например, звезды), и скорости его наблюдателя (см. диаграмму справа). Таким образом, движущийся наблюдатель видит свет, приходящий с немного другого направления, и, следовательно, видит источник в положении, смещенном от его первоначального положения. Поскольку направление скорости Земли непрерывно меняется по мере того, как Земля вращается вокруг Солнца, этот эффект заставляет видимое положение звезд смещаться. Из угловой разницы в положении звезд (максимум 20,5 угловых секунд ) [97] можно выразить скорость света через скорость Земли вокруг Солнца, которую при известной длине года можно преобразовать во время, необходимое для путешествия от Солнца до Земли. В 1729 году Брэдли использовал этот метод, чтобы вывести, что свет прошелВ 10 210 раз быстрее Земли на ее орбите (современная цифра составляетв 10 066 раз быстрее) или, что то же самое, что свету потребуется 8 минут 12 секунд, чтобы пройти путь от Солнца до Земли. [96]
Астрономическая единица
Астрономическая единица ( AU) приблизительно равна среднему расстоянию между Землей и Солнцем. Она была переопределена в 2012 году как точно149 597 870 700 м . [98] [99] Ранее AU основывалась не на Международной системе единиц, а на гравитационной силе, оказываемой Солнцем в рамках классической механики. [Примечание 12] Текущее определение использует рекомендуемое значение в метрах для предыдущего определения астрономической единицы, которое было определено путем измерения. [98] Это переопределение аналогично переопределению метра и также имеет эффект фиксации скорости света на точном значении в астрономических единицах в секунду (через точную скорость света в метрах в секунду). [101]
Ранее обратная величина c, выраженная в секундах на астрономическую единицу, измерялась путем сравнения времени, необходимого радиосигналам для достижения различных космических аппаратов в Солнечной системе, с их положением, рассчитанным на основе гравитационных эффектов Солнца и различных планет. Объединив множество таких измерений, можно было получить наилучшее значение для светового времени на единицу расстояния. Например, в 2009 году наилучшая оценка, одобренная Международным астрономическим союзом (МАС), была: [102] [103]
- Время распространения света на единицу расстояния: t au = 499.004 783 836 (10) с ,
- с = 0,002 003 988 804 10 (4) ЕД/с = 173,144 632 674 (3) AU/d .
Относительная погрешность этих измерений составляет 0,02 части на миллиард (2 × 10−11 ), что эквивалентно неопределенности наземных измерений длины с помощью интерферометрии. [104] Поскольку метр определяется как длина, пройденная светом за определенный промежуток времени, измерение светового времени в терминах предыдущего определения астрономической единицы также может быть интерпретировано как измерение длины а.е. (старое определение) в метрах. [Примечание 13]
Методы измерения времени пролета

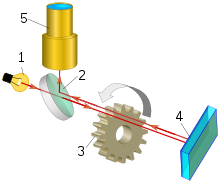
- Источник света
- Полупрозрачное светоделительное зеркало
- Зубчатое колесо-прерыватель светового луча
- Удаленное зеркало
- Телескопическая трубка
Метод измерения скорости света заключается в измерении времени, необходимого свету для прохождения до зеркала на известном расстоянии и обратно. Это рабочий принцип, лежащий в основе экспериментов Ипполита Физо и Леона Фуко .
Установка , которую использовал Физо, состоит из луча света, направленного на зеркало на расстоянии 8 километров (5 миль). На пути от источника к зеркалу луч проходит через вращающееся зубчатое колесо. При определенной скорости вращения луч проходит через один зазор на выходе и через другой на обратном пути, но при немного большей или меньшей скорости луч ударяется о зуб и не проходит через колесо. Зная расстояние между колесом и зеркалом, количество зубцов на колесе и скорость вращения, можно вычислить скорость света. [105]
Метод Фуко заменяет зубчатое колесо вращающимся зеркалом. Поскольку зеркало продолжает вращаться, пока свет движется к дальнему зеркалу и обратно, свет отражается от вращающегося зеркала под другим углом на своем пути наружу, чем на обратном пути. Из этой разницы в угле, известной скорости вращения и расстояния до дальнего зеркала можно вычислить скорость света. [106] Фуко использовал этот аппарат для измерения скорости света в воздухе по сравнению со скоростью света в воде, основываясь на предложении Франсуа Араго . [107]
Сегодня, используя осциллографы с временным разрешением менее одной наносекунды, скорость света можно измерить напрямую, засекая задержку светового импульса от лазера или светодиода, отраженного от зеркала. Этот метод менее точен (с погрешностью порядка 1%), чем другие современные методы, но иногда его используют в качестве лабораторного эксперимента на занятиях по физике в колледже. [108]
Электромагнитные константы
Вариантом вывода c , который напрямую не зависит от измерения распространения электромагнитных волн, является использование соотношения между c и диэлектрической проницаемостью вакуума ε 0 и проницаемостью вакуума μ 0 , установленного теорией Максвелла: c 2 = 1/( ε 0 μ 0 ). Диэлектрическая проницаемость вакуума может быть определена путем измерения емкости и размеров конденсатора , тогда как значение проницаемости вакуума исторически было зафиксировано на уровне точно4π × 10−7 Гн⋅м −1 через определение ампера . Роза и Дорси использовали этот метод в 1907 году , чтобы найти значение299 710 ± 22 км/с . Их метод зависел от наличия стандартной единицы электрического сопротивления, «международного ома », и поэтому его точность была ограничена тем, как этот стандарт был определен. [109] [110]
Резонанс полости

Другой способ измерения скорости света — независимое измерение частоты f и длины волны λ электромагнитной волны в вакууме. Значение c затем можно найти, используя соотношение c = fλ . Одним из вариантов является измерение резонансной частоты резонатора полости . Если размеры резонансной полости также известны, их можно использовать для определения длины волны волны. В 1946 году Луис Эссен и А. К. Гордон-Смит установили частоту для различных нормальных мод микроволн микроволновой полости точно известных размеров. Размеры были установлены с точностью около ±0,8 мкм с использованием датчиков, откалиброванных с помощью интерферометрии. [109] Поскольку длина волны мод была известна из геометрии полости и из электромагнитной теории , знание связанных частот позволило вычислить скорость света. [109] [111]
Результат Эссена–Гордона–Смита,299 792 ± 9 км/с , была существенно точнее, чем та, что была найдена оптическими методами. [109] К 1950 году повторные измерения Эссена установили результат299 792,5 ± 3,0 км/с . [112]
Возможна демонстрация этого метода в домашних условиях с использованием микроволновой печи и таких продуктов, как зефир или маргарин: если убрать поворотный стол так, чтобы еда не двигалась, она будет готовиться быстрее всего в пучностях ( точках, в которых амплитуда волны наибольшая), где она начнет плавиться. Расстояние между двумя такими точками составляет половину длины волны микроволн; измеряя это расстояние и умножая длину волны на частоту микроволн (обычно отображается на задней стенке печи, как правило, 2450 МГц), можно вычислить значение c , «часто с погрешностью менее 5%». [113] [114]
Интерферометрия

Интерферометрия — еще один метод определения длины волны электромагнитного излучения для определения скорости света. [Примечание 14] Когерентный луч света (например, от лазера ) с известной частотой ( f ) разделяется на два пути, а затем рекомбинируется. Регулируя длину пути, наблюдая за интерференционной картиной и тщательно измеряя изменение длины пути, можно определить длину волны света ( λ ). Затем скорость света вычисляется с помощью уравнения c = λf .
До появления лазерной технологии когерентные радиоисточники использовались для интерферометрических измерений скорости света. [116] Интерферометрическое определение длины волны становится менее точным с длиной волны, и поэтому эксперименты были ограничены по точности большой длиной волны (~4 мм (0,16 дюйма)) радиоволн. Точность может быть улучшена за счет использования света с более короткой длиной волны, но тогда становится трудно напрямую измерить частоту света. [117]
Один из способов обойти эту проблему — начать с низкочастотного сигнала, частоту которого можно точно измерить, и из этого сигнала постепенно синтезировать более высокочастотные сигналы, частоту которых можно затем связать с исходным сигналом. Затем лазер можно зафиксировать на частоте, а его длину волны можно определить с помощью интерферометрии. [117] Эта техника была разработана группой из Национального бюро стандартов (которое позже стало Национальным институтом стандартов и технологий ). Они использовали ее в 1972 году для измерения скорости света в вакууме с дробной неопределенностью3,5 × 10−9 . [117] [ 118]
История
До раннего современного периода не было известно, распространяется ли свет мгновенно или с очень высокой конечной скоростью. Первое сохранившееся письменное исследование этого предмета было в Древней Греции . Древние греки, арабские ученые и классические европейские ученые долго спорили об этом, пока Рёмер не предоставил первый расчет скорости света. Специальная теория относительности Эйнштейна постулирует, что скорость света постоянна независимо от системы отсчета. С тех пор ученые проводили все более точные измерения.
| <1638 | Галилео , крытые фонари | неокончательно [119] [120] [121] : 1252 [Примечание 15] | |
| <1667 | Accademia del Cimento , крытые фонари | неопределенно [121] : 1253 [122] | |
| 1675 | Рёмер и Гюйгенс — спутники Юпитера. | 220 000 000 [95] [123] | −27% |
| 1729 | Джеймс Брэдли , аберрация света | 301 000 000 [105] | +0,40% |
| 1849 | Ипполит Физо , зубчатое колесо | 315 000 000 [105] | +5,1% |
| 1862 | Леон Фуко , вращающееся зеркало | 298 000 000 ± 500 000 [105] | −0,60% |
| 1875 | Вернер Сименс | 260 000 000 [124] | |
| 1893 | Генрих Герц | 200 000 000 [125] | |
| 1907 | Роза и Дорси, константы ЭМ | 299 710 000 ± 30 000 [109] [110] | −280 частей на миллион |
| 1926 | Альберт А. Майкельсон , вращающееся зеркало | 299 796 000 ± 4000 [126] | +12 частей на миллион |
| 1950 | Эссен и Гордон-Смит , объемный резонатор | 299 792 500 ± 3000 [112] | +0,14 частей на миллион |
| 1958 | К.Д. Фрум, радиоинтерферометрия | 299 792 500 ± 100 [116] | +0,14 частей на миллион |
| 1972 | Эвенсон и др. , лазерная интерферометрия | 299 792 456 .2 ± 1.1 [118] | −0,006 частей на миллион |
| 1983 | 17-я ГКМВ, определение метра | 299 792 458 (точно) [93] | |
Ранняя история
Эмпедокл (ок. 490–430 до н. э.) был первым, кто предложил теорию света [127] и утверждал, что свет имеет конечную скорость. [128] Он утверждал, что свет — это нечто движущееся, и поэтому ему требуется некоторое время для перемещения. Аристотель утверждал, напротив, что «свет возникает из-за присутствия чего-то, но это не движение». [129] Евклид и Птолемей выдвинули эмиссионную теорию зрения Эмпедокла , согласно которой свет излучается из глаза, тем самым обеспечивая зрение. Основываясь на этой теории, Герон Александрийский утверждал, что скорость света должна быть бесконечной, потому что удаленные объекты, такие как звезды, появляются сразу после открытия глаз. [130]
Ранние исламские философы изначально соглашались с аристотелевским взглядом на то, что свет не имеет скорости перемещения. В 1021 году Альхазен (Ибн аль-Хайтам) опубликовал « Книгу оптики» , в которой он представил ряд аргументов, отвергающих эмиссионную теорию зрения в пользу ныне принятой теории интромиссии, в которой свет движется от объекта в глаз. [131] Это привело Альхазена к предположению, что свет должен иметь конечную скорость, [129] [132] [133] и что скорость света является переменной, уменьшаясь в более плотных телах. [133] [134] Он утверждал, что свет — это субстанциальная материя, распространение которой требует времени, даже если это скрыто от чувств. [135] Также в 11 веке Абу Райхан аль-Бируни согласился, что свет имеет конечную скорость, и заметил, что скорость света намного выше скорости звука. [136]
В XIII веке Роджер Бэкон утверждал, что скорость света в воздухе не бесконечна, используя философские аргументы, подкрепленные трудами Альхазена и Аристотеля. [137] [138] В 1270-х годах Витело рассматривал возможность распространения света с бесконечной скоростью в вакууме, но замедления в более плотных телах. [139]
В начале 17 века Иоганн Кеплер считал, что скорость света бесконечна, поскольку пустое пространство не представляет для нее никаких препятствий. Рене Декарт утверждал, что если бы скорость света была конечной, то Солнце, Земля и Луна были бы заметно не выровнены во время лунного затмения . Хотя этот аргумент несостоятелен, когда принимается во внимание аберрация света , последняя не была признана до следующего столетия. [140] Поскольку такое несовпадение не наблюдалось, Декарт пришел к выводу, что скорость света бесконечна. Декарт предположил, что если бы скорость света оказалась конечной, вся его философская система могла бы быть разрушена. [129] Несмотря на это, при выводе закона Снеллиуса Декарт предположил, что некий вид движения, связанный со светом, был быстрее в более плотных средах. [141] [142] Пьер де Ферма вывел закон Снеллиуса, используя противоположное предположение: чем плотнее среда, тем медленнее распространяется свет. Ферма также выступал в поддержку конечной скорости света. [143]
Первые попытки измерения
В 1629 году Исаак Бекман предложил эксперимент, в котором человек наблюдает вспышку пушки, отражающуюся от зеркала на расстоянии около одной мили (1,6 км). В 1638 году Галилео Галилей предложил эксперимент, с явным утверждением, что выполнил его несколькими годами ранее, для измерения скорости света путем наблюдения задержки между открытием фонаря и его восприятием на некотором расстоянии. Он не мог различить, было ли перемещение света мгновенным или нет, но пришел к выводу, что если это не так, оно, тем не менее, должно быть необычайно быстрым. [119] [120] В 1667 году Accademia del Cimento во Флоренции сообщила, что она провела эксперимент Галилея с фонарями, разделенными примерно одной милей, но никакой задержки не наблюдалось. [144] Фактическая задержка в этом эксперименте составила бы около 11 микросекунд .
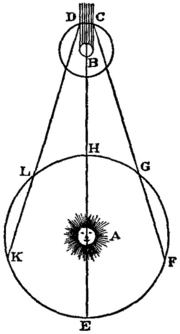
Первая количественная оценка скорости света была сделана в 1676 году Оле Рёмером. [94] [95] Из наблюдения, что периоды самой внутренней луны Юпитера Ио кажутся короче, когда Земля приближается к Юпитеру, чем когда удаляется от него, он пришел к выводу, что свет распространяется с конечной скоростью, и подсчитал, что свету требуется 22 минуты, чтобы пересечь диаметр орбиты Земли. Христиан Гюйгенс объединил эту оценку с оценкой диаметра орбиты Земли, чтобы получить оценку скорости света220 000 км/с , что на 27% ниже фактического значения. [123]
В своей книге 1704 года «Оптика » Исаак Ньютон сообщил о расчетах Рёмера относительно конечной скорости света и дал значение «семь или восемь минут» для времени, необходимого для прохождения света от Солнца до Земли (современное значение составляет 8 минут 19 секунд). [145] Ньютон задался вопросом, были ли тени затмения Рёмера цветными. Услышав, что это не так, он пришел к выводу, что разные цвета распространяются с одинаковой скоростью. В 1729 году Джеймс Брэдли открыл звездную аберрацию . [96] Из этого эффекта он определил, что свет должен двигаться в 10 210 раз быстрее, чем Земля по своей орбите (современное значение составляет 10 066 раз быстрее) или, что эквивалентно, что свету потребуется 8 минут 12 секунд, чтобы пройти путь от Солнца до Земли. [96]
Связи с электромагнетизмом
В XIX веке Ипполит Физо разработал метод определения скорости света на основе измерений времени пролета на Земле и сообщил значение315 000 км/с . [146] Его метод был усовершенствован Леоном Фуко , который получил значение298 000 км/с в 1862 году. [105] В 1856 году Вильгельм Эдуард Вебер и Рудольф Кольрауш измерили отношение электромагнитных и электростатических единиц заряда, 1/ √ ε 0 μ 0 , разряжая лейденскую банку , и обнаружили, что его численное значение было очень близко к скорости света, измеренной непосредственно Физо. В следующем году Густав Кирхгоф вычислил, что электрический сигнал в проводе без сопротивления распространяется по проводу с этой скоростью. [147]
В начале 1860-х годов Максвелл показал, что, согласно теории электромагнетизма, над которой он работал, электромагнитные волны распространяются в пустом пространстве [148] со скоростью, равной указанному выше отношению Вебера/Кольрауша, и, обратив внимание на численную близость этого значения к скорости света, измеренной Физо, он предположил, что свет на самом деле является электромагнитной волной. [149] Максвелл подкрепил свое утверждение собственным экспериментом, опубликованным в Philosophical Transactions 1868 года, который определил соотношение электростатических и электромагнитных единиц электричества. [150]
«Светоносный эфир»
Волновые свойства света были хорошо известны со времен Томаса Юнга . В 19 веке физики считали, что свет распространяется в среде, называемой эфиром (или эфиром). Но для электрической силы это больше похоже на силу тяготения в законе Ньютона. Передающая среда не требовалась. После того, как теория Максвелла объединила свет, электрические и магнитные волны, было высказано мнение, что и свет, и электромагнитные волны распространяются в одной и той же эфирной среде (или называемой светоносным эфиром ). [151]

В то время считалось, что пустое пространство заполнено фоновой средой, называемой светоносным эфиром , в которой существует электромагнитное поле. Некоторые физики считали, что этот эфир действует как предпочтительная система отсчета для распространения света, и поэтому должно быть возможно измерить движение Земли относительно этой среды, измеряя изотропию скорости света. Начиная с 1880-х годов было проведено несколько экспериментов, чтобы попытаться обнаружить это движение, самым известным из которых является эксперимент, проведенный Альбертом А. Майкельсоном и Эдвардом У. Морли в 1887 году. [152] [153] Было обнаружено, что обнаруженное движение всегда равно нулю (в пределах погрешности наблюдения). Современные эксперименты показывают, что двусторонняя скорость света изотропна ( одинакова во всех направлениях) с точностью до 6 нанометров в секунду. [154]
Из-за этого эксперимента Хендрик Лоренц предположил, что движение аппарата через эфир может заставить аппарат сжиматься по его длине в направлении движения, и он далее предположил, что переменная времени для движущихся систем также должна быть изменена соответствующим образом («местное время»), что привело к формулировке преобразования Лоренца . Основываясь на теории эфира Лоренца , Анри Пуанкаре (1900) показал, что это локальное время (в первом порядке по v / c ) указывается часами, движущимися в эфире, которые синхронизированы при предположении постоянной скорости света. В 1904 году он предположил, что скорость света может быть предельной скоростью в динамике, при условии, что все предположения теории Лоренца подтверждены. В 1905 году Пуанкаре привел теорию эфира Лоренца в полное наблюдательное согласие с принципом относительности . [155] [156]
Специальная теория относительности
В 1905 году Эйнштейн с самого начала постулировал, что скорость света в вакууме, измеренная неускоряющимся наблюдателем, не зависит от движения источника или наблюдателя. Используя это и принцип относительности в качестве основы, он вывел специальную теорию относительности , в которой скорость света в вакууме c фигурировала как фундаментальная константа, также появляясь в контекстах, не связанных со светом. Это сделало концепцию неподвижного эфира (которой все еще придерживались Лоренц и Пуанкаре) бесполезной и произвело революцию в концепциях пространства и времени. [157] [158]
Повышенная точностьси переопределение метра и секунды
Во второй половине 20-го века был достигнут значительный прогресс в повышении точности измерений скорости света, сначала с помощью методов резонанса полости, а затем с помощью методов лазерного интерферометра. Этому способствовали новые, более точные определения метра и секунды. В 1950 году Луи Эссен определил скорость как299 792 .5 ± 3.0 км/с , с использованием резонанса полости. [112] Это значение было принято 12-й Генеральной Ассамблеей Радионаучного Союза в 1957 году. В 1960 году метр был переопределен в терминах длины волны конкретной спектральной линии криптона-86 , а в 1967 году секунда была переопределена в терминах частоты сверхтонкого перехода основного состояния цезия-133 . [159]
В 1972 году группа исследователей из Национального бюро стандартов США в Боулдере, штат Колорадо, используя метод лазерного интерферометра и новые определения, определила скорость света в вакууме как c = 299 792 456 .2 ± 1.1 м/с . Это было в 100 раз менее неопределенным, чем ранее принятое значение. Оставшаяся неопределенность была в основном связана с определением метра. [Примечание 16] [118] Поскольку аналогичные эксперименты дали сопоставимые результаты для c , 15-я Генеральная конференция по мерам и весам в 1975 году рекомендовала использовать значение299 792 458 м/с — скорость света. [162]
Определено как явная константа
В 1983 году 17-е заседание Генеральной конференции по мерам и весам (CGPM) обнаружило, что длины волн из измерений частоты и заданное значение скорости света более воспроизводимы , чем предыдущий стандарт. Они сохранили определение секунды 1967 года, поэтому частота сверхтонкого цезия теперь будет определять и секунду, и метр. Для этого они переопределили метр как «длину пути, пройденного светом в вакууме за интервал времени 1/299 792 458 секунды». [93]
В результате этого определения значение скорости света в вакууме равно точно299 792 458 м/с [163] [164] и стала определенной константой в системе единиц СИ. [14] Улучшенные экспериментальные методы, которые до 1983 года измеряли скорость света, больше не влияют на известное значение скорости света в единицах СИ, но вместо этого позволяют более точно реализовать метр путем более точного измерения длины волны криптона-86 и других источников света. [165] [166]
В 2011 году CGPM заявила о своем намерении переопределить все семь основных единиц СИ, используя то, что она называет «формулировкой явной константы», где каждая «единица определяется косвенно путем явного указания точного значения общепризнанной фундаментальной константы», как это было сделано для скорости света. Она предложила новую, но полностью эквивалентную формулировку определения метра: «Метр, символ m, является единицей длины; его величина устанавливается путем фиксации численного значения скорости света в вакууме, которое должно быть точно равно299 792 458 , когда оно выражено в единицах СИ мс −1 ». [167] Это было одно из изменений, которое было включено в пересмотренную версию СИ 2019 года , также называемую Новой СИ . [168]
Смотрите также
Примечания
- ^ Точное значение: (299 792 458 ×86 400 /149 597 870 700 ) AU/день .
- ^ Точное значение: (999 992 651 π /10 246 429 500 ) шт/год .
- ^ Это точно, потому что согласно международному соглашению 1983 года метр определяется как длина пути, проходимого светом в вакууме за промежуток времени 1 ⁄299 792 458 секунд. Это конкретное значение было выбрано для того, чтобы дать более точное определение метра, которое по-прежнему максимально соответствовало определению, использовавшемуся ранее. См., например,веб-сайтNIST[2]или объяснениеПенроуза.[3]Секунда, в свою очередь, определяется как отрезок времени, занимаемый9 192 631 770 циклов излучения, испускаемого атомом цезия -133 при переходе между двумя указанными энергетическими состояниями . [2]
- ^ Скорость света в имперской системе равна точно
- 186 282 миль ,698 ярдов ,2 фута и 5+21/127 дюймов в секунду.
- ^ Точное значение 149 896 229/152 400 000 футы/нс ≈ 0,98 футы/нс .
- ^ Однако частота света может зависеть от движения источника относительно наблюдателя из-за эффекта Доплера .
- ^ См ., например, эксперимент Майкельсона–Морли и эксперимент Кеннеди–Торндайка .
- ^ Поскольку нейтрино имеют небольшую, но ненулевую массу, они движутся через пустое пространство немного медленнее света . Однако, поскольку они проходят через вещество гораздо легче, чем свет, теоретически возможны случаи, когда нейтринный сигнал от астрономического события может достичь Земли раньше, чем оптический сигнал, например, сверхновые . [25]
- ^ В то время как движущиеся объекты измеряются как более короткие вдоль линии относительного движения, они также рассматриваются как вращающиеся. Этот эффект, известный как вращение Террелла , обусловлен разным временем, которое требуется свету от разных частей объекта, чтобы достичь наблюдателя. [27] [28]
- ^ Было высказано предположение, что эффект Шарнхорста позволяет сигналам распространяться немного быстрее, чем c , но обоснованность этих расчетов была поставлена под сомнение, [41] и, по-видимому, особые условия, в которых этот эффект может возникнуть, не позволяют использовать его для нарушения причинности. [42]
- ^ Типичное значение показателя преломления оптического волокна составляет от 1,518 до 1,538. [78]
- ^ Астрономическая единица была определена как радиус невозмущенной круговой ньютоновской орбиты вокруг Солнца частицы, имеющей бесконечно малую массу, движущейся с угловой частотой 0,017 202 098 95 радиан ( приблизительно 1 ⁄365,256 898 оборота) в день.[100]
- ^ Тем не менее, при такой степени точности необходимо учитывать эффекты общей теории относительности при интерпретации длины. Метр считается единицей собственной длины , тогда как AU обычно используется как единица наблюдаемой длины в данной системе отсчета. Значения, приведенные здесь, следуют последнему соглашению и совместимы с TDB . [103]
- ^ Подробное обсуждение интерферометра и его использования для определения скорости света можно найти в работе Вогана (1989). [115]
- ^ По словам Галилея, фонари, которые он использовал, находились «на небольшом расстоянии, менее мили». Предполагая, что расстояние было не намного короче мили, и что «около тридцатой доли секунды — минимальный временной интервал, различимый невооруженным глазом», Бойер отмечает, что эксперимент Галилея в лучшем случае можно было бы назвать установлением нижнего предела скорости света около 60 миль в секунду. [120]
- ^ В период с 1960 по 1983 год метр определялся как «длина, равная1 650 763 .73 длины волны в вакууме излучения, соответствующего переходу между уровнями 2p 10 и 5d 5 атома криптона-86». [160] В 1970-х годах было обнаружено, что эта спектральная линия не является симметричной, что накладывает ограничение на точность, с которой определение может быть реализовано в экспериментах по интерферометрии. [161]
Ссылки
- ^ Ларсон, Рон; Хостетлер, Роберт П. (2007). Элементарная и средняя алгебра: комбинированный курс, издание для поддержки студентов (4-е иллюстрированное издание). Cengage Learning. стр. 197. ISBN 978-0-618-75354-3.
- ^ ab "Определения основных единиц СИ". physics.nist.gov . 29 мая 2019 г. Получено 8 февраля 2022 г.
- ^ Пенроуз, Р. (2004). Дорога к реальности: полное руководство по законам Вселенной . Винтажные книги. стр. 410–411. ISBN 978-0-679-77631-4...
наиболее точный стандарт для метра удобно
определяется
так , чтобы было точно Из них 299 792 458 — к расстоянию, которое проходит свет за стандартную секунду, что дает значение метра, которое очень точно соответствует недостаточно точному в настоящее время стандартному правилу метра в Париже.
- ^ Моисей Файнгольд (2008). Специальная теория относительности и как она работает (иллюстрированное издание). John Wiley & Sons. стр. 497. ISBN 978-3-527-40607-4.Выдержка из страницы 497.
- ^ Альберт Шэдоуиц (1988). Специальная теория относительности (пересмотренное издание). Courier Corporation. стр. 79. ISBN 978-0-486-65743-1.Выдержка из страницы 79.
- ^ Перес, Эшер ; Терно, Дэниел Р. (6 января 2004 г.). «Квантовая информация и теория относительности». Reviews of Modern Physics . 76 (1): 93–123. arXiv : quant-ph/0212023 . Bibcode : 2004RvMP...76...93P. doi : 10.1103/RevModPhys.76.93. ISSN 0034-6861. S2CID 7481797.
- ^ Гиббс, Филипп (1997). «Как измеряется скорость света?». FAQ по физике и теории относительности . Архивировано из оригинала 21 августа 2015 г.
- ^ аб Стачел, Джей-Джей (2002). Эйнштейн от «Б» до «Я» - Том 9 исследований Эйнштейна. Спрингер. п. 226. ИСБН 978-0-8176-4143-6.
- ^ См., например:
- Фейгенбаум, Митчелл Дж .; Мермин, Н. Дэвид (январь 1988 г.). "E = mc2". American Journal of Physics . 56 (1): 18–21. Bibcode : 1988AmJPh..56...18F. doi : 10.1119/1.15422. ISSN 0002-9505.
- Узан, Дж. П.; Леклерк, Б. (2008). Естественные законы Вселенной: понимание фундаментальных констант. Springer. стр. 43–44. ISBN 978-0-387-73454-5.
- ^ Гиббс, П. (2004) [1997]. "Почему c — символ скорости света?". Часто задаваемые вопросы по физике Usenet . Калифорнийский университет, Риверсайд . Архивировано из оригинала 25 марта 2010 г. Получено 16 ноября 2009 г.«Истоки использования буквы c для обозначения скорости света можно проследить до статьи Вебера и Кольрауша 1856 года [...] Вебер, по-видимому, подразумевал, что c означает «константа» в своем законе силы, но есть свидетельства того, что физики, такие как Лоренц и Эйнштейн, привыкли к общему соглашению, что c можно использовать как переменную для скорости. Такое использование можно проследить до классических латинских текстов, в которых c означало «celeritas», что означает «скорость».
- ^ Мендельсон, К. С. (2006). «История c ». Американский журнал физики . 74 (11): 995–997. Bibcode : 2006AmJPh..74..995M. doi : 10.1119/1.2238887. ISSN 0002-9505.
- ^ См., например:
- Лид, DR (2004). Справочник CRC по химии и физике. CRC Press . стр. 2–9. ISBN 978-0-8493-0485-9.
- Харрис, Дж. В. и др. (2002). Справочник по физике. Springer. стр. 499. ISBN 978-0-387-95269-7.
- Whitaker, JC (2005). Справочник по электронике. CRC Press. стр. 235. ISBN 978-0-8493-1889-4.
- Коэн, Э. Р. и др. (2007). Величины, единицы и символы в физической химии (3-е изд.). Королевское химическое общество . стр. 184. ISBN 978-0-85404-433-7.
- ^ Международное бюро мер и весов (2006), Международная система единиц (СИ) (PDF) (8-е изд.), стр. 112, ISBN 92-822-2213-6, заархивировано (PDF) из оригинала 4 июня 2021 г. , извлечено 16 декабря 2021 г.
- ^ ab См., например:
- Sydenham, PH (2003). «Измерение длины». В Boyes, W (ред.). Справочник по приборам (3-е изд.). Butterworth–Heinemann . стр. 56. ISBN 978-0-7506-7123-1.
... если скорость света определить как фиксированное число, то, в принципе, эталон времени будет служить эталоном длины ...
- "Значение CODATA: Скорость света в вакууме". Справочник NIST по константам, единицам и неопределенности . NIST . Получено 21 августа 2009 г.
- Йесперсен, Дж.; Фиц-Рэндольф, Дж.; Робб, Дж. (1999). От солнечных часов до атомных: понимание времени и частоты (переиздание Национального бюро стандартов 1977 г., 2-е изд.). Courier Dover . стр. 280. ISBN 978-0-486-40913-9.
- Sydenham, PH (2003). «Измерение длины». В Boyes, W (ред.). Справочник по приборам (3-е изд.). Butterworth–Heinemann . стр. 56. ISBN 978-0-7506-7123-1.
- ^ Мермин, Н. Дэвид (2005). Время пришло: понимание теории относительности Эйнштейна. Принстон: Princeton University Press. стр. 22. ISBN 0-691-12201-6. OCLC 57283944.
- ^ «Наносекунды, связанные с Грейс Хоппер». Национальный музей американской истории . Получено 1 марта 2022 г. Грейс
Мюррей Хоппер
(1906–1992), математик, ставшая военно-морским офицером и специалистом по информатике во время Второй мировой войны, начала распространять эти проволочные «наносекунды» в конце 1960-х годов, чтобы продемонстрировать, как проектирование более мелких компонентов позволит производить более быстрые компьютеры.
- ^ Lawrie, ID (2002). "Приложение C: Естественные единицы". A Unified Grand Tour of Theoretical Physics (2-е изд.). CRC Press. стр. 540. ISBN 978-0-7503-0604-1.
- ^ Hsu, L. (2006). «Приложение A: Системы единиц и развитие теорий относительности». A Wider View of Relativity: General Implications of Lorentz and Poincaré Invariance (2-е изд.). World Scientific . стр. 427–428. ISBN 978-981-256-651-5.
- ^ Эйнштейн, А. (1905). «Zur Elektrodynamic bewegter Körper». Annalen der Physik (Представленная рукопись) (на немецком языке). 17 (10): 890–921. Бибкод : 1905АнП...322..891Е. дои : 10.1002/andp.19053221004 .Перевод на английский язык: Perrett, W. Walker, J (ред.). "On the Electrodynamics of Moving Bodies". Fourmilab . Перевод Jeffery, G. B. Получено 27 ноября 2009 г.
- ^ ab Hsu, J.-P.; Zhang, YZ (2001). Лоренц-инвариантность и инвариантность Пуанкаре. Расширенная серия по теоретической физической науке. Том 8. World Scientific . стр. 543 и далее. ISBN 978-981-02-4721-8.
- ^ abc Zhang, YZ (1997). Специальная теория относительности и ее экспериментальные основы. Расширенная серия по теоретической физической науке. Том 4. World Scientific . С. 172–173. ISBN 978-981-02-2749-4. Получено 23 июля 2009 г.
- ^ d'Inverno, R. (1992). Введение в теорию относительности Эйнштейна. Oxford University Press. С. 19–20. ISBN 978-0-19-859686-8.
- ^ Шриранджан, Б. (2004). "Постулаты специальной теории относительности и их следствия". Специальная теория относительности . PHI Learning Pvt. Ltd. стр. 20 и далее. ISBN 978-81-203-1963-9.
- ^ ab Эллис, Джордж ФР ; Уильямс, Рут М. (2000). Плоское и искривленное пространство-время (2-е изд.). Оксфорд: Oxford University Press. стр. 12. ISBN 0-19-850657-0. OCLC 44694623.
- ^ Антониоли, Пьетро; Файнберг, Ричард Треш; Флеро, Фабрис; Фукуда, Ёсиюки; Фульджионе, Уолтер; Хабиг, Алек; Хайзе, Джарет; Макдональд, Артур Б.; Миллс, Коррин; Намба, Тошио; Робинсон, Лейф Дж. (2 сентября 2004 г.). "SNEWS: система раннего оповещения о сверхновых". New Journal of Physics . 6 : 114. arXiv : astro-ph/0406214 . Bibcode : 2004NJPh....6..114A. doi : 10.1088/1367-2630/6/1/114. ISSN 1367-2630. S2CID 119431247.
- ^ Робертс, Т.; Шлейф, С. (2007). Длугош, Дж. М. (ред.). «Какова экспериментальная основа специальной теории относительности?». Часто задаваемые вопросы по физике Usenet . Калифорнийский университет, Риверсайд . Архивировано из оригинала 15 октября 2009 г. Получено 27 ноября 2009 г.
- ^ Террелл, Дж. (1959). «Невидимость сокращения Лоренца». Physical Review . 116 (4): 1041–1045. Bibcode : 1959PhRv..116.1041T. doi : 10.1103/PhysRev.116.1041.
- ^ Пенроуз, Р. (1959). «Видимая форма релятивистски движущейся сферы». Труды Кембриджского философского общества . 55 (1): 137–139. Bibcode : 1959PCPS...55..137P. doi : 10.1017/S0305004100033776. S2CID 123023118.
- ^ Хартл, Дж. Б. (2003). Гравитация: Введение в общую теорию относительности Эйнштейна. Эддисон-Уэсли . С. 52–59. ISBN 978-981-02-2749-4.
- ^ Хартл, Дж. Б. (2003). Гравитация: Введение в общую теорию относительности Эйнштейна . Эддисон-Уэсли . стр. 332. ISBN 978-981-02-2749-4.
- ^ См., например:
- Эбботт, Б. П.; и др. (2017). «Гравитационные волны и гамма-лучи от слияния двойной нейтронной звезды: GW170817 и GRB 170817A». The Astrophysical Journal Letters . 848 (2): L13. arXiv : 1710.05834 . Bibcode : 2017ApJ...848L..13A. doi : 10.3847/2041-8213/aa920c .
- Корниш, Нил; Блас, Диего; Нардини, Джермано (18 октября 2017 г.). «Ограничение скорости гравитации с помощью наблюдений гравитационных волн». Physical Review Letters . 119 (16): 161102. arXiv : 1707.06101 . Bibcode :2017PhRvL.119p1102C. doi :10.1103/PhysRevLett.119.161102. PMID 29099221. S2CID 206300556.
- Лю, Сяошу; Хэ, Винсент Ф.; Микульски, Тимоти М.; Паленова, Дарья; Уильямс, Клэр Э.; Крейтон, Джолиен; Тассон, Джей Д. (7 июля 2020 г.). «Измерение скорости гравитационных волн из первого и второго наблюдательного запуска Advanced LIGO и Advanced Virgo». Physical Review D. 102 ( 2): 024028. arXiv : 2005.03121 . Bibcode : 2020PhRvD.102b4028L. doi : 10.1103/PhysRevD.102.024028. S2CID 220514677.
- ^ ab Gibbs, P. (1997) [1996]. Carlip, S. (ред.). "Is The Speed of Light Constant?". Usenet Physics FAQ . Калифорнийский университет, Риверсайд . Архивировано из оригинала 2 апреля 2010 г. Получено 26 ноября 2009 г.
- ^ Эллис, СКФ; Узан, Ж.-П. (2005). "«c» — это скорость света, не так ли?». American Journal of Physics . 73 (3): 240–227. arXiv : gr-qc/0305099 . Bibcode : 2005AmJPh..73..240E. doi : 10.1119/1.1819929. S2CID 119530637.
Возможность того, что фундаментальные константы могут меняться в ходе эволюции Вселенной, открывает исключительную возможность для изучения теорий более высоких измерений и, вероятно, связана с природой темной энергии, которая заставляет Вселенную ускоряться сегодня.
- ^ Мота, ДФ (2006). Вариации постоянной тонкой структуры в пространстве и времени (PhD). arXiv : astro-ph/0401631 . Bibcode :2004astro.ph..1631M.
- ^ Uzan, J.-P. (2003). "Фундаментальные константы и их вариации: наблюдательный статус и теоретические мотивы". Reviews of Modern Physics . 75 (2): 403. arXiv : hep-ph/0205340 . Bibcode :2003RvMP...75..403U. doi :10.1103/RevModPhys.75.403. S2CID 118684485.
- ^ Амелино-Камелия, Г. (2013). «Феноменология квантовой гравитации». Living Reviews in Relativity . 16 (1): 5. arXiv : 0806.0339 . Bibcode : 2013LRR....16....5A. doi : 10.12942/lrr-2013-5 . PMC 5255913. PMID 28179844.
- ^ Herrmann, S.; Senger, A.; Möhle, K.; Nagel, M.; Kovalchuk, EV; Peters, A. (2009). "Эксперимент с вращающейся оптической полостью, проверяющий инвариантность Лоренца на уровне 10−17 " . Physical Review D. 80 ( 100): 105011. arXiv : 1002.1284 . Bibcode : 2009PhRvD..80j5011H. doi : 10.1103/PhysRevD.80.105011. S2CID 118346408.
- ^ Ланг, К. Р. (1999). Астрофизические формулы (3-е изд.). Биркхойзер. стр. 152. ISBN 978-3-540-29692-8.
- ^ См., например:
- «Официально: машины времени не работают». Los Angeles Times . 25 июля 2011 г.
- «Профессора HKUST доказали, что одиночные фотоны не превышают скорость света». Гонконгский университет науки и технологий . 19 июля 2011 г.
- Shanchao Zhang; JF Chen; Chang Liu; MMT Loy; GKL Wong; Shengwang Du (16 июня 2011 г.). "Оптический предшественник одиночного фотона" (PDF) . Physical Review Letters . 106 (243602): 243602. Bibcode : 2011PhRvL.106x3602Z. doi : 10.1103/physrevlett.106.243602. PMID 21770570.
- ^ Фаулер, М. (март 2008 г.). «Заметки о специальной теории относительности» (PDF) . Университет Вирджинии. стр. 56. Получено 7 мая 2010 г.
- ^ См., например:
- Бен-Менахем, Шахар (ноябрь 1990 г.). «Причинность между проводящими пластинами». Physics Letters B. 250 ( 1–2): 133–138. Bibcode : 1990PhLB..250..133B. doi : 10.1016/0370-2693(90)91167-A. OSTI 1449261.
- Fearn, H. (10 ноября 2006 г.). «Дисперсионные соотношения и причинность: требует ли релятивистская причинность, чтобы n (ω) → 1 при ω → ∞ ?». Journal of Modern Optics . 53 (16–17): 2569–2581. Bibcode :2006JMOp...53.2569F. doi :10.1080/09500340600952085. ISSN 0950-0340. S2CID 119892992.
- Fearn, H. (май 2007). «Могут ли световые сигналы распространяться быстрее, чем c в нетривиальном вакууме в плоском пространстве-времени? Релятивистская причинность II». Laser Physics . 17 (5): 695–699. arXiv : 0706.0553 . Bibcode :2007LaPhy..17..695F. doi :10.1134/S1054660X07050155. ISSN 1054-660X. S2CID 61962.
- ^ Либерати, С.; Сонего, С.; Виссер, М. (2002). «Сигналы быстрее с , специальная теория относительности и причинность». Annals of Physics . 298 (1): 167–185. arXiv : gr-qc/0107091 . Bibcode : 2002AnPhy.298..167L. doi : 10.1006/aphy.2002.6233. S2CID 48166.
- ^ Тейлор, Э. Ф.; Уилер , Дж. А. (1992). Физика пространства-времени. WH Freeman. стр. 74–75. ISBN 978-0-7167-2327-1.
- ^ Толмен, RC (2009) [1917]. «Скорости, превышающие скорость света». Теория относительности движения (Переиздание). BiblioLife . стр. 54. ISBN 978-1-103-17233-7.
- ^ Хехт, Э. (1987). Оптика (2-е изд.). Эддисон-Уэсли. стр. 62. ISBN 978-0-201-11609-0.
- ^ Куимби, Р. С. (2006). Фотоника и лазеры: введение. John Wiley and Sons. стр. 9. ISBN 978-0-471-71974-8.
- ^ Вертхайм, М. (20 июня 2007 г.). «Тень уходит». The New York Times . Получено 21 августа 2009 г.
- ^ abc Gibbs, P. (1997). "Возможны ли сверхсветовые путешествия или коммуникации?". Usenet Physics FAQ . Калифорнийский университет, Риверсайд . Архивировано из оригинала 10 марта 2010 г. Получено 20 августа 2008 г.
- ^ См., например:
- Sakurai, JJ (1994). Tuan, SF (ред.). Modern Quantum Mechanics (пересмотренное издание). Addison-Wesley. стр. 231–232. ISBN 978-0-201-53929-5.
- Перес, Эшер (1993). Квантовая теория: концепции и методы . Kluwer . стр. 170. ISBN 0-7923-2549-4. OCLC 28854083.
- Кейвс, Карлтон М. (2015). «Квантовая информатика: больше не появляется». OSA Century of Optics . Optica . С. 320–326. arXiv : 1302.1864 . ISBN 978-1-943-58004-0.
[Б]ыло естественно мечтать о том, что квантовые корреляции могут быть использованы для сверхсветовой связи, но эта догадка была быстро развеяна, и стрельба установила принцип, согласно которому квантовые состояния не могут быть скопированы.
- ^ Муга, JG; Маято, РС; Эгускиса, Иллинойс, ред. (2007). Время в квантовой механике. Спрингер. п. 48. ИСБН 978-3-540-73472-7.
- ^ Эрнандес-Фигероа, HE; Замбони-Рачед, М.; Реками, Э. (2007). Локализованные волны. Уайли Интерсайенс . п. 26. ISBN 978-0-470-10885-7.
- ^ Wynne, K. (2002). "Причинность и природа информации" (PDF) . Optics Communications . 209 (1–3): 84–100. Bibcode :2002OptCo.209...85W. doi :10.1016/S0030-4018(02)01638-3. Архивировано из оригинала (PDF) 25 марта 2009 г.
- ^ Риз, М. (1966). "Появление релятивистски расширяющихся радиоисточников". Nature . 211 (5048): 468. Bibcode :1966Natur.211..468R. doi :10.1038/211468a0. S2CID 41065207.
- ^ Чейз, IP "Кажущаяся сверхсветовая скорость галактик". Часто задаваемые вопросы по физике Usenet . Калифорнийский университет, Риверсайд . Получено 26 ноября 2009 г.
- ↑ Райх, Эжени Сэмюэл (2 апреля 2012 г.). «Руководители проекта нейтрино, находящиеся в состоянии боевой готовности, уходят в отставку». Nature News . doi :10.1038/nature.2012.10371. S2CID 211730430 . Получено 11 февраля 2022 г. .
- ^ OPERA Collaboration (12 июля 2012 г.). «Измерение скорости нейтрино с помощью детектора OPERA в пучке CNGS». Журнал физики высоких энергий . 2012 (10): 93. arXiv : 1109.4897 . Bibcode : 2012JHEP...10..093A. doi : 10.1007/JHEP10(2012)093. S2CID 17652398.
- ^ Харрисон, Э. Р. (2003). Маски Вселенной. Cambridge University Press. стр. 206. ISBN 978-0-521-77351-5.
- ^ Панофски, В. К. Х.; Филлипс, М. (1962). Классическое электричество и магнетизм . Эддисон-Уэсли. стр. 182. ISBN 978-0-201-05702-7.
- ^ См., например:
- Шефер, Б. Э. (1999). «Жесткие ограничения на изменения скорости света в зависимости от частоты». Physical Review Letters . 82 (25): 4964–4966. arXiv : astro-ph/9810479 . Bibcode : 1999PhRvL..82.4964S. doi : 10.1103/PhysRevLett.82.4964. S2CID 119339066.
- Эллис, Дж.; Мавроматос, Н. Э .; Нанопулос, Д. В.; Сахаров, А. С. (2003). «Квантово-гравитационный анализ гамма-всплесков с использованием вейвлетов». Астрономия и астрофизика . 402 (2): 409–424. arXiv : astro-ph/0210124 . Bibcode : 2003A&A...402..409E. doi : 10.1051/0004-6361:20030263. S2CID 15388873.
- Фюллекруг, М. (2004). «Исследование скорости света с помощью радиоволн на крайне низких частотах». Physical Review Letters . 93 (4): 043901. Bibcode : 2004PhRvL..93d3901F. doi : 10.1103/PhysRevLett.93.043901. PMID 15323762.
- Bartlett, DJ; Desmond, H.; Ferreira, PG; Jasche, J. (17 ноября 2021 г.). «Ограничения на квантовую гравитацию и массу фотона из гамма-всплесков». Physical Review D. 104 ( 10): 103516. arXiv : 2109.07850 . Bibcode : 2021PhRvD.104j3516B. doi : 10.1103/PhysRevD.104.103516. ISSN 2470-0010. S2CID 237532210.
- ^ ab Adelberger, E.; Dvali, G.; Gruzinov, A. (2007). "Связанная масса фотона, разрушенная вихрями". Physical Review Letters . 98 (1): 010402. arXiv : hep-ph/0306245 . Bibcode : 2007PhRvL..98a0402A. doi : 10.1103/PhysRevLett.98.010402. PMID 17358459. S2CID 31249827.
- ^ Сидхарт, Б. Г. (2008). Термодинамическая Вселенная. World Scientific . стр. 134. ISBN 978-981-281-234-6.
- ^ Амелино-Камелия, Г. (2009). «Астрофизика: взрыв поддержки теории относительности». Nature . 462 (7271): 291–292. Bibcode :2009Natur.462..291A. doi : 10.1038/462291a . PMID 19924200. S2CID 205051022.
- ^ abc Milonni, Peter W. (2004). Быстрый свет, медленный свет и левосторонний свет. CRC Press. стр. 25 и далее . ISBN 978-0-7503-0926-4.
- ^ де Подеста, М. (2002). Понимание свойств материи. CRC Press. стр. 131. ISBN 978-0-415-25788-6.
- ^ "Оптические константы H2O, D2O (вода, тяжелая вода, лед)". Refractiveindex.info . Михаил Полянский . Получено 7 ноября 2017 г. .
- ^ "Оптические константы натриево-кальциевого стекла". Refractiveindex.info . Михаил Полянский . Получено 7 ноября 2017 г. .
- ^ "Оптические константы C (углерод, алмаз, графит)". Refractiveindex.info . Михаил Полянский . Получено 7 ноября 2017 г. .
- ^ Кроми, Уильям Дж. (24 января 2001 г.). «Исследователи теперь могут остановить и перезапустить свет». Harvard University Gazette . Архивировано из оригинала 28 октября 2011 г. Получено 8 ноября 2011 г.
- ^ Milonni, PW (2004). Быстрый свет, медленный свет и левосторонний свет. CRC Press. стр. 25. ISBN 978-0-7503-0926-4.
- ^ Толл, Дж. С. (1956). «Причинность и дисперсионное отношение: логические основы». Physical Review . 104 (6): 1760–1770. Bibcode : 1956PhRv..104.1760T. doi : 10.1103/PhysRev.104.1760.
- ^ Вольф, Эмиль (2001). «Аналитичность, причинность и дисперсионные отношения». Избранные труды Эмиля Вольфа: с комментариями. River Edge, NJ: World Scientific. стр. 577–584. ISBN 978-981-281-187-5. OCLC 261134839.
- ^ Libbrecht, KG; Libbrecht, MW (декабрь 2006 г.). «Интерферометрическое измерение резонансного поглощения и показателя преломления в газе рубидия» (PDF) . American Journal of Physics . 74 (12): 1055–1060. Bibcode :2006AmJPh..74.1055L. doi :10.1119/1.2335476. ISSN 0002-9505.
- ^ См., например:
- Hau, LV ; Harris, SE ; Dutton, Z. ; Behroozi, CH (1999). «Уменьшение скорости света до 17 метров в секунду в ультрахолодном атомарном газе» (PDF) . Nature . 397 (6720): 594–598. Bibcode :1999Natur.397..594V. doi :10.1038/17561. S2CID 4423307.
- Liu, C.; Dutton, Z .; Behroozi, CH; Hau, LV (2001). «Наблюдение за когерентным хранением оптической информации в атомной среде с использованием остановленных световых импульсов» (PDF) . Nature . 409 (6819): 490–493. Bibcode :2001Natur.409..490L. doi :10.1038/35054017. PMID 11206540. S2CID 1894748.
- Bajcsy, M.; Zibrov, AS; Lukin, MD (2003). "Стационарные импульсы света в атомной среде". Nature . 426 (6967): 638–641. arXiv : quant-ph/0311092 . Bibcode :2003Natur.426..638B. doi :10.1038/nature02176. PMID 14668857. S2CID 4320280.
- Дюме, Б. (2003). «Включение и выключение света». Physics World . Institute of Physics. Архивировано из оригинала 5 декабря 2008 г. Получено 8 декабря 2008 г.
- ^ См., например:
- Chiao, RY (1993). "Сверхсветовое (но причинное) распространение волновых пакетов в прозрачных средах с инвертированными атомными заселенностями". Physical Review A. 48 ( 1): R34–R37. Bibcode : 1993PhRvA..48...34C. doi : 10.1103/PhysRevA.48.R34. PMID 9909684.
- Ван, Л. Дж.; Кузмич, А.; Догариу, А. (2000). «Распространение сверхсветового света с усилением». Nature . 406 (6793): 277–279. doi :10.1038/35018520. PMID 10917523. S2CID 4358601.
- Уайтхаус, Д. (19 июля 2000 г.). «Луч разбивает световой барьер». BBC News . Получено 9 февраля 2022 г. .
- Гбур, Грег (26 февраля 2008 г.). «Свет, нарушающий собственный предел скорости: как работают «сверхсветовые» махинации» . Получено 9 февраля 2022 г.
- ^ Черенков, Павел А. (1934). «Видимое свечение чистых жидкостей под действием γ-излучения». Доклады Академии наук СССР . 2 : 451.Печатается: Черенков П.А. (1967). «Видимое свечение чистых жидкостей под действием γ-излучения». Усп. Физ. Наук . 93 (10): 385. doi :10.3367/ufnr.0093.196710n.0385.и у А. Н. Горбунова; Е. П. Черенкова, ред. (1999). Павел Алексеевич Черенков : Человек и открытие . Москва: Наука. стр. 149–153.
- ^ Пархами, Б. (1999). Введение в параллельную обработку: алгоритмы и архитектуры. Plenum Press . стр. 5. ISBN 978-0-306-45970-2.
- ^ Imbs, D.; Raynal, Michel (2009). Малышкин, В. (ред.). Программные транзакционные памяти: подход к многоядерному программированию. 10-я международная конференция PaCT 2009, Новосибирск, Россия, 31 августа – 4 сентября 2009 г. Springer. стр. 26. ISBN 978-3-642-03274-5.
- ^ Midwinter, JE (1991). Оптические волокна для передачи (2-е изд.). Krieger Publishing Company. ISBN 978-0-89464-595-2.
- ^ "Теоретический и реальный предел скорости Ping". Pingdom . Июнь 2007. Архивировано из оригинала 2 сентября 2010. Получено 5 мая 2010 .
- ^ Бьюкенен, Марк (11 февраля 2015 г.). «Физика в финансах: торговля со скоростью света». Nature . 518 (7538): 161–163. Bibcode :2015Natur.518..161B. doi : 10.1038/518161a . PMID 25673397.
- ^ "Время — деньги, когда дело касается микроволновых печей" . Financial Times . 10 мая 2013 г. Архивировано из оригинала 10 декабря 2022 г. Получено 25 апреля 2014 г.
- ^ "День 4: Лунные орбиты 7, 8 и 9". Журнал полета Аполлона 8. НАСА. Архивировано из оригинала 4 января 2011 года . Получено 16 декабря 2010 года .
- ^ Ормстон, Томас (8 мая 2012 г.). «Временная задержка между Марсом и Землей – Mars Express». Миссия ЕКА на Красную планету MARS EXPRESS . Получено 16 июля 2024 г.
- ^ Паризи, Меган; Панонтин, Тина; Ву, Шу-Чие; Мактиг, Кейтлин; Вера, Алонсо (2023). «Влияние задержки связи на пилотируемые космические миссии». Аэрокосмические системы, ориентированные на человека, и приложения для обеспечения устойчивости . 98. Открытый доступ AHFE. doi :10.54941/ahfe1003920. ISBN 978-1-958651-74-2.
- ^ ab "Хаббл достигает "неоткрытой страны" первобытных галактик" (пресс-релиз). Научный институт космического телескопа . 5 января 2010 г.
- ^ "The Hubble Ultra Deep Field Lithograph" (PDF) . NASA . Получено 4 февраля 2010 г.
- ^ Мак, Кэти (2021). Конец всего (астрофизически говоря). Лондон: Penguin Books. стр. 18–19. ISBN 978-0-141-98958-7. OCLC 1180972461.
- ^ "МАС и астрономические единицы". Международный астрономический союз . Получено 11 октября 2010 г.
- ^ Дальнейшее обсуждение можно найти в разделе «StarChild Question of the Month for March 2000». StarChild . NASA. 2000 . Получено 22 августа 2009 .
- ^ Дики, Дж. О. и др. (июль 1994 г.). «Лазерная локация Луны: продолжающееся наследие программы «Аполлон»» (PDF) . Science . 265 (5171): 482–490. Bibcode :1994Sci...265..482D. doi :10.1126/science.265.5171.482. PMID 17781305. S2CID 10157934.
- ↑ Standish, EM (февраль 1982 г.). «Планетные эфемериды JPL». Celestial Mechanics . 26 (2): 181–186. Bibcode : 1982CeMec..26..181S. doi : 10.1007/BF01230883. S2CID 121966516.
- ^ Бернер, Дж. Б.; Брайант, С. Х.; Кинман, П. В. (ноябрь 2007 г.). «Измерение дальности, применяемое в сети дальней космической связи» (PDF) . Труды IEEE . 95 (11): 2202–2214. doi :10.1109/JPROC.2007.905128. S2CID 12149700.
- ^ abc "Резолюция 1 17-й ГКМВ". BIPM. 1983. Получено 23 августа 2009 .
- ^ abc Cohen, IB (1940). «Рёмер и первое определение скорости света (1676)». Isis . 31 (2): 327–379. doi :10.1086/347594. hdl : 2027/uc1.b4375710 . S2CID 145428377.
- ^ abc «Демонстрация движения света, найденная г-ном Рёмером из Королевской академии наук» [Демонстрация движения света, найденная г-ном Ремером из Королевской академии наук] (PDF) . Journal des sçavans (на французском языке): 233–236. 1676.
Переведено в «Демонстрация, касающаяся движения света, сообщенная из Парижа в Journal des Sçavans, и здесь переведено на английский язык». Philosophical Transactions of the Royal Society . 12 (136): 893–895. 1677. Bibcode :1677RSPT...12..893.. doi : 10.1098/rstl.1677.0024 .
Воспроизведено в Hutton, C.; Shaw, G.; Pearson, R., ред. (1809). «О движении света» М. Ромера. Философские труды Лондонского королевского общества с момента их основания в 1665 году, в 1800 году: сокращенное издание . Т. II. С 1673 по 1682 год. Лондон: C. & R. Baldwin. С. 397–398.
Отчет, опубликованный в Journal des sçavans, был основан на докладе, который Рёмер зачитал Французской академии наук в ноябре 1676 года (Коэн, 1940, стр. 346). - ^ abcd Брэдли, Дж. (1729). «Отчет о новом открытом движении неподвижных звезд». Philosophical Transactions . 35 : 637–660.
- ^ Даффетт-Смит, П. (1988). Практическая астрономия с вашим калькулятором . Cambridge University Press. стр. 62. ISBN 978-0-521-35699-2.Выдержка из страницы 62.
- ^ ab "Резолюция B2 о новом определении астрономической единицы длины" (PDF) . Международный астрономический союз. 2012.
- ^ "Дополнение 2014: Обновления к 8-му изданию (2006) брошюры СИ" (PDF) . Международная система единиц . Международное бюро мер и весов: 14. 2014.
- ^ Международное бюро мер и весов (2006), Международная система единиц (СИ) (PDF) (8-е изд.), стр. 126, ISBN 92-822-2213-6, заархивировано (PDF) из оригинала 4 июня 2021 г. , извлечено 16 декабря 2021 г.
- ^ Брамфилд, Джефф (14 сентября 2012 г.). «Астрономическая единица фиксируется». Nature . doi :10.1038/nature.2012.11416. ISSN 1476-4687. S2CID 123424704.
- ^ Смотрите следующее:
- Pitjeva, EV; Standish, EM (2009). «Предложения по массам трех крупнейших астероидов, отношению масс Луны и Земли и астрономической единице». Небесная механика и динамическая астрономия . 103 (4): 365–372. Bibcode :2009CeMDA.103..365P. doi :10.1007/s10569-009-9203-8. S2CID 121374703.
- "Астродинамические константы". Динамика Солнечной системы . Лаборатория реактивного движения . Получено 10 февраля 2022 г.
- ^ ab Рабочая группа IAU по числовым стандартам для фундаментальной астрономии. "IAU WG on NSFA Current Best Estimates". Военно-морская обсерватория США . Архивировано из оригинала 8 декабря 2009 года . Получено 25 сентября 2009 года .
- ^ "NPL's Beginner's Guide to Length". UK National Physical Laboratory . Архивировано из оригинала 31 августа 2010 года . Получено 28 октября 2009 года .
- ^ abcde Гиббс, П. (1997). "Как измеряется скорость света?". Часто задаваемые вопросы по физике Usenet . Калифорнийский университет, Риверсайд. Архивировано из оригинала 21 августа 2015 г. Получено 13 января 2010 г.
- ^ Фаулер, М. "Скорость света". Университет Вирджинии . Получено 21 апреля 2010 г.
- ^ Хьюз, Стефан (2012). Ловцы света: забытые жизни мужчин и женщин, которые первыми сфотографировали небеса. ArtDeCiel Publishing. стр. 210. ISBN 978-1-62050-961-6.
- ^ См., например:
- Кук, Дж.; Мартин, М.; Маккартни, Х.; Вильф, Б. (1968). «Прямое определение скорости света как общий физический лабораторный эксперимент». American Journal of Physics . 36 (9): 847. Bibcode : 1968AmJPh..36..847C. doi : 10.1119/1.1975166.
- Аоки, К.; Мицуи, Т. (2008). «Небольшой настольный эксперимент для прямого измерения скорости света». American Journal of Physics . 76 (9): 812–815. arXiv : 0705.3996 . Bibcode : 2008AmJPh..76..812A. doi : 10.1119/1.2919743. S2CID 117454437.
- Джеймс, МБ; Ормонд, РБ; Сташ, А.Дж. (1999). «Измерение скорости света для мириадов». Американский журнал физики . 67 (8): 681–714. Bibcode : 1999AmJPh..67..681J. doi : 10.1119/1.19352.
- ^ abcde Эссен, Л.; Гордон-Смит, А.С. (1948). «Скорость распространения электромагнитных волн, полученная из резонансных частот цилиндрического резонатора». Труды Лондонского королевского общества A . 194 (1038): 348–361. Bibcode :1948RSPSA.194..348E. doi : 10.1098/rspa.1948.0085 . JSTOR 98293.
- ^ ab Rosa, EB ; Dorsey, NE (1907). "Новое определение отношения электромагнитной к электростатической единице электричества". Бюллетень Бюро стандартов . 3 (6): 433. doi : 10.6028/bulletin.070 .
- ^ Эссен, Л. (1947). «Скорость электромагнитных волн». Nature . 159 (4044): 611–612. Bibcode : 1947Natur.159..611E. doi : 10.1038/159611a0. S2CID 4101717.
- ^ abc Эссен, Л. (1950). «Скорость распространения электромагнитных волн, полученная из резонансных частот цилиндрического резонатора». Труды Лондонского королевского общества A. 204 ( 1077): 260–277. Bibcode : 1950RSPSA.204..260E. doi : 10.1098/rspa.1950.0172. JSTOR 98433. S2CID 121261770.
- ^ Stauffer, RH (апрель 1997). "Finding the Speed of Light with Marshmallows". The Physics Teacher . 35 (4): 231. Bibcode : 1997PhTea..35..231S. doi : 10.1119/1.2344657 . Получено 15 февраля 2010 .
- ^ "BBC Look East at the speed of light". Сайт BBC Norfolk . Получено 15 февраля 2010 г.
- ^ Vaughan, JM (1989). Интерферометр Фабри-Перо. CRC Press. стр. 47, 384–391. ISBN 978-0-85274-138-2.
- ^ ab Froome, KD (1958). "Новое определение скорости электромагнитных волн в свободном пространстве". Труды Лондонского королевского общества. Серия A, Математические и физические науки . 247 (1248): 109–122. Bibcode :1958RSPSA.247..109F. doi :10.1098/rspa.1958.0172. JSTOR 100591. S2CID 121444888.
- ^ abc Салливан, ДБ (2001). «Скорость света по прямым измерениям частоты и длины волны». В Лиде, Д.Р. (ред.). Столетие совершенства в измерениях, стандартах и технологиях (PDF) . CRC Press. стр. 191–193. ISBN 978-0-8493-1247-2. Архивировано из оригинала (PDF) 13 августа 2009 года.
- ^ abc Evenson, KM; et al. (1972). "Скорость света по прямым измерениям частоты и длины волны стабилизированного метаном лазера". Physical Review Letters . 29 (19): 1346–1349. Bibcode : 1972PhRvL..29.1346E. doi : 10.1103/PhysRevLett.29.1346. S2CID 120300510.
- ^ ab Галилей, Г. (1954) [1638]. Диалоги о двух новых науках. Crew, H.; de Salvio A. (перевод). Dover Publications . стр. 43. ISBN 978-0-486-60099-4. Архивировано из оригинала 30 января 2019 . Получено 29 января 2019 .
- ^ abc Boyer, CB (1941). «Ранние оценки скорости света». Isis . 33 (1): 24. doi :10.1086/358523. S2CID 145400212.
- ^ ab Foschi, Renato; Leone, Matteo (2009), «Галилей, измерение скорости света и времени реакции», Perception , 38 (8): 1251–1259, doi : 10.1068/p6263, hdl : 2318/132957 , PMID 19817156, S2CID 11747908
- ^ Магалотти, Лоренцо (2001) [1667], Saggi di Naturali Esperienze fatte nell' Accademia del Cimento (цифровое, онлайн-издание), Флоренция: Istituto e Museo di Storia delle Scienze, стр. 265–266 , получено 25 сентября 2015 г.
- ^ аб Гюйгенс, К. (1690). Traitée de la Lumière (на французском языке). Пьер ван дер Аа. стр. 8–9.
- ^ Бухвальд, Джед; Йенг, Чен-Панг; Стимеров, Ноа; Бартон, Дженифер; Харрингтон, Куинн (1 марта 2021 г.). «Что Генрих Герц открыл об электрических волнах в 1887–1888 годах». Архив для History of Exact Sciences . 75 (2): 125–171. doi :10.1007/s00407-020-00260-1. ISSN 1432-0657. S2CID 253895826.
- ^ Герц, Генрих (1893). Электрические волны . Лондон: Macmillan and Co.
- ^ Майкельсон, АА (1927). «Измерение скорости света между горой Вильсон и горой Сан-Антонио». The Astrophysical Journal . 65 : 1. Bibcode : 1927ApJ....65....1M. doi : 10.1086/143021.
- ^ Вайнер, Джон; Нунес, Фредерико (2013). Взаимодействие света и материи: физика и инженерия в наномасштабе (иллюстрированное издание). OUP Oxford. стр. 1. ISBN 978-0-19-856766-0.Выдержка из страницы 1.
- ^ Сартон, Г. (1993). Древняя наука сквозь золотой век Греции. Courier Dover . стр. 248. ISBN 978-0-486-27495-9.
- ^ abc MacKay, RH; Oldford, RW (2000). «Научный метод, статистический метод и скорость света». Статистическая наука . 15 (3): 254–278. doi : 10.1214/ss/1009212817 .(нажмите «Историческая справка» в содержании)
- ^ Ахмед, Шериф Сайед (2014). Электронная микроволновая визуализация с помощью плоских мультистатических решеток. Logos Verlag Berlin. стр. 1. ISBN 978-3-8325-3621-3.Выдержка из страницы 1
- ^ Гросс, К. Г. (1999). «Огонь, исходящий из глаза». Neuroscientist . 5 : 58–64. doi :10.1177/107385849900500108. S2CID 84148912.
- ^ Хамарнех, С. (1972). «Обзор: Хаким Мохаммед Саид, Ибн аль-Хайтам ». Isis . 63 (1): 119. doi :10.1086/350861.
- ^ ab Lester, PM (2005). Визуальная коммуникация: изображения с сообщениями . Thomson Wadsworth . стр. 10–11. ISBN 978-0-534-63720-0.
- ^ О'Коннор, Джей-Джей ; Робертсон, EF «Абу Али аль-Хасан ибн аль-Хайсам». MacTutor Архив истории математики . Университет Сент-Эндрюс . Проверено 12 января 2010 г.
- ^ Lauginie, P. (2004). Измерение скорости света: почему? Скорость чего? (PDF) . Пятая международная конференция по истории науки в научном образовании. Кестхей, Венгрия. стр. 75–84. Архивировано из оригинала (PDF) 4 июля 2015 г. . Получено 12 августа 2017 г. .
- ^ О'Коннор, Джей-Джей; Робертсон, Э.Ф. «Абу хан Мухаммад ибн Ахмад аль-Бируни». MacTutor Архив истории математики . Университет Сент-Эндрюс . Проверено 12 января 2010 г.
- ^ Линдберг, Д.К. (1996). Роджер Бэкон и истоки «Перспективы» в Средние века: критическое издание и английский перевод «Перспективы» Бэкона, с введением и примечаниями. Oxford University Press. стр. 143. ISBN 978-0-19-823992-5.
- ^ Линдберг, Д.К. (1974). "Синтез конца тринадцатого века в оптике". В Эдварде Гранте (ред.). Источниковая книга по средневековой науке . Издательство Гарвардского университета. стр. 396. ISBN 978-0-674-82360-0.
- ^ Маршалл, П. (1981). «Николь Орем о природе, отражении и скорости света». Isis . 72 (3): 357–374 [367–374]. doi :10.1086/352787. S2CID 144035661.
- ^ Сакеллариадис, Спирос (1982). «Экспериментальное доказательство Декарта бесконечной скорости света и ответ Гюйгенса». Архив истории точных наук . 26 (1): 1–12. doi :10.1007/BF00348308. ISSN 0003-9519. JSTOR 41133639. S2CID 118187860.
- ^ Каджори, Флориан (1922). История физики в ее элементарных разделах: включая эволюцию физических лабораторий. Macmillan. стр. 76.
- ^ Смит, А. Марк (1987). «Теория света и преломления Декарта: рассуждение о методе». Труды Американского философского общества . 77 (3): i–92. doi :10.2307/1006537. ISSN 0065-9746. JSTOR 1006537.
- ^ Бойер, Карл Бенджамин (1959). Радуга: от мифа к математике . Томас Йоселофф. стр. 205–206. OCLC 763848561.
- ^ Foschi, Renato; Leone, Matteo (август 2009 г.). «Галилей, измерение скорости света и времени реакции». Perception . 38 (8): 1251–1259. doi :10.1068/p6263. hdl : 2318/132957 . ISSN 0301-0066. PMID 19817156. S2CID 11747908.
- ↑ Ньютон, И. (1704). «Prop. XI». Оптика.Текст Предложения XI идентичен в первом (1704) и втором (1719) изданиях.
- ^ Гварниери, М. (2015). «Два тысячелетия света: долгий путь к волнам Максвелла». Журнал промышленной электроники IEEE . 9 (2): 54–56, 60. doi :10.1109/MIE.2015.2421754. S2CID 20759821.
- ^ Кирхгоф, Г. (1857). «Über die Bewegung der Elektricität». Энн. Физ. 178 (12): 529–244. Бибкод : 1857АнП...178..529К. дои : 10.1002/andp.18571781203.
- ^ См., например:
- Джордано, Николас Дж. (2009). Колледжская физика: рассуждения и отношения. Cengage Learning. стр. 787. ISBN 978-0-534-42471-8.Выдержка из страницы 787
- Бергманн, Питер Гэбриел (1992). Загадка гравитации. Courier Dover Publications. стр. 17. ISBN 978-0-486-27378-5.Выдержка из страницы 17
- Баис, Сандер (2005). Уравнения: иконы знаний . Издательство Гарвардского университета. стр. 40. ISBN 978-0-674-01967-6.Выдержка из страницы 40
- ^ O'Connor, JJ; Robertson, EF (ноябрь 1997 г.). "Джеймс Клерк Максвелл". Школа математики и статистики, Университет Сент-Эндрюс . Архивировано из оригинала 28 января 2011 г. Получено 13 октября 2010 г.
- ^ Кэмпбелл, Льюис; Гарнетт, Уильям; Раутио, Джеймс С. «Жизнь Джеймса Клерка Максвелла», стр. 544, ISBN 978-1-77375-139-9 .
- ↑ Уотсон, EC (1 сентября 1957 г.). «О связях между светом и электричеством». American Journal of Physics . 25 (6): 335–343. Bibcode : 1957AmJPh..25..335W. doi : 10.1119/1.1934460. ISSN 0002-9505.
- ^ Консоли, Маурицио; Плучино, Алессандро (2018). Эксперименты Майкельсона-Морли: загадка для физики и истории науки. World Scientific. стр. 118–119. ISBN 978-9-813-27818-9. Получено 4 мая 2020 г. .
- ^ Майкельсон, AA; Морли, EW (1887). «Об относительном движении Земли и светоносного эфира». American Journal of Science . 34 (203): 333–345. doi :10.1366/0003702874447824. S2CID 98374065.
- ^ Френч, AP (1983). Специальная теория относительности . Ван Ностранд Рейнхольд. С. 51–57. ISBN 978-0-442-30782-0.
- ^ Дарригол, О. (2000). Электродинамика от Ампера до Эйнштейна . Clarendon Press. ISBN 978-0-19-850594-5.
- ^ Галисон, П. (2003). Часы Эйнштейна, Карты Пуанкаре: Империи времени . WW Norton. ISBN 978-0-393-32604-8.
- ^ Миллер, AI (1981). Специальная теория относительности Альберта Эйнштейна. Возникновение (1905) и ранняя интерпретация (1905–1911) . Эддисон–Уэсли. ISBN 978-0-201-04679-3.
- ^ Паис, А. (1982). Тонкий Господь: Наука и жизнь Альберта Эйнштейна . Oxford University Press. ISBN 978-0-19-520438-4.
- ^ "Резолюция 1 15-й ГКМВ". BIPM . 1967. Архивировано из оригинала 11 апреля 2021 г. Получено 14 марта 2021 г.
- ^ "Резолюция 6 15-й ГКМВ". BIPM . 1967. Получено 13 октября 2010 г.
- ^ Barger, R.; Hall, J. (1973). "Длина волны 3,39-мкм линии поглощения метана, насыщенной лазером". Applied Physics Letters . 22 (4): 196. Bibcode : 1973ApPhL..22..196B. doi : 10.1063/1.1654608. S2CID 1841238.
- ^ "Резолюция 2 15-й ГКМВ". BIPM. 1975. Получено 9 сентября 2009 .
- ^ Тейлор, Э. Ф.; Уилер , Дж. А. (1992). Физика пространства-времени: Введение в специальную теорию относительности (2-е изд.). Macmillan. стр. 59. ISBN 978-0-7167-2327-1.
- ^ Пензес, В. Б. (2009). "Временная шкала для определения метра" (PDF) . NIST . Получено 11 января 2010 г. .
- ^ Адамс, С. (1997). Относительность: Введение в физику пространства–времени. CRC Press. стр. 140. ISBN 978-0-7484-0621-0.
Одним из специфических следствий этой системы определений является то, что любое будущее усовершенствование нашей способности измерять c не изменит скорость света (которая является определенным числом), но изменит длину метра!
- ^ Риндлер, В. (2006). Относительность: специальная, общая и космологическая (2-е изд.). Oxford University Press. стр. 41. ISBN 978-0-19-856731-8.
Обратите внимание, что [...] улучшение экспериментальной точности изменит показания счетчика относительно атомных длин волн, но не значение скорости света!
- ^ "Формулировка "явной константы"". BIPM . 2011. Архивировано из оригинала 11 августа 2014 года.
- ^ См., например:
- Коновер, Эмили (2 ноября 2016 г.). «Единицы измерения получают фундаментальное обновление». Science News . Получено 6 февраля 2022 г. .
- Knotts, Sandra; Mohr, Peter J.; Phillips, William D. (январь 2017 г.). «Введение в новую SI». The Physics Teacher . 55 (1): 16–21. Bibcode : 2017PhTea..55...16K. doi : 10.1119/1.4972491. ISSN 0031-921X. S2CID 117581000.
- «Переопределение SI». Национальный институт стандартов и технологий . 11 мая 2018 г. Получено 6 февраля 2022 г.
Дальнейшее чтение
Исторические справки
- Рёмер, О. (1676 г.). «Демонстрация трогательного движения светового потока М. Рёмера из Королевской академии наук» (PDF) . Journal des sçavans (на французском языке): 223–236. Архивировано из оригинала (PDF) 8 сентября 2022 года . Проверено 10 марта 2020 г.
- Переводится как «Демонстрация, касающаяся движения света». Philosophical Transactions of the Royal Society . 12 (136): 893–894. 1677. Bibcode :1677RSPT...12..893.. doi : 10.1098/rstl.1677.0024 . Архивировано из оригинала 29 июля 2007 г.
- Галлей, Э. (1694). «Господин Кассини, его новые и точные таблицы затмений первого спутника Юпитера, приведенные к юлианскому стилю и лондонскому меридиану». Philosophical Transactions of the Royal Society . 18 (214): 237–256. Bibcode : 1694RSPT...18..237C. doi : 10.1098/rstl.1694.0048 .
- Физо, HL (1849 г.). «Sur une expérience относительного опыта распространения света» (PDF) . Comptes rendus de l'Académie des Sciences (на французском языке). 29 : 90–92, 132.
- Фуко, JL (1862). «Экспериментальное определение света: параллакс дю Солей». Comptes rendus de l'Académie des Sciences (на французском языке). 55 : 501–503, 792–796.
- Майкельсон, А.А. (1878). «Экспериментальное определение скорости света». Труды Американской ассоциации содействия развитию науки . 27 : 71–77.
- Майкельсон, А.А.; Пиз, Ф.Г .; Пирсон, Ф. (1935). «Измерение скорости света в частичном вакууме». Astrophysical Journal . 82 (2091): 26–61. Bibcode : 1935ApJ....82...26M. doi : 10.1086/143655. PMID 17816642. S2CID 123010613.
- Ньюкомб, С. (1886). «Скорость света». Nature . 34 (863): 29–32. Bibcode : 1886Natur..34...29.. doi : 10.1038/034029c0 .
- Перротен, Дж. (1900). «Сюр ля витесс де ла свет». Comptes rendus de l'Académie des Sciences (на французском языке). 131 : 731–734.
Современные ссылки
- Бриллюэн, Л. (1960). Распространение волн и групповая скорость . Academic Press .
- Джексон, Дж. Д. (1975). Классическая электродинамика (2-е изд.). John Wiley & Sons. ISBN 978-0-471-30932-1.
- Кайзер, Г. (2000). Волоконно-оптическая связь (3-е изд.). McGraw-Hill. стр. 32. ISBN 978-0-07-232101-2.
- Ng, YJ (2004). "Квантовая пена и феноменология квантовой гравитации". В Amelino-Camelia, G; Kowalski-Glikman, J (ред.). Эффекты масштаба Планка в астрофизике и космологии . Springer. стр. 321 и далее. ISBN 978-3-540-25263-4.
- Helmcke, J.; Riehle, F. (2001). "Физика за определением метра". В Quinn, TJ; Leschiutta, S.; Tavella, P. (ред.). Последние достижения в метрологии и фундаментальных константах . IOS Press . стр. 453. ISBN 978-1-58603-167-1.
- Дафф, М.Дж. (2004). "Комментарий к изменению во времени фундаментальных констант". arXiv : hep-th/0208093 .
Внешние ссылки
- «Тест скорости света в вакуумной трубке длиной в милю». Popular Science Monthly , сентябрь 1930 г., стр. 17–18.
- Определение метра (Международное бюро мер и весов, BIPM)
- Скорость света в вакууме (Национальный институт стандартов и технологий, NIST)
- Галерея данных: Скорость света по Майкельсону (одномерная оценка местоположения) (загрузить данные, собранные Альбертом А. Майкельсоном )
- Subluminal (Java-апплет Грега Эгана, демонстрирующий ограничения информации о групповой скорости)
- Небольшое обсуждение сложения скоростей
- Скорость света (Шестьдесят символов, Физический факультет Ноттингемского университета [видео])
- Скорость света, обсуждение на BBC Radio 4 ( In Our Time , 30 ноября 2006 г.)
- Скорость света (Live-Counter – Иллюстрации)
- Скорость света – анимированные демонстрации
- «Скорость света», Альберт А. Николсон, Scientific American , 28 сентября 1878 г., стр. 193






