Магнитный момент
| Статьи о |
| Электромагнетизм |
|---|
 |
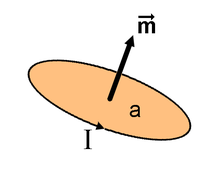 Магнитный момент m тока I , охватывающего площадь а . | |
Общие символы | м |
|---|---|
| единица СИ | Ампер - метр 2 |
| В основных единицах СИ | м 2 ⋅ А |
| Измерение | Л 2 Я |
В электромагнетизме магнитный момент или магнитный дипольный момент — это комбинация силы и ориентации магнита или другого объекта или системы, которая создает магнитное поле . Магнитный дипольный момент объекта определяет величину крутящего момента, который объект испытывает в данном магнитном поле. Когда применяется то же самое магнитное поле, объекты с большими магнитными моментами испытывают большие крутящие моменты. Сила (и направление) этого крутящего момента зависит не только от величины магнитного момента, но и от его ориентации относительно направления магнитного поля. Его направление указывает от южного полюса к северному полюсу магнита (т. е. внутри магнита).
Магнитный момент также выражает магнитное силовое воздействие магнита. Магнитное поле магнитного диполя пропорционально его магнитному дипольному моменту. Дипольная составляющая магнитного поля объекта симметрична относительно направления его магнитного дипольного момента и уменьшается обратно пропорционально кубу расстояния от объекта.
Примерами объектов или систем, которые создают магнитные моменты, являются: постоянные магниты; астрономические объекты, такие как многие планеты , включая Землю , а также некоторые луны , звезды и т. д.; различные молекулы ; элементарные частицы (например, электроны ); композиты элементарных частиц ( протоны и нейтроны — как ядра атома); и контуры электрического тока , такие как создаваемые электромагнитами .
Определение, единицы и измерения
Определение
Магнитный момент можно определить как вектор (на самом деле псевдовектор ), связывающий выравнивающий крутящий момент на объекте от внешнего приложенного магнитного поля с самим вектором поля. Соотношение задается формулой: [1] где τ — крутящий момент, действующий на диполь, B — внешнее магнитное поле, а m — магнитный момент.
Это определение основано на том, как можно было бы, в принципе, измерить магнитный момент неизвестного образца. Для контура тока это определение приводит к величине магнитного дипольного момента, равной произведению тока на площадь контура. Кроме того, это определение позволяет вычислить ожидаемый магнитный момент для любого известного макроскопического распределения тока.
Альтернативное определение полезно для термодинамических расчетов магнитного момента. В этом определении магнитный дипольный момент системы представляет собой отрицательный градиент ее собственной энергии, U int , по отношению к внешнему магнитному полю:
В общем случае внутренняя энергия включает энергию собственного поля системы плюс энергию внутренних процессов системы. Например, для атома водорода в состоянии 2p во внешнем поле энергия собственного поля незначительна, поэтому внутренняя энергия по сути является собственной энергией состояния 2p, которая включает кулоновскую потенциальную энергию и кинетическую энергию электрона. Энергия поля взаимодействия между внутренними диполями и внешними полями не является частью этой внутренней энергии. [2]
Единицы
Единицей магнитного момента в Международной системе единиц ( СИ) является А⋅м 2 , где А — ампер (единица силы тока в СИ), а м — метр (единица расстояния в СИ). Эта единица имеет эквиваленты в других производных единицах СИ, включая: [3] [4]
где N — ньютон (единица силы, полученная в системе СИ), T — тесла (единица плотности магнитного потока, полученная в системе СИ), а J — джоуль (единица энергии , полученная в системе СИ ). [5] : 20–21 Хотя крутящий момент (Н·м) и энергия (Дж) имеют эквивалентные размеры, крутящие моменты никогда не выражаются в единицах энергии. [5] : 23
В системе СГС существует несколько различных наборов единиц электромагнетизма, из которых основными являются ESU , Gaussian и EMU . Среди них есть две альтернативные (неэквивалентные) единицы магнитного дипольного момента:
где statA — это статимпер , cm — это сантиметр , erg — это эрг , а G — это гаусс . Отношение этих двух неэквивалентных единиц СГС (EMU/ESU) равно скорости света в свободном пространстве, выраженной в см ⋅ с −1 .
Все формулы в этой статье верны в единицах СИ ; их может потребоваться изменить для использования в других системах единиц. Например, в единицах СИ контур тока с током I и площадью A имеет магнитный момент IA (см. ниже), но в гауссовых единицах магнитный момент равен Я/с .
Другими единицами измерения магнитного дипольного момента являются магнетон Бора и ядерный магнетон .
Измерение
Магнитные моменты объектов обычно измеряются с помощью устройств, называемых магнитометрами , хотя не все магнитометры измеряют магнитный момент: некоторые из них настроены на измерение магнитного поля . Однако, если магнитное поле, окружающее объект, известно достаточно хорошо, то магнитный момент можно рассчитать из этого магнитного поля. [ необходима цитата ]
Отношение к намагничиванию
Магнитный момент — это величина, которая описывает магнитную силу всего объекта. Иногда, однако, полезно или необходимо знать, какая часть чистого магнитного момента объекта создается определенной частью этого магнита. Поэтому полезно определить поле намагничивания M как: где m Δ V и V Δ V — магнитный дипольный момент и объем достаточно малой части магнита Δ V . Это уравнение часто представляется с использованием производной записи, такой что где d m — элементарный магнитный момент, а d V — элемент объема . Чистый магнитный момент магнита m, следовательно, равен , где тройной интеграл обозначает интегрирование по объему магнита . Для однородного намагничивания (когда и величина, и направление M одинаковы для всего магнита (например, прямого стержневого магнита) последнее уравнение упрощается до: где V — объем стержневого магнита.
Намагниченность часто не указывается как материальный параметр для коммерчески доступных ферромагнитных материалов. Вместо этого указан параметр остаточной магнитной индукции (или остаточная индукция), обозначаемый как B r . Формула, необходимая в этом случае для расчета m в (единицах А⋅м 2 ), выглядит следующим образом:
где:
- B r — остаточная плотность потока, выраженная в теслах .
- V — объем магнита (в м3 ) .
- μ 0 — проницаемость вакуума (4π × 10−7 Гн/м ). [ 6]
Модели
Предпочтительное классическое объяснение магнитного момента со временем изменилось. До 1930-х годов учебники объясняли момент с помощью гипотетических магнитных точечных зарядов. С тех пор большинство определяло его в терминах токов Ампера. [7] В магнитных материалах причиной магнитного момента являются состояния спина и орбитального углового момента электронов , и они различаются в зависимости от того, выровнены ли атомы в одной области с атомами в другой. [ требуется ссылка ]
Модель магнитного полюса
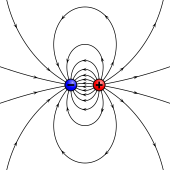
Источники магнитных моментов в материалах могут быть представлены полюсами по аналогии с электростатикой . Иногда это называют моделью Гилберта. [8] : 258 В этой модели небольшой магнит моделируется парой фиктивных магнитных монополей одинаковой величины, но противоположной полярности . Каждый полюс является источником магнитной силы, которая ослабевает с расстоянием. Поскольку магнитные полюса всегда идут парами, их силы частично компенсируют друг друга, потому что в то время как один полюс тянет, другой отталкивает. Это погашение является наибольшим, когда полюса находятся близко друг к другу, т. е. когда стержневой магнит короткий. Магнитная сила, создаваемая стержневым магнитом в данной точке пространства, поэтому зависит от двух факторов: силы p его полюсов ( силы магнитного полюса ) и вектора, разделяющего их. Магнитный дипольный момент m связан с фиктивными полюсами как [7]
Он указывает в направлении от Южного к Северному полюсу. Аналогию с электрическими диполями не следует заходить слишком далеко, поскольку магнитные диполи связаны с угловым моментом (см. Связь с угловым моментом). Тем не менее, магнитные полюса очень полезны для магнитостатических расчетов, особенно в приложениях к ферромагнетикам . [7] Практики , использующие подход магнитных полюсов, обычно представляют магнитное поле безвихревым полем H , по аналогии с электрическим полем E.
Модель петли Ампера

После того, как Ганс Христиан Эрстед открыл, что электрические токи создают магнитное поле, а Андре-Мари Ампер обнаружил, что электрические токи притягиваются и отталкиваются друг от друга подобно магнитам, было естественно выдвинуть гипотезу, что все магнитные поля обусловлены электрическими токовыми петлями. В этой модели, разработанной Ампером, элементарный магнитный диполь, из которого состоят все магниты, представляет собой достаточно малую амперовую петлю тока I. Дипольный момент этой петли равен , где S — площадь петли. Направление магнитного момента — это направление, нормальное к области, охватываемой током, в соответствии с направлением тока с использованием правила правой руки.
Локализованные распределения тока

Магнитный дипольный момент можно рассчитать для локализованного (не простирающегося до бесконечности) распределения тока, предполагая, что мы знаем все вовлеченные токи. Традиционно вывод начинается с мультипольного разложения векторного потенциала . Это приводит к определению магнитного дипольного момента как: где × — векторное векторное произведение , r — радиус-вектор, а j — плотность электрического тока , а интеграл — объемный интеграл. [9] : § 5.6 Когда плотность тока в интеграле заменяется петлей тока I в плоскости, охватывающей область S, то объемный интеграл становится линейным интегралом , а результирующий дипольный момент становится , что и является способом получения магнитного дипольного момента для амперовой петли.
Практики , использующие модель токовой петли, обычно представляют магнитное поле соленоидальным полем B , аналогичным электростатическому полю D.
Магнитный момент соленоида

Обобщением вышеприведенной токовой петли является катушка, или соленоид . Ее момент является векторной суммой моментов отдельных витков. Если соленоид имеет N одинаковых витков (однослойная обмотка) и векторную площадь S ,
Квантово-механическая модель
При расчете магнитных моментов материалов или молекул на микроскопическом уровне часто бывает удобно использовать третью модель для магнитного момента, которая использует линейную связь между угловым моментом и магнитным моментом частицы. Хотя это соотношение легко вывести для макроскопических токов с помощью модели амперовой петли (см. ниже), ни модель магнитного полюса, ни модель амперовой петли не отражают в действительности то, что происходит на атомном и молекулярном уровнях. На этом уровне необходимо использовать квантовую механику . К счастью, линейная связь между магнитным дипольным моментом частицы и ее угловым моментом все еще сохраняется, хотя она различна для каждой частицы. Кроме того, необходимо соблюдать осторожность, чтобы различать собственный угловой момент (или спин ) частицы и орбитальный угловой момент частицы. Более подробную информацию см. ниже.
Воздействие внешнего магнитного поля
Крутящий момент на момент
Крутящий момент τ на объекте, имеющем магнитный дипольный момент m в однородном магнитном поле B, равен:
Это справедливо на данный момент из-за любого локализованного распределения тока при условии, что магнитное поле однородно. Для неоднородного B уравнение также справедливо для крутящего момента вокруг центра магнитного диполя при условии, что магнитный диполь достаточно мал. [8] : 257
Электрон, ядро или атом, помещенные в однородное магнитное поле, будут прецессировать с частотой, известной как частота Лармора . См. Резонанс .
Сила на мгновение
Магнитный момент во внешнем магнитном поле имеет потенциальную энергию U :
В случае, когда внешнее магнитное поле неоднородно, будет существовать сила, пропорциональная градиенту магнитного поля , действующая на сам магнитный момент. Существуют два выражения для силы, действующей на магнитный диполь, в зависимости от того, является ли модель, используемая для диполя , токовой петлей или двумя монополями (аналогично электрическому диполю). [10] Сила, полученная в случае модели токовой петли, равна
Предполагая существование магнитного монополя, сила модифицируется следующим образом:
В случае использования пары монополей (т.е. модели электрического диполя) сила равна И одна из них может быть выражена через другую с помощью соотношения
Во всех этих выражениях m — диполь, а B — магнитное поле в его положении. Обратите внимание, что если нет токов или изменяющихся во времени электрических полей или магнитного заряда, ∇× B = 0 , ∇⋅ B = 0 и два выражения согласуются.
Отношение к свободной энергии
Можно связать магнитный момент системы со свободной энергией этой системы. [11] В однородном магнитном поле B свободная энергия F может быть связана с магнитным моментом M системы следующим образом: где S — энтропия системы, а T — температура. Следовательно, магнитный момент также можно определить в терминах свободной энергии системы как
Магнетизм
Кроме того, приложенное магнитное поле может изменить магнитный момент самого объекта; например, намагничивая его. Это явление известно как магнетизм . Приложенное магнитное поле может переворачивать магнитные диполи, из которых состоит материал, вызывая как парамагнетизм , так и ферромагнетизм . Кроме того, магнитное поле может влиять на токи, которые создают магнитные поля (например, атомные орбиты), что вызывает диамагнетизм .
Воздействие на окружающую среду
Магнитное поле магнитного момента

Любая система, обладающая чистым магнитным дипольным моментом m, будет создавать дипольное магнитное поле (описанное ниже) в пространстве, окружающем систему. Хотя чистое магнитное поле, создаваемое системой, может также иметь мультипольные компоненты более высокого порядка, они будут падать с расстоянием быстрее, так что только дипольный компонент будет доминировать в магнитном поле системы на больших расстояниях от нее.
Магнитное поле магнитного диполя зависит от силы и направления магнитного момента магнита, но убывает пропорционально кубу расстояния, так что:
где - магнитное поле, создаваемое магнитом, а - вектор от центра магнитного диполя до места, где измеряется магнитное поле. Обратную кубическую природу этого уравнения легче увидеть, выразив вектор местоположения как произведение его величины на единичный вектор в его направлении ( ), так что:
Эквивалентные уравнения для магнитного поля те же самые, за исключением мультипликативного множителя μ 0 =4 π × 10−7 H / m , где μ 0 известно как проницаемость вакуума . Например:
Силы между двумя магнитными диполями
Как обсуждалось ранее, сила, действующая со стороны дипольной петли с моментом m 1 на другую с моментом m 2, равна где B 1 — магнитное поле, вызванное моментом m 1 . Результатом вычисления градиента является [12] [13] где r̂ — единичный вектор, направленный от магнита 1 к магниту 2, а r — расстояние. Эквивалентное выражение — [13] Сила, действующая на m 1 , направлена в противоположном направлении.
Крутящий момент одного магнитного диполя на другой
Крутящий момент магнита 1 на магните 2 равен
Теория, лежащая в основе магнитных диполей
Магнитное поле любого магнита можно смоделировать серией членов, для которых каждый член сложнее (имеет более тонкие угловые детали), чем предыдущий. Первые три члена этой серии называются монополем ( представленным изолированным магнитным северным или южным полюсом), диполем ( представленным двумя равными и противоположными магнитными полюсами) и квадруполем (представленным четырьмя полюсами, которые вместе образуют два равных и противоположных диполя). Величина магнитного поля для каждого члена уменьшается прогрессивно быстрее с расстоянием, чем для предыдущего члена, так что на достаточно больших расстояниях первый ненулевой член будет доминировать. [ необходима цитата ]
Для многих магнитов первым ненулевым членом является магнитный дипольный момент. (На сегодняшний день не было экспериментально обнаружено ни одного изолированного магнитного монополя .) Магнитный диполь является пределом либо токовой петли, либо пары полюсов, поскольку размеры источника уменьшаются до нуля, а момент остается постоянным. Пока эти пределы применяются только к полям, далеким от источников, они эквивалентны. Однако эти две модели дают разные предсказания для внутреннего поля (см. ниже).
Магнитные потенциалы
Традиционно уравнения для магнитного дипольного момента (и членов более высокого порядка) выводятся из теоретических величин, называемых магнитными потенциалами [9] : § 5.6 , с которыми проще иметь дело математически, чем с магнитными полями. [ необходима ссылка ]
В модели магнитного полюса соответствующее магнитное поле является размагничивающим полем . Поскольку размагничивающая часть не включает, по определению, часть из- за свободных токов, существует магнитный скалярный потенциал такой, что
В модели амперовой петли соответствующим магнитным полем является магнитная индукция . Поскольку магнитные монополи не существуют, существует магнитный векторный потенциал такой, что
Оба эти потенциала могут быть рассчитаны для любого произвольного распределения тока (для модели петли Ампера) или распределения магнитного заряда (для модели магнитного заряда) при условии, что они ограничены достаточно малой областью, чтобы дать: где — плотность тока в модели петли Ампера, — плотность напряженности магнитного полюса по аналогии с плотностью электрического заряда , которая приводит к электрическому потенциалу, а интегралы — объемные (тройные) интегралы по координатам, составляющим . Знаменатели этих уравнений можно разложить с помощью мультипольного разложения, чтобы получить ряд членов, которые имеют большую степень расстояний в знаменателе. Поэтому первый ненулевой член будет доминировать для больших расстояний. Первый ненулевой член для векторного потенциала: где — это: где × — векторное векторное произведение , r — радиус-вектор, а j — плотность электрического тока , а интеграл — объемный интеграл.
С точки зрения магнитного полюса первый ненулевой член скалярного потенциала равен
Здесь это можно представить в терминах плотности напряженности магнитного полюса, но более полезно выразить в терминах поля намагничивания следующим образом:
Для обоих уравнений используется один и тот же символ, поскольку они дают эквивалентные результаты за пределами магнита.
Внешнее магнитное поле, создаваемое магнитным дипольным моментом
Плотность магнитного потока для магнитного диполя в модели амперной петли, таким образом, равна
Далее, напряженность магнитного поля равна
Внутреннее магнитное поле диполя
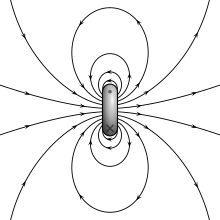
Две модели для диполя (магнитные полюса или токовая петля) дают одинаковые прогнозы для магнитного поля вдали от источника. Однако внутри области источника они дают разные прогнозы. Магнитное поле между полюсами (см. рисунок для модели магнитного полюса) имеет противоположное направление к магнитному моменту (который указывает от отрицательного заряда к положительному заряду), в то время как внутри токовой петли оно имеет то же направление (см. рисунок справа). Пределы этих полей также должны быть разными, поскольку источники сжимаются до нулевого размера. Это различие имеет значение только в том случае, если дипольный предел используется для расчета полей внутри магнитного материала. [7]
Если магнитный диполь образован путем взятия «северного полюса» и «южного полюса», сближения их друг с другом, но сохранения постоянным произведения заряда магнитного полюса и расстояния, то предельное поле равно [7]
Если магнитный диполь формируется путем уменьшения и уменьшения контура тока, но при этом произведение тока и площади остается постоянным, то предельное поле равно В отличие от выражений в предыдущем разделе, этот предел верен для внутреннего поля диполя. [7] [9] : 184
Эти поля связаны соотношением B = μ 0 ( H + M ) , где M ( r ) = m δ ( r ) — намагниченность .
Отношение к моменту импульса
Магнитный момент тесно связан с угловым моментом, называемым гиромагнитным эффектом . Этот эффект выражается в макроскопическом масштабе в эффекте Эйнштейна-де Гааза , или «вращении за счет намагничивания», и его обратном эффекте, эффекте Барнетта , или «намагничивании за счет вращения». [1] Кроме того, крутящий момент , приложенный к относительно изолированному магнитному диполю, такому как атомное ядро, может заставить его прецессировать (вращаться вокруг оси приложенного поля). Это явление используется в ядерном магнитном резонансе . [ требуется ссылка ]
Рассмотрение магнитного диполя как контура тока выявляет тесную связь между магнитным моментом и угловым моментом. Поскольку частицы, создающие ток (вращаясь вокруг контура), имеют заряд и массу, как магнитный момент, так и угловой момент увеличиваются со скоростью вращения. Отношение этих двух величин называется гиромагнитным отношением или так: [14] [15] где — угловой момент частицы или частиц, создающих магнитный момент.
В модели амперовой петли, которая применяется для макроскопических токов, гиромагнитное отношение равно половине отношения заряда к массе . Это можно показать следующим образом. Угловой момент движущейся заряженной частицы определяется как: где μ — масса частицы, а v — скорость частицы . Угловой момент очень большого числа заряженных частиц, составляющих ток, таким образом, равен: где ρ — плотность массы движущихся частиц. По соглашению направление векторного произведения задается правилом правой руки . [16]
Это похоже на магнитный момент, создаваемый очень большим числом заряженных частиц, составляющих этот ток: где и — плотность заряда движущихся заряженных частиц.
Сравнение двух уравнений дает: где — заряд частицы, — масса частицы.
Хотя атомные частицы не могут быть точно описаны как вращающиеся (и вращающиеся) распределения заряда с равномерным отношением заряда к массе, эту общую тенденцию можно наблюдать в атомном мире, так что: где g -фактор зависит от частицы и конфигурации. Например, g -фактор для магнитного момента, обусловленного вращением электрона вокруг ядра, равен единице, в то время как g -фактор для магнитного момента электрона, обусловленного его собственным угловым моментом ( спином ), немного больше 2. G -фактор атомов и молекул должен учитывать орбитальные и собственные моменты его электронов и, возможно, также собственный момент его ядер.
В атомном мире угловой момент ( спин ) частицы — это целое число (или полуцелое число в случае фермионов), кратное приведенной постоянной Планка ħ . Это основа для определения единиц магнитного момента магнетона Бора (предполагая отношение заряда к массе электрона ) и ядерного магнетона (предполагая отношение заряда к массе протона ). Подробнее см. магнитный момент электрона и магнетон Бора .
Атомы, молекулы и элементарные частицы
По сути, вклад в магнитный момент любой системы может исходить от источников двух видов: 1) движение электрических зарядов , таких как электрические токи ; и 2) внутренний магнетизм, обусловленный спином элементарных частиц , таких как электрон . [ необходима ссылка ]
Вклад источников первого рода можно рассчитать, зная распределение всех электрических токов (или, альтернативно, всех электрических зарядов и их скоростей) внутри системы, используя приведенные ниже формулы.
Вклады, обусловленные спином частицы, суммируют величину собственного магнитного момента каждой элементарной частицы, фиксированное число, часто измеряемое экспериментально с большой точностью. Например, любой магнитный момент электрона измеряется как−9,284 764 × 10 −24 Дж/Тл . [17] Направление магнитного момента любой элементарной частицы полностью определяется направлением ее спина , причем отрицательное значение указывает на то , что магнитный момент любого электрона антипараллелен его спину.
Чистый магнитный момент любой системы представляет собой векторную сумму вкладов от одного или обоих типов источников. Например, магнитный момент атома водорода-1 (легчайший изотоп водорода, состоящий из протона и электрона) представляет собой векторную сумму следующих вкладов:
- собственный момент электрона,
- орбитальное движение электрона вокруг протона,
- собственный момент протона.
Аналогично, магнитный момент стержневого магнита представляет собой сумму вносящих вклад магнитных моментов, которые включают собственные и орбитальные магнитные моменты неспаренных электронов материала магнита, а также ядерные магнитные моменты.
Магнитный момент атома
Для атома отдельные электронные спины складываются, чтобы получить полный спин, а отдельные орбитальные угловые моменты складываются, чтобы получить полный орбитальный угловой момент. Затем эти два момента складываются с использованием связи углового момента , чтобы получить полный угловой момент. Для атома без ядерного магнитного момента величина атомного дипольного момента, , тогда [18] где j - квантовое число полного углового момента , g J - g -фактор Ланде , а μ B - магнетон Бора . Компонента этого магнитного момента вдоль направления магнитного поля тогда [19]
Знак «минус» возникает из-за того, что электроны имеют отрицательный заряд.
Целое число m (не путать с моментом, ) называется магнитным квантовым числом или экваториальным квантовым числом, которое может принимать любое из 2 j + 1 значений: [20]
Из-за углового момента динамика магнитного диполя в магнитном поле отличается от динамики электрического диполя в электрическом поле. Поле действительно оказывает крутящий момент на магнитный диполь, стремясь выровнять его с полем. Однако крутящий момент пропорционален скорости изменения углового момента, поэтому происходит прецессия : направление спина меняется. Такое поведение описывается уравнением Ландау–Лифшица–Гильберта : [21] [22] где γ — гиромагнитное отношение , m — магнитный момент, λ — коэффициент затухания, а H eff — эффективное магнитное поле (внешнее поле плюс любое самоиндуцированное поле). Первый член описывает прецессию момента вокруг эффективного поля, в то время как второй — затухающий член, связанный с диссипацией энергии, вызванной взаимодействием с окружающей средой.
Магнитный момент электрона
Электроны и многие элементарные частицы также имеют собственные магнитные моменты, объяснение которых требует квантово-механического рассмотрения и связано с собственным угловым моментом частиц, как обсуждалось в статье Электронный магнитный момент . Именно эти собственные магнитные моменты приводят к макроскопическим эффектам магнетизма и другим явлениям, таким как электронный парамагнитный резонанс . [ необходима цитата ]
Магнитный момент электрона равен , где μ B — магнетон Бора , S — спин электрона , а g -фактор g S равен 2 согласно теории Дирака , но из-за квантово-электродинамических эффектов в действительности он немного больше: 2,002 319 304 36. Отклонение от 2 известно как аномальный магнитный дипольный момент .
Опять же, важно отметить, что m — отрицательная константа, умноженная на спин , поэтому магнитный момент электрона антипараллелен спину. Это можно понять с помощью следующей классической картины: если мы представим, что момент импульса спина создается вращением массы электрона вокруг некоторой оси, то электрический ток, который создает это вращение, циркулирует в противоположном направлении из-за отрицательного заряда электрона; такие токовые петли создают магнитный момент, который антипараллелен спину. Следовательно, для позитрона (античастицы электрона) магнитный момент параллелен его спину.
Магнитный момент ядра
Ядерная система — это сложная физическая система, состоящая из нуклонов, т. е. протонов и нейтронов . Квантово-механические свойства нуклонов включают спин среди прочих. Поскольку электромагнитные моменты ядра зависят от спина отдельных нуклонов, можно рассмотреть эти свойства с помощью измерений ядерных моментов, а точнее ядерного магнитного дипольного момента.
Большинство распространенных ядер существуют в своем основном состоянии , хотя ядра некоторых изотопов имеют долгоживущие возбужденные состояния . Каждое энергетическое состояние ядра данного изотопа характеризуется четко определенным магнитным дипольным моментом, величина которого является фиксированным числом, часто измеряемым экспериментально с большой точностью. Это число очень чувствительно к индивидуальным вкладам нуклонов, и измерение или предсказание его значения может раскрыть важную информацию о содержании ядерной волновой функции. Существует несколько теоретических моделей, которые предсказывают значение магнитного дипольного момента, и ряд экспериментальных методов, направленных на проведение измерений в ядрах вдоль ядерной диаграммы.
Магнитный момент молекулы
Любая молекула имеет четко определенную величину магнитного момента, которая может зависеть от энергетического состояния молекулы . Как правило, общий магнитный момент молекулы представляет собой комбинацию следующих вкладов, в порядке их типичной силы:
- магнитные моменты, обусловленные его неспаренными электронными спинами ( парамагнитный вклад), если таковые имеются
- орбитальное движение его электронов, которое в основном состоянии часто пропорционально внешнему магнитному полю ( диамагнитный вклад)
- объединенный магнитный момент его ядерных спинов , который зависит от конфигурации ядерного спина .
Примеры молекулярного магнетизма
- Молекула дикислорода O2 проявляет сильный парамагнетизм из - за неспаренных спинов двух ее внешних электронов.
- Молекула диоксида углерода , CO 2 , в основном проявляет диамагнетизм , гораздо более слабый магнитный момент электронных орбиталей , который пропорционален внешнему магнитному полю. Ядерный магнетизм магнитного изотопа, такого как 13 C или 17 O, будет способствовать магнитному моменту молекулы.
- Молекула диводорода H2 в слабом (или нулевом) магнитном поле проявляет ядерный магнетизм и может находиться в пара- или орто- ядерной спиновой конфигурации .
- Многие комплексы переходных металлов являются магнитными. Формула, учитывающая только спин, является хорошим первым приближением для высокоспиновых комплексов переходных металлов первого ряда . [23]
| Число неспаренных электронов | Момент , зависящий только от спина ( μ B ) |
|---|---|
| 1 | 1.73 |
| 2 | 2.83 |
| 3 | 3.87 |
| 4 | 4.90 |
| 5 | 5.92 |
Элементарные частицы
В атомной и ядерной физике греческий символ μ представляет величину магнитного момента, часто измеряемого в магнетонах Бора или ядерных магнетонах , связанного с собственным спином частицы и/или с орбитальным движением частицы в системе. Значения собственных магнитных моментов некоторых частиц приведены в таблице ниже:
| Имя частицы (символ) | Магнитный дипольный момент (10−27 Дж ⋅ Тл − 1 ) | Спиновое квантовое число ( безразмерное ) |
|---|---|---|
| электрон (е − ) | −9 284 .764 | 1/2 |
| протон (H + ) | –0 014.106 067 | 1/2 |
| нейтрон (н) | 0 00−9,662 36 | 1/2 |
| мюон (μ − ) | 0 0−44,904 478 | 1/2 |
| дейтрон ( 2 H + ) | –0 004.330 7346 | 1 |
| тритон ( 3 H + ) | –0 015.046 094 | 1/2 |
| гелион ( 3 He ++ ) | 0 0−10,746 174 | 1/2 |
| альфа - частица ( 4He ++ ) | –0 00 0 | 0 |
Смотрите также
- Порядки величины (магнитный момент)
- Момент (физика)
- Электрический дипольный момент
- Тороидальный дипольный момент
- Магнитная восприимчивость
- Орбитальное намагничивание
- Магнитное диполь-дипольное взаимодействие
Ссылки и примечания
- ^ ab Каллити, Б. Д.; Грэм, К. Д. (2008). Введение в магнитные материалы (2-е изд.). Wiley-IEEE Press . стр. 103. ISBN 978-0-471-47741-9.
- ^ См., например, Callen, Herbert B. (1985). Термодинамика и введение в термостатистику (2-е изд.). John Wiley & Sons . стр. 200. ISBN 978-0-471-86256-7.где соответствующее U — это U[B e ] .
- ^ "Магнитные единицы". IEEE Magnetics . Получено 19 февраля 2016 г.
- ^ Mohr, Peter J.; Newell, David B.; Taylor, Barry N. (21 июля 2015 г.). "CODATA Recommended Values of the Fundamental Physical Constants: 2014". Reviews of Modern Physics . 88 (3): 035009. arXiv : 1507.07956 . Bibcode : 2016RvMP...88c5009M. doi : 10.1103/RevModPhys.88.035009. S2CID 1115862.
- ^ ab Международная система единиц (PDF) (9-е изд.), Международное бюро мер и весов, декабрь 2022 г., ISBN 978-92-822-2272-0
- ^ "K&J Magnetics – Глоссарий". www.kjmagnetics.com .
- ^ abcdef Браун, Уильям Фуллер-младший (1962). Магнитостатические принципы в ферромагнетизме . Северная Голландия .
- ^ ab Гриффитс, Дэвид Дж. (1999). Введение в электродинамику (3-е изд.). Prentice Hall . стр. 258. ISBN 978-0-13-805326-0. OCLC 40251748.
- ^ abc Джексон, Джон Дэвид (1975). Классическая электродинамика (2-е изд.). Wiley. ISBN 978-0-471-43132-9.
- ^ Бойер, Тимоти Х. (1988). «Сила, действующая на магнитный диполь». Am. J. Phys. 56 (8): 688–692. Bibcode : 1988AmJPh..56..688B. doi : 10.1119/1.15501.
- ^ Ландау, Л. Д.; Лифшиц, Е. М.; Питаевский, Л. П. (15 января 1984 г.). Электродинамика сплошных сред: Том 8 (Курс теоретической физики) (2-е изд.). Butterworth-Heinemann. стр. 130. ISBN 978-0-7506-2634-7.
- ^ Фурлани, Эдвард П. (2001). Постоянные магниты и электромеханические устройства: материалы, анализ и применение. Academic Press . стр. 140. ISBN 978-0-12-269951-1.
- ^ ab Yung, KW; Landecker, PB; Villani, DD (1998). "Аналитическое решение для силы между двумя магнитными диполями" (PDF) . Magnetic and Electrical Separation . 9 : 39–52. doi : 10.1155/1998/79537 . Получено 24 ноября 2012 г. .
- ^ Крей, Уве; Оуэн, Энтони (2007). Основы теоретической физики. Springer . С. 151–152. ISBN 978-3-540-36804-5.
- ^ Бакстон, Ричард Б. (2002). Введение в функциональную магнитно-резонансную томографию. Cambridge University Press . стр. 136. ISBN 978-0-521-58113-4.
- ^ Фейнман, Ричард П .; Лейтон, Роберт Б .; Сэндс, Мэтью (2006). Лекции Фейнмана по физике . Том 2. Pearson/Addison-Wesley. С. 13–12. ISBN 978-0-8053-9045-2.
- ^ "Значение CODATA: магнитный момент электрона". physics.nist.gov .
- ^ Тилли, Р. Дж. Д. (2004). Понимание твердых тел. John Wiley and Sons . стр. 368. ISBN 978-0-470-85275-0.
- ^ Типлер, Пол Аллен; Ллевеллин, Ральф А. (2002). Современная физика (4-е изд.). Макмиллан . п. 310. ИСБН 978-0-7167-4345-3.
- ^ Crowther, JA (1949). Ионы, электроны и ионизирующие излучения (8-е изд.). Лондон: Edward Arnold. стр. 270.
- ^ Райс, Стюарт Алан (2004). Достижения в химической физике. Wiley . С. 208 и далее. ISBN 978-0-471-44528-9.
- ^ Штайнер, Маркус (2004). Микромагнетизм и электрическое сопротивление ферромагнитных электродов для устройств спиновой инжекции. Cuvillier Verlag. стр. 6. ISBN 978-3-86537-176-8.
- ^ Фиггис, Б. Н.; Льюис, Дж. (1960). «Магнетохимия комплексных соединений». В Льюис, Дж.; Уилкинс, РГ (ред.). Современная координационная химия: принципы и методы . Нью-Йорк: Interscience. стр. 405–407.
- ^ "Результаты поиска, соответствующие 'magnetic moment'". CODATA международные рекомендуемые значения фундаментальных физических констант . Национальный институт стандартов и технологий . Получено 11 мая 2012 г.
Внешние ссылки
- Боутелл, Ричард (2009). «μ – Магнитный момент». Шестьдесят символов . Брэди Харан для Ноттингемского университета .




















![{\displaystyle {\begin{aligned}\mathbf {F} _{\text{loop}}&=\left(\mathbf {m} \times \nabla \right)\times \mathbf {B} \\[1ex ]&=\nabla \left(\mathbf {m} \cdot \mathbf {B} \right)-\left(\nabla \cdot \mathbf {B} \right)\mathbf {m} \end{aligned}} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/c22e36b71b155bc4606afc9724584865e34aba25)













![{\displaystyle \mathbf {F} (\mathbf {r},\mathbf {m} _{1},\mathbf {m} _{2}) = {\frac {3\mu _{0}}{4 \pi |\mathbf {r} |^{4}}}\left[\mathbf {m} _{2}(\mathbf {m} _{1}\cdot {\hat {\mathbf {r} }} )+\mathbf {m} _{1}(\mathbf {m} _{2}\cdot {\hat {\mathbf {r} }})+{\hat {\mathbf {r} }}(\mathbf {m} _{1}\cdot \mathbf {m} _{2})-5{\hat {\mathbf {r} }}(\mathbf {m} _{1}\cdot {\hat {\mathbf {r} }})(\mathbf {m} _{2}\cdot {\hat {\mathbf {r} }}) \верно],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/36db486ff5913093bf0fcf45c99a9a97c4eb04f3)
![{\displaystyle \mathbf {F} = {\frac {3\mu _{0}}{4\pi |\mathbf {r} |^{4}}}\left[({\hat {\mathbf {r } }}\times \mathbf {m} _{1})\times \mathbf {m} _{2}+({\hat {\mathbf {r} }}\times \mathbf {m} _{2} )\times \mathbf {m} _{1}-2{\hat {\mathbf {r} }}(\mathbf {m} _{1}\cdot \mathbf {m} _{2})+5{ \hat {\mathbf {r} }}({\hat {\mathbf {r} }}\times \mathbf {m} _{1})\cdot ({\hat {\mathbf {r} }}\times \mathbf {m} _{2})\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/abb27738c84ba074e295ea8b18b25f0d12d607af)



![{\displaystyle {\begin{aligned}\mathbf {A} \left(\mathbf {r},t\right)&={\frac {\mu _{0}}{4\pi }}\int {\ frac {\mathbf {j} \left(\mathbf {r} '\right)}{\left|\mathbf {r} -\mathbf {r} '\right|}}\,\mathrm {d} V' ,\\[1ex]\psi \left(\mathbf {r} ,t\right)&= {\frac {1}{4\pi }}\int {\frac {\rho \left(\mathbf {r } '\right)}{\left|\mathbf {r} -\mathbf {r} '\right|}}\,\mathrm {d} V',\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d741e8baf5f1f001400efdf08c0f96efcab54887)









![{\displaystyle \mathbf {H} (\mathbf {r}) = {\frac {1}{4\pi }}\left[{\frac {3\mathbf {\hat {r}} (\mathbf {\ шляпа {r}} \cdot \mathbf {m} )-\mathbf {m} }{|\mathbf {r} |^{3}}}-{\frac {4\pi }{3}}\mathbf { m} \delta (\mathbf {r} )\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a1b635de5e52b7fd68571a72866d50392b0b7213)
![{\displaystyle \mathbf {B} (\mathbf {r}) = {\frac {\mu _{0}}{4\pi }}\left[{\frac {3\mathbf {\hat {r}} (\mathbf {\hat {r}} \cdot \mathbf {m} )-\mathbf {m} }{|\mathbf {r} |^{3}}}+{\frac {8\pi }{3 }}\mathbf {m} \delta (\mathbf {r} )\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b47f91d20595386326b2945ac17533fd823321db)


















