Скорость звука
_-_filtered.jpg/440px-FA-18_Hornet_breaking_sound_barrier_(7_July_1999)_-_filtered.jpg)
| Звуковые измерения | |
|---|---|
Характеристика | Символы |
| Звуковое давление | п , SPL, L PA |
| Скорость частиц | в , СВЛ |
| Смещение частиц | δ |
| Интенсивность звука | Я , СИЛ |
| Мощность звука | П , SWL, L WA |
| Звуковая энергия | Вт |
| Плотность звуковой энергии | ж |
| Звуковое воздействие | Э , СЕЛ |
| Акустическое сопротивление | З |
| Звуковая частота | АФ |
| Потеря передачи | ТЛ |
Скорость звука — это расстояние, проходимое звуковой волной за единицу времени при ее распространении через упругую среду. Проще говоря, скорость звука — это скорость распространения колебаний. При температуре 20 °C (68 °F) скорость звука в воздухе составляет около 343 м/с (1125 фут/с ; 1235 км/ч ; 767 миль/ч ; 667 узлов ), или1 км в2,91 с или одна миля за4,69 с . Она сильно зависит от температуры, а также от среды, через которую распространяется звуковая волна . При 0 °C (32 °F) скорость звука в воздухе составляет около 331 м/с (1086 футов/с; 1192 км/ч; 740 миль/ч; 643 узла). [1]
Скорость звука в идеальном газе зависит только от его температуры и состава. Скорость слабо зависит от частоты и давления в обычном воздухе, немного отклоняясь от идеального поведения. В разговорной речи скорость звука относится к скорости звуковых волн в воздухе . Однако скорость звука варьируется от вещества к веществу: как правило, звук распространяется медленнее всего в газах , быстрее в жидкостях и быстрее всего в твердых телах . Например, в то время как звук распространяется со скоростью343 м/с в воздухе, он движется со скоростью1481 м/с в воде (почти в 4,3 раза быстрее) и при5120 м/с в железе (почти в 15 раз быстрее). В исключительно жестком материале, таком как алмаз, звук распространяется со скоростью 12 000 м/с (39 370 футов/с), [2] — примерно в 35 раз больше его скорости в воздухе и примерно с максимальной скоростью, с которой он может распространяться при нормальных условиях. Теоретически скорость звука на самом деле является скоростью колебаний. Звуковые волны в твердых телах состоят из волн сжатия (как в газах и жидкостях) и другого типа звуковой волны, называемой сдвиговой волной , которая встречается только в твердых телах. Сдвиговые волны в твердых телах обычно распространяются с другой скоростью, чем волны сжатия, как показано в сейсмологии . Скорость волн сжатия в твердых телах определяется сжимаемостью среды , модулем сдвига и плотностью. Скорость сдвиговых волн определяется только модулем сдвига и плотностью твердого материала.
В гидродинамике скорость звука в текучей среде (газе или жидкости) используется как относительная мера скорости объекта, движущегося через среду. Отношение скорости объекта к скорости звука (в той же среде) называется числом Маха объекта . Объекты, движущиеся со скоростью, большей скорости звука ( число Маха 1 ), называются движущимися со сверхзвуковой скоростью.
Земля
В атмосфере Земли скорость звука сильно варьируется: от примерно 295 м/с (1060 км/ч; 660 миль/ч) на больших высотах до примерно 355 м/с (1280 км/ч; 790 миль/ч) при высоких температурах.
История
В «Началах» сэра Исаака Ньютона 1687 года содержится расчет скорости звука в воздухе, которая составляет 979 футов в секунду (298 м/с). Это значение занижено примерно на 15%. [3] Расхождение в первую очередь обусловлено пренебрежением (тогда неизвестным) эффектом быстро меняющейся температуры в звуковой волне (говоря современным языком, сжатие и расширение воздуха звуковой волной — это адиабатический , а не изотермический процесс ). Эта ошибка была позже исправлена Лапласом . [4]
В 17 веке было предпринято несколько попыток точно измерить скорость звука, включая попытки Марина Мерсенна в 1630 году (1380 парижских футов в секунду), Пьера Гассенди в 1635 году (1473 парижских фута в секунду) и Роберта Бойля (1125 парижских футов в секунду). [5] В 1709 году преподобный Уильям Дерхэм , ректор Апминстера, опубликовал более точное измерение скорости звука — 1072 парижских фута в секунду. [5] ( Парижский фут был325 мм . Это больше, чем стандартный «международный фут», который сегодня широко используется и который был официально определен в 1959 году как304,8 мм , что соответствует скорости звука при 20 °C (68 °F) 1055 парижских футов в секунду).
Дерхэм использовал телескоп с башни церкви Св. Лаврентия в Апминстере, чтобы наблюдать вспышку выстрела далекого ружья, а затем измерил время до того момента, как услышал выстрел, с помощью полусекундного маятника. Измерения производились по выстрелам из ряда местных достопримечательностей, включая церковь Норт-Окендон . Расстояние было известно с помощью триангуляции , и таким образом была рассчитана скорость, с которой распространялся звук. [6]
Основные понятия
Передачу звука можно проиллюстрировать с помощью модели, состоящей из ряда сферических объектов, соединенных между собой пружинами.
В реальных материальных терминах сферы представляют молекулы материала, а пружины представляют связи между ними. Звук проходит через систему, сжимая и расширяя пружины, передавая акустическую энергию соседним сферам. Это помогает передавать энергию в свою очередь пружинам (связям) соседней сферы и так далее.
Скорость звука через модель зависит от жесткости пружин и массы сфер. Пока расстояние между сферами остается постоянным, более жесткие пружины/связи передают энергию быстрее, в то время как более массивные сферы передают энергию медленнее .
В реальном материале жесткость пружин известна как « модуль упругости », а масса соответствует плотности материала . Звук будет распространяться медленнее в губчатых материалах и быстрее в более жестких. Такие эффекты, как дисперсия и отражение, также можно понять с помощью этой модели. [ необходима цитата ]
В некоторых учебниках ошибочно утверждается, что скорость звука увеличивается с плотностью. Это представление иллюстрируется представлением данных для трех материалов, таких как воздух, вода и сталь, и указанием, что скорость звука выше в более плотных материалах. Но в этом примере не учитывается, что материалы имеют сильно разную сжимаемость, что более чем компенсирует разницу в плотности, которая замедлила бы скорость волн в более плотных материалах. Наглядным примером двух эффектов является то, что звук распространяется всего в 4,3 раза быстрее в воде, чем в воздухе, несмотря на огромную разницу в сжимаемости двух сред. Причина в том, что большая плотность воды, которая замедляет звук в воде по сравнению с воздухом, почти компенсирует разницу в сжимаемости двух сред.
Например, звук будет распространяться в 1,59 раза быстрее в никеле, чем в бронзе, из-за большей жесткости никеля при примерно той же плотности. Аналогично, звук распространяется примерно в 1,41 раза быстрее в легком водороде ( протии ), чем в тяжелом водороде ( дейтерии ), поскольку дейтерий имеет схожие свойства, но в два раза большую плотность. В то же время звук «компрессионного типа» будет распространяться быстрее в твердых телах, чем в жидкостях, и быстрее в жидкостях, чем в газах, потому что твердые тела труднее сжимать, чем жидкости, а жидкости, в свою очередь, труднее сжимать, чем газы.
Практический пример можно наблюдать в Эдинбурге, когда "One o'Clock Gun" стреляет в восточной части Эдинбургского замка. Стоя у основания западной части Замковой скалы, звук выстрела Пушки можно услышать через скалу, немного раньше, чем он прибудет по воздуху, частично задержанный немного более длинным путем. Это особенно эффективно, если стреляют из нескольких орудий, например, в "The Queen's Birthday".
Волны сжатия и сдвига


В газе или жидкости звук состоит из волн сжатия. В твердых телах волны распространяются как два разных типа. Продольная волна связана с сжатием и декомпрессией в направлении движения и является тем же процессом в газах и жидкостях, с аналогичной волной типа сжатия в твердых телах. Только волны сжатия поддерживаются в газах и жидкостях. Дополнительный тип волны, поперечная волна , также называемая сдвиговой волной , возникает только в твердых телах, поскольку только твердые тела поддерживают упругие деформации. Она возникает из-за упругой деформации среды, перпендикулярной направлению движения волны; направление сдвиговой деформации называется « поляризацией » этого типа волны. В общем случае поперечные волны возникают как пара ортогональных поляризаций.
Эти разные волны (волны сжатия и различные поляризации сдвиговых волн) могут иметь разные скорости на одной и той же частоте. Поэтому они достигают наблюдателя в разное время, экстремальным примером является землетрясение , когда сначала приходят резкие волны сжатия, а через несколько секунд — качающиеся поперечные волны.
Скорость волны сжатия в жидкости определяется сжимаемостью и плотностью среды . В твердых телах волны сжатия аналогичны волнам в жидкостях, зависящим от сжимаемости и плотности, но с дополнительным фактором модуля сдвига , который влияет на волны сжатия из-за внеосевых упругих энергий, которые способны влиять на эффективное растяжение и релаксацию при сжатии. Скорость волн сдвига, которые могут возникать только в твердых телах, определяется просто модулем сдвига и плотностью твердого материала.
Уравнения
Скорость звука в математической нотации традиционно обозначается буквой c , от латинского celeritas, что означает «быстрота».
Для жидкостей в целом скорость звука c определяется уравнением Ньютона-Лапласа: где
- - коэффициент жесткости, изоэнтропический модуль объемной упругости (или модуль объемной упругости для газов);
- это плотность .
, где — давление, а производная берется изоэнтропически, то есть при постоянной энтропии s . Это происходит потому, что звуковая волна распространяется так быстро, что ее распространение можно аппроксимировать как адиабатический процесс , что означает, что в течение цикла давления звука недостаточно времени для существенной теплопроводности и излучения.
Таким образом, скорость звука увеличивается с увеличением жесткости (сопротивления упругого тела деформации под действием приложенной силы) материала и уменьшается с увеличением плотности. Для идеальных газов объемный модуль упругости K — это просто давление газа, умноженное на безразмерный показатель адиабаты , который для воздуха при нормальных условиях давления и температуры составляет около 1,4.
Для общих уравнений состояния , если использовать классическую механику , скорость звука c можно вывести [7] следующим образом:
Рассмотрим звуковую волну, распространяющуюся со скоростью по трубе, выровненной с осью и имеющей площадь поперечного сечения . За промежуток времени она проходит длину . В установившемся состоянии массовый расход должен быть одинаковым на обоих концах трубы, поэтому массовый поток постоянен и . Согласно второму закону Ньютона , сила градиента давления обеспечивает ускорение:
И поэтому:
Если релятивистские эффекты важны, скорость звука рассчитывается из релятивистских уравнений Эйлера .
В недисперсионной среде скорость звука не зависит от частоты звука , поэтому скорости переноса энергии и распространения звука одинаковы для всех частот. Воздух, смесь кислорода и азота, представляет собой недисперсионную среду. Однако воздух содержит небольшое количество CO2 , который является дисперсионной средой и вызывает дисперсию в воздухе на ультразвуковых частотах (выше28 кГц ). [8]
В дисперсионной среде скорость звука является функцией частоты звука через дисперсионное соотношение . Каждая частотная компонента распространяется со своей собственной скоростью, называемой фазовой скоростью , в то время как энергия возмущения распространяется с групповой скоростью . То же самое явление происходит со световыми волнами; см. оптическую дисперсию для описания.
Зависимость от свойств среды
Скорость звука является переменной величиной и зависит от свойств вещества, через которое распространяется волна. В твердых телах скорость поперечных (или сдвиговых) волн зависит от деформации сдвига под действием касательного напряжения (называемой модулем сдвига ) и плотности среды. Продольные (или компрессионные) волны в твердых телах зависят от тех же двух факторов с добавлением зависимости от сжимаемости .
В жидкостях только сжимаемость и плотность среды являются важными факторами, поскольку жидкости не передают касательные напряжения. В неоднородных жидкостях, таких как жидкость, заполненная пузырьками газа, плотность жидкости и сжимаемость газа влияют на скорость звука аддитивным образом, как показано в эффекте горячего шоколада .
В газах адиабатическая сжимаемость напрямую связана с давлением через коэффициент теплоемкости (показатель адиабаты), тогда как давление и плотность обратно пропорциональны температуре и молекулярной массе, поэтому важны только совершенно независимые свойства температуры и молекулярной структуры (коэффициент теплоемкости может быть определен температурой и молекулярной структурой, но для его определения недостаточно простого молекулярного веса).
Звук распространяется быстрее в газах с низкой молекулярной массой , таких как гелий , чем в более тяжелых газах, таких как ксенон . Для одноатомных газов скорость звука составляет около 75% от средней скорости, с которой движутся атомы в этом газе.
Для заданного идеального газа молекулярный состав фиксирован, и, таким образом, скорость звука зависит только от его температуры . При постоянной температуре давление газа не влияет на скорость звука, поскольку плотность будет увеличиваться, и поскольку давление и плотность (также пропорциональны давлению) оказывают одинаковое, но противоположное влияние на скорость звука, и эти два вклада полностью компенсируются. Аналогичным образом, волны сжатия в твердых телах зависят как от сжимаемости, так и от плотности — как и в жидкостях — но в газах плотность вносит вклад в сжимаемость таким образом, что некоторая часть каждого атрибута выносится за скобки, оставляя только зависимость от температуры, молекулярного веса и отношения теплоемкости, которые можно независимо вывести из температуры и молекулярного состава (см. выводы ниже). Таким образом, для одного заданного газа (предполагая, что молекулярный вес не меняется) и в небольшом диапазоне температур (для которого теплоемкость относительно постоянна), скорость звука становится зависящей только от температуры газа.
В режиме неидеального поведения газа, для которого используется уравнение Ван-дер-Ваальса , пропорциональность не является точной, и существует небольшая зависимость скорости звука от давления газа.
Влажность оказывает небольшое, но измеримое влияние на скорость звука (увеличивая ее примерно на 0,1–0,6%), поскольку молекулы кислорода и азота воздуха заменяются более легкими молекулами воды . Это простой эффект смешивания.
Изменение высоты и его влияние на акустику атмосферы

В атмосфере Земли главным фактором, влияющим на скорость звука, является температура . Для заданного идеального газа с постоянной теплоемкостью и составом скорость звука зависит исключительно от температуры; см. § Подробности ниже. В таком идеальном случае эффекты уменьшения плотности и уменьшения давления высоты компенсируют друг друга, за исключением остаточного эффекта температуры.
Поскольку температура (и, следовательно, скорость звука) уменьшается с увеличением высоты до11 км звук преломляется вверх, в сторону от слушателей на земле, создавая акустическую тень на некотором расстоянии от источника. [9] Уменьшение скорости звука с высотой называется отрицательным градиентом скорости звука .
Однако выше имеются различия в этой тенденции.11 км . В частности, в стратосфере выше примерно20 км , скорость звука увеличивается с высотой из-за повышения температуры от нагрева внутри озонового слоя . Это создает положительный градиент скорости звука в этой области. Еще одна область положительного градиента возникает на очень больших высотах, в термосфере выше90 км .
Подробности
Скорость звука в идеальных газах и воздухе
Для идеального газа K ( модуль объемной упругости в уравнениях выше, эквивалентный C , коэффициенту жесткости в твердых телах) определяется по формуле Таким образом, из уравнения Ньютона-Лапласа выше, скорость звука в идеальном газе определяется по формуле, где
- γ — адиабатический показатель, также известный как изоэнтропический коэффициент расширения . Это отношение удельной теплоты газа при постоянном давлении к удельной теплоте газа при постоянном объеме ( ) и возникает из-за того, что классическая звуковая волна вызывает адиабатическое сжатие, при котором теплота сжатия не успевает выйти за пределы импульса давления, и, таким образом, вносит вклад в давление, вызванное сжатием;
- p — давление ;
- ρ — плотность .
Используя закон идеального газа, заменив p на nRT / V и заменив ρ на nM / V , уравнение идеального газа принимает вид , где
- c ideal — скорость звука в идеальном газе ;
- R — молярная газовая постоянная ;
- k — постоянная Больцмана ;
- γ (гамма) — показатель адиабаты . При комнатной температуре, когда тепловая энергия полностью распределяется на вращение (вращения полностью возбуждаются), но квантовые эффекты предотвращают возбуждение колебательных мод, значение составляет 7/5 = 1,400 для двухатомных газов (таких как кислород и азот ), согласно кинетической теории. Гамма фактически экспериментально измеряется в диапазоне от 1,3991 до 1,403 при0 °C для воздуха. Гамма составляет ровно 5/3 = 1,667 для одноатомных газов (таких как аргон ) и 4/3 = 1,333 для трехатомных молекулярных газов, таких как H
2O , не являются коллинеарными (коллинеарный трехатомный газ, такой как CO
2эквивалентен двухатомному газу для наших целей); - T — абсолютная температура;
- M — молярная масса газа. Средняя молярная масса для сухого воздуха составляет около 0,02897 кг/моль (28,97 г/моль);
- n — число молей;
- m — масса одной молекулы.
Это уравнение применимо только тогда, когда звуковая волна является небольшим возмущением состояния окружающей среды, и выполняются некоторые другие отмеченные условия, как указано ниже. Было обнаружено, что расчетные значения для c air немного отличаются от экспериментально определенных значений. [10]
Ньютон, как известно, рассматривал скорость звука до развития термодинамики и поэтому неправильно использовал изотермические расчеты вместо адиабатических . В его результате отсутствовал фактор γ , но в остальном он был верным.
Численная подстановка приведенных выше значений дает приближение идеального газа к скорости звука для газов, которое является точным при относительно низких давлениях и плотностях газа (для воздуха это включает стандартные условия на уровне моря на Земле). Кроме того, для двухатомных газов использование γ = 1,4000 требует, чтобы газ существовал в достаточно высоком температурном диапазоне, чтобы вращательная теплоемкость была полностью возбуждена (т. е. молекулярное вращение полностью использовалось как «раздел» или резервуар тепловой энергии); но в то же время температура должна быть достаточно низкой, чтобы молекулярные колебательные моды не вносили вклад в теплоемкость (т. е. незначительное тепло переходит в вибрацию, поскольку все колебательные квантовые моды выше минимальной энергетической моды имеют энергии, которые слишком высоки, чтобы быть заселенными значительным числом молекул при этой температуре). Для воздуха эти условия выполняются при комнатной температуре, а также при температурах значительно ниже комнатной (см. таблицы ниже). См. раздел о газах в удельной теплоемкости для более полного обсуждения этого явления.
Для воздуха мы вводим сокращение
Кроме того, перейдем к температуре по Цельсию θ = T −273,15 К , что полезно для расчета скорости воздуха в регионе вблизи0 °С (273 К ). Тогда для сухого воздуха,
Подставляя числовые значения и используя значение идеального двухатомного газа γ = 1,4000 , имеем
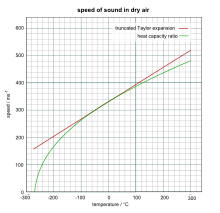
Наконец, разложение Тейлора оставшегося квадратного корня дает
График, сравнивающий результаты двух уравнений, показан справа, где для скорости звука использовано немного более точное значение 331,5 м/с (1088 футов/с).0 °С . [11] : 120-121
Эффекты, вызванные сдвигом ветра
Скорость звука меняется в зависимости от температуры. Поскольку температура и скорость звука обычно уменьшаются с увеличением высоты, звук преломляется вверх , от слушателей на земле, создавая акустическую тень на некотором расстоянии от источника. [9] Сдвиг ветра 4 м/(с · км) может вызвать преломление, равное типичному градиенту температуры7,5 °C/км . [12] Более высокие значения градиента ветра будут преломлять звук вниз к поверхности в направлении по ветру, [13] устраняя акустическую тень на подветренной стороне. Это увеличит слышимость звуков по ветру. Этот эффект преломления по ветру возникает из-за наличия градиента ветра; тот факт, что звук переносится ветром, не важен. [14]
Для распространения звука экспоненциальное изменение скорости ветра с высотой можно определить следующим образом: [15] где
- U ( h ) — скорость ветра на высоте h ;
- ζ — экспоненциальный коэффициент, основанный на шероховатости поверхности земли, обычно от 0,08 до 0,52;
- dU / dH ( h ) — ожидаемый градиент ветра на высоте h .
В битве при Иуке во время Гражданской войны в США в 1862 году акустическая тень, предположительно усиленная северо-восточным ветром, не позволила двум дивизиям солдат Союза принять участие в битве, [16] потому что они не могли слышать звуки битвы, а только10 км (шесть миль) по ветру. [17]
Таблицы
- Т 0 есть273,15 К (=0 °С =32 °F ), что дает теоретическое значение331,3 м/с (=1 086 .9 фут/с =1193 км/ч =741,1 миль/ч = 644,0 узлов ). Значения в диапазоне от 331,3 доОднако в справочной литературе можно найти значение 331,6 м/с ;
- Т 20 это293,15 К (=20 °С =68 °F ), что дает значение343,2 м/с (=1 126 .0 фут/с =1236 км/ч =767,8 миль/ч = 667,2 узлов );
- Т 25 это298,15 К (=25 °С =77 °F ), что дает значение346,1 м/с (=1 135 .6 фут/с =1246 км/ч =774,3 миль/ч = 672,8 узлов ).
Фактически, если предположить, что газ идеальный , скорость звука c зависит только от температуры и состава, а не от давления или плотности (поскольку они изменяются синхронно для данной температуры и взаимно уничтожаются). Воздух — почти идеальный газ. Температура воздуха меняется с высотой, что приводит к следующим изменениям скорости звука при использовании стандартной атмосферы — фактические условия могут отличаться . [ требуется ссылка ]
Температура Цельсия θ [ °C ] | Скорость звука с [ м / с ] | Плотность воздуха ρ [ кг / м 3 ] | Характеристическое удельное акустическое сопротивление z 0 [ Па ⋅ с / м ] |
|---|---|---|---|
| 35 | 351,88 | 1.1455 | 403.2 |
| 30 | 349.02 | 1.1644 | 406.5 |
| 25 | 346.13 | 1.1839 | 409.4 |
| 20 | 343.21 | 1.2041 | 413.3 |
| 15 | 340.27 | 1.2250 | 416.9 |
| 10 | 337.31 | 1.2466 | 420,5 |
| 5 | 334.32 | 1.2690 | 424.3 |
| 0 | 331.30 | 1.2922 | 428.0 |
| −5 | 328.25 | 1.3163 | 432.1 |
| −10 | 325.18 | 1.3413 | 436.1 |
| −15 | 322.07 | 1.3673 | 440.3 |
| −20 | 318.94 | 1.3943 | 444,6 |
| −25 | 315.77 | 1.4224 | 449.1 |
При нормальных атмосферных условиях температура, а следовательно, и скорость звука, изменяются с высотой:
| Высота | Температура | РС | км/ч | миль/ч | кн |
|---|---|---|---|---|---|
| Уровень моря | 15 °С (59 °F ) | 340 | 1,225 | 761 | 661 |
| 11 000–20 000 м (высота полета коммерческих самолетов и первый сверхзвуковой полет ) | −57 °С (−70 °F ) | 295 | 1,062 | 660 | 573 |
| 29 000 м (полет X-43A ) | −48 °С (−53 °F ) | 301 | 1,083 | 673 | 585 |
Влияние частоты и состава газа
Общие физические соображения
Среда, в которой распространяется звуковая волна, не всегда реагирует адиабатически, и в результате скорость звука может меняться в зависимости от частоты. [18]
Ограничения концепции скорости звука из-за экстремального затухания также вызывают беспокойство. Затухание, которое существует на уровне моря для высоких частот, применяется к последовательно более низким частотам по мере уменьшения атмосферного давления или увеличения средней длины свободного пробега . По этой причине концепция скорости звука (за исключением частот, приближающихся к нулю) постепенно теряет область применимости на больших высотах. [10] Стандартные уравнения для скорости звука применяются с разумной точностью только в ситуациях, в которых длина звуковой волны значительно больше средней длины свободного пробега молекул в газе.
Молекулярный состав газа вносит вклад как в массу (M) молекул, так и в их теплоемкость, и поэтому оба они влияют на скорость звука. В общем, при одинаковой молекулярной массе одноатомные газы имеют немного более высокую скорость звука (более чем на 9% выше), поскольку у них более высокий γ ( 5/3 = 1,66 ...), чем у двухатомных ( 7/5 = 1,4 ). Таким образом, при одинаковой молекулярной массе скорость звука одноатомного газа увеличивается в раз
Это дает разницу в 9% и будет типичным соотношением для скоростей звука при комнатной температуре в гелии и дейтерии , каждый с молекулярным весом 4. Звук распространяется быстрее в гелии, чем в дейтерии, потому что адиабатическое сжатие нагревает гелий больше, поскольку молекулы гелия могут сохранять тепловую энергию от сжатия только при поступательном движении, но не при вращении. Таким образом, молекулы гелия (одноатомные молекулы) движутся быстрее в звуковой волне и передают звук быстрее. (Звук распространяется примерно со скоростью 70% от средней молекулярной скорости в газах; этот показатель составляет 75% в одноатомных газах и 68% в двухатомных газах).
В этом примере мы предположили, что температура достаточно низкая, чтобы теплоемкости не подвергались влиянию молекулярных колебаний (см. теплоемкость ). Однако колебательные моды просто вызывают гаммы, которые уменьшаются к 1, поскольку колебательные моды в многоатомном газе дают газу дополнительные способы хранения тепла, которые не влияют на температуру, и, таким образом, не влияют на молекулярную скорость и скорость звука. Таким образом, эффект более высоких температур и колебательной теплоемкости приводит к увеличению разницы между скоростью звука в одноатомных и многоатомных молекулах, при этом скорость остается большей в одноатомных.
Практическое применение в воздухе
Безусловно, наиболее важным фактором, влияющим на скорость звука в воздухе, является температура. Скорость пропорциональна квадратному корню абсолютной температуры, что дает увеличение примерно на0,6 м/с на градус Цельсия. По этой причине высота звука духового музыкального инструмента увеличивается по мере повышения его температуры.
Скорость звука увеличивается из-за влажности. Разница между 0% и 100% влажности составляет около1,5 м/с при стандартном давлении и температуре, но величина эффекта влажности резко увеличивается с температурой.
Зависимость от частоты и давления обычно незначительна в практических приложениях. В сухом воздухе скорость звука увеличивается примерно на0,1 м/с по мере увеличения частоты от10 Гц до100 Гц . Для слышимых частот выше100 Гц она относительно постоянна. Стандартные значения скорости звука указаны в пределе низких частот, где длина волны велика по сравнению со средней длиной свободного пробега. [19]
Как показано выше, приблизительное значение 1000/3 = 333,33... м/с немного ниже, а точное значение5 °C и является хорошим приближением для всех «обычных» наружных температур (по крайней мере, в умеренном климате), отсюда обычное эмпирическое правило для определения того, как далеко ударила молния: посчитайте секунды от начала вспышки молнии до начала соответствующего раската грома и разделите на 3: результат — расстояние в километрах до ближайшей точки удара молнии. Или разделите количество секунд на 5 для приблизительного расстояния в милях.
число Маха
Число Маха, полезная величина в аэродинамике, представляет собой отношение скорости воздуха к локальной скорости звука. На высоте, по объясненным причинам, число Маха является функцией температуры. Однако приборы для полета самолета работают, используя перепад давления для вычисления числа Маха, а не температуры. Предполагается, что определенное давление представляет определенную высоту и, следовательно, стандартную температуру. Приборы для полета самолета должны работать таким образом, поскольку давление стагнации, определяемое трубкой Пито, зависит как от высоты, так и от скорости.
Экспериментальные методы
Существует ряд различных методов измерения звука в воздухе.
Самая ранняя достаточно точная оценка скорости звука в воздухе была сделана Уильямом Дерхэмом и признана Исааком Ньютоном . У Дерхэма был телескоп на вершине башни церкви Святого Лаврентия в Апминстере , Англия. В безветренный день синхронизированные карманные часы давали помощнику, который стрелял из ружья в заранее определенное время с заметной точки в нескольких милях от него, по всей сельской местности. Это можно было подтвердить с помощью телескопа. Затем он измерил интервал между появлением дыма и появлением звука с помощью полусекундного маятника. Расстояние от места выстрела было найдено с помощью триангуляции, а простое деление (расстояние/время) дало скорость. Наконец, сделав множество наблюдений, используя диапазон различных расстояний, неточность полусекундного маятника можно было усреднить, что дало ему окончательную оценку скорости звука. Современные секундомеры позволяют использовать этот метод на расстояниях всего 200–400 метров, и для этого не требуется ничего такого громкого, как дробовик.
Методы однократного измерения времени
Самая простая концепция — это измерение, выполненное с использованием двух микрофонов и быстрого записывающего устройства, такого как цифровой накопительный зонд. Этот метод использует следующую идею.
Если источник звука и два микрофона расположены на прямой линии, причем источник звука находится на одном конце, то можно измерить следующее:
- Расстояние между микрофонами ( x ), называемое базисом микрофона.
- Время прибытия между сигналами (задержка), достигающими разных микрофонов ( t ).
Тогда v = x / t .
Другие методы
В этих методах измерение времени заменено измерением обратной величины времени ( частоты ).
Трубка Кундта — пример эксперимента, который можно использовать для измерения скорости звука в небольшом объеме. Преимущество этого метода в том, что он позволяет измерять скорость звука в любом газе. Этот метод использует порошок, чтобы сделать узлы и пучности видимыми для человеческого глаза. Это пример компактной экспериментальной установки.
Камертон можно держать около устья длинной трубы , погруженной в бочку с водой . В этой системе трубу можно привести в резонанс, если длина воздушного столба в трубе равна (1 + 2 n ) λ /4 , где n — целое число. Поскольку пучность трубы на открытом конце находится немного снаружи устья трубы, лучше всего найти две или более точек резонанса, а затем измерить половину длины волны между ними.
В данном случае v = fλ .
Высокоточные измерения в воздухе
Влияние примесей может быть значительным при проведении высокоточных измерений. Химические осушители могут использоваться для осушения воздуха, но, в свою очередь, загрязняют образец. Воздух можно осушить криогенно, но это также приводит к удалению углекислого газа; поэтому многие высокоточные измерения проводятся с воздухом, свободным от углекислого газа, а не с естественным воздухом. Обзор 2002 года [20] показал, что измерение 1963 года, проведенное Смитом и Харлоу с использованием цилиндрического резонатора, дало «наиболее вероятное значение стандартной скорости звука на сегодняшний день». Эксперимент проводился с воздухом, из которого был удален углекислый газ, но затем результат был скорректирован с учетом этого эффекта, чтобы он был применим к реальному воздуху. Эксперименты проводились при30 °C, но с поправкой на температуру, чтобы сообщить о них при0 °C . Результат составил 331,45 ± 0,01 м/с для сухого воздуха при STP, для частот от93 Гц - 1500 Гц .
Негазообразные среды
Скорость звука в твердых телах
Трехмерные тела
В твердом теле существует ненулевая жесткость как для объемных деформаций, так и для сдвиговых деформаций. Следовательно, возможно генерировать звуковые волны с различными скоростями в зависимости от режима деформации. Звуковые волны, генерирующие объемные деформации (сжатие) и сдвиговые деформации (сдвиг), называются волнами давления (продольными волнами) и сдвиговыми волнами (поперечными волнами) соответственно. При землетрясениях соответствующие сейсмические волны называются P-волнами (первичными волнами) и S-волнами (вторичными волнами) соответственно. Скорости звука этих двух типов волн, распространяющихся в однородном трехмерном твердом теле, соответственно определяются как [11] , где
- K — модуль объемной упругости упругих материалов;
- G — модуль сдвига упругих материалов;
- E — модуль Юнга ;
- ρ — плотность;
- ν — коэффициент Пуассона .
Последняя величина не является независимой, так как E = 3K(1 − 2ν) . Скорость волн давления зависит как от давления, так и от сдвиговых свойств материала, тогда как скорость сдвиговых волн зависит только от сдвиговых свойств.
Обычно волны давления распространяются в материалах быстрее, чем волны сдвига, и при землетрясениях это является причиной того, что началу землетрясения часто предшествует быстрый толчок вверх-вниз, до прибытия волн, которые производят движение из стороны в сторону. Например, для типичного стального сплава K = 170 ГПа , G = 80 ГПа и p =7700 кг/м 3 , что дает скорость сжатия c solid,p 6000 м/с . [11] Это находится в разумном согласии с c solid,p , измеренной экспериментально и составляющей5930 м/с для (возможно, другого) типа стали. [21] Скорость сдвига c solid,s оценивается в 3200 м/с с использованием тех же чисел.
Скорость звука в полупроводниковых твердых телах может быть очень чувствительна к количеству электронной примеси в них. [22]
Одномерные твердые тела
Скорость звука для волн давления в жестких материалах, таких как металлы, иногда приводится для «длинных стержней» рассматриваемого материала, в которых скорость легче измерить. В стержнях, диаметр которых короче длины волны, скорость чистых волн давления может быть упрощена и задана следующим образом: [11] : 70 , где E — модуль Юнга . Это похоже на выражение для сдвиговых волн, за исключением того, что модуль Юнга заменяет модуль сдвига . Эта скорость звука для волн давления в длинных стержнях всегда будет немного меньше той же скорости в однородных трехмерных твердых телах, а соотношение скоростей в двух различных типах объектов зависит от коэффициента Пуассона для материала.
Скорость звука в жидкостях
В жидкости единственной ненулевой жесткостью является жесткость объемной деформации (жидкость не выдерживает сдвигающих сил).
Следовательно, скорость звука в жидкости определяется выражением , где K — модуль объемной упругости жидкости.
Вода
В пресной воде звук распространяется со скоростью около1481 м/с в20 °C (см. раздел Внешние ссылки ниже для онлайн-калькуляторов). [23] Подводный звук можно использовать в гидролокации , акустической связи и акустической океанографии .
Морская вода

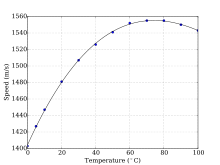
В соленой воде, свободной от пузырьков воздуха и взвешенных частиц, звук распространяется со скоростью около1500 м/с (1 500 .235 м/с при1000 килопаскалей ,10 °C и 3% солености по одному методу). [24] Скорость звука в морской воде зависит от давления (следовательно, глубины), температуры (изменение1 °С ~4 м/с ) и соленость (изменение на 1 ‰ ~1 м/с ), и были выведены эмпирические уравнения для точного расчета скорости звука из этих переменных. [25] [26] Другие факторы, влияющие на скорость звука, незначительны. Поскольку в большинстве регионов океана температура уменьшается с глубиной, профиль скорости звука с глубиной уменьшается до минимума на глубине в несколько сотен метров. Ниже минимума скорость звука снова увеличивается, поскольку эффект увеличения давления преодолевает эффект уменьшения температуры (справа). [27] Для получения дополнительной информации см. Dushaw et al. [28]
Эмпирическое уравнение для скорости звука в морской воде предоставлено Маккензи: [29] где
- T — температура в градусах Цельсия;
- S — соленость в частях на тысячу;
- z — глубина в метрах.
Константы a 1 , a 2 , ..., a 9 имеют контрольное значение1 550 .744 м/с для T =25 °C , S = 35 частей на тысячу , z = 1000 м . Это уравнение имеет стандартную ошибку0,070 м/с для солености от 25 до 40 ppt . Онлайн-калькулятор см. в [1].
(График зависимости скорости звука от глубины не коррелирует напрямую с формулой Маккензи. Это связано с тем, что температура и соленость меняются на разных глубинах. Когда T и S остаются постоянными, сама формула всегда увеличивается с глубиной.)
Другие уравнения для скорости звука в морской воде точны в широком диапазоне условий, но они гораздо сложнее, например, уравнение В. А. Дель Гроссо [30] и уравнение Чена-Миллеро-Ли. [28] [31]
Скорость звука в плазме
Скорость звука в плазме для общего случая, когда электроны горячее ионов (но не намного), определяется по формуле (см. здесь ) , где
- m i — масса иона ;
- μ — отношение массы иона к массе протона μ = mi / mp ;
- T e — температура электронов ;
- Z — зарядовое состояние;
- k — постоянная Больцмана ;
- γ — показатель адиабаты .
В отличие от газа, давление и плотность обеспечиваются отдельными видами: давление электронами, а плотность ионами. Они связаны через флуктуирующее электрическое поле.
Марс
Скорость звука на Марсе меняется в зависимости от частоты. Более высокие частоты распространяются быстрее, чем более низкие частоты. Высокочастотный звук от лазеров распространяется со скоростью 250 м/с (820 футов/с), в то время как низкочастотный звук достиг максимальной скорости 240 м/с (790 футов/с). [32]
Градиенты
Когда звук распространяется равномерно во всех направлениях в трех измерениях, интенсивность падает пропорционально обратному квадрату расстояния. Однако в океане есть слой, называемый «глубоким звуковым каналом» или каналом SOFAR , который может ограничивать звуковые волны на определенной глубине.
В канале SOFAR скорость звука ниже, чем в слоях выше и ниже. Так же, как световые волны будут преломляться в сторону области с более высоким показателем преломления , звуковые волны будут преломляться в сторону области, где их скорость уменьшается. Результатом является то, что звук ограничивается слоем, во многом так же, как свет может быть ограничен листом стекла или оптического волокна . Таким образом, звук ограничивается по существу в двух измерениях. В двух измерениях интенсивность падает пропорционально только обратной величине расстояния. Это позволяет волнам распространяться гораздо дальше, прежде чем они станут необнаружимо слабыми.
Похожий эффект происходит в атмосфере. Проект Mogul успешно использовал этот эффект для обнаружения ядерного взрыва на значительном расстоянии.
Смотрите также
- Акустоупругий эффект
- Упругая волна
- Второй звук
- Звуковой удар
- Звуковой барьер
- Скорости звука стихий
- Подводная акустика
- Вибрации
- Белл X-1
Ссылки
- ^ "Калькулятор скорости звука". Национальная метеорологическая служба . Получено 23 июля 2021 г.
- ^ "Скорость звука". hyperphysics.phy-astr.gsu.edu . Получено 24 октября 2022 г. .
- ^ "Скорость звука". mathpages.com . Получено 3 мая 2015 г. .
- ^ Бэннон, Майк; Капута, Фрэнк (12 декабря 2014 г.). «Уравнение Ньютона–Лапласа и скорость звука». Thermal Jackets . Получено 3 мая 2015 г. .
- ^ ab Murdin, Paul (25 декабря 2008 г.). Полный меридиан славы: опасные приключения в соревновании по измерению Земли . Springer Science & Business Media. стр. 35–36. ISBN 9780387755342.
- ^ Фокс, Тони (2003). Essex Journal . Essex Arch & Hist Soc. стр. 12–16.
- ^ "17.2 Скорость звука | Университетская физика Том 1". courses.lumenlearning.com . Получено 24 января 2020 г. .
- ^ Дин, Э.А. (август 1979 г.). Влияние атмосферы на скорость звука, Технический отчет Технического информационного центра Министерства обороны
- ^ ab Everest, F. (2001). Главный справочник по акустике . Нью-Йорк: McGraw-Hill. С. 262–263. ISBN 978-0-07-136097-5.
- ^ ab Стандартная атмосфера США, 1976, Типография правительства США, Вашингтон, округ Колумбия, 1976.
- ^ abcd Кинслер, LE; Фрей, AR; Коппенс, AB; Сандерс, JV (2000). Основы акустики (4-е изд.). Нью-Йорк: John Wiley & Sons. ISBN 0-471-84789-5.
- ^ Уман, Мартин (1984). Молния . Нью-Йорк: Dover Publications. ISBN 978-0-486-64575-9.
- ^ Volland, Hans (1995). Справочник по атмосферной электродинамике . Boca Raton: CRC Press. стр. 22. ISBN 978-0-8493-8647-3.
- ^ Сингал, С. (2005). Шумовое загрязнение и стратегия контроля . Оксфорд: Alpha Science International. стр. 7. ISBN 978-1-84265-237-4.
Можно заметить, что эффекты рефракции возникают только из-за градиента ветра, а не из-за конвекции звука под действием ветра.
- ^ Биес, Дэвид (2009). Инженерный контроль шума, теория и практика . Лондон: CRC Press. стр. 249. ISBN 978-0-415-26713-7Поскольку
скорость ветра обычно увеличивается с высотой, ветер, дующий от источника к слушателю, будет преломлять звуковые волны вниз, что приведет к повышению уровня шума.
- ^ Корнуолл, сэр (1996). Грант как военный командующий . Нью-Йорк: Barnes & Noble. стр. 92. ISBN 978-1-56619-913-1.
- ^ Козенс, Питер (2006). Самые темные дни войны: битвы при Иуке и Коринфе . Чапел-Хилл: Издательство Университета Северной Каролины. ISBN 978-0-8078-5783-0.
- ^ AB Wood , Учебник звука (Bell, Лондон, 1946)
- ^ "Скорость звука в воздухе". Phy.mtu.edu . Получено 13 июня 2014 г.
- ^ Цукервар, Справочник по скорости звука в реальных газах, стр. 52
- ^ J. Krautkramer и H. Krautkramer (1990), Ультразвуковой контроль материалов , 4-е полностью переработанное издание, Springer-Verlag, Берлин, Германия, стр. 497
- ^ Слэйд, Тайлер; Ананд, Шашват; Вуд, Макс; Мэйл, Джеймс; Имасато, Казуки; Шейх, Дин; Аль Малки, Муат; Агне, Маттиас; Гриффит, Кент; Букс, Сабах; Вулвертон, Крис; Канатзидис, Меркури; Снайдер, Джефф (2021). «Смягчение решетки, вызванное носителями заряда, способствует высокому zT в термоэлектрических полупроводниках». Джоуль . 5 (5): 1168-1182. Bibcode : 2021Джоуль...5.1168S. doi : 10.1016/j.joule.2021.03.009 . S2CID 233598665.
- ^ "Скорость звука в воде при температурах от 32 до 212 oF (0–100 oC) — имперские единицы и единицы СИ". The Engineering Toolbox .
- ^ Вонг, Джордж СК; Чжу, Ши-мин (1995). «Скорость звука в морской воде как функция солености, температуры и давления». Журнал Акустического общества Америки . 97 (3): 1732. Bibcode : 1995ASAJ...97.1732W. doi : 10.1121/1.413048.
- ^ APL-UW TR 9407 Справочник по высокочастотным акустическим моделям океанической среды, стр. I1-I2.
- ^ Робинсон, Стивен (22 сентября 2005 г.). «Технические руководства – Скорость звука в морской воде». Национальная физическая лаборатория . Архивировано из оригинала 29 апреля 2017 г. Получено 7 декабря 2016 г.
- ^ "How Fast Does Sound Travel?". Открытие звука в море . Университет Род-Айленда. Архивировано из оригинала 20 мая 2017 года . Получено 30 ноября 2010 года .
- ^ ab Dushaw, Brian D.; Worcester, PF; Cornuelle, BD; Howe, BM (1993). «Об уравнениях для скорости звука в морской воде». Журнал акустического общества Америки . 93 (1): 255–275. Bibcode : 1993ASAJ...93..255D. doi : 10.1121/1.405660.
- ^ Кеннет В., Маккензи (1981). «Обсуждение определений скорости звука в морской воде». Журнал Акустического общества Америки . 70 (3): 801–806. Bibcode : 1981ASAJ...70..801M. doi : 10.1121/1.386919.
- ^ Del Grosso, VA (1974). «Новое уравнение для скорости звука в природных водах (со сравнением с другими уравнениями)». Журнал Акустического общества Америки . 56 (4): 1084–1091. Bibcode : 1974ASAJ...56.1084D. doi : 10.1121/1.1903388 .
- ^ Мейнен, Кристофер С.; Уоттс, Д. Рэндольф (1997). «Еще одно доказательство того, что алгоритм скорости звука Дель Гроссо точнее алгоритма Чена и Миллеро». Журнал акустического общества Америки . 102 (4): 2058–2062. Bibcode : 1997ASAJ..102.2058M. doi : 10.1121/1.419655. S2CID 38144335.
- ^ Морис, С.; Чиде, Б.; Мердок, Н.; Лоренц, РД; Мимун, Д.; Вьенс, Р. К.; Стотт, А.; Якоб, Х.; Бертран, Т.; Монмессен, Ф.; Ланца, Н. Л.; Альварес-Лламас, К.; Энджел, СМ; Аунг, М.; Баларам, Дж. (1 апреля 2022 г.). «Запись марсианского звукового ландшафта на месте». Nature . 605 (7911): 653–658. Bibcode :2022Natur.605..653M. doi : 10.1038/s41586-022-04679-0 . ISSN 1476-4687. PMC 9132769 . PMID 35364602.
Внешние ссылки
- Калькулятор скорости звука
- Расчет: скорость звука в воздухе и температура
- Скорость звука: важна температура, а не давление воздуха
- Свойства стандартной атмосферы США 1976 г.
- Скорость звука
- Как измерить скорость звука в лаборатории
- Звук когда-то распространялся со скоростью света?
- Акустические свойства различных материалов, включая скорость звука. Архивировано 16 февраля 2014 г. на Wayback Machine
- Открытие звука в море (использование звука людьми и другими животными)













![{\displaystyle {\begin{align}{\frac {dv}{dt}}&=-{\frac {1}{\rho }}{\frac {dP}{dx}}\\[1ex]\rightarrow dP&=(-\rho \,dv){\frac {dx}{dt}}=(v\,d\rho )v\\[1ex]\rightarrow v^{2}&\equiv c^{2}={\frac {dP}{d\rho }}\end{align}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d00b195aeca690b20dd277cf48ac3cc893505d37)




















