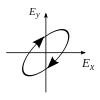Поляризация (волны)

Поляризация (также поляризация ) — это свойствопоперечных волн, которое определяет геометрическую ориентацию колебаний.[1][2][3][4][5] В поперечной волне направление колебания перпендикулярно направлению движения волны.[4] Простым примером поляризованной поперечной волны являются колебания, распространяющиеся вдоль натянутой струны(см. изображение), например, в музыкальном инструменте, таком какгитарная струна. В зависимости от того, как щипнута струна, колебания могут быть в вертикальном направлении, горизонтальном направлении или под любым углом, перпендикулярным струне. Напротив, впродольных волнах, таких какзвуковые волныв жидкости или газе, смещение частиц при колебании всегда происходит в направлении распространения, поэтому эти волны не демонстрируют поляризацию. Поперечные волны, которые демонстрируют поляризацию, включаютэлектромагнитные волны,такие каксветовыеирадиоволны,гравитационные волны,[6]и поперечные звуковые волны (сдвиговые волны) в твердых телах.
Электромагнитная волна, такая как свет, состоит из связанных колеблющихся электрического и магнитного полей , которые всегда перпендикулярны друг другу; по соглашению, «поляризация» электромагнитных волн относится к направлению электрического поля. При линейной поляризации поля колеблются в одном направлении. При круговой или эллиптической поляризации поля вращаются с постоянной скоростью в плоскости по мере распространения волны, либо в правом , либо в левом направлении.
Свет или другое электромагнитное излучение от многих источников, таких как солнце, пламя и лампы накаливания , состоит из коротких волновых последовательностей с равной смесью поляризаций; это называется неполяризованным светом . Поляризованный свет может быть получен путем пропускания неполяризованного света через поляризатор , который позволяет проходить волнам только одной поляризации. Наиболее распространенные оптические материалы не влияют на поляризацию света, но некоторые материалы — те, которые проявляют двойное лучепреломление , дихроизм или оптическую активность — влияют на свет по-разному в зависимости от его поляризации. Некоторые из них используются для изготовления поляризационных фильтров. Свет также становится частично поляризованным, когда он отражается под углом от поверхности.
Согласно квантовой механике , электромагнитные волны также можно рассматривать как потоки частиц, называемых фотонами . При таком рассмотрении поляризация электромагнитной волны определяется квантово-механическим свойством фотонов, называемым их спином . [7] [8] Фотон имеет один из двух возможных спинов: он может вращаться либо в правом , либо в левом направлении относительно своего направления движения. Циркулярно поляризованные электромагнитные волны состоят из фотонов только с одним типом спина, либо правым, либо левым. Линейно поляризованные волны состоят из фотонов, которые находятся в суперпозиции право- и левополяризованных циркулярно поляризованных состояний с одинаковой амплитудой и фазами, синхронизированными для создания колебаний в плоскости. [8]
Поляризация является важным параметром в областях науки, связанных с поперечными волнами, таких как оптика , сейсмология , радио и микроволны . Особенно сильное влияние оказывают такие технологии, как лазеры , беспроводные и оптоволоконные телекоммуникации и радары .
Введение
Распространение волн и поляризация
Большинство источников света классифицируются как некогерентные и неполяризованные (или только «частично поляризованные»), поскольку они состоят из случайной смеси волн, имеющих различные пространственные характеристики, частоты (длины волн), фазы и состояния поляризации. Однако для понимания электромагнитных волн и поляризации в частности проще просто рассмотреть когерентные плоские волны ; это синусоидальные волны одного конкретного направления (или волнового вектора ), частоты, фазы и состояния поляризации. Характеристика оптической системы по отношению к плоской волне с этими заданными параметрами затем может быть использована для предсказания ее реакции на более общий случай, поскольку волна с любой заданной пространственной структурой может быть разложена на комбинацию плоских волн (ее так называемый угловой спектр ). Некогерентные состояния могут быть смоделированы стохастически как взвешенная комбинация таких некоррелированных волн с некоторым распределением частот (ее спектром ), фазами и поляризациями.
Поперечные электромагнитные волны
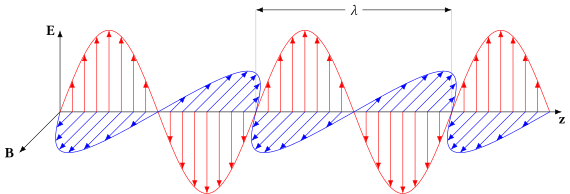
Электромагнитные волны (например, свет), распространяющиеся в свободном пространстве или другой однородной изотропной незатухающей среде, правильно описываются как поперечные волны , что означает, что вектор электрического поля плоской волны E и магнитное поле H находятся в некотором направлении, перпендикулярном (или «поперечном» к) направлению распространения волны; E и H также перпендикулярны друг другу. По соглашению, направление «поляризации» электромагнитной волны задается ее вектором электрического поля. Рассматривая монохроматическую плоскую волну оптической частоты f (свет вакуумной длины волны λ имеет частоту f = c/λ , где c — скорость света), давайте примем направление распространения за ось z . Будучи поперечной волной, поля E и H должны содержать компоненты только в направлениях x и y, тогда как E z = H z = 0. Используя комплексную (или векторную ) запись, мгновенные физические электрические и магнитные поля задаются действительными частями комплексных величин, встречающихся в следующих уравнениях. Как функция времени t и пространственного положения z (поскольку для плоской волны в направлении + z поля не зависят от x или y ) эти комплексные поля можно записать как: и где λ = λ 0 / n - длина волны в среде ( показатель преломления которой равен n ), а T = 1 / f - период волны. Здесь e x , ey , h x и h y - комплексные числа. Во второй, более компактной форме, как эти уравнения обычно выражаются, эти факторы описываются с помощью волнового числа k = 2π n / λ 0 и угловой частоты (или "радианной частоты") ω = 2π f . В более общей формулировке с распространением, не ограниченным +z направление, то пространственная зависимость kz заменяется на k → ∙ r → , где k → называется волновым вектором , величина которого является волновым числом.
Таким образом, ведущие векторы e и h содержат до двух ненулевых (комплексных) компонент, описывающих амплитуду и фазу x- и y -компонент поляризации волны (опять же, не может быть z -компоненты поляризации для поперечной волны в направлении + z ). Для заданной среды с характеристическим импедансом η , h связана с e следующим образом:
В диэлектрике η является действительным и имеет значение η 0 / n , где n — показатель преломления, а η 0 — импеданс свободного пространства . В проводящей среде импеданс будет комплексным. Обратите внимание, что, учитывая это соотношение, скалярное произведение E и H должно быть равно нулю: указывая на то, что эти векторы ортогональны (под прямым углом друг к другу), как и ожидалось.
Зная направление распространения ( в данном случае + z ) и η , можно точно так же задать волну в терминах просто e x и e y, описывающих электрическое поле. Вектор, содержащий e x и e y (но без компонента z , который обязательно равен нулю для поперечной волны), известен как вектор Джонса . Помимо указания состояния поляризации волны, общий вектор Джонса также определяет общую величину и фазу этой волны. В частности, интенсивность световой волны пропорциональна сумме квадратов величин двух компонентов электрического поля:
Однако состояние поляризации волны зависит только от (комплексного) отношения ey к e x . Поэтому давайте просто рассмотрим волны, у которых | e x | 2 + | ey | 2 = 1 ; это соответствует интенсивности около0,001 33 Вт /м2 в свободном пространстве (где η = η 0 ). И поскольку абсолютная фаза волны не важна при обсуждении ее состояния поляризации, давайте условимся, что фаза e x равна нулю; другими словами, e x является действительным числом, в то время как e y может быть комплексным. При этих ограничениях e x и e y можно представить следующим образом: где состояние поляризации теперь полностью параметризовано значением Q (таким, что −1 < Q < 1 ) и относительной фазой ϕ .
Непоперечные волны
Помимо поперечных волн, существует множество волновых движений, где колебания не ограничиваются направлениями, перпендикулярными направлению распространения. Эти случаи выходят далеко за рамки настоящей статьи, которая сосредоточена на поперечных волнах (таких как большинство электромагнитных волн в объемных средах), но следует знать о случаях, когда поляризация когерентной волны не может быть описана просто с помощью вектора Джонса, как мы только что сделали.
Только рассматривая электромагнитные волны, мы отмечаем, что предыдущее обсуждение строго применимо к плоским волнам в однородной изотропной незатухающей среде, тогда как в анизотропной среде (такой как двулучепреломляющие кристаллы, как обсуждается ниже) электрическое или магнитное поле может иметь как продольные, так и поперечные компоненты. В этих случаях электрическое смещение D и плотность магнитного потока B [ необходимо разъяснение ] по-прежнему подчиняются вышеуказанной геометрии, но из-за анизотропии в электрической восприимчивости (или в магнитной проницаемости ), теперь заданной тензором , направление E (или H ) может отличаться от направления D (или B ). Даже в изотропных средах так называемые неоднородные волны могут быть запущены в среду, показатель преломления которой имеет значительную мнимую часть (или « коэффициент экстинкции »), такую как металлы; [ необходимо разъяснение ] эти поля также не являются строго поперечными. [9] : 179–184 [10] : 51–52 Поверхностные волны или волны, распространяющиеся в волноводе (например, оптическом волокне ), как правило, не являются поперечными волнами, но могут быть описаны как электрическая или магнитная поперечная мода или гибридная мода.
Даже в свободном пространстве продольные компоненты поля могут генерироваться в фокальных областях, где приближение плоской волны нарушается. Крайним примером является радиально или тангенциально поляризованный свет, в фокусе которого электрическое или магнитное поле соответственно полностью продольное (вдоль направления распространения). [11]
Для продольных волн, таких как звуковые волны в жидкостях , направление колебаний по определению совпадает с направлением движения, поэтому вопрос поляризации обычно даже не упоминается. С другой стороны, звуковые волны в объемном твердом теле могут быть как поперечными, так и продольными, в общей сложности для трех компонентов поляризации. В этом случае поперечная поляризация связана с направлением касательного напряжения и смещения в направлениях, перпендикулярных направлению распространения, в то время как продольная поляризация описывает сжатие твердого тела и вибрацию вдоль направления распространения. Дифференциальное распространение поперечной и продольной поляризации важно в сейсмологии .
Состояние поляризации

Поляризация может быть определена в терминах чистых состояний поляризации только с когерентной синусоидальной волной на одной оптической частоте. Вектор на соседней диаграмме может описывать колебания электрического поля, испускаемого одномодовым лазером (частота колебаний которого обычно будет10 15 раз быстрее). Поле колеблется в плоскости xy вдоль страницы, при этом волна распространяется в направлении z , перпендикулярном странице. Первые две диаграммы ниже отображают вектор электрического поля в течение полного цикла для линейной поляризации в двух различных ориентациях; каждая из них считается отдельным состоянием поляризации (SOP). Линейную поляризацию под углом 45° можно также рассматривать как сложение горизонтально линейно поляризованной волны (как на крайнем левом рисунке) и вертикально поляризованной волны той же амплитуды в той же фазе .
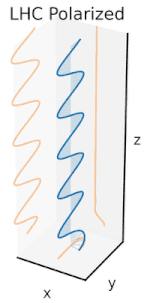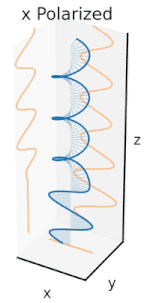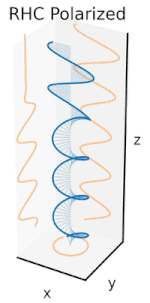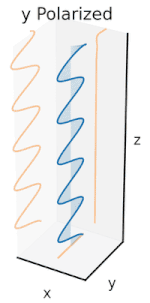
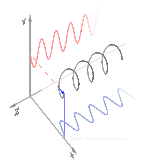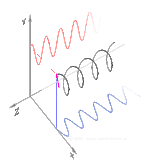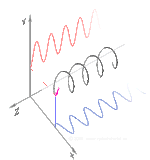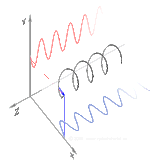
Теперь, если ввести сдвиг фаз между этими горизонтальными и вертикальными компонентами поляризации, то, как правило, получится эллиптическая поляризация [12], как показано на третьем рисунке. Когда сдвиг фаз составляет точно ±90°, а амплитуды одинаковы, то создается круговая поляризация (четвертый и пятый рисунки). Круговая поляризация может быть создана путем направления линейно поляризованного света через четвертьволновую пластину, ориентированную под углом 45° к линейной поляризации, чтобы создать два компонента одинаковой амплитуды с требуемым сдвигом фаз. Суперпозиция исходных и сдвинутых по фазе компонентов вызывает вращающийся вектор электрического поля, который изображен на анимации справа. Обратите внимание, что круговая или эллиптическая поляризация может включать в себя вращение поля как по часовой стрелке, так и против часовой стрелки, в зависимости от относительных фаз компонентов. Они соответствуют различным состояниям поляризации, таким как две круговые поляризации, показанные выше.
Ориентация осей x и y , используемая в этом описании, произвольна. Выбор такой системы координат и рассмотрение эллипса поляризации в терминах компонент поляризации x и y соответствует определению вектора Джонса (ниже) в терминах этих базисных поляризаций. Оси выбираются в соответствии с конкретной задачей, например, x находится в плоскости падения. Поскольку существуют отдельные коэффициенты отражения для линейных поляризаций в плоскости падения и ортогональных ей ( p и s поляризации, см. ниже), этот выбор значительно упрощает расчет отражения волны от поверхности.
Любая пара ортогональных поляризационных состояний может быть использована в качестве базисных функций, а не только линейные поляризации. Например, выбор правой и левой круговой поляризации в качестве базисных функций упрощает решение задач, связанных с круговым двулучепреломлением (оптической активностью) или круговым дихроизмом.
Эллипс поляризации

Для чисто поляризованной монохроматической волны вектор электрического поля за один цикл колебаний вычерчивает эллипс. Затем состояние поляризации можно описать в отношении геометрических параметров эллипса и его «рукопожатности», то есть, является ли вращение вокруг эллипса по часовой стрелке или против часовой стрелки. Одна параметризация эллиптической фигуры определяет угол ориентации ψ , определяемый как угол между большой осью эллипса и осью x [13] вместе с эллиптичностью ε = a/b , отношением большой оси эллипса к малой. [14] [15] [16] (также известной как осевое отношение ). Параметр эллиптичности является альтернативной параметризацией эксцентриситета эллипса или угла эллиптичности , как показано на рисунке. [13] Угол χ также важен, поскольку широта (угол от экватора) состояния поляризации, представленного на сфере Пуанкаре (см. ниже), равна ±2 χ . Частные случаи линейной и круговой поляризации соответствуют эллиптичности ε, равной бесконечности и единице (или χ, равной нулю и 45°) соответственно.
вектор Джонса
Полную информацию о полностью поляризованном состоянии также предоставляют амплитуда и фаза колебаний в двух компонентах вектора электрического поля в плоскости поляризации. Это представление было использовано выше, чтобы показать, как возможны различные состояния поляризации. Информацию об амплитуде и фазе удобно представить в виде двумерного комплексного вектора ( вектора Джонса ):
Здесь a 1 и a 2 обозначают амплитуду волны в двух компонентах вектора электрического поля, в то время как θ 1 и θ 2 представляют фазы. Произведение вектора Джонса с комплексным числом единичного модуля дает другой вектор Джонса, представляющий тот же эллипс и, следовательно, то же состояние поляризации. Физическое электрическое поле, как действительная часть вектора Джонса, будет изменено, но само состояние поляризации не зависит от абсолютной фазы . Базисные векторы, используемые для представления вектора Джонса, не обязательно должны представлять линейные состояния поляризации (т. е. быть действительными ). В общем случае можно использовать любые два ортогональных состояния, где ортогональная векторная пара формально определяется как имеющая нулевое внутреннее произведение . Обычным выбором являются левая и правая круговые поляризации, например, для моделирования различного распространения волн в двух таких компонентах в циркулярно двулучепреломляющих средах (см. ниже) или сигнальных трактов когерентных детекторов, чувствительных к круговой поляризации.
Координатная система
Независимо от того, представлено ли состояние поляризации с помощью геометрических параметров или векторов Джонса, в параметризации подразумевается ориентация системы координат. Это допускает степень свободы, а именно вращение вокруг направления распространения. При рассмотрении света, распространяющегося параллельно поверхности Земли, часто используются термины «горизонтальная» и «вертикальная» поляризация, причем первая связана с первым компонентом вектора Джонса или нулевым азимутальным углом. С другой стороны, в астрономии вместо этого обычно используется экваториальная система координат , при этом нулевой азимут (или позиционный угол, как его чаще называют в астрономии, чтобы избежать путаницы с горизонтальной системой координат ) соответствует точному северу.
сипобозначения
Другая часто используемая система координат относится к плоскости падения . Это плоскость, образованная направлением входящего распространения и вектором, перпендикулярным плоскости интерфейса, другими словами, плоскость, в которой луч движется до и после отражения или преломления. Компонент электрического поля, параллельный этой плоскости, называется p-подобным (параллельным), а компонент, перпендикулярный этой плоскости, называется s-подобным (от senkrecht , немецкого слова, означающего «перпендикулярный»). Поляризованный свет с его электрическим полем вдоль плоскости падения, таким образом, обозначается как p-поляризованный , в то время как свет, электрическое поле которого перпендикулярно плоскости падения, называется s-поляризованным . P -поляризация обычно называется поперечно-магнитной (TM), а также называется пи-поляризованной или π -поляризованной , или тангенциально-плоскостно-поляризованной . S -поляризация также называется поперечно-электрической (TE), а также сигма-поляризованной или σ-поляризованной , или сагиттально-плоскостно-поляризованной .
Степень поляризации
Степень поляризации ( DOP ) — это величина, используемая для описания части электромагнитной волны , которая поляризована. DOP можно рассчитать из параметров Стокса . Идеально поляризованная волна имеет DOP 100%, тогда как неполяризованная волна имеет DOP 0%. Волна, которая частично поляризована и, следовательно, может быть представлена суперпозицией поляризованного и неполяризованного компонента, будет иметь DOP где-то между 0 и 100%. DOP рассчитывается как доля полной мощности, переносимая поляризованным компонентом волны.
DOP может быть использован для отображения поля деформации в материалах при рассмотрении DOP фотолюминесценции . Поляризация фотолюминесценции связана с деформацией в материале посредством тензора фотоупругости данного материала .
DOP также визуализируется с помощью представления сферы Пуанкаре поляризованного пучка. В этом представлении DOP равен длине вектора, измеренного от центра сферы.
Неполяризованный и частично поляризованный свет
Неполяризованный свет — это свет со случайной, изменяющейся во времени поляризацией . Естественный свет, как и большинство других распространенных источников видимого света, производится независимо большим количеством атомов или молекул, чьи излучения некоррелированы .
Неполяризованный свет может быть получен из некогерентной комбинации вертикально и горизонтально линейно поляризованного света или право- и левополяризованного кругового света. [17] И наоборот, два составляющих линейно поляризованных состояния неполяризованного света не могут образовать интерференционную картину , даже если повернуты в выравнивание ( третий закон Френеля-Араго ). [18]
Так называемый деполяризатор действует на поляризованный луч, чтобы создать тот, в котором поляризация меняется так быстро по лучу, что это может быть проигнорировано в предполагаемых приложениях. И наоборот, поляризатор действует на неполяризованный луч или произвольно поляризованный луч, чтобы создать тот, который поляризован.
Неполяризованный свет можно описать как смесь двух независимых противоположно поляризованных потоков, каждый с половинной интенсивностью. [19] [20] Свет называется частично поляризованным, когда в одном из этих потоков больше мощности, чем в другом. На любой конкретной длине волны частично поляризованный свет можно статистически описать как суперпозицию полностью неполяризованного компонента и полностью поляризованного. [21] : 346–347 [22] : 330 Затем можно описать свет в терминах степени поляризации и параметров поляризованного компонента. Этот поляризованный компонент можно описать в терминах вектора Джонса или эллипса поляризации. Однако, чтобы также описать степень поляризации, обычно используют параметры Стокса, чтобы указать состояние частичной поляризации. [21] : 351, 374–375Последствия для отражения и распространения
Поляризация при распространении волн
В вакууме компоненты электрического поля распространяются со скоростью света , так что фаза волны меняется в пространстве и времени, а состояние поляризации — нет. То есть вектор электрического поля e плоской волны в направлении + z имеет вид:
где k — волновое число . Как отмечено выше, мгновенное электрическое поле — это действительная часть произведения вектора Джонса на фазовый множитель . Когда электромагнитная волна взаимодействует с веществом, ее распространение изменяется в соответствии с (комплексным) показателем преломления материала . Когда действительная или мнимая часть этого показателя преломления зависит от состояния поляризации волны, свойств, известных как двулучепреломление и поляризационный дихроизм (или диаттенюация ) соответственно, то состояние поляризации волны, как правило, будет изменено.
В таких средах электромагнитная волна с любым заданным состоянием поляризации может быть разложена на две ортогонально поляризованные компоненты, которые сталкиваются с различными постоянными распространения . Влияние распространения по заданному пути на эти два компонента проще всего охарактеризовать в виде комплексного Матрица преобразования J размером 2 × 2 , известная как матрица Джонса :
Матрица Джонса, возникающая при прохождении через прозрачный материал, зависит от расстояния распространения, а также от двупреломления. Двупреломление (как и средний показатель преломления) обычно является дисперсионным , то есть оно будет изменяться в зависимости от оптической частоты (длины волны). Однако в случае недвупреломляющих материаловМатрица Джонса размером 2 × 2 является единичной матрицей (умноженной на скалярный фазовый множитель и множитель затухания), что подразумевает отсутствие изменения поляризации во время распространения.
Для эффектов распространения в двух ортогональных модах матрицу Джонса можно записать как
где g 1 и g 2 — комплексные числа, описывающие задержку фазы и, возможно, затухание амплитуды из-за распространения в каждой из двух собственных мод поляризации . T — унитарная матрица , представляющая изменение базиса от этих мод распространения к линейной системе, используемой для векторов Джонса; в случае линейного двулучепреломления или диатенюации моды сами являются линейными состояниями поляризации, поэтому T и T −1 можно опустить, если оси координат были выбраны соответствующим образом.
Двойное лучепреломление
В двупреломляющем веществе электромагнитные волны различной поляризации распространяются с разной скоростью ( фазовой скоростью ). В результате, когда неполяризованные волны проходят через пластину двупреломляющего материала, одна компонента поляризации имеет более короткую длину волны, чем другая, что приводит к разности фаз между компонентами, которая увеличивается по мере того, как волны проходят через материал. Матрица Джонса является унитарной матрицей : | g 1 | = | g 2 | = 1. Среды, называемые диаттенуирующими (или дихроичными в смысле поляризации), в которых только амплитуды двух поляризаций подвергаются дифференцированному воздействию, могут быть описаны с помощью эрмитовой матрицы (обычно умноженной на общий фазовый множитель). Фактически, поскольку любая матрица может быть записана как произведение унитарной и положительной эрмитовой матриц, распространение света через любую последовательность оптических компонентов, зависящих от поляризации, может быть записано как произведение этих двух основных типов преобразований.

В двупреломляющих средах нет затухания, но две моды накапливают дифференциальную фазовую задержку. Хорошо известные проявления линейного двупреломления (то есть, когда базисные поляризации являются ортогональными линейными поляризациями) появляются в оптических волновых пластинах /замедлителях и многих кристаллах. Если линейно поляризованный свет проходит через двупреломляющий материал, его состояние поляризации, как правило, изменится, если только направление его поляризации не будет идентично одному из этих базисных поляризаций. Поскольку сдвиг фазы и, следовательно, изменение состояния поляризации, как правило, зависят от длины волны, такие объекты, рассматриваемые под белым светом между двумя поляризаторами, могут вызывать цветные эффекты, как видно на прилагаемой фотографии.
Круговое двупреломление также называется оптической активностью , особенно в хиральных жидкостях, или вращением Фарадея , когда из-за наличия магнитного поля вдоль направления распространения. Когда линейно поляризованный свет проходит через такой объект, он выйдет по-прежнему линейно поляризованным, но с повернутым направлением оси поляризации. Комбинация линейного и кругового двупреломления будет иметь в качестве базовых поляризаций две ортогональные эллиптические поляризации; однако термин «эллиптическое двупреломление» используется редко.
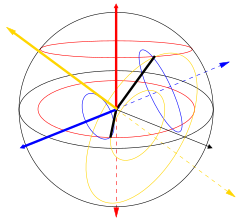
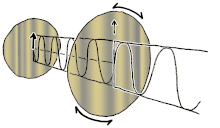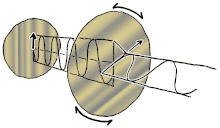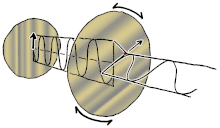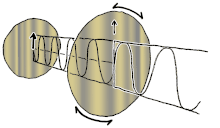
Можно визуализировать случай линейного двулучепреломления (с двумя ортогональными линейными модами распространения) с входящей волной, линейно поляризованной под углом 45° к этим модам. По мере того, как дифференциальная фаза начинает накапливаться, поляризация становится эллиптической, в конечном итоге изменяясь на чисто круговую поляризацию (разность фаз 90°), затем на эллиптическую и в конечном итоге на линейную поляризацию (фаза 180°), перпендикулярную исходной поляризации, затем снова через круговую (фаза 270°), затем эллиптическую с исходным азимутальным углом и, наконец, обратно в исходное линейно поляризованное состояние (фаза 360°), где цикл начинается заново. В целом ситуация более сложная и может быть охарактеризована как вращение в сфере Пуанкаре вокруг оси, определяемой модами распространения. Примеры линейного (синего), кругового (красного) и эллиптического (желтого) двулучепреломления показаны на рисунке слева. Общая интенсивность и степень поляризации не изменяются. Если длина пути в двупреломляющей среде достаточна, два поляризационных компонента коллимированного пучка (или луча ) могут выйти из материала с позиционным смещением, даже если их окончательные направления распространения будут одинаковыми (предполагая, что входная и выходная поверхности параллельны). Обычно это наблюдается с помощью кристаллов кальцита , которые представляют наблюдателю два слегка смещенных изображения, в противоположных поляризациях, объекта за кристаллом. Именно этот эффект обеспечил первое открытие поляризации Эразмом Бартолинусом в 1669 году.
Дихроизм
Среды, в которых преимущественно снижается прохождение одной поляризационной моды, называются дихроичными или диаттенюирующими . Подобно двулучепреломлению, диаттенюация может быть по отношению к линейным поляризационным модам (в кристалле) или круговым поляризационным модам (обычно в жидкости).
Устройства, которые блокируют почти все излучение в одном режиме, известны как поляризационные фильтры или просто « поляризаторы ». Это соответствует g 2 = 0 в приведенном выше представлении матрицы Джонса. Выход идеального поляризатора представляет собой определенное состояние поляризации (обычно линейную поляризацию) с амплитудой, равной исходной амплитуде входной волны в этом режиме поляризации. Мощность в другом режиме поляризации устраняется. Таким образом, если неполяризованный свет пропускается через идеальный поляризатор (где g 1 = 1 и g 2 = 0 ), сохраняется ровно половина его первоначальной мощности. Практические поляризаторы, особенно недорогие листовые поляризаторы, имеют дополнительные потери, так что g 1 < 1. Однако во многих случаях более важным показателем качества является степень поляризации или коэффициент экстинкции поляризатора , которые включают сравнение g 1 с g 2 . Поскольку векторы Джонса относятся к амплитудам волн (а не к интенсивности ) , при освещении неполяризованным светом остаточная мощность в нежелательной поляризации составит ( g2 / g1 ) 2 от мощности в предполагаемой поляризации.
Зеркальное отражение
Помимо двулучепреломления и дихроизма в протяженных средах, поляризационные эффекты, описываемые с помощью матриц Джонса, могут также возникать на (отражающем) интерфейсе между двумя материалами с различным показателем преломления . Эти эффекты рассматриваются уравнениями Френеля . Часть волны передается, а часть отражается; для данного материала эти пропорции (а также фаза отражения) зависят от угла падения и различны для s- и p -поляризаций. Поэтому состояние поляризации отраженного света (даже если изначально он неполяризован) обычно изменяется.

Любой свет, падающий на поверхность под особым углом падения, известным как угол Брюстера , где коэффициент отражения для p -поляризации равен нулю, будет отражаться, оставляя только s -поляризацию. Этот принцип используется в так называемом «поляризаторе со стопкой пластин» (см. рисунок), в котором часть s -поляризации удаляется путем отражения на каждой поверхности угла Брюстера, оставляя только p -поляризацию после прохождения через множество таких поверхностей. Обычно меньший коэффициент отражения p -поляризации также является основой поляризованных солнцезащитных очков ; блокируя s- (горизонтальную) поляризацию, удаляется большая часть бликов, вызванных отражением от мокрой улицы, например. [23] : 348–350
В важном частном случае отражения при нормальном падении (не включающем анизотропные материалы) нет особой s- или p -поляризации. Как x-, так и y- компоненты поляризации отражаются одинаково, и поэтому поляризация отраженной волны идентична поляризации падающей волны. Однако в случае круговой (или эллиптической) поляризации направленность состояния поляризации тем самым меняется на противоположную, поскольку по соглашению это указывается относительно направления распространения. Круговое вращение электрического поля вокруг осей xy , называемое «правым» для волны в направлении + z, является «левым» для волны в направлении − z . Но в общем случае отражения при ненулевом угле падения такое обобщение сделать нельзя. Например, право-кругово поляризованный свет, отраженный от диэлектрической поверхности под углом скольжения, все равно будет право- (но эллиптически) поляризованным. Линейно поляризованный свет, отраженный от металла при ненормальном падении, обычно становится эллиптически поляризованным. Эти случаи обрабатываются с использованием векторов Джонса, на которые действуют различные коэффициенты Френеля для s- и p -компонент поляризации.
Методы измерения с использованием поляризации
Некоторые оптические методы измерения основаны на поляризации. Во многих других оптических методах поляризация имеет решающее значение или, по крайней мере, должна учитываться и контролироваться; таких примеров слишком много, чтобы их перечислять.
Измерение стресса

В инженерии явление двупреломления, вызванного напряжением, позволяет легко наблюдать напряжения в прозрачных материалах. Как отмечено выше и показано на прилагаемой фотографии, хроматичность двупреломления обычно создает цветные узоры при наблюдении между двумя поляризаторами. При приложении внешних сил наблюдается внутреннее напряжение, вызванное в материале. Кроме того, двупреломление часто наблюдается из-за напряжений, «замороженных» во время производства. Это хорошо заметно в целлофановой ленте, двупреломление которой обусловлено растяжением материала в процессе производства.
Эллипсометрия
Эллипсометрия — это мощный метод измерения оптических свойств однородной поверхности. Он включает измерение состояния поляризации света после зеркального отражения от такой поверхности. Обычно это делается как функция угла падения или длины волны (или того и другого). Поскольку эллипсометрия основана на отражении, не требуется, чтобы образец был прозрачным для света или чтобы его задняя сторона была доступна.
Эллипсометрию можно использовать для моделирования (комплексного) показателя преломления поверхности объемного материала. Она также очень полезна при определении параметров одного или нескольких слоев тонкой пленки, нанесенных на подложку. Благодаря своим отражательным свойствам , не только прогнозируется величина p- и s -компонент поляризации, но и их относительные фазовые сдвиги при отражении по сравнению с измерениями с использованием эллипсометра. Обычный эллипсометр измеряет не фактический коэффициент отражения (что требует тщательной фотометрической калибровки освещающего луча), а соотношение p- и s -отражений, а также изменение эллиптичности поляризации (отсюда и название), вызванное отражением изучаемой поверхностью. Помимо использования в науке и исследованиях, эллипсометры используются in situ, например, для контроля производственных процессов. [24] : 585ff [25] : 632
Геология

Свойство (линейного) двупреломления широко распространено в кристаллических минералах и, действительно, имело решающее значение в первоначальном открытии поляризации. В минералогии это свойство часто используется с использованием поляризационных микроскопов для идентификации минералов. Подробнее см. в разделе «Оптическая минералогия» . [26] : 163–164
Звуковые волны в твердых материалах проявляют поляризацию. Дифференциальное распространение трех поляризаций через землю имеет решающее значение в области сейсмологии . Горизонтально и вертикально поляризованные сейсмические волны ( сдвиговые волны ) называются SH и SV, тогда как волны с продольной поляризацией ( сжатые волны ) называются P-волнами. [27] : 48–50 [28] : 56–57
Вскрытие
Аналогичным образом поляризационные микроскопы могут использоваться для обнаружения инородных тел в срезах биологических тканей, если они обладают двойным лучепреломлением; при вскрытии часто упоминается (отсутствие или наличие) «поляризующихся инородных тел». [29]
Химия
Мы видели (выше), что двупреломление типа кристалла полезно для его идентификации, и, таким образом, обнаружение линейного двупреломления особенно полезно в геологии и минералогии . Линейно поляризованный свет обычно имеет измененное состояние поляризации при прохождении через такой кристалл, что делает его выделяющимся при просмотре между двумя скрещенными поляризаторами, как показано на фотографии выше. Аналогично, в химии вращение осей поляризации в жидком растворе может быть полезным измерением. В жидкости линейное двупреломление невозможно, но может быть круговое двупреломление, когда хиральная молекула находится в растворе. Когда правые и левые энантиомеры такой молекулы присутствуют в равных количествах (так называемая рацемическая смесь), то их эффекты нейтрализуются. Однако, когда есть только один (или преобладание одного), как это чаще всего бывает в случае органических молекул , наблюдается чистое круговое двойное лучепреломление (или оптическая активность ), показывающее величину этого дисбаланса (или концентрацию самой молекулы, когда можно предположить, что присутствует только один энантиомер). Это измеряется с помощью поляриметра , в котором поляризованный свет пропускается через трубку с жидкостью, на конце которой находится другой поляризатор, который вращается, чтобы свести к нулю пропускание света через него. [23] : 360–365 [30]
Астрономия
Во многих областях астрономии изучение поляризованного электромагнитного излучения из внешнего космоса имеет большое значение. Хотя поляризация обычно не является фактором теплового излучения звезд , она также присутствует в излучении когерентных астрономических источников (например, гидроксильных или метанольных мазеров ) и некогерентных источников, таких как большие радиолепестки в активных галактиках и радиоизлучение пульсаров (которое, как предполагается, иногда может быть когерентным), а также накладывается на звездный свет путем рассеяния от межзвездной пыли . Помимо предоставления информации об источниках излучения и рассеяния, поляризация также исследует межзвездное магнитное поле посредством вращения Фарадея . [31] : 119, 124 [32] : 336–337 Поляризация космического микроволнового фона используется для изучения физики очень ранней Вселенной. [33] [34] Синхротронное излучение по своей природе поляризовано. Было высказано предположение, что астрономические источники стали причиной хиральности биологических молекул на Земле [35] , но в качестве альтернативной теории был предложен отбор хиральности на неорганических кристаллах [36] .
Приложения и примеры
Поляризованные солнцезащитные очки


Неполяризованный свет, отражаясь от зеркальной (блестящей) поверхности, обычно приобретает некоторую степень поляризации. Это явление наблюдал в начале 1800-х годов математик Этьен-Луи Малус , в честь которого назван закон Малуса . Поляризационные солнцезащитные очки используют этот эффект для уменьшения бликов от отражений от горизонтальных поверхностей, в частности от дороги впереди, видимой под углом скольжения.
Владельцы поляризованных солнцезащитных очков иногда будут наблюдать непреднамеренные эффекты поляризации, такие как цветозависимые эффекты двойного лучепреломления, например, в закаленном стекле (например, окна автомобиля) или предметах из прозрачного пластика , в сочетании с естественной поляризацией путем отражения или рассеивания. Поляризованный свет от ЖК-мониторов (см. ниже) чрезвычайно заметен, когда их носят.
Поляризация неба и фотография

Поляризация наблюдается в свете неба , поскольку это происходит из-за солнечного света, рассеиваемого аэрозолями при прохождении через атмосферу Земли . Рассеянный свет создает яркость и цвет в ясном небе. Эта частичная поляризация рассеянного света может использоваться для затемнения неба на фотографиях, увеличивая контраст. Этот эффект наиболее сильно наблюдается в точках на небе, составляющих угол 90° к Солнцу. Поляризационные фильтры используют эти эффекты для оптимизации результатов фотографирования сцен, в которых задействовано отражение или рассеивание небом. [23] : 346–347 [37] : 495–499

Поляризация неба использовалась для ориентации в навигации. Небесный компас Пфунда использовался в 1950-х годах при навигации вблизи полюсов магнитного поля Земли, когда ни солнца , ни звезд не было видно (например, под дневными облаками или в сумерках ). Было высказано спорное предположение, что викинги использовали похожее устройство (« солнечный камень ») в своих обширных экспедициях через Северную Атлантику в IX–XI веках, до прибытия магнитного компаса из Азии в Европу в XII веке. С небесным компасом связаны « полярные часы », изобретенные Чарльзом Уитстоном в конце XIX века. [38] : 67–69
Технологии отображения
Принцип технологии жидкокристаллического дисплея (ЖКД) основан на вращении оси линейной поляризации жидкокристаллической матрицей. Свет от подсветки (или заднего отражающего слоя в устройствах, не включающих или не требующих подсветки) сначала проходит через линейный поляризационный лист. Этот поляризованный свет проходит через фактический жидкокристаллический слой, который может быть организован в пикселях (для телевизора или компьютерного монитора) или в другом формате, таком как семисегментный дисплей или дисплей с пользовательскими символами для конкретного продукта. Жидкокристаллический слой создается с последовательной правой (или левой) хиральностью, по сути, состоящей из крошечных спиралей . Это вызывает круговое двулучепреломление и спроектировано таким образом, чтобы имело место вращение на 90 градусов состояния линейной поляризации. Однако, когда напряжение подается на ячейку, молекулы выпрямляются, уменьшая или полностью теряя круговое двулучепреломление. На видимой стороне дисплея находится еще один линейный поляризационный лист, обычно ориентированный на 90 градусов от того, который находится за активным слоем. Поэтому, когда круговое двулучепреломление устраняется приложением достаточного напряжения, поляризация проходящего света остается под прямым углом к переднему поляризатору, и пиксель выглядит темным. Однако при отсутствии напряжения поворот поляризации на 90 градусов заставляет ее точно соответствовать оси переднего поляризатора, позволяя свету проходить. Промежуточные напряжения создают промежуточное вращение оси поляризации, и пиксель имеет промежуточную интенсивность. Дисплеи, основанные на этом принципе, широко распространены и теперь используются в подавляющем большинстве телевизоров, компьютерных мониторов и видеопроекторах, что делает предыдущую технологию ЭЛТ по существу устаревшей. Использование поляризации в работе ЖК-дисплеев сразу же очевидно для человека, носящего поляризованные солнцезащитные очки, что часто делает дисплей нечитаемым.
В совершенно ином смысле поляризационное кодирование стало ведущим (но не единственным) методом передачи отдельных изображений для левого и правого глаза на стереоскопических дисплеях, используемых для 3D-фильмов . Это включает в себя отдельные изображения, предназначенные для каждого глаза, либо проецируемые с двух разных проекторов с ортогонально ориентированными поляризационными фильтрами, либо, что более типично, с одного проектора с мультиплексированной по времени поляризацией (устройство быстрой чередующейся поляризации для последовательных кадров). Поляризованные 3D-очки с подходящими поляризационными фильтрами гарантируют, что каждый глаз получает только предполагаемое изображение. Исторически такие системы использовали линейное поляризационное кодирование, поскольку оно было недорогим и обеспечивало хорошее разделение. Однако круговая поляризация делает разделение двух изображений нечувствительным к наклону головы и широко используется в сегодняшнем показе 3D-фильмов, например, система от RealD . Проецирование таких изображений требует экранов, которые поддерживают поляризацию проецируемого света при просмотре в отражении (например, серебряные экраны ); обычный диффузный белый проекционный экран вызывает деполяризацию проецируемых изображений, что делает его непригодным для этого применения.
Хотя сейчас ЭЛТ-дисплеи уже устарели, они страдали от отражения стеклянной оболочкой, что вызывало блики от комнатного освещения и, как следствие, плохой контраст. Для решения этой проблемы было использовано несколько антибликовых решений. Одно из решений использовало принцип отражения кругово-поляризованного света. Круговой поляризационный фильтр перед экраном позволяет пропускать (скажем) только правый кругово-поляризованный комнатный свет. Теперь правый кругово-поляризованный свет (в зависимости от используемого соглашения ) имеет направление своего электрического (и магнитного) поля, вращающееся по часовой стрелке при распространении в направлении +z. При отражении поле по-прежнему имеет то же направление вращения, но теперь распространение происходит в направлении −z, делая отраженную волну левой кругово-поляризованной. При размещении правого кругового поляризационного фильтра перед отражающим стеклом нежелательный свет, отраженный от стекла, будет, таким образом, находиться в том самом состоянии поляризации, которое блокируется этим фильтром, устраняя проблему отражения. Изменение круговой поляризации при отражении и устранение отражений таким образом можно легко наблюдать, глядя в зеркало, надев 3D-очки, которые используют левую и правую круговую поляризацию в двух линзах. Закрывая один глаз, другой глаз будет видеть отражение, в котором он не может видеть себя; эта линза кажется черной. Однако другая линза (закрытого глаза) будет иметь правильную круговую поляризацию, позволяя открытому глазу легко видеть закрытый глаз.
Радиопередача и прием
Все радиоантенны (и микроволновые) , используемые для передачи или приема, по своей природе поляризованы. Они передают сигналы в определенной поляризации (или принимают их), будучи совершенно нечувствительными к противоположной поляризации; в некоторых случаях эта поляризация является функцией направления. Большинство антенн номинально имеют линейную поляризацию, но возможна эллиптическая и круговая поляризация. В случае линейной поляризации возможен тот же тип фильтрации, что описан выше. В случае эллиптической поляризации (круговая поляризация на самом деле является просто разновидностью эллиптической поляризации, где длина обоих коэффициентов упругости одинакова), отфильтровывание одного угла (например, 90°) практически не окажет никакого влияния, поскольку волна в любой момент времени может находиться в любом из 360 градусов.
Подавляющее большинство антенн линейно поляризованы. Фактически, можно показать из соображений симметрии, что антенна, которая полностью лежит в плоскости, которая также включает наблюдателя, может иметь поляризацию только в направлении этой плоскости. Это применимо ко многим случаям, что позволяет легко вывести поляризацию такой антенны в предполагаемом направлении распространения. Так, типичная антенна Yagi на крыше или логопериодическая антенна с горизонтальными проводниками, если смотреть со второй станции в направлении горизонта, обязательно горизонтально поляризована. Но вертикальная « штыревая антенна » или вещательная башня AM, используемая в качестве антенного элемента (опять же, для наблюдателей, горизонтально смещенных от нее), будет передавать в вертикальной поляризации. Турникетная антенна с четырьмя плечами в горизонтальной плоскости также передает горизонтально поляризованное излучение в направлении горизонта. Однако, когда та же самая турникетная антенна используется в «аксиальном режиме» (вверх, для той же горизонтально ориентированной структуры), ее излучение имеет круговую поляризацию. На промежуточных высотах оно имеет эллиптически поляризованное.
Поляризация важна в радиосвязи, потому что, например, если попытаться использовать горизонтально поляризованную антенну для приема вертикально поляризованной передачи, сила сигнала будет существенно снижена (или при очень контролируемых условиях сведена к нулю). Этот принцип используется в спутниковом телевидении для того, чтобы удвоить пропускную способность канала в фиксированном диапазоне частот. Один и тот же частотный канал может использоваться для двух сигналов, транслируемых в противоположных поляризациях. Настраивая приемную антенну на одну или другую поляризацию, можно выбрать любой сигнал без помех от другого.
Особенно из-за наличия земли , существуют некоторые различия в распространении (а также в отражениях, ответственных за телевизионные ореолы ) между горизонтальной и вертикальной поляризацией. AM и FM-вещательные радиостанции обычно используют вертикальную поляризацию, в то время как телевидение использует горизонтальную поляризацию. На низких частотах, особенно, горизонтальная поляризация избегается. Это происходит потому, что фаза горизонтально поляризованной волны меняется на противоположную при отражении от земли. Удаленная станция в горизонтальном направлении будет принимать как прямую, так и отраженную волну, которые, таким образом, имеют тенденцию подавлять друг друга. Эта проблема избегается с помощью вертикальной поляризации. Поляризация также важна при передаче радиолокационных импульсов и приеме радиолокационных отражений той же или другой антенной. Например, обратного рассеяния радиолокационных импульсов каплями дождя можно избежать, используя круговую поляризацию. Так же, как зеркальное отражение кругово поляризованного света изменяет направленность поляризации, как обсуждалось выше, тот же принцип применяется к рассеянию объектами, намного меньшими, чем длина волны, такими как капли дождя. С другой стороны, отражение этой волны от нерегулярного металлического объекта (например, самолета) обычно приводит к изменению поляризации и (частичному) приему отраженной волны той же антенной.
Эффект свободных электронов в ионосфере , в сочетании с магнитным полем Земли , вызывает вращение Фарадея , своего рода круговое двулучепреломление. Это тот же механизм, который может вращать ось линейной поляризации электронами в межзвездном пространстве , как упомянуто ниже. Величина вращения Фарадея, вызванного такой плазмой, значительно преувеличена на более низких частотах, поэтому на более высоких микроволновых частотах, используемых спутниками, эффект минимален. Однако средне- или коротковолновые передачи, полученные после рефракции ионосферой, сильно затронуты. Поскольку путь волны через ионосферу и вектор магнитного поля Земли вдоль такого пути довольно непредсказуемы, волна, переданная с вертикальной (или горизонтальной) поляризацией, как правило, будет иметь результирующую поляризацию в произвольной ориентации на приемнике.

Поляризация и зрение
Многие животные способны воспринимать некоторые компоненты поляризации света, например, линейный горизонтально поляризованный свет. Это обычно используется в навигационных целях, поскольку линейная поляризация небесного света всегда перпендикулярна направлению солнца. Эта способность очень распространена среди насекомых , включая пчел , которые используют эту информацию для ориентации своих коммуникативных танцев . [38] : 102–103 Чувствительность к поляризации также наблюдалась у видов осьминогов , кальмаров , каракатиц и раков-богомолов . [38] : 111–112 В последнем случае один вид измеряет все шесть ортогональных компонентов поляризации и, как полагают, имеет оптимальное поляризационное зрение. [39] Быстро меняющиеся, ярко окрашенные узоры кожи каракатиц, используемые для общения, также включают узоры поляризации, а раки-богомолы, как известно, имеют поляризационно-избирательную отражательную ткань. Считалось, что поляризация неба воспринимается голубями , что, как предполагалось, является одним из средств, помогающих им ориентироваться , но исследования показывают, что это популярный миф. [40]
Невооруженный человеческий глаз слабо чувствителен к поляризации, без необходимости использования промежуточных фильтров. Поляризованный свет создает очень слабый рисунок вблизи центра поля зрения, называемый щеткой Хайдингера . Этот рисунок очень трудно увидеть, но с практикой можно научиться обнаруживать поляризованный свет невооруженным глазом. [38] : 118
Угловой момент с использованием круговой поляризации
Хорошо известно, что электромагнитное излучение несет определенный линейный импульс в направлении распространения. Кроме того, свет несет определенный угловой момент , если он имеет круговую поляризацию (или частично). По сравнению с более низкими частотами, такими как микроволны, величина углового момента в свете , даже чисто круговой поляризации, по сравнению с линейным импульсом той же волны (или давлением излучения ) очень мала и ее трудно даже измерить. Тем не менее, она была использована в эксперименте для достижения скоростей до 600 миллионов оборотов в минуту. [41] [42]
Смотрите также
Квантовая физика
Оптика
Ссылки
Ссылки на цитируемую литературу
- ^ Шипман, Джеймс; Уилсон, Джерри Д.; Хиггинс, Чарльз А. (2015). Введение в физическую науку, 14-е изд. Cengage Learning. стр. 187. ISBN 978-1-305-54467-3.
- ^ Манкастер, Роджер (1993). Физика уровня A. Нельсон Торнес. С. 465–467. ISBN 0-7487-1584-3.
- ^ Сингх, Деврадж (2015). Основы оптики, 2-е изд. PHI Learning Pvt. Ltd. стр. 453. ISBN 978-8120351462.
- ^ ab Avadhanulu, MN (1992). Учебник инженерной физики. S. Chand Publishing. стр. 198–199. ISBN 8121908175.
- ^ Демаре, Луи (1997). Прикладная электрооптика. Pearson Education. С. 162–163. ISBN 0-13-244182-9.
- ^ Le Tiec, A.; Novak, J. (июль 2016 г.). «Теория гравитационных волн». Обзор гравитационных волн . стр. 1–41. arXiv : 1607.04202 . doi :10.1142/9789813141766_0001. ISBN 978-981-314-175-9. S2CID 119283594.
- ^ Липсон, Стивен Г.; Липсон, Генри; Тангейзер, Дэвид Стефан (1995). Оптическая физика. Cambridge University Press. С. 125–127. ISBN 978-0-521-43631-1.
- ^ ab Waldman, Gary (2002). Введение в свет: физика света, зрения и цвета. Courier Corporation. стр. 79–80. ISBN 978-0-486-42118-6.
- ^ Гриффитс, Дэвид Дж. (1998). Введение в электродинамику (3-е изд.). Prentice Hall. ISBN 0-13-805326-X.
- ^ Джеффри Нью (7 апреля 2011 г.). Введение в нелинейную оптику . Cambridge University Press. ISBN 978-1-139-50076-0.
- ^ Dorn, R.; Quabis, S. & Leuchs, G. (декабрь 2003 г.). "Более четкий фокус для радиально поляризованного светового луча". Physical Review Letters . 91 (23): 233901. Bibcode :2003PhRvL..91w3901D. doi :10.1103/PhysRevLett.91.233901. PMID 14683185.
- ^ Чандрасекар, Субраманьян (1960). Radiative Transfer . Dover. стр. 27. ISBN 0-486-60590-6. OCLC 924844798.
- ^ ab Sletten, Mark A.; Mc Laughlin, David J. (2005-04-15). "Radar Polarimetry". В Chang, Kai (ред.). Encyclopedia of RF and Microwave Engineering . John Wiley & Sons, Inc. doi :10.1002/0471654507.eme343. ISBN 978-0-471-65450-6.
- ^ Шранк, Гельмут Э.; Эванс, Гэри Э.; Дэвис, Дэниел (1990). «6 рефлекторных антенн» (PDF) . В Скольнике, Меррилл Иван (ред.). Справочник по радару (PDF) . МакГроу-Хилл. стр. 6.30, рис. 6.25. ISBN 978-0-07-057913-2. Архивировано (PDF) из оригинала 2022-10-09.
- ^ Ишии, Т. Корю, ред. (1995). Справочник по микроволновой технологии. Том 2: Приложения. Elsevier. стр. 177. ISBN 978-0-08-053410-7.
- ^ Волакис, Джон (2007). Справочник по антенной инженерии, четвертое издание. McGraw-Hill. Раздел 26.1. ISBN 9780071475747: Примечание : в отличие от других авторов, этот источник изначально определяет эллиптичность взаимно, как отношение малой оси к большой, но затем продолжает, что «Хотя [она] меньше единицы, при выражении эллиптичности в децибелах знак минус часто опускается для удобства», что по сути возвращается к определению, принятому другими авторами.
{{cite book}}: CS1 maint: postscript (link) - ^ Чипман, РА; Лэм, У.С.Т.; Янг, Г. (2018). Поляризованный свет и оптические системы. Оптические науки и применение света. CRC Press. ISBN 978-1-4987-0057-3. Получено 2023-01-20 .
- ^ Шарма, КК (2006). Оптика: принципы и приложения. Elsevier Science. стр. 145. ISBN 978-0-08-046391-9. Получено 2023-01-20 .
- ^ Пракаш, Хари; Чандра, Нареш (1971). «Оператор плотности неполяризованного излучения». Physical Review A. 4 ( 2): 796–799. Bibcode :1971PhRvA...4..796P. doi :10.1103/PhysRevA.4.796.
- ^ Чандрасекар, Субраманьян (2013). Перенос излучения . Курьер. стр. 30.
- ^ ab Hecht, Eugene (2002). Optics (4-е изд.). Соединенные Штаты Америки: Addison Wesley. ISBN 0-8053-8566-5.
- ^ Бекефи, Джордж; Барретт, Алан (1977). Электромагнитные колебания, волны и излучение . США: MIT Press. ISBN 0-262-52047-8.
- ^ abc Hecht, Eugene (2002). Optics (4-е изд.). Соединенные Штаты Америки: Addison Wesley. ISBN 0-8053-8566-5.
- ^ Деннис Голдштейн; Деннис Х. Голдштейн (3 января 2011 г.). Поляризованный свет, исправленный и расширенный . CRC Press. ISBN 978-0-203-91158-7.
- ^ Масуд Мансурипур (2009). Классическая оптика и ее приложения . Cambridge University Press. ISBN 978-0-521-88169-2.
- ^ Рэнди О. Уэйн (16 декабря 2013 г.). Световая и видеомикроскопия . Academic Press. ISBN 978-0-12-411536-1.
- ^ Питер М. Ширер (2009). Введение в сейсмологию . Cambridge University Press. ISBN 978-0-521-88210-1.
- ^ Seth Stein; Michael Wysession (1 апреля 2009 г.). Введение в сейсмологию, землетрясения и структуру Земли . John Wiley & Sons. ISBN 978-1-4443-1131-0.
- ^ Алави, Файзан; Шилдс, Бриджит Э.; Омолехинва, Темитопе; Розенбах, Миша (01.10.2020). «Гранулематозная болезнь полости рта». Дерматологические клиники . Пероральная медицина в дерматологии. 38 (4): 429–439. doi :10.1016/j.det.2020.05.004. ISSN 0733-8635.
- ^ Vollhardt, K. Peter C.; Schore, Neil E. (2003). Органическая химия: структура и функция (4-е изд.). WH Freeman . стр. 169–172. ISBN 978-0-7167-4374-3.
- ^ Vlemmings, WHT (март 2007 г.). «Обзор поляризации мазера и магнитных полей». Труды Международного астрономического союза . 3 (S242): 37–46. arXiv : 0705.0885 . Bibcode : 2007IAUS..242...37V . doi : 10.1017/s1743921307012549 .
- ^ Ханну Карттунен; Пекка Крёгер; Хейкки Оя (27 июня 2007 г.). Фундаментальная астрономия . Спрингер. ISBN 978-3-540-34143-7.
- ^ Boyle, Latham A.; Steinhardt, PJ; Turok, N (2006). «Пересмотр инфляционных предсказаний для скалярных и тензорных флуктуаций». Physical Review Letters . 96 (11): 111301. arXiv : astro-ph/0507455 . Bibcode :2006PhRvL..96k1301B. doi :10.1103/PhysRevLett.96.111301. PMID 16605810. S2CID 10424288.
- ^ Тегмарк, Макс (2005). «Что на самом деле предсказывает инфляция?». Журнал космологии и астрофизики частиц . 0504 (4): 001. arXiv : astro-ph/0410281 . Bibcode : 2005JCAP...04..001T. doi : 10.1088/1475-7516/2005/04/001. S2CID 17250080.
- ^ Кларк, С. (1999). «Поляризованный звездный свет и ручность жизни». American Scientist . 97 (4): 336–43. Bibcode : 1999AmSci..87..336C. doi : 10.1511/1999.4.336. S2CID 221585816.
- ^ Хазен, Роберт М.; Шолл, Дэвид С. (2003-06-01). «Хиральный отбор на неорганических кристаллических поверхностях». Nature Materials . 2 (6): 367–374. doi :10.1038/nmat879. ISSN 1476-1122.
- ^ Бекефи, Джордж; Барретт, Алан (1977). Электромагнитные колебания, волны и излучение . США: MIT Press. ISBN 0-262-52047-8.
- ^ abcd J. David Pye (13 февраля 2001 г.). Поляризованный свет в науке и природе . CRC Press. ISBN 978-0-7503-0673-7.
- ^ Соня Кляйнлогель; Эндрю Уайт (2008). «Тайный мир креветок: поляризационное видение в лучшем виде». PLOS ONE . 3 (5): e2190. arXiv : 0804.2162 . Bibcode : 2008PLoSO...3.2190K. doi : 10.1371/journal.pone.0002190 . PMC 2377063. PMID 18478095 .
- ^ Nuboer, JFW; Coemans, M. a. JM; Vos Hzn, JJ (1995-02-01). «Нет доказательств поляризационной чувствительности в электроретинограмме голубя». Journal of Experimental Biology . 198 (2): 325–335. doi : 10.1242/jeb.198.2.325 . ISSN 0022-0949. PMID 9317897. Архивировано из оригинала 27.08.2019 . Получено 27.08.2019 .
- ^ "Создан 'Самый быстро вращающийся объект'". BBC News . 2013-08-28. Архивировано из оригинала 2019-09-10 . Получено 2019-08-27 .
- ^ Dholakia, Kishan; Mazilu, Michael; Arita, Yoshihiko (28 августа 2013 г.). «Вращение и охлаждение захваченного микрогироскопа под действием лазерного излучения в вакууме». Nature Communications . 4 : 2374. Bibcode : 2013NatCo...4.2374A. doi : 10.1038/ncomms3374. hdl : 10023/4019. PMC 3763500. PMID 23982323 .
Общие ссылки
- Аззам, Р. М. А.; Башара, Н. М. (1977). Эллипсометрия и поляризованный свет . Северная Голландия. ISBN 0-444-87016-4.
- Борн, М.; Вольф, Э. (1999). Принципы оптики (7-е изд.). Кембриджский университет. ISBN 0-521-64222-1.
- Броссо, К. (1998). Основы поляризованного света: статистический оптический подход . Wiley. ISBN 0-471-14302-2.
- Коллетт, Эдвард (2005). Полевое руководство по поляризации . SPIE Field Guides. Том FG05. SPIE. ISBN 0-8194-5868-6.
- Дамаск, Джей Н. (2004). Поляризационная оптика в телекоммуникациях . Springer. ISBN 0-387-22493-9.
- Goldstein, Dennis; Dekker, Marcel (2003). Поляризованный свет (2-е изд.). Taylor & Francis. ISBN 0-8247-4053-X.
- Карлсен, Лейф (2003). Секреты мореплавателей-викингов: как викинги использовали свои удивительные солнечные камни и другие методы для пересечения открытых океанов . One Earth Press.
- Кённен, ГП (1985). Поляризованный свет в природе . Перевод Бирлинга, GA Кембриджский университет. ISBN 0-521-25862-6.
- Пай, Дэвид (2001). Поляризованный свет в науке и природе . Институт физики. ISBN 0-7503-0673-4.
- Шерклифф, Уильям А. (1962). Поляризованный свет, производство и использование . Гарвардский университет.
Внешние ссылки
- Лекция Фейнмана о поляризации
- Галерея цифровых изображений в поляризованном свете: микроскопические изображения, полученные с использованием эффектов поляризации
- MathPages: Связь между спином фотона и поляризацией
- Виртуальный поляризационный микроскоп
- Угол поляризации в спутниковых антеннах.
- Молекулярные выражения: наука, оптика и вы — Поляризация света: интерактивное руководство по Java
- Поляризация антенны
- Анимации линейной, круговой и эллиптической поляризации на YouTube