Электрическое сопротивление и проводимость
| Статьи о |
| Электромагнетизм |
|---|
 |
| Электрическое сопротивление | |
|---|---|
Общие символы | Р |
| единица СИ | Ом (Ом) |
| В основных единицах СИ | кг⋅м 2 ⋅с −3 ⋅А −2 |
| Измерение | |
| Электропроводность | |
|---|---|
Общие символы | Г |
| единица СИ | сименс (С) |
| В основных единицах СИ | кг −1 ⋅м −2 ⋅с 3 ⋅А 2 |
Выводы из других величин | |
| Измерение | |
Электрическое сопротивление объекта является мерой его противодействия потоку электрического тока . Его обратная величина равнаэлектропроводность , измеряющая легкость прохождения электрического тока. Электрическое сопротивление имеет некоторые концептуальные параллели с механическимтрением.в системе СИявляетсяом( Ω ), тогда как электропроводность измеряется всименсах(S) (ранее называвшихся «мхо» и затем представленных как℧).
Сопротивление объекта во многом зависит от материала, из которого он сделан. Объекты, сделанные из электроизоляторов, таких как резина, как правило, имеют очень высокое сопротивление и низкую проводимость, в то время как объекты, сделанные из электропроводников, таких как металлы, как правило, имеют очень низкое сопротивление и высокую проводимость. Эта связь количественно определяется удельным сопротивлением или проводимостью . Однако природа материала не является единственным фактором сопротивления и проводимости; она также зависит от размера и формы объекта, поскольку эти свойства являются скорее экстенсивными, чем интенсивными . Например, сопротивление провода выше, если он длинный и тонкий, и ниже, если он короткий и толстый. Все объекты сопротивляются электрическому току, за исключением сверхпроводников , сопротивление которых равно нулю.
Сопротивление R объекта определяется как отношение напряжения V на нем к току I через него, тогда как проводимость G является обратной величиной:
Для широкого спектра материалов и условий V и I прямо пропорциональны друг другу, и поэтому R и G являются константами (хотя они будут зависеть от размера и формы объекта, материала, из которого он сделан, и других факторов, таких как температура или деформация ). Эта пропорциональность называется законом Ома , а материалы, которые ему удовлетворяют, называются омическими материалами.
В других случаях, таких как трансформатор , диод или батарея , V и I не являются прямо пропорциональными. Отношение В/я иногда все еще полезно и называется хордовым сопротивлением или статическим сопротивлением , [1] [2], поскольку оно соответствует обратному наклону хорды между началом координат и кривой I – V. В других ситуациях производная может быть наиболее полезной; это называется дифференциальным сопротивлением .
Введение

В гидравлической аналогии ток, текущий по проводу (или резистору ), подобен воде, текущей по трубе, а падение напряжения на проводе подобно падению давления , которое толкает воду по трубе. Проводимость пропорциональна тому, какой поток происходит при заданном давлении, а сопротивление пропорционально тому, какое давление требуется для достижения заданного потока.
Падение напряжения ( т. е. разница между напряжениями на одной стороне резистора и на другой), а не само напряжение , обеспечивает движущую силу, проталкивающую ток через резистор. В гидравлике это похоже: разница давлений между двумя сторонами трубы, а не само давление, определяет поток через нее. Например, над трубой может быть большое давление воды, которое пытается протолкнуть воду вниз по трубе. Но может быть такое же большое давление воды под трубой, которое пытается протолкнуть воду обратно вверх по трубе. Если эти давления равны, вода не течет. (На изображении справа давление воды под трубой равно нулю.)
Сопротивление и проводимость провода, резистора или другого элемента в основном определяются двумя свойствами:
- геометрия (форма) и
- материал
Геометрия важна, поскольку проталкивать воду через длинную узкую трубу сложнее, чем через широкую короткую трубу. Точно так же длинная тонкая медная проволока имеет большее сопротивление (меньшую проводимость), чем короткая толстая медная проволока.
Материалы также важны. Труба, заполненная волосами, ограничивает поток воды больше, чем чистая труба той же формы и размера. Аналогично, электроны могут свободно и легко проходить через медный провод, но не могут так же легко проходить через стальной провод той же формы и размера, и они по сути вообще не могут проходить через изолятор, такой как резина , независимо от его формы. Разница между медью, сталью и резиной связана с их микроскопической структурой и электронной конфигурацией и количественно определяется свойством, называемым удельным сопротивлением .
Помимо геометрии и материала, существуют и другие факторы, влияющие на сопротивление и проводимость, такие как температура; см. ниже.
Проводники и резисторы

Вещества, в которых может течь электричество, называются проводниками . Кусок проводящего материала с определенным сопротивлением, предназначенный для использования в цепи, называется резистором . Проводники изготавливаются из материалов с высокой проводимостью , таких как металлы, в частности медь и алюминий. Резисторы, с другой стороны, изготавливаются из самых разных материалов в зависимости от таких факторов, как желаемое сопротивление, количество энергии, которое необходимо рассеять, точность и стоимость.
Закон Ома

Для многих материалов ток I через материал пропорционален напряжению V, приложенному к нему: в широком диапазоне напряжений и токов. Поэтому сопротивление и проводимость объектов или электронных компонентов, изготовленных из этих материалов, постоянны. Это соотношение называется законом Ома , а материалы, которые ему подчиняются, называются омическими материалами. Примерами омических компонентов являются провода и резисторы . График зависимости тока от напряжения омического устройства представляет собой прямую линию, проходящую через начало координат с положительным наклоном .
Другие компоненты и материалы, используемые в электронике, не подчиняются закону Ома; ток не пропорционален напряжению, поэтому сопротивление меняется в зависимости от напряжения и тока через них. Они называются нелинейными или неомическими . Примерами являются диоды и люминесцентные лампы .
Связь с удельным сопротивлением и проводимостью

Сопротивление данного объекта зависит в первую очередь от двух факторов: из какого материала он сделан и от его формы. Для данного материала сопротивление обратно пропорционально площади поперечного сечения; например, толстый медный провод имеет меньшее сопротивление, чем в остальном идентичный тонкий медный провод. Также для данного материала сопротивление пропорционально длине; например, длинный медный провод имеет большее сопротивление, чем в остальном идентичный короткий медный провод. Сопротивление R и проводимость G проводника постоянного поперечного сечения, таким образом, можно вычислить как
где — длина проводника, измеряемая в метрах (м), A — площадь поперечного сечения проводника, измеряемая в квадратных метрах (м 2 ), σ ( сигма ) — электропроводность, измеряемая в сименсах на метр (См·м −1 ), а ρ ( ро ) — удельное электрическое сопротивление (также называемое удельным электрическим сопротивлением ) материала, измеряемое в ом-метрах (Ом·м). Удельное сопротивление и проводимость являются константами пропорциональности и, следовательно, зависят только от материала, из которого сделан провод, а не от геометрии провода. Удельное сопротивление и проводимость являются обратными величинами : . Удельное сопротивление — это мера способности материала противостоять электрическому току.
Эта формула не точна, поскольку предполагает, что плотность тока в проводнике полностью однородна, что не всегда верно в практических ситуациях. Однако эта формула все еще обеспечивает хорошее приближение для длинных тонких проводников, таких как провода.
Другая ситуация, для которой эта формула не точна, — это переменный ток (AC), поскольку скин-эффект препятствует току вблизи центра проводника. По этой причине геометрическое поперечное сечение отличается от эффективного поперечного сечения, в котором фактически течет ток, поэтому сопротивление выше ожидаемого. Аналогично, если два проводника рядом друг с другом несут переменный ток, их сопротивление увеличивается из-за эффекта близости . На промышленной частоте питания эти эффекты значительны для больших проводников, несущих большие токи, таких как шины на электрической подстанции , [3] или большие силовые кабели, несущие более нескольких сотен ампер.
Удельное сопротивление различных материалов различается на огромную величину: например, проводимость тефлона примерно в 10 30 раз ниже проводимости меди. Грубо говоря, это происходит потому, что металлы имеют большое количество «делокализованных» электронов, которые не застревают ни в одном месте, поэтому они могут свободно перемещаться на большие расстояния. В изоляторе, таком как тефлон, каждый электрон прочно связан с одной молекулой, поэтому требуется большая сила, чтобы вырвать его. Полупроводники находятся между этими двумя крайностями. Более подробную информацию можно найти в статье: Удельное электрическое сопротивление и проводимость . В случае растворов электролитов см. статью: Проводимость (электролитическая) .
Удельное сопротивление меняется в зависимости от температуры. В полупроводниках удельное сопротивление также меняется под воздействием света. См. ниже.
Измерение

Прибор для измерения сопротивления называется омметром . Простые омметры не могут точно измерять низкие сопротивления, поскольку сопротивление их измерительных проводов вызывает падение напряжения, которое мешает измерению, поэтому более точные приборы используют четырехконтактное зондирование .
Типичные значения
| Компонент | Сопротивление (Ом) |
|---|---|
| 1 метр медной проволоки диаметром 1 мм | 0,02 [а] |
| 1 км воздушной линии электропередачи ( типичная ) | 0,03 [5] |
| Батарея АА ( типичное внутреннее сопротивление ) | 0,1 [б] |
| Нить накаливания лампы ( типичная ) | 200–1000 [с] |
| Тело человека | 1000–100 000 [д] |
Статическое и дифференциальное сопротивление
Многие электрические элементы, такие как диоды и батареи, не удовлетворяют закону Ома . Они называются неомическими или нелинейными , и их кривые тока и напряжения не являются прямыми линиями, проходящими через начало координат.
Сопротивление и проводимость все еще могут быть определены для неомических элементов. Однако, в отличие от омического сопротивления, нелинейное сопротивление не является постоянным, а изменяется в зависимости от напряжения или тока через устройство; т. е. его рабочей точки . Существует два типа сопротивления: [1] [2]
- Статическое сопротивление
Это соответствует обычному определению сопротивления: напряжение, деленное на ток.
Это наклон линии ( хорды ) от начала координат через точку на кривой. Статическое сопротивление определяет рассеиваемую мощность в электрическом компоненте. Точки на кривой тока-напряжения, расположенные во 2-м или 4-м квадрантах, для которых наклон хордальной линии отрицателен, имеют отрицательное статическое сопротивление . Пассивные устройства, не имеющие источника энергии, не могут иметь отрицательное статическое сопротивление. Однако активные устройства, такие как транзисторы или операционные усилители, могут синтезировать отрицательное статическое сопротивление с обратной связью, и оно используется в некоторых схемах, таких как гираторы .- Дифференциальное сопротивление
Это производная напряжения по току; наклон кривой ток-напряжение в точке
Если кривая тока-напряжения немонотонна ( с пиками и впадинами), кривая имеет отрицательный наклон в некоторых областях, поэтому в этих областях устройство имеет отрицательное дифференциальное сопротивление . Устройства с отрицательным дифференциальным сопротивлением могут усиливать сигнал, подаваемый на них, и используются для создания усилителей и генераторов. К ним относятся туннельные диоды , диоды Ганна , диоды IMPATT , магнетронные трубки и однопереходные транзисторы .
Цепи переменного тока
Сопротивление и проводимость
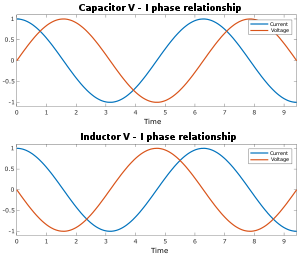
Когда переменный ток протекает через цепь, соотношение между током и напряжением на элементе цепи характеризуется не только отношением их величин, но и разницей в их фазах . Например, в идеальном резисторе в момент, когда напряжение достигает своего максимума, ток также достигает своего максимума (ток и напряжение колеблются в фазе). Но для конденсатора или катушки индуктивности максимальный ток возникает, когда напряжение проходит через ноль и наоборот (ток и напряжение колеблются на 90° в противофазе, см. изображение ниже). Комплексные числа используются для отслеживания как фазы, так и величины тока и напряжения:
где:
- t — время;
- u ( t ) и i ( t ) — напряжение и ток как функции времени соответственно;
- U 0 и I 0 обозначают амплитуду напряжения и тока соответственно;
- - угловая частота переменного тока;
- - угол смещения;
- U и I — комплексные значения напряжения и тока соответственно;
- Z и Y — комплексное сопротивление и проводимость соответственно;
- указывает действительную часть комплексного числа ; и
- — мнимая единица .
Импеданс и проводимость могут быть выражены в виде комплексных чисел, которые можно разбить на действительную и мнимую части:
где R — сопротивление, G — проводимость, X — реактивное сопротивление , а B — реактивная проводимость . Это приводит к комплексным числовым тождествам , которые верны во всех случаях, тогда как верны только в особых случаях постоянного тока или тока без реактивного сопротивления.
Комплексный угол — это разность фаз между напряжением и током, проходящим через компонент с импедансом Z. Для конденсаторов и индукторов этот угол равен точно -90° или +90° соответственно, а X и B не равны нулю. Идеальные резисторы имеют угол 0°, так как X равен нулю (и, следовательно, B тоже), а Z и Y сокращаются до R и G соответственно. В общем случае системы переменного тока проектируются так, чтобы поддерживать фазовый угол максимально близким к 0°, так как это снижает реактивную мощность , которая не выполняет никакой полезной работы на нагрузке. В простом случае с индуктивной нагрузкой (вызывающей увеличение фазы) можно добавить конденсатор для компенсации на одной частоте, так как сдвиг фазы конденсатора отрицателен, что снова приближает фазу общего импеданса к 0°.
Y является обратной величиной Z ( ) для всех цепей, так же как для цепей постоянного тока, содержащих только резисторы, или цепей переменного тока, для которых либо реактивное сопротивление, либо реактивная проводимость равны нулю ( X или B = 0 соответственно) (если одно из них равно нулю, то для реальных систем оба должны быть равны нулю).
Частотная зависимость
Ключевой особенностью цепей переменного тока является то, что сопротивление и проводимость могут зависеть от частоты, явление, известное как универсальный диэлектрический отклик . [8] Одной из причин, упомянутых выше, является скин-эффект (и связанный с ним эффект близости ). Другая причина заключается в том, что само удельное сопротивление может зависеть от частоты (см. модель Друде , ловушки с глубоким уровнем , резонансная частота , соотношения Крамерса–Кронига и т. д.)
Рассеивание энергии и джоулев нагрев

Резисторы (и другие элементы с сопротивлением) противодействуют электрическому току; поэтому для проталкивания тока через сопротивление требуется электрическая энергия. Эта электрическая энергия рассеивается, нагревая резистор в процессе. Это называется джоулевым нагревом (в честь Джеймса Прескотта Джоуля ), также называемым омическим нагревом или резистивным нагревом .
Рассеивание электроэнергии часто нежелательно, особенно в случае потерь при передаче в линиях электропередач . Высоковольтная передача помогает снизить потери за счет снижения тока для заданной мощности.
С другой стороны, джоулев нагрев иногда полезен, например, в электрических плитах и других электрических нагревателях (также называемых резистивными нагревателями ). Другой пример: лампы накаливания используют джоулев нагрев: нить накаливания нагревается до такой высокой температуры, что она светится «добела» с помощью теплового излучения (также называемого накаливанием ).
Формула для расчета джоулева тепла выглядит следующим образом: где P — мощность (энергия в единицу времени), преобразованная из электрической энергии в тепловую, R — сопротивление, а I — ток через резистор.
Зависимость от других условий
Температурная зависимость
Вблизи комнатной температуры удельное сопротивление металлов обычно увеличивается с ростом температуры, тогда как удельное сопротивление полупроводников обычно уменьшается с ростом температуры. Удельное сопротивление изоляторов и электролитов может увеличиваться или уменьшаться в зависимости от системы. Подробное поведение и объяснение см. в разделе Удельное сопротивление и проводимость .
В результате сопротивление проводов, резисторов и других компонентов часто меняется в зависимости от температуры. Этот эффект может быть нежелательным, вызывая сбои в работе электронной схемы при экстремальных температурах. Однако в некоторых случаях этот эффект используется с пользой. Когда температурно-зависимое сопротивление компонента используется целенаправленно, компонент называется термометром сопротивления или термистором . (Термометр сопротивления изготавливается из металла, обычно платины, тогда как термистор изготавливается из керамики или полимера.)
Термометры сопротивления и термисторы обычно используются двумя способами. Во-первых, их можно использовать в качестве термометров : измеряя сопротивление, можно определить температуру окружающей среды. Во-вторых, их можно использовать в сочетании с джоулевым нагревом (также называемым самонагревом): если через резистор проходит большой ток, температура резистора повышается, и, следовательно, его сопротивление изменяется. Поэтому эти компоненты можно использовать в качестве защиты цепи, аналогичной предохранителям , или для обратной связи в цепях, или для многих других целей. В общем, самонагрев может превратить резистор в нелинейный и гистерезисный элемент цепи. Более подробную информацию см. в разделе Термистор#Эффекты самонагрева .
Если температура T не меняется слишком сильно, обычно используется линейная аппроксимация : где называется температурным коэффициентом сопротивления , - фиксированная опорная температура (обычно комнатная температура), а - сопротивление при температуре . Параметр - это эмпирический параметр, подобранный из данных измерений. Поскольку линейная аппроксимация является лишь приближением, отличается для разных опорных температур. По этой причине обычно указывают температуру, при которой была измерена, с суффиксом, например , и эта связь сохраняется только в диапазоне температур вокруг опорной. [9]
Температурный коэффициент обычно равен+3 × 10 −3 К−1 в+6 × 10−3 K−1 для металлов при температуре , близкой к комнатной. Обычно отрицательна для полупроводников и изоляторов, с сильно изменчивой величиной. [e]
Зависимость от деформации
Так же, как сопротивление проводника зависит от температуры, сопротивление проводника зависит от деформации . [10] При натяжении проводника (форма напряжения , которая приводит к деформации в виде растяжения проводника) длина участка проводника под натяжением увеличивается, а площадь его поперечного сечения уменьшается. Оба эти эффекта способствуют увеличению сопротивления деформированного участка проводника. При сжатии (деформации в противоположном направлении) сопротивление деформированного участка проводника уменьшается. См. обсуждение тензодатчиков для получения подробной информации об устройствах, сконструированных для использования этого эффекта.
Зависимость освещенности от света
Некоторые резисторы, особенно те, что сделаны из полупроводников , проявляют фотопроводимость , то есть их сопротивление изменяется при попадании на них света. Поэтому их называют фоторезисторами (или светозависимыми резисторами ). Это распространенный тип детекторов света .
Сверхпроводимость
Сверхпроводники — это материалы, которые имеют точно нулевое сопротивление и бесконечную проводимость, потому что они могут иметь V = 0 и I ≠ 0. Это также означает, что нет джоулева нагрева , или, другими словами, нет рассеивания электрической энергии. Поэтому, если сверхпроводящий провод сделать замкнутым контуром, ток будет течь по контуру вечно. Сверхпроводники требуют охлаждения до температур, близких к4 К с жидким гелием для большинства металлических сверхпроводников, таких как сплавы ниобия и олова , или охлаждение до температур, близких к77 К с жидким азотом для дорогих, хрупких и деликатных керамических высокотемпературных сверхпроводников . Тем не менее, существует множество технологических применений сверхпроводимости , включая сверхпроводящие магниты .
Смотрите также
- Квант проводимости
- Константа фон Клитцинга (обратная ей величина)
- Электрические измерения
- Контактное сопротивление
- Электрическое сопротивление и проводимость для получения дополнительной информации о физических механизмах проводимости в материалах.
- Шум Джонсона-Найквиста
- Квантовый эффект Холла , стандарт для высокоточных измерений сопротивления.
- Резистор
- РКМ-код
- Последовательные и параллельные цепи
- Сопротивление слоя
- Единицы измерения электромагнетизма в системе СИ
- Термическое сопротивление
- Делитель напряжения
- Падение напряжения
Сноски
- ^ Удельное сопротивление меди составляет около1,7 × 10 −8 Ом⋅м . [4]
- ^ Для новой щелочной батарейки Energizer E91 AA внутреннее сопротивление варьируется от0,9 Ом при−40 °C , до0,1 Ом при+40 °C . [6]
- ^ АЛампочка накаливания 60 Вт (в США с120 В сетевое электричество ) потребляет среднеквадратичный ток 60 Вт/120 В =500 мА , поэтому его сопротивление равно 120 В/500 мА =240 Ом . СопротивлениеЛампочка накаливания 60 Вт в Европе (230 В сеть)900 Ом . Сопротивление нити накаливания зависит от температуры; эти значения действительны для случая, когда нить накаливания уже нагрета и свет уже горит.
- ^ 100 кОм для контакта с сухой кожей,1 кОм для контакта с мокрой или поврежденной кожей. Высокое напряжение разрушает кожу, снижая сопротивление500 Ω . Другие факторы и условия также имеют значение. Для получения более подробной информации см. статью об электрошоке и NIOSH 98-131. [7]
- ^ См. таблицу Электрическое сопротивление и проводимость . Температурный коэффициент сопротивления похож, но не идентичен температурному коэффициенту сопротивления. Небольшая разница обусловлена тепловым расширением, изменяющим размеры резистора.
Ссылки
- ^ ab Brown, Forbes T. (2006). Engineering System Dynamics: A Unified Graph-Centered Approach (2-е изд.). Бока-Ратон, Флорида: CRC Press. стр. 43. ISBN 978-0-8493-9648-9.
- ^ ab Kaiser, Kenneth L. (2004). Справочник по электромагнитной совместимости. Бока-Ратон, Флорида: CRC Press. С. 13–52. ISBN 978-0-8493-2087-3.
- ^ Fink & Beaty (1923). «Стандартный справочник для инженеров-электриков». Nature . 111 (2788) (11-е изд.): 17–19. Bibcode :1923Natur.111..458R. doi :10.1038/111458a0. hdl : 2027/mdp.39015065357108 . S2CID 26358546.
- ^ Катнелл, Джон Д.; Джонсон, Кеннет В. (1992). Физика (2-е изд.). Нью-Йорк: Wiley. С. 559. ISBN 978-0-471-52919-4.
- ^ Макдональд, Джон Д. (2016). Проектирование электрических подстанций (2-е изд.). Бока-Ратон, Флорида: CRC Press. стр. 363 и далее. ISBN 978-1-4200-0731-2.
- ^ Внутреннее сопротивление батареи (PDF) (Отчет). Energizer Corp. Архивировано из оригинала (PDF) 11 января 2012 года . Получено 13 декабря 2011 года .
- ^ "Смерть рабочих от удара током" (PDF) . Национальный институт охраны труда . Публикация № 98-131 . Получено 2 ноября 2014 г. .
- ^ Zhai, Chongpu; Gan, Yixiang; Hanaor, Dorian; Proust, Gwénaëlle (2018). «Электрический транспорт, зависящий от напряжения, и его универсальное масштабирование в гранулированных материалах». Extreme Mechanics Letters . 22 : 83–88. arXiv : 1712.05938 . Bibcode : 2018ExML...22...83Z. doi : 10.1016/j.eml.2018.05.005. S2CID 51912472.
- ^ Уорд, М. Р. (1971). Электротехническая наука . McGraw-Hill. С. 36–40.
- ^ Мейер, Себастьян и др. (2022), «Характеристика деформационного состояния магния по электрическому сопротивлению», том 215 , Scripta Materialia, т. 215, стр. 114712, doi : 10.1016/j.scriptamat.2022.114712 , S2CID 247959452
Внешние ссылки
- «Калькулятор сопротивления». Лаборатория автомобильной электроники. Университет Клемсона. Архивировано из оригинала 11 июля 2010 г.
- «Модели электронной проводимости с использованием случайных блужданий с максимальной энтропией». wolfram.com . Проект демонстраций Wolfram.






![{\displaystyle {\begin{aligned}R&=\rho {\frac {\ell }{A}},\\[5pt]G&=\sigma {\frac {A}{\ell }}\,.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b24667605c2703efd09de736ebc63d30be931418)
















![{\displaystyle R(T)=R_{0}[1+\альфа (T-T_{0})]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5b6622ab35566bd32d26736effa752dc8ace798d)





