Случайное блуждание

Часть серии по статистике
Теория вероятностей
Вероятность Аксиомы Детерминизм Система Индетерминизм Случайность
Вероятностное пространство Образец пространства Событие В совокупности исчерпывающие события Элементарное событие Взаимная исключительность Исход Синглтон Эксперимент процесс Бернулли Распределение вероятностей Распределение Бернулли Биномиальное распределение Экспоненциальное распределение Нормальное распределение Распределение Парето Распределение Пуассона Мера вероятности Случайная величина процесс Бернулли Непрерывный или дискретный Ожидаемое значение Дисперсия цепь Маркова Наблюдаемое значение Случайное блуждание Случайный процесс
Complementary event Joint probability Marginal probability Conditional probability
Independence Conditional independence Law of total probability Law of large numbers Bayes' theorem Boole's inequality
Venn diagram Tree diagram
v t e

В математике случайное блуждание , иногда называемое « прогулкой пьяницы» , — это стохастический процесс , описывающий путь, состоящий из последовательности случайных шагов в некотором математическом пространстве .

Элементарным примером случайного блуждания является случайное блуждание по прямой целых чисел , которое начинается с 0 и на каждом шаге перемещается на +1 или −1 с равной вероятностью . Другие примеры включают путь, проложенный молекулой , когда она движется в жидкости или газе (см. Броуновское движение ), путь поиска животного , ищущего пищу , или цену колеблющейся акции и финансовое положение игрока . Случайные блуждания имеют приложения к инженерии и многим научным областям, включая экологию , психологию , информатику , физику , химию , биологию , экономику и социологию . Термин «случайное блуждание» был впервые введен Карлом Пирсоном в 1905 году. ^[1]${\displaystyle \mathbb {Z} }$

Реализации случайных блужданий могут быть получены с помощью моделирования Монте-Карло . ^[2]

Популярная модель случайного блуждания — это модель случайного блуждания по регулярной решетке, где на каждом шаге местоположение переходит на другой сайт в соответствии с некоторым распределением вероятностей. В простом случайном блуждании местоположение может переходить только на соседние сайты решетки, образуя путь решетки . В простом симметричном случайном блуждании по локально конечной решетке вероятности перехода местоположения к каждому из его непосредственных соседей одинаковы. Наиболее изученным примером является случайное блуждание по d -мерной целочисленной решетке (иногда называемой гиперкубической решеткой) . ^[3]${\displaystyle \mathbb {Z} ^{d}}$

Если пространство состояний ограничено конечными размерами, модель случайного блуждания называется простым симметричным случайным блужданием с границей , а вероятности перехода зависят от местоположения состояния, поскольку в пограничных и угловых состояниях движение ограничено. ^[4]

Простейшим примером случайного блуждания является случайное блуждание по прямой целых чисел, которое начинается с 0 и на каждом шаге перемещается на +1 или −1 с равной вероятностью.${\displaystyle \mathbb {Z} }$

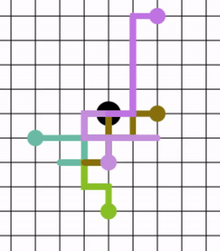
Эту прогулку можно проиллюстрировать следующим образом. Маркер помещается на нулевую позицию на числовой прямой, и подбрасывается честная монета. Если выпадает орел, маркер перемещается на одну единицу вправо. Если выпадает решка, маркер перемещается на одну единицу влево. После пяти подбрасываний маркер может оказаться на -5, -3, -1, 1, 3, 5. При пяти подбрасываниях, трех орлах и двух решках в любом порядке он приземлится на 1. Существует 10 способов приземлиться на 1 (перевернув три орла и две решки), 10 способов приземлиться на −1 (перевернув три решки и два орла), 5 способов приземлиться на 3 (перевернув четыре орла и одну решку), 5 способов приземлиться на −3 (перевернув четыре решки и одну решку), 1 способ приземлиться на 5 (перевернув пять орлов) и 1 способ приземлиться на −5 (перевернув пять решек). На рисунке ниже показаны возможные результаты 5 подбрасываний.

Чтобы формально определить этот блуждание, возьмем независимые случайные величины , где каждая переменная равна 1 или −1 с вероятностью 50% для любого значения, и установим и Ряд называется простым случайным блужданием по . Этот ряд (сумма последовательности −1 и 1 ) дает чистое пройденное расстояние, если каждая часть блуждания имеет длину один. Математическое ожидание равно нулю. То есть среднее значение всех подбрасываний монеты стремится к нулю по мере увеличения числа подбрасываний. Это следует из свойства конечной аддитивности математического ожидания:${\displaystyle Z_{1},Z_{2},\dots }$${\displaystyle S_{0}=0}$${\textstyle S_{n}=\sum _{j=1}^{n}Z_{j}.}$ ${\displaystyle \{S_{n}\}}$${\displaystyle \mathbb {Z} }$ ${\displaystyle E(S_{n})}$${\displaystyle S_{n}}$$${\displaystyle E(S_{n})=\sum _{j=1}^{n}E(Z_{j})=0.}$$

Аналогичный расчет, использующий независимость случайных величин и тот факт, что , показывает, что:${\displaystyle E(Z_{n}^{2})=1}$$${\displaystyle E(S_{n}^{2})=\sum _{i=1}^{n}E(Z_{i}^{2})+2\sum _{1\leq i<j\leq n}E(Z_{i}Z_{j})=n.}$$

Это намекает , что ожидаемое расстояние перевода после n шагов должно быть порядка . Фактически, ^[5]${\displaystyle E(|S_{n}|)\,\!}$ ${\displaystyle {\sqrt {n}}}$$${\displaystyle \lim _{n\to \infty }{\frac {E(|S_{n}|)}{\sqrt {n}}}={\sqrt {\frac {2}{\pi }}}.}$$

Чтобы ответить на вопрос, сколько раз случайное блуждание пересечет граничную линию, если ему будет разрешено продолжать идти вечно, простое случайное блуждание пересечет каждую точку бесконечное число раз. У этого результата есть много названий: явление пересечения уровня , повторение или разорение игрока . Причина последнего названия следующая: игрок с конечной суммой денег в конечном итоге проиграет, играя в честную игру против банка с бесконечной суммой денег. Деньги игрока совершат случайное блуждание, и в какой-то момент достигнут нуля, и игра будет окончена.${\displaystyle \mathbb {Z} }$

Если a и b — положительные целые числа, то ожидаемое количество шагов до того, как одномерное простое случайное блуждание, начинающееся с 0, впервые попадет в b или − a , равно ab . Вероятность того, что это блуждание попадет в b до − a , равна , что можно вывести из того факта, что простое случайное блуждание является мартингалом . И эти ожидания и вероятности попадания можно вычислить в общей одномерной цепи Маркова случайного блуждания.${\displaystyle a/(a+b)}$${\displaystyle O(a+b)}$

Некоторые из результатов, упомянутых выше, можно вывести из свойств треугольника Паскаля . Количество различных блужданий из n шагов, где каждый шаг равен +1 или −1, равно 2 ⁿ . Для простого случайного блуждания каждое из этих блужданий равновероятно. Для того чтобы S _n было равно числу k, необходимо и достаточно, чтобы количество +1 в блуждании превышало количество −1 на k . Из этого следует, что +1 должно появляться ( n  +  k )/2 раз среди n шагов блуждания, следовательно, количество блужданий, которые удовлетворяют , равно количеству способов выбора ( n  +  k )/2 элементов из множества n элементов, ^[6] обозначаемых . Для того чтобы это имело смысл, необходимо, чтобы n  +  k было четным числом, что подразумевает, что n и k либо оба четные, либо оба нечетные. Следовательно, вероятность того, что равно . Представляя элементы треугольника Паскаля в терминах факториалов и используя формулу Стирлинга , можно получить хорошие оценки этих вероятностей для больших значений .${\displaystyle S_{n}=k}$${\textstyle n \choose (n+k)/2}$${\displaystyle S_{n}=k}$${\textstyle 2^{-n}{n \choose (n+k)/2}}$${\displaystyle n}$

Если для краткости ограничиться знаком +, то количество способов, которыми случайное блуждание попадет на любое заданное число, имея пять подбрасываний, можно записать как {0,5,0,4,0,1}.${\displaystyle \mathbb {Z} }$

Эта связь с треугольником Паскаля демонстрируется для малых значений n . При нулевом числе оборотов единственной возможностью будет остаться на нуле. Однако при одном обороте есть один шанс приземлиться на −1 или один шанс приземлиться на 1. При двух оборотах маркер на 1 может переместиться на 2 или обратно на ноль. Маркер на −1 может переместиться на −2 или обратно на ноль. Следовательно, есть один шанс приземлиться на −2, два шанса приземлиться на ноль и один шанс приземлиться на 2.

к	−5	−4	−3	−2	−1	0	1	2	3	4	5
${\displaystyle P[S_{0}=k]}$						1
${\displaystyle 2P[S_{1}=k]}$					1		1
${\displaystyle 2^{2}P[S_{2}=k]}$				1		2		1
${\displaystyle 2^{3}P[S_{3}=k]}$			1		3		3		1
${\displaystyle 2^{4}P[S_{4}=k]}$		1		4		6		4		1
${\displaystyle 2^{5}P[S_{5}=k]}$	1		5		10		10		5		1

Центральная предельная теорема и закон повторного логарифма описывают важные аспекты поведения простых случайных блужданий на . В частности, первая подразумевает, что с ростом n вероятности (пропорциональные числам в каждой строке) приближаются к нормальному распределению .${\displaystyle \mathbb {Z} }$

Если быть точным, то, зная это , и используя формулу Стирлинга, можно ${\textstyle \mathbb {P} (X_{n}=k)=2^{-n}{\binom {n}{(n+k)/2}}}$

$${\displaystyle {\log \mathbb {P} (X_{n}=k)}=n\left[\left({1+{\frac {k}{n}}+{\frac {1}{2n}}}\right)\log \left(1+{\frac {k}{n}}\right)+\left({1-{\frac {k}{n}}+{\frac {1}{2n}}}\right)\log \left(1-{\frac {k}{n}}\right)\right]+\log {\frac {\sqrt {2}}{\sqrt {\pi }}}+o(1).}$$

Фиксируя масштабирование для фиксированного и используя расширение при исчезновении, следует ${\textstyle k=\lfloor {\sqrt {n}}x\rfloor }$${\textstyle x}$${\textstyle \log(1+{k}/{n})=k/n-k^{2}/2n^{2}+\dots }$${\textstyle k/n}$

$${\displaystyle {\mathbb {P} \left({\frac {X_{n}}{n}}={\frac {\lfloor {\sqrt {n}}x\rfloor }{\sqrt {n}}}\right)}={\frac {1}{\sqrt {n}}}{\frac {1}{2{\sqrt {\pi }}}}e^{-{x^{2}}}(1+o(1)).}$$

взяв предел (и заметив, что соответствует шагу сетки масштабирования), находим гауссовскую плотность . Действительно, для абсолютно непрерывной случайной величины с плотностью справедливо , с соответствующим бесконечно малым шагом.${\textstyle {1}/{\sqrt {n}}}$${\textstyle f(x)={\frac {1}{2{\sqrt {\pi }}}}e^{-{x^{2}}}}$${\textstyle X}$${\textstyle f_{X}}$${\textstyle \mathbb {P} \left(X\in [x,x+dx)\right)=f_{X}(x)dx}$${\textstyle dx}$

В качестве прямого обобщения можно рассмотреть случайные блуждания по кристаллическим решеткам (бесконечнократные абелевы покрывающие графы над конечными графами). На самом деле, в этой постановке можно установить центральную предельную теорему и теорему о больших отклонениях. ^{[7] [8]}

Одномерное случайное блуждание можно также рассматривать как цепь Маркова , пространство состояний которой задается целыми числами. Для некоторого числа p, удовлетворяющего , вероятности перехода (вероятность P _i,j перехода из состояния i в состояние j ) задаются выражением${\displaystyle i=0,\pm 1,\pm 2,\dots .}$${\displaystyle \,0<p<1}$$${\displaystyle \,P_{i,i+1}=p=1-P_{i,i-1}.}$$

Гетерогенное случайное блуждание рисует на каждом временном шаге случайное число, которое определяет локальные вероятности прыжков, а затем случайное число, которое определяет фактическое направление прыжка. Главный вопрос заключается в вероятности остаться в каждом из различных мест после прыжков, и в пределе этой вероятности, когда очень велико.${\displaystyle t}$${\displaystyle t}$

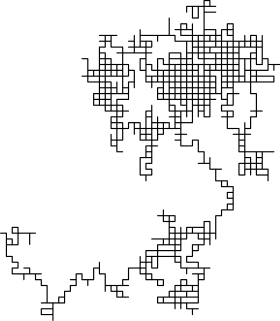
В более высоких измерениях набор случайно пройденных точек обладает интересными геометрическими свойствами. Фактически, получается дискретный фрактал , то есть набор, который демонстрирует стохастическое самоподобие в больших масштабах. В малых масштабах можно наблюдать «зубчатость», возникающую из-за сетки, по которой выполняется прогулка. Траектория случайной прогулки — это набор посещенных точек, рассматриваемых как набор без учета того, когда прогулка достигла точки. В одном измерении траектория — это просто все точки между минимальной высотой и максимальной высотой, достигнутой при прогулке (обе, в среднем, имеют порядок ).${\displaystyle {\sqrt {n}}}$

Чтобы визуализировать двумерный случай, можно представить себе человека, хаотично идущего по городу. Город фактически бесконечен и организован в квадратную сетку тротуаров. На каждом перекрестке человек случайным образом выбирает один из четырех возможных маршрутов (включая тот, по которому изначально ехал). Формально это случайное блуждание по множеству всех точек плоскости с целочисленными координатами .

Чтобы ответить на вопрос о том, вернется ли человек когда-либо в исходную точку прогулки, вот двумерный эквивалент проблемы пересечения уровней, обсуждавшейся выше. В 1921 году Джордж Полиа доказал, что человек почти наверняка вернется в двумерном случайном блуждании, но для трех измерений или выше вероятность возвращения в начало уменьшается с увеличением числа измерений. В трех измерениях вероятность уменьшается примерно до 34%. ^[9] Известно, что математик Сидзуо Какутани ссылался на этот результат следующей цитатой: «Пьяный человек найдет дорогу домой, но пьяная птица может потеряться навсегда». ^[10]

Вероятность повторения в общем случае равна , что можно вывести с помощью производящих функций ^[11] или процесса Пуассона. ^[12]${\displaystyle p=1-\left({\frac {1}{\pi ^{d}}}\int _{[-\pi ,\pi ]^{d}}{\frac {\prod _{i=1}^{d}d\theta _{i}}{1-{\frac {1}{d}}\sum _{i=1}^{d}\cos \theta _{i}}}\right)^{-1}}$

Другой вариант этого вопроса, который также задавал Полиа, звучит так: «если два человека выходят из одной и той же отправной точки, то встретятся ли они когда-нибудь снова?» ^[13] Можно показать, что разница между их местоположениями (два независимых случайных блуждания) также является простым случайным блужданием, поэтому они почти наверняка встретятся снова в двумерном блуждании, но для 3 измерений и выше вероятность уменьшается с числом измерений. Пол Эрдёш и Сэмюэл Джеймс Тейлор также показали в 1960 году, что для измерений, меньших или равных 4, два независимых случайных блуждания, начинающихся из любых двух заданных точек, имеют бесконечно много пересечений почти наверняка, но для измерений выше 5 они почти наверняка пересекаются только конечное число раз. ^[14]

Асимптотическая функция для двумерного случайного блуждания по мере увеличения числа шагов задается распределением Рэлея . Распределение вероятностей является функцией радиуса от начала координат, а длина шага постоянна для каждого шага. Здесь длина шага предполагается равной 1, N — общее число шагов, а r — радиус от начала координат. ^[15]

$${\displaystyle P(r)={\frac {2r}{N}}e^{-r^{2}/N}}$$

Винеровский процесс — это стохастический процесс, поведение которого похоже на броуновское движение , физическое явление диффузии мельчайшей частицы в жидкости. (Иногда винеровский процесс называют «броуновским движением», хотя, строго говоря, это путаница между моделью и моделируемым явлением.)

Процесс Винера — это предел масштабирования случайного блуждания в размерности 1. Это означает, что если есть случайное блуждание с очень малыми шагами, то существует приближение к процессу Винера (и, менее точно, к броуновскому движению). Точнее, если размер шага равен ε, нужно совершить блуждание длиной L /ε ² , чтобы приблизиться к длине Винера L . Когда размер шага стремится к 0 (и число шагов увеличивается пропорционально), случайное блуждание сходится к процессу Винера в соответствующем смысле. Формально, если B — это пространство всех путей длины L с максимальной топологией, а если M — это пространство меры над B с топологией нормы, то сходимость имеет место в пространстве M . Аналогично, процесс Винера в нескольких измерениях — это предел масштабирования случайного блуждания в том же числе измерений.

Случайное блуждание — это дискретный фрактал (функция с целочисленными размерностями; 1, 2, ...), но траектория винеровского процесса — это настоящий фрактал, и между ними есть связь. Например, совершайте случайное блуждание, пока оно не достигнет окружности радиуса r , умноженного на длину шага. Среднее число шагов, которые оно совершает, равно r ² . ^{[ необходима цитата ]} Этот факт является дискретной версией того факта, что блуждание винеровского процесса — это фрактал размерности Хаусдорфа  2. ^{[ необходима цитата ]}

В двух измерениях среднее число точек, которые одно и то же случайное блуждание имеет на границе своей траектории, равно r ^4/3 . Это соответствует тому факту, что граница траектории винеровского процесса является фракталом размерности 4/3, факт, предсказанный Мандельбротом с помощью моделирования, но доказанный только в 2000 году Лоулером , Шраммом и Вернером . ^[16]

Процесс Винера обладает многими симметриями, которых нет у случайного блуждания. Например, блуждание процесса Винера инвариантно к поворотам, но случайное блуждание — нет, поскольку лежащая в основе сетка — нет (случайное блуждание инвариантно к поворотам на 90 градусов, но процессы Винера инвариантны также к поворотам, например, на 17 градусов). Это означает, что во многих случаях проблемы случайного блуждания проще решить, переведя их в процесс Винера, решив задачу там, а затем переведя обратно. С другой стороны, некоторые проблемы проще решить с помощью случайных блужданий из-за их дискретной природы.

Случайное блуждание и винеровский процесс могут быть связаны , а именно проявляться на одном и том же вероятностном пространстве зависимым образом, что заставляет их быть довольно близкими. Простейшей такой связью является вложение Скорохода , но существуют и более точные связи, такие как теорема аппроксимации Комлоша–Майора–Тушнади .

Сходимость случайного блуждания к винеровскому процессу контролируется центральной предельной теоремой и теоремой Донскера . Для частицы в известной фиксированной позиции при t  = 0 центральная предельная теорема говорит нам, что после большого числа независимых шагов в случайном блуждании положение блуждающего распределяется в соответствии с нормальным распределением полной дисперсии :

$${\displaystyle \sigma ^{2}={\frac {t}{\delta t}}\,\varepsilon ^{2},}$$

где t — время, прошедшее с начала случайного блуждания, — размер шага случайного блуждания, — время, прошедшее между двумя последовательными шагами.${\displaystyle \varepsilon }$${\displaystyle \delta t}$

Это соответствует функции Грина уравнения диффузии , контролирующего винеровский процесс, что предполагает, что после большого числа шагов случайное блуждание сходится к винеровскому процессу.

В трехмерном пространстве дисперсия, соответствующая функции Грина уравнения диффузии, равна:$${\displaystyle \sigma ^{2}=6\,D\,t.}$$

Приравнивая эту величину к дисперсии, связанной с положением случайного блуждающего, получаем эквивалентный коэффициент диффузии, который следует учитывать для асимптотического винеровского процесса, к которому случайное блуждание сходится после большого числа шагов: (справедливо только в 3D).$${\displaystyle D={\frac {\varepsilon ^{2}}{6\delta t}}}$$

Два выражения дисперсии выше соответствуют распределению, связанному с вектором , который связывает два конца случайного блуждания, в 3D. Дисперсия, связанная с каждым компонентом , или составляет только одну треть этого значения (все еще в 3D).${\displaystyle {\vec {R}}}$${\displaystyle R_{x}}$${\displaystyle R_{y}}$${\displaystyle R_{z}}$

Для 2D: ^[17]

$${\displaystyle D={\frac {\varepsilon ^{2}}{4\delta t}}.}$$

Для 1D: ^[18]

$${\displaystyle D={\frac {\varepsilon ^{2}}{2\delta t}}.}$$

Случайное блуждание с размером шага, изменяющимся в соответствии с нормальным распределением, используется в качестве модели для реальных временных рядов данных, таких как финансовые рынки.

Здесь размер шага представляет собой обратное кумулятивное нормальное распределение, где 0 ≤  z  ≤ 1 — равномерно распределенное случайное число, а μ и σ — среднее значение и стандартное отклонение нормального распределения соответственно.${\displaystyle \Phi ^{-1}(z,\mu ,\sigma )}$

Если μ не равно нулю, случайное блуждание будет изменяться около линейного тренда. Если v _s — начальное значение случайного блуждания, ожидаемое значение после n шагов будет v _s + n μ.

Для особого случая, когда μ равно нулю, после n шагов распределение вероятностей расстояния перевода задается выражением N (0, n σ ² ), где N () — обозначение нормального распределения, n — число шагов, а σ — из обратного кумулятивного нормального распределения, как указано выше.

Доказательство: Гауссовское случайное блуждание можно рассматривать как сумму последовательности независимых и одинаково распределенных случайных величин, X _i из обратного кумулятивного нормального распределения со средним значением, равным нулю, и σ исходного обратного кумулятивного нормального распределения:

${\displaystyle Z=\sum _{i=0}^{n}{X_{i}},}$

но у нас есть распределение для суммы двух независимых нормально распределенных случайных величин, Z = X + Y , которое задается формулой (см. здесь) . $${\displaystyle {\mathcal {N}}(\mu _{X}+\mu _{Y},\sigma _{X}^{2}+\sigma _{Y}^{2})}$$

В нашем случае μ _X = μ _Y = 0 и σ ² _X = σ ² _Y = σ ² получаем По индукции для n шагов имеем Для шагов, распределенных в соответствии с любым распределением с нулевым средним и конечной дисперсией (не обязательно только нормальным распределением), среднеквадратичное расстояние перевода после n шагов равно (см. тождество Бьенеме )$${\displaystyle {\mathcal {N}}(0,2\sigma ^{2})}$$${\displaystyle Z\sim {\mathcal {N}}(0,n\sigma ^{2}).}$

${\displaystyle {\sqrt {Var(S_{n})}}={\sqrt {E[S_{n}^{2}]}}=\sigma {\sqrt {n}}.}$

Но для гауссовского случайного блуждания это всего лишь стандартное отклонение распределения расстояния трансляции после n шагов. Следовательно, если μ равно нулю, и поскольку среднеквадратичное (RMS) расстояние трансляции равно одному стандартному отклонению, существует 68,27% вероятность того, что RMS расстояние трансляции после n шагов попадет в диапазон . Аналогично, существует 50% вероятность того, что расстояние трансляции после n шагов попадет в диапазон .${\displaystyle \pm \sigma {\sqrt {n}}}$${\displaystyle \pm 0.6745\sigma {\sqrt {n}}}$

Число отдельных мест, посещаемых одним случайным блуждающим, было тщательно изучено для квадратных и кубических решеток и для фракталов. ^{[19] [20]} Эта величина полезна для анализа проблем захвата и кинетических реакций. Она также связана с вибрационной плотностью состояний, ^{[21] [22]} процессами диффузионных реакций ^[23] и распространением популяций в экологии. ^{[24] [25]}${\displaystyle S(t)}$

Скорость информации гауссовского случайного блуждания относительно квадратичного расстояния ошибки, т.е. его квадратичная функция искажения скорости , задается параметрически ^[26] где . Следовательно, невозможно закодировать с помощью двоичного кода размером менее бит и восстановить его с ожидаемой среднеквадратической ошибкой, меньшей . С другой стороны, для любого существует достаточно большой и двоичный код из не более различных элементов такой, что ожидаемая среднеквадратическая ошибка при восстановлении из этого кода не превышает .$${\displaystyle R(D_{\theta })={\frac {1}{2}}\int _{0}^{1}\max\{0,\log _{2}\left(S(\varphi )/\theta \right)\}\,d\varphi ,}$$$${\displaystyle D_{\theta }=\int _{0}^{1}\min\{S(\varphi ),\theta \}\,d\varphi ,}$$${\displaystyle S(\varphi )=\left(2\sin(\pi \varphi /2)\right)^{-2}}$${\displaystyle {\{Z_{n}\}_{n=1}^{N}}}$${\displaystyle NR(D_{\theta })}$ ${\displaystyle D_{\theta }}$${\displaystyle \varepsilon >0}$${\displaystyle N\in \mathbb {N} }$${\displaystyle 2^{NR(D_{\theta })}}$${\displaystyle {\{Z_{n}\}_{n=1}^{N}}}$${\displaystyle D_{\theta }-\varepsilon }$

This section needs additional citations for verification. Please help improve this article by adding citations to reliable sources in this section. Unsourced material may be challenged and removed. (February 2013) (Learn how and when to remove this message)

Как уже упоминалось, диапазон природных явлений, которые были предметом попыток описания с помощью некоторого вида случайных блужданий, значителен, особенно в физике ^{[27] [28]} и химии, ^[29] материаловедении , ^{[30] [31]} и биологии. ^{[32] [33] [34]} Ниже приведены некоторые конкретные применения случайных блужданий:

• В финансовой экономике гипотеза случайного блуждания используется для моделирования цен акций и других факторов. ^[35] Эмпирические исследования обнаружили некоторые отклонения от этой теоретической модели, особенно в краткосрочных и долгосрочных корреляциях. См. цены акций .
• В популяционной генетике случайное блуждание описывает статистические свойства генетического дрейфа.
• В физике случайные блуждания используются как упрощенные модели физического броуновского движения и диффузии, например, случайного движения молекул в жидкостях и газах. См., например, агрегацию, ограниченную диффузией. Также в физике случайные блуждания и некоторые из самовзаимодействующих блужданий играют роль в квантовой теории поля .
• В производстве полупроводников случайные блуждания используются для анализа эффектов термической обработки в более мелких узлах. Они применяются для понимания диффузии легирующих примесей , дефектов , примесей и т. д. во время критических этапов изготовления. Обработки случайными блужданиями также используются для изучения диффузии реагентов, продуктов и плазмы во время процессов химического осаждения из паровой фазы . Континуальная диффузия использовалась для изучения потока газов в макроскопических масштабах в реакторах CVD. Однако меньшие размеры и возросшая сложность заставили нас рассматривать их с помощью случайных блужданий. Это позволяет проводить точный анализ стохастических процессов на молекулярном уровне и меньше в производстве полупроводников.
• В математической экологии случайные блуждания используются для описания индивидуальных перемещений животных, для эмпирического подтверждения процессов биодиффузии и иногда для моделирования динамики популяций .
• В физике полимеров случайное блуждание описывает идеальную цепь . Это самая простая модель для изучения полимеров . ^[36]
• В других областях математики случайное блуждание используется для вычисления решений уравнения Лапласа , для оценки гармонической меры , а также для различных конструкций в анализе и комбинаторике .
• В компьютерной науке случайные блуждания используются для оценки размера Интернета . [ ^37]
• При сегментации изображений случайные блуждания используются для определения меток (например, «объект» или «фон»), которые следует связать с каждым пикселем. ^[38] Этот алгоритм обычно называют алгоритмом сегментации случайных блужданий .

• В исследованиях мозга случайные блуждания и усиленные случайные блуждания используются для моделирования каскадов нейронной активности в мозге.
• В науке о зрении дрейф глаз имеет тенденцию вести себя как случайное блуждание. ^[39] По мнению некоторых авторов, фиксационные движения глаз в целом также хорошо описываются случайным блужданием. ^[40]
• В психологии случайные блуждания точно объясняют связь между временем, необходимым для принятия решения, и вероятностью того, что определенное решение будет принято. ^[41]
• Случайные блуждания можно использовать для выборки из пространства состояний, которое неизвестно или очень велико, например, для выбора случайной страницы из Интернета. ^{[ требуется ссылка ]} В информатике этот метод известен как метод Монте-Карло с цепями Маркова (MCMC).

• В беспроводных сетях для моделирования движения узлов используется случайное блуждание. ^{[ необходима ссылка ]}
• Подвижные бактерии совершают случайные блуждания . ^[42]
• В физике случайные блуждания лежат в основе метода оценки Ферми . ^{[ необходима ссылка ]}
• В Интернете сайт Twitter использует случайные блуждания, чтобы предлагать, за кем следить ^[43]
• Дэйв Байер и Перси Диаконис доказали, что 7 перетасовок достаточно, чтобы перемешать колоду карт (подробнее см. в разделе перетасовка ). Этот результат переводится в утверждение о случайном блуждании по симметричной группе , что они и доказывают, с решающим использованием структуры группы посредством анализа Фурье.

Были рассмотрены несколько типов стохастических процессов , которые похожи на чистые случайные блуждания, но где простая структура может быть более обобщенной. Чистая структура может быть охарактеризована шагами, определяемыми независимыми и одинаково распределенными случайными величинами . Случайные блуждания могут происходить на различных пространствах, таких как графы , целые числа, вещественная прямая, плоскость или многомерные векторные пространства, на криволинейных поверхностях или многообразиях Римана более высокой размерности и на группах . Также возможно определить случайные блуждания, которые совершают свои шаги в случайные моменты времени, и в этом случае положение X
_тдолжно быть определено для всех времен t ∈ [0, +∞) . Конкретные случаи или пределы случайных блужданий включают в себя модели полета Леви и диффузии, такие как броуновское движение .

Случайное блуждание длины k на возможно бесконечном графе G с корнем 0 является стохастическим процессом со случайными величинами, таким что и является вершиной, выбранной равномерно случайным образом из соседей . Тогда число является вероятностью того, что случайное блуждание длины k, начинающееся в v, заканчивается в w . В частности, если G является графом с корнем 0 , является вероятностью того, что -шаговое случайное блуждание возвращается в 0 .${\displaystyle X_{1},X_{2},\dots ,X_{k}}$${\displaystyle X_{1}=0}$${\displaystyle {X_{i+1}}}$${\displaystyle X_{i}}$${\displaystyle p_{v,w,k}(G)}$${\displaystyle p_{0,0,2k}}$${\displaystyle 2k}$

Основываясь на аналогии из предыдущего раздела о более высоких измерениях, предположим теперь, что наш город больше не является идеальной квадратной сеткой. Когда наш человек достигает определенного перекрестка, он выбирает между различными доступными дорогами с равной вероятностью. Таким образом, если перекресток имеет семь съездов, человек поедет на каждый из них с вероятностью одна седьмая. Это случайное блуждание на графике. Дойдет ли наш человек до своего дома? Оказывается, что при довольно мягких условиях ответ все еще да, ^[44] но в зависимости от графика ответ на вариантный вопрос «Встретятся ли два человека снова?» может не быть тем, что они встречаются бесконечно часто почти наверняка. ^[45]

Примером случая, когда человек почти наверняка доберется до своего дома, является случай, когда длины всех блоков находятся в диапазоне от a до b (где a и b — любые два конечных положительных числа). Обратите внимание, что мы не предполагаем, что граф является плоским , т. е. город может содержать туннели и мосты. Один из способов доказать этот результат — использовать подключение к электрическим сетям . Возьмите карту города и поместите резистор сопротивлением 1 Ом на каждый блок. Теперь измерьте «сопротивление между точкой и бесконечностью». Другими словами, выберите некоторое число R и возьмите все точки в электрической сети, расстояние от которой до нашей точки больше R, и соедините их проводами. Теперь это конечная электрическая сеть, и мы можем измерить сопротивление от нашей точки до точек с проводами. Увеличьте R до бесконечности. Предел называется сопротивлением между точкой и бесконечностью . Оказывается, что верно следующее (элементарное доказательство можно найти в книге Дойла и Снелла):

Теорема : граф является переходным тогда и только тогда, когда сопротивление между точкой и бесконечностью конечно. Неважно, какая точка выбрана, если граф связен.

Другими словами, в переходной системе достаточно преодолеть конечное сопротивление, чтобы из любой точки достичь бесконечности. В возвратной системе сопротивление от любой точки до бесконечности бесконечно.

Эта характеристика мимолетности и повторяемости очень полезна и, в частности, позволяет нам проанализировать случай города, нарисованного на плоскости с ограниченными расстояниями.

Случайное блуждание по графу является очень частным случаем цепи Маркова . В отличие от общей цепи Маркова, случайное блуждание по графу обладает свойством, называемым симметрией времени или обратимостью . Грубо говоря, это свойство, также называемое принципом детального баланса , означает, что вероятности прохождения заданного пути в одном или другом направлении имеют очень простую связь между собой (если граф регулярен , они просто равны). Это свойство имеет важные последствия.

Начиная с 1980-х годов, многие исследования были направлены на связь свойств графа со случайными блужданиями. В дополнение к описанной выше электрической сетевой связи, существуют важные связи с изопериметрическими неравенствами , см. больше здесь , функциональными неравенствами, такими как неравенства Соболева и Пуанкаре , и свойствами решений уравнения Лапласа . Значительная часть этих исследований была сосредоточена на графах Кэли конечно порожденных групп . Во многих случаях эти дискретные результаты переносятся на многообразия и группы Ли или выводятся из них .

В контексте случайных графов , в частности модели Эрдёша–Реньи , были получены аналитические результаты для некоторых свойств случайных блуждающих. Они включают распределение первого ^[46] и последнего времени попадания ^[47] блуждающего, где первое время попадания дается первым разом, когда блуждающий ступает на ранее посещенный участок графа, а последнее время попадания соответствует первому разу, когда блуждающий не может выполнить дополнительный ход без повторного посещения ранее посещенного участка.

Хорошим справочником по случайным блужданиям на графах является онлайн-книга Олдоса и Филла. Для групп см. книгу Воесса. Если ядро ​​перехода само по себе случайно (на основе среды ), то случайное блуждание называется «случайным блужданием в случайной среде». Когда закон случайного блуждания включает случайность , закон называется отожженным законом; с другой стороны, если рассматривается как фиксированный, закон называется погашенным законом. См. книгу Хьюза, книгу Ревеса или лекции Зейтуни.${\displaystyle p(x,y)}$${\displaystyle \omega }$${\displaystyle \omega }$${\displaystyle \omega }$

Мы можем думать о выборе каждого возможного ребра с той же вероятностью, что и о локальной максимизации неопределенности (энтропии). Мы также могли бы сделать это глобально — в случайном блуждании с максимальной энтропией (MERW) мы хотим, чтобы все пути были равновероятными, или, другими словами: для каждых двух вершин каждый путь заданной длины равновероятен. ^[48] Это случайное блуждание имеет гораздо более сильные свойства локализации.

Существует ряд интересных моделей случайных путей, в которых каждый шаг зависит от прошлого сложным образом. Все они более сложны для аналитического решения, чем обычное случайное блуждание; тем не менее, поведение любой модели случайного блуждания может быть получено с помощью компьютеров. Вот некоторые примеры:

• Самоизбегающая прогулка . ^[49]

Самоизбегающий путь длины n на является случайным n -шаговым путем, который начинается в начале координат, совершает переходы только между соседними сайтами в , никогда не посещает сайт повторно и выбирается равномерно среди всех таких путей. В двух измерениях из-за самозахвата типичный самоизбегающий путь очень короткий, ^[50] тогда как в более высоком измерении он растет за пределы всех границ. Эта модель часто использовалась в физике полимеров (с 1960-х годов).${\displaystyle \mathbb {Z} ^{d}}$${\displaystyle \mathbb {Z} ^{d}}$

• Случайное блуждание со стертыми петлями . ^{[51] [52]}
• Усиленное случайное блуждание. ^[53]
• Процесс разведки. ^{[ необходима цитата ]}
• Случайное блуждание с несколькими агентами. ^[54]

Случайное блуждание, выбранное для максимизации скорости энтропии , имеет гораздо более сильные свойства локализации.

Случайные блуждания, где направление движения в один момент времени коррелирует с направлением движения в следующий момент времени. Используется для моделирования движений животных. ^{[55] [56]}

• Случайное блуждание с ветвлениями
• Броуновское движение
• Закон повторного логарифма
• Полет Леви
• Гипотеза о полете Леви в поисках пищи
• Случайное блуждание со стертыми петлями
• Максимальная энтропия случайного блуждания
• Прогулка с самоизбеганием
• Единичный корень

• Aldous, David ; Fill, James Allen (2002). Обратимые цепи Маркова и случайные блуждания на графах. Архивировано из оригинала 27 февраля 2019 г.
• Дойл, Питер Г.; Снелл, Дж. Лори (1984). Случайные блуждания и электрические сети . Математические монографии Каруса. Том 22. Математическая ассоциация Америки . arXiv : math.PR/0001057 . ISBN 978-0-88385-024-4. МР  0920811.
• Феллер, Уильям (1968), Введение в теорию вероятностей и ее приложения (том 1). ISBN 0-471-25708-7 
• Хьюз, Барри Д. (1996), Случайные блуждания и случайные среды , Oxford University Press. ISBN 0-19-853789-1 
• Норрис, Джеймс (1998), Цепи Маркова , Cambridge University Press. ISBN 0-521-63396-6 
• Полиа Г. (1921), «Über eine Aufgabe der Wahrscheinlichkeitsrechnung betreffend die Irrfahrt im Strassennetz». Архивировано 4 марта 2016 г. в Wayback Machine , Mathematische Annalen , 84 (1–2): 149–160, март 1921 г.
• Ревес, Пал (2013), Случайное блуждание в случайных и неслучайных средах (третье издание) , World Scientific Pub Co. ISBN 978-981-4447-50-8 
• Sunada, Toshikazu (2012). Топологическая кристаллография: с видом на дискретный геометрический анализ . Обзоры и руководства по прикладным математическим наукам. Том 6. Springer. ISBN 978-4-431-54177-6.
• Вайс Г. Аспекты и приложения случайного блуждания , Северная Голландия, 1994.
• Woess, Wolfgang (2000), Случайные блуждания по бесконечным графам и группам , Cambridge tracts in Mathematics 138, Cambridge University Press. ISBN 0-521-55292-3 

• Константы случайного блуждания Пойи
• Случайный обход в Java Applet Архивировано 31 августа 2007 г. на Wayback Machine
• Квантовое случайное блуждание
• Гауссовская оценка случайного блуждания
• Модели электронной проводимости с использованием случайных блужданий с максимальной энтропией. Проект демонстраций Wolfram