Электрическая сеть
This article needs additional citations for verification. (March 2016) |
| Articles about |
| Electromagnetism |
|---|
 |
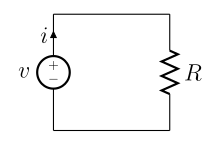
Электрическая сеть — это взаимосвязь электрических компонентов (например, батарей , резисторов , индукторов , конденсаторов , переключателей , транзисторов ) или модель такой взаимосвязи, состоящая из электрических элементов (например, источников напряжения , источников тока , сопротивлений , индуктивностей , емкостей ). Электрическая цепь — это сеть, состоящая из замкнутого контура, дающего обратный путь для тока. Таким образом, все цепи являются сетями, но не все сети являются контурами (хотя сети без замкнутого контура часто неточно называют «контурами»). Линейные электрические сети, особый тип, состоящий только из источников (напряжения или тока), линейных сосредоточенных элементов (резисторов, конденсаторов, индукторов) и линейных распределенных элементов (линий передачи), обладают тем свойством, что сигналы линейно накладываются друг на друга . Таким образом, их легче анализировать, используя мощные методы частотной области , такие как преобразования Лапласа , для определения отклика постоянного тока , отклика переменного тока и переходного отклика .
Резистивная сеть — это сеть, содержащая только резисторы и идеальные источники тока и напряжения. Анализ резистивных сетей менее сложен, чем анализ сетей, содержащих конденсаторы и индукторы. Если источники являются постоянными ( DC ) источниками, результатом является сеть постоянного тока. Эффективное сопротивление и свойства распределения тока произвольных резистивных сетей могут быть смоделированы в терминах их графических мер и геометрических свойств. [1]
Сеть, которая содержит активные электронные компоненты, называется электронной схемой . Такие сети, как правило, нелинейны и требуют более сложных инструментов проектирования и анализа.
Классификация
Пассивностью
Активная сеть содержит по крайней мере один источник напряжения или тока , который может поставлять энергию в сеть неограниченное время. Пассивная сеть не содержит активного источника.
Активная сеть содержит один или несколько источников электродвижущей силы . Практическими примерами таких источников являются аккумулятор или генератор . Активные элементы могут подавать питание в цепь, обеспечивать усиление мощности и управлять током в цепи.
Пассивные сети не содержат никаких источников электродвижущей силы. Они состоят из пассивных элементов, таких как резисторы и конденсаторы.
По линейности
Сеть линейна, если ее сигналы подчиняются принципу суперпозиции ; в противном случае она нелинейна. Пассивные сети обычно считаются линейными, но есть исключения. Например, индуктор с железным сердечником может быть приведен в насыщение , если по нему подать достаточно большой ток. В этой области поведение индуктора очень нелинейно.
По комковатости
Дискретные пассивные компоненты (резисторы, конденсаторы и индукторы) называются сосредоточенными элементами, поскольку предполагается, что все их, соответственно, сопротивление, емкость и индуктивность расположены («сосредоточены») в одном месте. Такая философия проектирования называется моделью сосредоточенных элементов , а сети, спроектированные таким образом, называются схемами с сосредоточенными элементами . Это традиционный подход к проектированию схем. На достаточно высоких частотах или для достаточно длинных цепей (например, линий электропередачи ) сосредоточенное предположение больше не выполняется, поскольку на размеры компонента приходится значительная часть длины волны . Для таких случаев необходима новая модель проектирования, называемая моделью распределенных элементов . Сети, спроектированные по этой модели, называются схемами с распределенными элементами .
Схема с распределенными элементами, включающая некоторые сосредоточенные компоненты, называется полусосредоточенной конструкцией. Примером полусосредоточенной схемы является гребенчатый фильтр .
Классификация источников
Источники можно разделить на независимые и зависимые.
Независимый
Идеальный независимый источник поддерживает одинаковое напряжение или ток независимо от других элементов, присутствующих в цепи. Его значение либо постоянно (DC), либо синусоидально (AC). Сила напряжения или тока не изменяется при любых изменениях в подключенной сети.
Зависимый
Зависимые источники зависят от конкретного элемента цепи, обеспечивающего подачу мощности, напряжения или тока в зависимости от типа источника.
Применение законов электричества
Ко всем линейным резистивным сетям применим ряд законов электротехники. К ним относятся:
- Закон токов Кирхгофа : сумма всех токов, входящих в узел, равна сумме всех токов, выходящих из узла.
- Закон напряжения Кирхгофа : направленная сумма разностей электрических потенциалов вокруг контура должна быть равна нулю.
- Закон Ома : напряжение на резисторе равно произведению сопротивления на ток, протекающий через него.
- Теорема Нортона : Любая сеть источников напряжения или тока и резисторов электрически эквивалентна идеальному источнику тока, подключенному параллельно с одним резистором.
- Теорема Тевенена : Любая сеть источников напряжения или тока и резисторов электрически эквивалентна одному источнику напряжения, соединенному последовательно с одним резистором.
- Теорема суперпозиции : в линейной сети с несколькими независимыми источниками отклик в определенной ветви, когда все источники действуют одновременно, равен линейной сумме отдельных откликов, рассчитанных путем взятия по одному независимому источнику за раз.
Применение этих законов приводит к набору одновременных уравнений, которые можно решить либо алгебраически, либо численно. Законы, как правило, можно распространить на сети, содержащие реактивные сопротивления . Их нельзя использовать в сетях, содержащих нелинейные или изменяющиеся во времени компоненты.
Методы проектирования
| Линейный сетевой анализ | |
|---|---|
| Элементы | |
| Компоненты | |
| Последовательные и параллельные цепи | |
| Преобразования импеданса | |
| Теоремы о генераторах | Сетевые теоремы |
| Методы сетевого анализа | |
| Параметры двух портов | |
Для проектирования любой электрической цепи, как аналоговой , так и цифровой , инженеры-электрики должны уметь прогнозировать напряжения и токи во всех местах цепи. Простые линейные цепи можно анализировать вручную с использованием теории комплексных чисел . В более сложных случаях цепь можно анализировать с помощью специализированных компьютерных программ или методов оценки, таких как кусочно-линейная модель.
Программное обеспечение для моделирования схем, такое как HSPICE (симулятор аналоговых схем) [2] , и такие языки, как VHDL-AMS и verilog-AMS, позволяют инженерам проектировать схемы без затрат времени, средств и риска ошибок, присущих созданию прототипов схем.
Программное обеспечение для моделирования сети
Более сложные схемы можно анализировать численно с помощью такого программного обеспечения, как SPICE или GNUCAP , или символически с помощью такого программного обеспечения, как SapWin .
Линеаризация вокруг рабочей точки
Столкнувшись с новой схемой, программное обеспечение сначала пытается найти решение для устойчивого состояния , то есть такое, в котором все узлы подчиняются закону Кирхгофа для токов , а напряжения на каждом элементе схемы и через него подчиняются уравнениям напряжения/тока, регулирующим этот элемент.
После того, как найдено решение для стационарного состояния, рабочие точки каждого элемента в схеме известны. Для анализа малых сигналов каждый нелинейный элемент может быть линеаризован вокруг своей рабочей точки, чтобы получить оценку малых сигналов напряжений и токов. Это применение закона Ома. Полученная линейная матрица схемы может быть решена с помощью метода исключения Гаусса .
Кусочно-линейная аппроксимация
Программное обеспечение, такое как интерфейс PLECS для Simulink, использует кусочно-линейную аппроксимацию уравнений, управляющих элементами схемы. Схема рассматривается как полностью линейная сеть идеальных диодов . Каждый раз, когда диод переключается из включенного состояния в выключенное или наоборот, конфигурация линейной сети меняется. Добавление большей детализации в аппроксимацию уравнений повышает точность моделирования, но также увеличивает время его выполнения.
Смотрите также
- Цифровая схема
- Земля (электричество)
- Сопротивление
- Нагрузка
- Мемристор
- Напряжение холостого хода
- Короткое замыкание
- Падение напряжения
Представление
Методологии проектирования и анализа
- Анализ сетей (электрические цепи)
- Математические методы в электронике
- Теорема о суперпозиции
- Топология (электроника)
- Анализ сетки
- Фильтр прототипа
Измерение
Аналогии
- Гидравлическая аналогия
- Механико-электрические аналогии
- Аналогия импеданса (аналогия Максвелла)
- Аналогия мобильности (аналогия Файрстоуна)
- Сквозная аналогия (аналогия Трента)
Конкретные топологии
- Мостовая схема
- LC-контур
- RC-цепь
- RL-цепь
- RLC-цепь
- Потенциальный делитель
- Последовательные и параллельные цепи
Ссылки
- ^ Кумар, Анкуш; Видхьядхираджа, Н. С.; Кулкарни, Г. У. (2017). «Распределение тока в проводящих нанопроволочных сетях». Журнал прикладной физики . 122 (4): 045101. Bibcode : 2017JAP...122d5101K. doi : 10.1063/1.4985792.
- ^ "HSPICE" (PDF) . HSpice . Стэнфордский университет, Электротехнический факультет. 1999.