Полет Леви
Полет Леви — это случайное блуждание , в котором длины шагов имеют стабильное распределение [1] , распределение вероятностей с тяжелым хвостом . При определении блуждания в пространстве размерности больше единицы, шаги совершаются в изотропных случайных направлениях. Более поздние исследователи расширили использование термина «полет Леви», включив в него также случаи, когда случайное блуждание происходит на дискретной сетке, а не на непрерывном пространстве. [2]
Термин «полёт Леви» был придуман в честь Поля Леви Бенуа Мандельбротом [ 3] , который использовал его для одного конкретного определения распределения размеров шагов. Он использовал термин « полёт Коши» для случая, когда распределение размеров шагов является распределением Коши [4], и « полёт Рэлея» для случая, когда распределение является нормальным распределением [5] (что не является примером распределения вероятностей с тяжёлым хвостом).
Частный случай, для которого Мандельброт использовал термин «полет Леви» [3], определяется функцией выживания распределения размеров шагов, U , которая [6]
Здесь D — параметр, связанный с фрактальной размерностью , а распределение является частным случаем распределения Парето .
Характеристики
Полеты Леви по построению являются марковскими процессами . Для общих распределений размера шага, удовлетворяющих степенному условию, расстояние от начала случайного блуждания стремится после большого числа шагов к устойчивому распределению благодаря обобщенной центральной предельной теореме , что позволяет моделировать многие процессы с использованием полетов Леви.
Плотности вероятности для частиц, совершающих полет Леви, можно смоделировать с помощью обобщенной версии уравнения Фоккера–Планка , которое обычно используется для моделирования броуновского движения . Уравнение требует использования дробных производных . Для длин прыжков, имеющих симметричное распределение вероятностей, уравнение принимает простую форму в терминах дробной производной Рисса . В одном измерении уравнение имеет вид
где γ — константа, близкая к константе диффузии, α — параметр устойчивости [ требуется ссылка ] и f ( x , t ) — потенциал. Производную Рисса можно понять в терминах ее преобразования Фурье .
Это можно легко распространить на несколько измерений.
Другим важным свойством полета Леви является расхождение дисперсий во всех случаях, за исключением α = 2, т.е. броуновского движения. В общем случае дробный момент θ распределения расходится, если α ≤ θ . Кроме того,
Экспоненциальное масштабирование длин шагов придает полетам Леви свойство масштабной инвариантности , [ требуется ссылка ], и они используются для моделирования данных, демонстрирующих кластеризацию. [ требуется ссылка ]
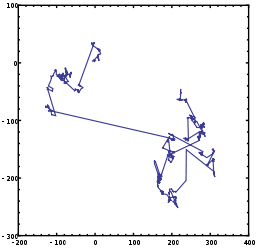

Приложения
Определение полета Леви происходит из математики, связанной с теорией хаоса , и полезно в стохастических измерениях и моделировании случайных или псевдослучайных природных явлений. Примерами являются анализ данных землетрясений , финансовая математика , криптография , анализ сигналов, а также множество приложений в астрономии , биологии и физике .
Было обнаружено, что скачки между состояниями климата, наблюдаемыми в палеоклиматических записях, можно описать как полет Леви или альфа-стабильный процесс [7] Другим применением является гипотеза поиска пищи полетом Леви . Когда акулы и другие океанские хищники не могут найти пищу, они отказываются от броуновского движения , случайного движения, наблюдаемого в закрученных молекулах газа, в пользу полета Леви — смеси длинных траекторий и коротких случайных движений, обнаруженных в турбулентных жидкостях. Исследователи проанализировали более 12 миллионов движений, зарегистрированных в течение 5700 дней у 55 животных, помеченных регистраторами данных, из 14 видов океанских хищников в Атлантическом и Тихом океанах, включая шелковых акул , желтоперого тунца , голубого марлина и меч-рыбу. Данные показали, что полеты Леви, перемежаемые броуновским движением, могут описывать охотничьи модели животных. [8] [9] [10] [11] Птицы и другие животные (включая людей) [12] следуют по траекториям, которые были смоделированы с использованием полета Леви (например, при поиске пищи). [13] Примером животного, в частности жука, который использует модели полета Леви, является Pterostichus melanarius . Когда жуки голодны и пищи мало, они избегают искать добычу в местах, которые посещали другие особи P. melanarius . Такое поведение оптимально для широко распространенной добычи, которая не всегда может быть полностью потреблена за один раз, например, слизней. [14]
Кроме того, биологический полет, по-видимому, может быть имитирован другими моделями, такими как составные коррелированные случайные блуждания, которые растут в масштабах, сходясь к оптимальным блужданиям Леви. [13] Составные броуновские блуждания могут быть точно настроены на теоретически оптимальные блуждания Леви, но они не так эффективны, как поиск Леви в большинстве типов ландшафтов, что предполагает, что давление отбора для характеристик блужданий Леви более вероятно, чем многомасштабные нормальные диффузионные модели. [15]
Эффективная маршрутизация в сети может быть реализована с помощью соединений, имеющих распределение длины полета Леви с определенными значениями альфа. [2]
Смотрите также
- Аномальная диффузия
- Распределение с толстым хвостом
- Распределение с тяжелым хвостом
- Процесс Леви
- Альфа-стабильное распределение Леви
- Гипотеза о полете Леви в поисках пищи
Примечания
- ^ Чечкин, Алексей В.; Мецлер, Ральф; Клафтер, Джозеф; Гончар, Всеволод Ю. (2008). «Введение в теорию полетов Леви». Аномальный транспорт . С. 129–162. doi :10.1002/9783527622979.ch5. ISBN 9783527622979.
- ^ ab JM Kleinberg (2000). «Навигация в маленьком мире». Nature . 406 (6798): 845. Bibcode :2000Natur.406..845K. doi : 10.1038/35022643 . PMID 10972276.
- ^ аб Мандельброт (1982, стр. 289)
- ^ Мандельброт (1982, стр. 290)
- ^ Мандельброт (1982, стр. 288)
- ^ Мандельброт (1982, стр. 294)
- ^ PD Ditlevsen, «Наблюдение альфа-стабильного шума и бистабильного климатического потенциала в записях ледяного керна», Geophys. Res. Lett 26, 1441-1444, 1999.
- ^ Sims, David W.; Southall, Emily J.; Humphries, Nicolas E.; Hays, Graeme C.; Bradshaw, Corey JA; Pitchford, Jonathan W.; James, Alex; Ahmed, Mohammed Z.; Brierley, Andrew S.; Hindell, Mark A.; Morritt, David; Musyl, Michael K.; Righton, David; Shepard, Emily LC; Wearmouth, Victoria J.; Wilson, Rory P.; Witt, Matthew J.; Metcalfe, Julian D. (2008). «Законы масштабирования поведения морских хищников при поиске». Nature . 451 (7182): 1098–1102. Bibcode :2008Natur.451.1098S. doi :10.1038/nature06518. PMID 18305542. S2CID 4412923.
- ^ Хамфрис, Николас Э.; Кейрос, Нуно; Дайер, Дженнифер Р.М.; Паде, Николас Г.; Музиль, Майкл К.; Шефер, Курт М.; Фуллер, Дэниел В.; Брунншвайлер, Юрг М.; Дойл, Томас К.; Хоутон, Джонатан Д.Р.; Хейс, Грэм К.; Джонс, Кэтрин С.; Нобл, Лесли Р.; Уирмут, Виктория Дж.; Саутхолл, Эмили Дж.; Симс, Дэвид В. (2010). «Экологический контекст объясняет закономерности движения морских хищников по типу Леви и Броуновскому» (PDF) . Nature . 465 (7301): 1066–1069. Bibcode : 2010Natur.465.1066H. doi : 10.1038/nature09116. PMID 20531470. S2CID 4316766.
- ^ Витце, Александра. «У акул есть математические навыки». discovery.com . Получено 22 февраля 2013 г.
- ^ Дейси, Джеймс (11 июня 2010 г.). «Акулы охотятся с помощью полетов Леви». Physicsworld.com . Получено 22 февраля 2013 г.
- ^ Рейнольдс, Гретхен (1 января 2014 г.). «Плавание по нашему миру как у птиц» и некоторые авторы утверждали, что движение пчел. The New York Times .
- ^ ab Sims, David W. ; Reynolds, Andrew M.; Humphries, Nicholas E.; Southall, Emily J.; Wearmouth, Victoria J.; Metcalfe, Brett; Twitchett, Richard J. (29 июля 2014 г.). «Иерархические случайные блуждания в ископаемых следах и происхождение оптимального поведения при поиске». Труды Национальной академии наук . 111 (30): 11073–11078. Bibcode :2014PNAS..11111073S. doi : 10.1073/pnas.1405966111 . ISSN 0027-8424. PMC 4121825 . PMID 25024221.
- ^ Гай, Адам Г.; Бохан, Дэвид А.; Пауэрс, Стивен Дж.; Рейнольдс, Эндрю М. (2008-09-01). «Избегание жужелицами запаха своего вида: механизм возникновения моделей поиска без чешуи». Animal Behaviour . 76 (3): 585–591. doi :10.1016/j.anbehav.2008.04.004. ISSN 0003-3472.
- ^ Хамфрис, NE; Симс, DW (2014). «Оптимальные стратегии добычи пищи: прогулки Леви уравновешивают поиск и эксплуатацию участков в очень широком диапазоне условий» (PDF) . Журнал теоретической биологии . 358 : 179–193. Bibcode :2014JThBi.358..179H. doi :10.1016/j.jtbi.2014.05.032. PMID 24882791.
Ссылки
- Мандельброт, Бенуа Б. (1982). Фрактальная геометрия природы (обновленное и дополненное издание). Нью-Йорк: WH Freeman. ISBN 0-7167-1186-9. OCLC 7876824.
Дальнейшее чтение
- Ченг, З.; Савит, Р. (1987). "Фрактальное и нефрактальное поведение в полетах Леви" (PDF) . Журнал математической физики . 28 (3): 592. Bibcode :1987JMP....28..592C. doi :10.1063/1.527644. hdl : 2027.42/70735 .
- Шлезингер, Майкл Ф.; Клафтер, Джозеф; Зумофен, Герт (декабрь 1999 г.). «Выше, ниже и за пределами броуновского движения» (PDF) . American Journal of Physics . 67 (12): 1253–1259. Bibcode :1999AmJPh..67.1253S. doi :10.1119/1.19112. Архивировано из оригинала (PDF) 28.03.2012.
Внешние ссылки
- Сравнение картин Джексона Поллока с моделью самолета Леви


![{\displaystyle F_{k}\left[{\frac {\partial ^{\alpha }\varphi (x,t)}{\partial |x|^{\alpha }}}\right]=-|k|^{\alpha }F_{k}[\varphi (x,t)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a2991424fe3f2d2284bd5e8c81d1a70845503c83)
