Треугольник Паскаля
В математике треугольник Паскаля — это бесконечный треугольный массив биномиальных коэффициентов , которые играют важную роль в теории вероятностей, комбинаторике и алгебре. В большей части западного мира он назван в честь французского математика Блеза Паскаля , хотя другие математики изучали его за столетия до него в Персии, [1] Индии, [2] Китае, Германии и Италии. [3]
Строки треугольника Паскаля традиционно нумеруются, начиная со строки сверху (0-я строка). Элементы в каждой строке нумеруются слева, начиная с и обычно располагаются в шахматном порядке относительно чисел в соседних строках. Треугольник может быть построен следующим образом: в строке 0 (самой верхней строке) есть уникальная ненулевая запись 1. Каждая запись каждой последующей строки строится путем сложения числа выше и слева с числом выше и справа, при этом пустые записи рассматриваются как 0. Например, начальный номер строки 1 (или любой другой строки) равен 1 (сумма 0 и 1), тогда как числа 1 и 3 в строке 3 складываются, чтобы получить число 4 в строке 4.
Формула

В th строке треугольника Паскаля th запись обозначается , произносится как " n choose k ". Например, самая верхняя запись - . С этой нотацией конструкция предыдущего абзаца может быть записана как
для любого положительного целого числа и любого целого числа . [4] Эта повторяемость для биномиальных коэффициентов известна как правило Паскаля .
История

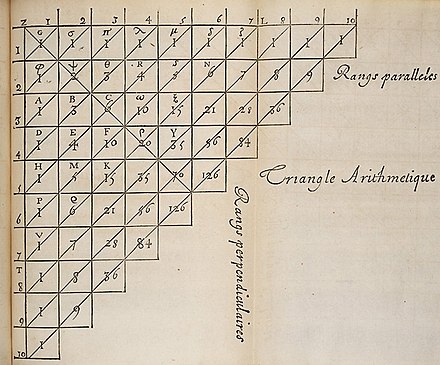
Схема чисел, образующих треугольник Паскаля, была известна задолго до времен Паскаля. Персидский математик Аль-Караджи (953–1029) написал ныне утерянную книгу, которая содержала первую формулировку биномиальных коэффициентов и первое описание треугольника Паскаля. [5] [6] [7] Позднее ее повторил Омар Хайям (1048–1131), другой персидский математик; поэтому треугольник также называют треугольником Хайяма ( مثلث خیام ) в Иране. [8] Было известно несколько теорем, связанных с треугольником, включая биномиальную теорему . Хайям использовал метод нахождения n-ных корней , основанный на биномиальном разложении, и, следовательно, на биномиальных коэффициентах. [1]
Треугольник Паскаля был известен в Китае в начале 11 века благодаря работам китайского математика Цзя Сяня (1010–1070). В 13 веке Ян Хуэй (1238–1298) определил треугольник, и он известен как треугольник Ян Хуэя (杨辉三角;楊輝三角) в Китае. [9]
В Европе треугольник Паскаля впервые появился в « Арифметике » Иордана де Немора (XIII век). [10] Биномиальные коэффициенты были вычислены Герсонидом в начале XIV века с использованием для них мультипликативной формулы. [11] Петрус Апианус (1495–1552) опубликовал полный треугольник на фронтисписе своей книги о деловых вычислениях в 1527 году. [12] Михаэль Штифель опубликовал часть треугольника (со второго по средний столбец в каждой строке) в 1544 году, описав его как таблицу фигурных чисел . [11] В Италии треугольник Паскаля называют треугольником Тартальи , названным в честь итальянского алгебраиста Тартальи (1500–1577), который опубликовал шесть строк треугольника в 1556 году. [11] Джероламо Кардано также опубликовал треугольник, а также аддитивные и мультипликативные правила его построения в 1570 году. [11]
« Traité du triangle arithmétique » Паскаля был опубликован посмертно в 1665 году. [13] В этом труде Паскаль собрал несколько известных на тот момент результатов о треугольнике и применил их для решения задач по теории вероятностей . Треугольник позже был назван в честь Паскаля Пьером Раймоном де Монмором (1708), который назвал его table de M. Pascal pour les combinaisons (по-французски: таблица сочетаний г-на Паскаля), и Авраамом де Муавром (1730), который назвал его Triangulum Arithmeticum PASCALIANUM (по-латыни: арифметический треугольник Паскаля), что стало основой для современного западного названия. [14]
Биномиальные разложения

Треугольник Паскаля определяет коэффициенты, которые возникают в биномиальных разложениях . Например, в разложении коэффициентами являются записи во второй строке треугольника Паскаля: , , .
В общем случае теорема о биноме гласит, что при возведении двучлена в положительную целую степень выражение приобретает вид, где коэффициенты — это в точности числа в строке треугольника Паскаля:
Вся левая диагональ треугольника Паскаля соответствует коэффициенту при в этих биномиальных разложениях, тогда как следующая левая диагональ соответствует коэффициенту при и т.д.
Чтобы увидеть, как биномиальная теорема связана с простой конструкцией треугольника Паскаля, рассмотрим задачу вычисления коэффициентов разложения через соответствующие коэффициенты , где для простоты мы положили . Предположим тогда, что Теперь
Два суммирования можно переиндексировать и объединить, чтобы получить
Таким образом, крайние левые и правые коэффициенты остаются равными 1, и для любого заданного коэффициент члена в многочлене равен , сумме коэффициентов и в предыдущей степени . Это действительно правило нисходящего сложения для построения треугольника Паскаля.
Нетрудно превратить этот аргумент в доказательство (методом математической индукции ) биномиальной теоремы.
Так как , то в разложении общего случая коэффициенты одинаковы.
Интересное следствие биномиальной теоремы получается , если задать обе переменные так, что
Другими словами, сумма элементов в -й строке треугольника Паскаля равна -й степени числа 2. Это эквивалентно утверждению, что число подмножеств -элементного множества равно , как можно увидеть, заметив, что каждый из элементов может быть независимо включен или исключен из данного подмножества.
Комбинации
Второе полезное применение треугольника Паскаля — это расчет комбинаций . Количество комбинаций элементов, взятых за один раз, т.е. количество подмножеств элементов из числа элементов, можно найти с помощью уравнения
- .
Это равно записи в строке треугольника Паскаля. Вместо того, чтобы выполнять мультипликативный расчет, можно просто найти соответствующую запись в треугольнике (построенную путем сложения). Например, предположим, что нужно нанять 3 работников из 7 кандидатов; тогда число возможных вариантов найма равно 7, выбираем 3, запись 3 в строке 7 приведенной выше таблицы, которая равна . [15]
Связь с биномиальным распределением и свертками
При делении на , th строка треугольника Паскаля становится биномиальным распределением в симметричном случае, когда . По центральной предельной теореме это распределение приближается к нормальному распределению с увеличением. Это также можно увидеть, применив формулу Стирлинга к факториалам, участвующим в формуле для комбинаций.
Это связано с операцией дискретной свертки двумя способами. Во-первых, умножение полиномов точно соответствует дискретной свертке, так что многократное свертывание последовательности с собой соответствует взятию степеней , и, следовательно, генерации строк треугольника. Во-вторых, многократное свертывание функции распределения для случайной величины с собой соответствует вычислению функции распределения для суммы n независимых копий этой переменной; это именно та ситуация, к которой применима центральная предельная теорема, и, следовательно, приводит к нормальному распределению в пределе. (Операция многократного взятия свертки чего-либо с собой называется степенью свертки .)
Модели и свойства
Треугольник Паскаля обладает многими свойствами и содержит множество числовых последовательностей.


Ряды
- Сумма элементов одной строки в два раза больше суммы предыдущей строки. Например, строка 0 (самая верхняя строка) имеет значение 1, строка 1 имеет значение 2, строка 2 имеет значение 4 и т. д. Это происходит потому, что каждый элемент в строке производит два элемента в следующей строке: один слева и один справа. Сумма элементов строки равна .
- Взяв произведение элементов в каждой строке, последовательность произведений (последовательность A001142 в OEIS ) связана с основанием натурального логарифма, e . [16] [17] В частности, определим последовательность для всех следующим образом: Тогда отношение последовательных строковых произведений равно , а отношение этих отношений равно Правая часть приведенного выше уравнения принимает форму предельного определения .
- можно найти в треугольнике Паскаля с помощью бесконечного ряда Нилаканта . [18]
- Некоторые числа в треугольнике Паскаля соответствуют числам в треугольнике Лозанича .
- Сумма квадратов элементов строки n равна среднему элементу строки 2 n . Например, 1 2 + 4 2 + 6 2 + 4 2 + 1 2 = 70 . В общем виде,
- В любой четной строке средний член минус член на две позиции левее равняется каталонскому числу , а именно . Например, в строке 4, которая есть 1, 4, 6, 4, 1, мы получаем 3-е каталонское число .
- В строке p , где p — простое число , все члены в этой строке, за исключением единиц, делятся на p . Это можно легко доказать с помощью формулы умножения . Поскольку знаменатель не может иметь простых множителей, равных p , то p остается в числителе после целочисленного деления, делая всю запись кратной p .
- Четность : Чтобы подсчитать нечетные члены в строке n , преобразуйте n в двоичную систему счисления . Пусть x будет числом единиц в двоичном представлении. Тогда число нечетных членов будет 2 x . Эти числа являются значениями в последовательности Гулда . [19]
- Каждая запись в строке 2 n − 1, n ≥ 0, является нечетной. [20]
- Полярность : когда элементы строки треугольника Паскаля попеременно складываются и вычитаются, результат равен 0. Например, строка 6 — это 1, 6, 15, 20, 15, 6, 1, поэтому формула имеет вид 1 − 6 + 15 − 20 + 15 − 6 + 1 = 0.
Диагонали

Диагонали треугольника Паскаля содержат фигурные числа симплексов:
- Диагонали, проходящие вдоль левого и правого краев, содержат только единицы.
- Диагонали рядом с диагоналями края содержат натуральные числа по порядку. Числа одномерного симплекса увеличиваются на 1 по мере того, как отрезки линии расширяются до следующего целого числа вдоль числовой оси.
- Двигаясь внутрь, следующая пара диагоналей содержит треугольные числа по порядку.
- Следующая пара диагоналей содержит тетраэдрические числа по порядку, а следующая пара дает пентатопные числа .
Симметрия треугольника подразумевает, что n- е d-мерное число равно d - му n -мерному числу.
Альтернативная формула, не включающая рекурсию, — это где n ( d ) — возрастающий факториал .
Геометрический смысл функции P d таков: P d (1) = 1 для всех d . Постройте d - мерный треугольник (трехмерный треугольник - это тетраэдр ), разместив дополнительные точки под начальной точкой, что соответствует P d (1) = 1. Разместите эти точки аналогично размещению чисел в треугольнике Паскаля. Чтобы найти P d ( x ), имейте в общей сложности x точек, составляющих целевую фигуру. Тогда P d ( x ) равно общему количеству точек в фигуре. 0-мерный треугольник - это точка, а 1-мерный треугольник - это просто линия, и поэтому P 0 ( x ) = 1 и P 1 ( x ) = x , что является последовательностью натуральных чисел. Количество точек в каждом слое соответствует P d − 1 ( x ).
Вычисление строки или диагонали отдельно
Существуют простые алгоритмы для вычисления всех элементов в строке или диагонали без вычисления других элементов или факториалов.
Для вычисления строки с элементами начните с . Для каждого последующего элемента значение определяется путем умножения предыдущего значения на дробь с медленно меняющимися числителем и знаменателем:
Например, для вычисления строки 5 дроби равны , , , и , а следовательно, элементы равны , , , и т. д. (Остальные элементы проще всего получить с помощью симметрии.)
Чтобы вычислить диагональ, содержащую элементы, снова начните с и получите последующие элементы путем умножения на определенные дроби:
Например, для вычисления диагонали, начинающейся в , дроби равны , а элементы равны , и т.д. По симметрии эти элементы равны , и т.д.

Общие закономерности и свойства

- Рисунок, полученный путем раскрашивания только нечетных чисел в треугольнике Паскаля, очень похож на фрактал, известный как треугольник Серпинского . Это сходство становится все более точным по мере рассмотрения большего количества строк; в пределе, когда число строк приближается к бесконечности, результирующий рисунок представляет собой треугольник Серпинского, предполагая фиксированный периметр. В более общем смысле, числа могут быть окрашены по-разному в зависимости от того, являются ли они кратными 3, 4 и т. д.; это приводит к другим похожим рисункам.
- Поскольку доля черных чисел стремится к нулю с ростом n , следствием этого является то, что доля нечетных биномиальных коэффициентов стремится к нулю, когда n стремится к бесконечности. [21]
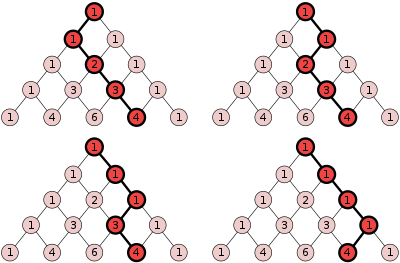
- В треугольной части сетки (как на изображениях ниже) число кратчайших путей сетки от заданного узла до верхнего узла треугольника является соответствующей записью в треугольнике Паскаля. На игровом поле Plinko, имеющем форму треугольника, это распределение должно давать вероятности выигрыша различных призов.
- Если строки треугольника Паскаля выровнены по левому краю, то диагональные полосы (отмечены цветом ниже) в сумме дают числа Фибоначчи .
1 1 1 1 2 1 1 3 3 1 1 4 6 4 1 1 5 10 10 5 1 1 6 15 20 15 6 1 1 7 21 35 35 21 7 1
Построение как матричной экспоненты
Благодаря простоте построения с помощью факториалов можно дать очень простое представление треугольника Паскаля в терминах матричной экспоненты : Треугольник Паскаля — это экспонента матрицы, которая имеет последовательность 1, 2, 3, 4, ... на своей поддиагонали и ноль во всех остальных местах.
Построение алгебры Клиффорда с использованием симплексов
Маркировка элементов каждого n-симплекса соответствует базисным элементам алгебры Клиффорда, используемым в качестве форм в геометрической алгебре, а не матрицам. Распознавание геометрических операций, таких как вращения, позволяет обнаружить алгебраические операции. Так же, как каждая строка, n , начиная с 0, треугольника Паскаля соответствует (n-1) -симплексу, как описано ниже, она также определяет количество именованных базисных форм в n- мерной геометрической алгебре . Биномиальная теорема может быть использована для доказательства геометрической связи, предоставляемой треугольником Паскаля. [22] Это же доказательство можно применить к симплексам, за исключением того, что первый столбец всех единиц должен игнорироваться, тогда как в алгебре они соответствуют действительным числам, , с базисом 1.
Связь с геометрией многогранников
Треугольник Паскаля можно использовать в качестве таблицы поиска для количества элементов (таких как ребра и углы) внутри многогранника (такого как треугольник, тетраэдр, квадрат или куб).
Число элементов симплексов
Давайте начнем с рассмотрения 3-й строки треугольника Паскаля со значениями 1, 3, 3, 1. Двумерный треугольник имеет один двумерный элемент (сам), три одномерных элемента (линии или ребра) и три нульмерных элемента ( вершины или углы). Значение последнего числа (1) объяснить сложнее (но см. ниже). Продолжая наш пример, тетраэдр имеет один трехмерный элемент (сам), четыре двумерных элемента (грани), шесть одномерных элементов (ребра) и четыре нульмерных элемента (вершины). Добавляя последнюю 1 снова, эти значения соответствуют 4-й строке треугольника (1, 4, 6, 4, 1). Линия 1 соответствует точке, а линия 2 соответствует отрезку линии (диаде). Этот шаблон продолжается до произвольно высокоразмерных гипертетраэдров (известных как симплексы ).
Чтобы понять, почему существует эта закономерность, нужно сначала понять, что процесс построения n -симплекса из ( n − 1) -симплекса состоит из простого добавления к последнему новой вершины, расположенной так, чтобы эта новая вершина лежала вне пространства исходного симплекса, и соединения ее со всеми исходными вершинами. В качестве примера рассмотрим случай построения тетраэдра из треугольника, последний из элементов которого пронумерован строкой 3 треугольника Паскаля: 1 грань, 3 ребра и 3 вершины. Чтобы построить тетраэдр из треугольника, расположите новую вершину над плоскостью треугольника и соедините эту вершину со всеми тремя вершинами исходного треугольника.
Число заданного размерного элемента в тетраэдре теперь является суммой двух чисел: во-первых, числа этого элемента, найденного в исходном треугольнике, плюс число новых элементов, каждый из которых построен на элементах на одну размерность меньше из исходного треугольника . Таким образом, в тетраэдре число ячеек (многогранных элементов) равно 0 + 1 = 1 ; число граней равно 1 + 3 = 4 ; число ребер равно 3 + 3 = 6 ; число новых вершин равно 3 + 1 = 4. Этот процесс суммирования числа элементов заданной размерности с числами на одну размерность меньше для получения числа первых, найденных в следующем более высоком симплексе, эквивалентен процессу суммирования двух соседних чисел в строке треугольника Паскаля для получения числа ниже. Таким образом, значение последнего числа (1) в строке треугольника Паскаля становится понятным как представляющее новую вершину, которая должна быть добавлена к симплексу, представленному этой строкой, чтобы получить следующий более высокий симплекс, представленный следующей строкой. Эта новая вершина присоединяется к каждому элементу в исходном симплексе, чтобы получить новый элемент на одно более высокое измерение в новом симплексе, и это является источником паттерна, который, как обнаружено, идентичен тому, который виден в треугольнике Паскаля.
Количество элементов гиперкуба
Похожая закономерность наблюдается в отношении квадратов , в отличие от треугольников. Чтобы найти закономерность, нужно построить аналог треугольника Паскаля, элементы которого являются коэффициентами ( x + 2) номера строки , вместо ( x + 1) номера строки . Есть несколько способов сделать это. Самый простой — начать со строки 0 = 1 и строки 1 = 1, 2. Продолжайте строить аналоговые треугольники в соответствии со следующим правилом:
То есть, выбираем пару чисел в соответствии с правилами треугольника Паскаля, но удваиваем то, что слева, перед сложением. Это дает:
Другой способ создания этого треугольника — начать с треугольника Паскаля и умножить каждую запись на 2k , где k — это позиция в строке данного числа. Например, 2-е значение в строке 4 треугольника Паскаля равно 6 (наклон 1s соответствует нулевой записи в каждой строке). Чтобы получить значение, которое находится в соответствующей позиции в аналоговом треугольнике, умножьте 6 на 2 номер позиции = 6 × 2 2 = 6 × 4 = 24. Теперь, когда аналоговый треугольник построен, количество элементов любого измерения, которые составляют куб произвольного размера (называемый гиперкубом ), можно прочитать из таблицы способом, аналогичным треугольнику Паскаля. Например, количество 2-мерных элементов в 2-мерном кубе (квадрате) равно одному, количество 1-мерных элементов (сторон или линий) равно 4, а количество 0-мерных элементов (точек или вершин) равно 4. Это соответствует 2-й строке таблицы (1, 4, 4). Куб имеет 1 куб, 6 граней, 12 ребер и 8 вершин, что соответствует следующей строке аналогового треугольника (1, 6, 12, 8). Этот шаблон продолжается бесконечно.
Чтобы понять, почему существует эта закономерность, сначала осознайте, что построение n -куба из ( n − 1) -куба выполняется путем простого дублирования исходной фигуры и смещения ее на некоторое расстояние (для обычного n -куба длина ребра) ортогонально пространству исходной фигуры, а затем соединения каждой вершины новой фигуры с соответствующей ей вершиной оригинала. Этот начальный процесс дублирования является причиной того, почему для перечисления размерных элементов n -куба необходимо удвоить первое из пары чисел в строке этого аналога треугольника Паскаля перед суммированием для получения числа ниже. Таким образом, начальное удвоение дает количество «исходных» элементов, которые должны быть найдены в следующем более высоком n -кубе, и, как и прежде, новые элементы строятся на элементах с меньшим измерением (ребра на вершинах, грани на ребрах и т. д.). Опять же, последнее число строки представляет собой количество новых вершин, которые должны быть добавлены для создания следующего более высокого n -куба.
В этом треугольнике сумма элементов строки m равна 3 m . Опять же, если использовать элементы строки 4 в качестве примера: 1 + 8 + 24 + 32 + 16 = 81 , что равно .
Подсчет вершин в кубе по расстоянию
Каждая строка треугольника Паскаля дает количество вершин на каждом расстоянии от фиксированной вершины в n -мерном кубе. Например, в трех измерениях третья строка (1 3 3 1) соответствует обычному трехмерному кубу : фиксируя вершину V , есть одна вершина на расстоянии 0 от V (то есть сама V ), три вершины на расстоянии 1, три вершины на расстоянии √ 2 и одна вершина на расстоянии √ 3 (вершина напротив V ). Вторая строка соответствует квадрату, в то время как строки с большими номерами соответствуют гиперкубам в каждом измерении.
Преобразование Фурье sin(х)н +1/х
Как было сказано ранее, коэффициенты ( x + 1) n являются n-й строкой треугольника. Теперь коэффициенты ( x − 1) n те же самые, за исключением того, что знак меняется с +1 на −1 и обратно. После соответствующей нормализации та же самая последовательность чисел возникает в преобразовании Фурье sin( x ) n +1 / x . Точнее: если n четное, берем действительную часть преобразования, а если n нечетное, берем мнимую часть . Тогда результатом является ступенчатая функция , значения которой (соответствующим образом нормализованные) задаются n- й строкой треугольника с чередующимися знаками. [23] Например, значения ступенчатой функции, которая получается из:
составляют 4-ю строку треугольника, с чередующимися знаками. Это обобщение следующего основного результата (часто используемого в электротехнике ):
является функцией boxcar . [24] Соответствующая строка треугольника — это строка 0, которая состоит только из числа 1.
Если n сравнимо с 2 или 3 mod 4, то знаки начинаются с −1. Фактически, последовательность (нормализованных) первых членов соответствует степеням i , которые циклически повторяют точку пересечения осей с единичной окружностью в комплексной плоскости:
Расширения
Треугольник Паскаля можно расширить вверх, выше 1 в вершине, сохранив аддитивное свойство, но сделать это можно разными способами. [25]
К высшим измерениям
Треугольник Паскаля имеет более высокоразмерные обобщения. Трехмерная версия известна как пирамида Паскаля или тетраэдр Паскаля , в то время как общие версии известны как симплексы Паскаля .
К комплексным числам
Когда функция факториала определена как , треугольник Паскаля может быть расширен за пределы целых чисел до , поскольку является мероморфным всей комплексной плоскости . [26]
К произвольным основаниям
Исаак Ньютон однажды заметил, что первые пять строк треугольника Паскаля, если их читать как цифры целого числа, являются соответствующими степенями одиннадцати. Он утверждал без доказательств, что последующие строки также генерируют степени одиннадцати. [27] В 1964 году Роберт Л. Мортон представил более обобщенный аргумент о том, что каждая строка может быть прочитана как система счисления с основанием, где — гипотетическая конечная строка, или предел , треугольника, а строки — ее частичные произведения. [28] Он доказал, что записи строки , если их интерпретировать непосредственно как разрядное число, соответствуют биномиальному разложению . С тех пор были разработаны более строгие доказательства. [29] [30] Чтобы лучше понять принцип, лежащий в основе этой интерпретации, вот некоторые вещи, которые следует вспомнить о биномах:
- Основание системы счисления в позиционной записи (например, ) — это одномерный многочлен от переменной , где степень переменной -го члена ( начиная с ) равна . Например, .
- Строка соответствует биномиальному разложению . Переменная может быть исключена из разложения, установив . Теперь разложение представляет собой развернутую форму системы счисления с основанием , [31] [32], как показано выше. Таким образом, когда записи строки объединяются и считываются в системе с основанием, они образуют числовой эквивалент . Если для , то теорема верна для с нечетными значениями, дающими отрицательные произведения строк. [33] [34] [35]
При установке основания строки (переменной ) равным единице и десяти, строка становится произведением и , соответственно. Для иллюстрации рассмотрим , что дает произведение строк . Числовое представление формируется путем конкатенации записей строки . Двенадцатая строка обозначает произведение:
с составными цифрами (разделенными знаком ":") в системе счисления с основанием двенадцать. Цифры от до являются составными, поскольку эти записи строк вычисляются до значений, больших или равных двенадцати. Чтобы нормализовать [36] число, просто перенесите префикс первой составной записи, то есть удалите префикс коэффициента от ее самой левой цифры до, но исключая ее самую правую цифру, и используйте арифметику с основанием двенадцать для суммирования удаленного префикса с записью, расположенной непосредственно слева от нее, затем повторите этот процесс, двигаясь влево, пока не будет достигнута самая левая запись. В этом конкретном примере нормализованная строка заканчивается на for all . Самая левая цифра — это for , которая получается путем переноса of в запись . Из этого следует, что длина нормализованного значения равна длине строки, . Целая часть содержит ровно одну цифру, поскольку (количество знаков слева, на которые переместилась десятичная дробь) на единицу меньше длины строки. Ниже приведено нормализованное значение . Составные цифры остаются в значении, поскольку они представляют собой остатки системы счисления, представленные в системе счисления с основанием десять:
Смотрите также
- Машина для производства бобов , «квинконс» Фрэнсиса Гальтона
- Треугольник Белла
- Треугольник Бернулли
- Биномиальное разложение
- Клеточные автоматы
- треугольник Эйлера
- Треугольник Флойда
- Гауссовский биномиальный коэффициент
- Идентичность хоккейной клюшки
- Гармонический треугольник Лейбница
- Кратности элементов в треугольнике Паскаля (гипотеза Зингмастера)
- Матрица Паскаля
- Пирамида Паскаля
- симплекс Паскаля
- Протонный ЯМР , одно из применений треугольника Паскаля
- Теорема о звезде Давида
- Трехчленное разложение
- Треугольник с тремя членами
- Многочлены, вычисляющие суммы степеней арифметических прогрессий
Ссылки
- ^ ab Кулидж, Дж. Л. (1949), «История биномиальной теоремы», The American Mathematical Monthly , 56 (3): 147–157, doi : 10.2307/2305028, JSTOR 2305028, MR 0028222.
- ↑ Морис Винтерниц, История индийской литературы , т. III
- ^ Питер Фокс (1998). Библиотека Кембриджского университета: великие коллекции. Cambridge University Press. стр. 13. ISBN 978-0-521-62647-7.
- ^ Биномиальный коэффициент обычно принимается равным нулю, если k меньше нуля или больше n .
- ^ Селин, Хелайн (2008-03-12). Энциклопедия истории науки, технологий и медицины в не-западных культурах. Springer Science & Business Media. стр. 132. Bibcode :2008ehst.book.....S. ISBN 9781402045592.
- ^ Развитие арабской математики между арифметикой и алгеброй - Р. Рашед "Страница 63"
- ^ Сидоли, Натан; Бруммелен, Глен Ван (2013-10-30). Из Александрии через Багдад: обзоры и исследования древнегреческих и средневековых исламских математических наук в честь Дж. Л. Берггрена. Springer Science & Business Media. стр. 54. ISBN 9783642367366.
- ^ Кеннеди, Э. (1966). Омар Хайям. Учитель математики 1958. Национальный совет учителей математики. С. 140–142. JSTOR i27957284.
- ^ Вайсштейн, Эрик В. (2003). Краткая энциклопедия математики CRC , стр. 2169. ISBN 978-1-58488-347-0 .
- ^ Хьюз, Варнава (1 августа 1989 г.). «Арифметический треугольник Иордана де Немора». История математики . 16 (3): 213–223. дои : 10.1016/0315-0860(89)90018-9 .
- ^ abcd Эдвардс, AWF (2013), «Арифметический треугольник», в Уилсон, Робин; Уоткинс, Джон Дж. (ред.), Комбинаторика: Древняя и современная , Oxford University Press, стр. 166–180.
- ^ Смит, Карл Дж. (2010), Природа математики, Cengage Learning, стр. 10, ISBN 9780538737586.
- ^ Traité du треугольник арифметика, avec quelques autres petits Traitez sur la mesme matière и Gallica
- ^ Фаулер, Дэвид (январь 1996 г.). «Функция биномиального коэффициента». The American Mathematical Monthly . 103 (1): 1–17. doi :10.2307/2975209. JSTOR 2975209.См. в частности стр. 11.
- ^ "Треугольник Паскаля в теории вероятностей". 5010.mathed.usu.edu . Получено 01.06.2023 .
- ^ Brothers, HJ (2012), «Нахождение e в треугольнике Паскаля», Mathematics Magazine , 85 : 51, doi : 10.4169/math.mag.85.1.51, S2CID 218541210.
- ^ Братья, HJ (2012), «Треугольник Паскаля: скрытое хранилище » , The Mathematical Gazette , 96 : 145–148, doi :10.1017/S0025557200004204, S2CID 233356674.
- ^ Фостер, Т. (2014), «Следы Нилаканты в треугольнике Паскаля», Учитель математики , 108 : 247, doi : 10.5951/mathteacher.108.4.0246
- ↑ Файн, Нью-Джерси (1947), «Биномиальные коэффициенты по модулю простого числа», American Mathematical Monthly , 54 (10): 589–592, doi :10.2307/2304500, JSTOR 2304500, MR 0023257. См. в частности теорему 2, которая дает обобщение этого факта для всех простых модулей.
- ^ Хинц, Андреас М. (1992), «Треугольник Паскаля и Ханойская башня», The American Mathematical Monthly , 99 (6): 538–544, doi :10.2307/2324061, JSTOR 2324061, MR 1166003. Хинц приписывает это наблюдение книге Эдуарда Люка 1891 года « Теория чисел» (стр. 420).
- ^ Ян Стюарт, «Как разрезать торт», Oxford University Press, стр. 180
- ^ Уилмот, ГП (2023), Алгебра геометрии
- ^ Похожий пример см., например, в Hore, PJ (1983), «Подавление растворителя в ядерном магнитном резонансе с преобразованием Фурье», Journal of Magnetic Resonance , 55 (2): 283–300, Bibcode : 1983JMagR..55..283H, doi : 10.1016/0022-2364(83)90240-8.
- ^ Карл, Джон Х. (2012), Введение в цифровую обработку сигналов, Elsevier, стр. 110, ISBN 9780323139595.
- ^ Хилтон, П.; и др. (1989). «Расширение биномиальных коэффициентов для сохранения симметрии и шаблона». Симметрия 2. В Международной серии по современной прикладной математике и информатике. Пергам. С. 89–102. doi :10.1016/B978-0-08-037237-2.50013-1. ISBN 9780080372372..
- ^ Хилтон, П.; и др. (1989). «Расширение биномиальных коэффициентов для сохранения симметрии и шаблона». Симметрия 2. В Международной серии по современной прикладной математике и информатике. Pergamon. стр. 100–102. doi :10.1016/B978-0-08-037237-2.50013-1. ISBN 9780080372372..
- ^ Ньютон, Исаак (1736), «Трактат о методе флюксий и бесконечных рядов», Математические труды Исаака Ньютона : 1:31–33,
Но эти в альтернативных областях, которые даны, я заметил, были теми же самыми с фигурами, из которых состоят различные восходящие степени числа 11, а именно
,
,
,
,
, и т. д. то есть, первая 1; вторая 1, 1; третья 1, 2, 1; четвертая 1, 3, 3, 1; пятая 1, 4, 6, 4, 1 и т. д.
.
- ^ Мортон, Роберт Л. (1964), «Треугольник Паскаля и степени 11», Учитель математики , 57 (6): 392–394, doi :10.5951/MT.57.6.0392, JSTOR 27957091.
- ^ Арнольд, Роберт и др. (2004), «Незаконченное дело Ньютона: раскрытие скрытых степеней одиннадцати в треугольнике Паскаля», Труды Дня математики для студентов.
- ^ Ислам, Робиул и др. (2020), Нахождение любой строки треугольника Паскаля, расширяющей концепцию степени 11.
- ^ Winteridge, David J. (1984), «Треугольник Паскаля и степени числа 11», Математика в школе , 13 (1): 12–13, JSTOR 30213884.
- ^ Каллос, Габор (2006), «Обобщение треугольника Паскаля с использованием степеней базовых чисел» (PDF) , Annales Mathématiques , 13 (1): 1–15, doi :10.5802/ambp.211.
- ^ Хилтон, П.; и др. (1989). «Расширение биномиальных коэффициентов для сохранения симметрии и шаблона». Симметрия 2. В Международной серии по современной прикладной математике и информатике. Пергам. С. 89–91. doi :10.1016/B978-0-08-037237-2.50013-1. ISBN 9780080372372..
- ^ Мюллер, Фрэнсис Дж. (1965), «Еще о треугольнике Паскаля и степенях числа 11», Учитель математики , 58 (5): 425–428, doi :10.5951/MT.58.5.0425, JSTOR 27957164.
- ↑ Лоу, Леоне (1966), «Еще больше о треугольнике Паскаля и степенях числа 11», Учитель математики , 59 (5): 461–463, doi :10.5951/MT.59.5.0461, JSTOR 27957385.
- ^ Фьелстад, П. (1991), «Расширение треугольника Паскаля», Компьютеры и математика с приложениями , 21 (9): 3, doi : 10.1016/0898-1221(91)90119-O.
Внешние ссылки
- «Треугольник Паскаля», Энциклопедия математики , EMS Press , 2001 [1994]
- Вайсштейн, Эрик В. «Треугольник Паскаля». MathWorld .
- Старая схема метода семи умножающих квадратов (из «Су Юань Юй Цзянь» Чу Ши-Цзе, 1303 г., изображающая первые девять строк треугольника Паскаля)
- Трактат Паскаля об арифметическом треугольнике (изображения страниц трактата Паскаля, 1654; резюме)


























![{\displaystyle {\begin{aligned}\sum _{i=0}^{n}a_{i}x^{i+1}+\sum _{k=0}^{n}a_{k}x^{k}&=\sum _{k=1}^{n+1}a_{k-1}x^{k}+\sum _{k=0}^{n}a_{k}x^{k}\\[4pt]&=\sum _{k=1}^{n}a_{k-1}x^{k}+a_{n}x^{n+1}+a_{0}x^{0}+\sum _{k=1}^{n}a_{k}x^{k}\\[4pt]&=a_{0}x^{0}+\sum _{k=1}^{n}(a_{k-1}+a_{k})x^{k}+a_{n}x^{n+1}\\[4pt]&=x^{0}+\сумма _{k=1}^{n}(a_{k-1}+a_{k})x^{k}+x^{n+1}.\end{align}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/59f83ea31ae9d776cc212f7a369d19a022b74408)





























































![{\displaystyle {\mathfrak {Re}}\left({\text{Фурье}}\left[{\frac {\sin(x)^{5}}{x}}\right]\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ad6e29379e5b19bf4bb2a63fdc243c4efdad7466)
![{\displaystyle {\mathfrak {Re}}\left({\text{Фурье}}\left[{\frac {\sin(x)^{1}}{x}}\right]\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e746ebf87e79d0988f2c1db9a780b67380b73b42)









































