Пифагорова тройка

Пифагорова тройка состоит из трех положительных целых чисел a , b , и c , таких что a ² + b ² = c ² . Такая тройка обычно записывается ( a , b , c ) , хорошо известный пример - (3, 4, 5) . Если ( a , b , c ) является пифагоровой тройкой, то таковыми являются ( ka , kb , kc ) для любого положительного целого числа k . Треугольник, длины сторон которого являются пифагоровой тройкой, является прямоугольным треугольником и называется пифагоровым треугольником .

Примитивная пифагорова тройка — это тройка, в которой a , b и c взаимно просты ( то есть у них нет общего делителя больше 1). ^[1] Например, (3, 4, 5) является примитивной пифагоровой тройкой, тогда как (6, 8, 10) — нет. Каждая пифагорова тройка может быть масштабирована до уникальной примитивной пифагоровой тройки путем деления ( a , b , c ) на их наибольший общий делитель . И наоборот, каждая пифагорова тройка может быть получена путем умножения элементов примитивной пифагоровой тройки на положительное целое число (то же самое для трех элементов).

Название происходит от теоремы Пифагора , гласящей, что каждый прямоугольный треугольник имеет длины сторон, удовлетворяющие формуле ; таким образом, пифагоровы тройки описывают три целочисленные длины сторон прямоугольного треугольника. Однако прямоугольные треугольники с нецелочисленными сторонами не образуют пифагоровы тройки. Например, треугольник со сторонами и является прямоугольным треугольником, но не является пифагоровой тройкой, потому что квадратный корень из 2 не является целым числом или отношением целых чисел . Более того, и не имеют целого общего кратного, потому что является иррациональным .${\displaystyle а^{2}+b^{2}=c^{2}}$${\displaystyle а=б=1}$${\displaystyle c={\sqrt {2}}}$${\displaystyle (1,1,{\sqrt {2}})}$${\displaystyle 1}$${\displaystyle {\sqrt {2}}}$${\displaystyle {\sqrt {2}}}$

Пифагорейские тройки известны с древних времен. Самая старая известная запись происходит из Plimpton 322 , вавилонской глиняной таблички, датируемой примерно 1800 годом до нашей эры, написанной в шестидесятеричной системе счисления. ^[2]

При поиске целочисленных решений уравнение a ² + b ² = c ² является диофантовым уравнением . Таким образом, пифагоровы тройки являются одними из старейших известных решений нелинейного диофантова уравнения.

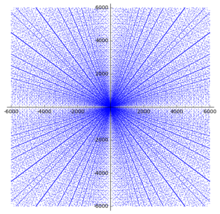
Существует 16 примитивных пифагорейских троек чисел до 100:

Другие малые пифагоровы тройки, такие как (6, 8, 10), не перечислены, поскольку они не являются примитивными; например, (6, 8, 10) кратно (3, 4, 5).

Каждая из этих точек (вместе с их кратными) образует расходящуюся линию на диаграмме рассеяния справа.

Кроме того, вот оставшиеся примитивные пифагорейские тройки чисел до 300:

Формула Евклида ^[3] является фундаментальной формулой для генерации пифагорейских троек по произвольной паре целых чисел m и n , где m > n > 0. Формула утверждает, что целые числа

${\displaystyle a=m^{2}-n^{2},\ \,b=2mn,\ \,c=m^{2}+n^{2}}$

образуют пифагорейскую тройку. Например, дано

${\displaystyle m=2,\ \,n=1}$

сгенерировать примитивную тройку (3,4,5):

${\displaystyle a=2^{2}-1^{2}=3,\ \,b=2\times 2\times 1=4,\ \,c=2^{2}+1^{2}=5.}$

Тройка, сгенерированная формулой Евклида , является примитивной тогда и только тогда, когда m и n взаимно просты и ровно один из них четный. Когда оба m и n нечетны, то a , b и c будут четными, и тройка не будет примитивной; однако деление a , b и c на 2 даст примитивную тройку, когда m и n взаимно просты. ^[4]

Каждая примитивная тройка возникает (после обмена a и b , если a четно) из уникальной пары взаимно простых чисел m , n , одно из которых четно. Из этого следует, что существует бесконечно много примитивных пифагорейских троек. Эта связь a , b и c с m и n из формулы Евклида упоминается в оставшейся части этой статьи.

Несмотря на генерацию всех примитивных троек, формула Евклида не производит все тройки — например, (9, 12, 15) не может быть сгенерирована с использованием целых чисел m и n . Это можно исправить, вставив в формулу дополнительный параметр k . Следующий пример сгенерирует все пифагорейские тройки уникальным образом:

${\displaystyle a=k\cdot (m^{2}-n^{2}),\ \,b=k\cdot (2mn),\ \,c=k\cdot (m^{2}+n^{2})}$

где m , n и k — положительные целые числа, причем m > n , причем m и n взаимно просты и оба не являются нечетными.

То, что эти формулы генерируют пифагоровы тройки, можно проверить, разложив a ² + b ² с помощью элементарной алгебры и проверив, что результат равен c ² . Поскольку каждую пифагорову тройку можно разделить на некоторое целое число k , чтобы получить примитивную тройку, каждую тройку можно сгенерировать уникальным образом, используя формулу с m и n для генерации ее примитивного аналога, а затем умножив на k , как в последнем уравнении.

Выбор m и n из определенных целочисленных последовательностей дает интересные результаты. Например, если m и n — последовательные числа Пелля , a и b будут отличаться на 1. ^[5]

Со времен Евклида было разработано множество формул для генерации троек с определенными свойствами.

То, что выполнение формулы Евклида относительно a, b, c достаточно для того, чтобы треугольник был пифагорейским , очевидно из того факта, что для положительных целых чисел m и n , m > n , a , b и c, заданные формулой, являются положительными целыми числами, и из того факта, что

${\displaystyle a^{2}+b^{2}=(m^{2}-n^{2})^{2}+(2mn)^{2}=(m^{2}+n^{2})^{2}=c^{2}.}$

Доказательство необходимости того , чтобы ^a , b, c выражались формулой Евклида для любой примитивной пифагорейской тройки, выглядит следующим образом. ^[6] Все такие примитивные тройки можно записать как ( a , b , c ) , где a2 + b2 = c2 и a , b , c взаимно просты . Таким образом, ^{a ,} b , c попарно взаимно просты (если бы простое число делило два из них, оно было бы вынуждено делить и третье). Поскольку a и b взаимно просты, по крайней мере одно из них нечетно. Если мы предположим, что a нечетно, то b четно, а c нечетно (если ^бы и a , и b были нечетными, c было бы четным, а c2 было бы кратно 4, в то время как a2 + ^b2 было бы сравнимо с ² по модулю 4 , как нечетный квадрат сравним с 1 по модулю 4).

Из предположим, что a нечетно. Получаем и, следовательно , . Тогда . Так как рационально, то положим его равным в наименьшем выражении. Таким образом , будучи обратной величиной . Тогда решение${\displaystyle а^{2}+b^{2}=c^{2}}$${\displaystyle c^{2}-a^{2}=b^{2}}$${\displaystyle (ca)(c+a)=b^{2}}$${\displaystyle {\tfrac {(c+a)}{b}}={\tfrac {b}{(ca)}}}$${\displaystyle {\tfrac {(c+a)}{b}}}$${\displaystyle {\tfrac {m}{n}}}$${\displaystyle {\tfrac {(ca)}{b}}={\tfrac {n}{m}}}$${\displaystyle {\tfrac {(c+a)}{b}}}$

${\displaystyle {\frac {c}{b}}+{\frac {a}{b}}={\frac {m}{n}},\quad \quad {\frac {c}{b}}-{\frac {a}{b}}={\frac {n}{m}}}$

для и дает${\displaystyle {\tfrac {c}{b}}}$${\displaystyle {\tfrac {a}{b}}}$

${\displaystyle {\frac {c}{b}}={\frac {1}{2}}\left({\frac {m}{n}}+{\frac {n}{m}}\right)={\frac {m^{2}+n^{2}}{2mn}},\quad \quad {\frac {a}{b}}={\frac {1}{2}}\left({\frac {m}{n}}-{\frac {n}{m}}\right)={\frac {m^{2}-n^{2}}{2mn}}.}$

Так как полностью приведено, m и n взаимно просты, и они не могут быть оба четными. Если бы они оба были нечетными, числитель был бы кратен 4 (потому что нечетный квадрат сравним с 1 по модулю 4), а знаменатель 2 mn не был бы кратен 4. Поскольку 4 было бы минимально возможным четным множителем в числителе, а 2 было бы максимально возможным четным множителем в знаменателе, это означало бы, что a четно, несмотря на определение его как нечетного. Таким образом, одно из m и n является нечетным, а другое четным, и числители двух дробей со знаменателем 2 mn нечетны. Таким образом, эти дроби полностью приведены (нечетное простое число, делящее этот знаменатель, делит одно из m и n , но не другое; таким образом, оно не делит m ² ± n ² ). Таким образом, можно приравнять числители к числителям, а знаменатели к знаменателям, что дает формулу Евклида ${\displaystyle {\tfrac {m}{n}}}$${\displaystyle {\tfrac {m^{2}-n^{2}}{2mn}}}$

${\displaystyle a=m^{2}-n^{2},\ \,b=2mn,\ \,c=m^{2}+n^{2}}$где m и n взаимно просты и имеют противоположную четность.

Более длинное, но более банальное доказательство дано в работах Maor (2007) ^[7] и Sierpiński (2003). ^[8] Другое доказательство дано в работе Diophantove equal § Example of Pythagorean triples как пример общего метода, который применим к каждому однородному диофантову уравнению второй степени.

Предположим, что стороны пифагорейского треугольника имеют длины m ² − n ² , 2 mn и m ² + n ² , и предположим, что угол между катетом длиной m ² − n ² и гипотенузой длиной m ² + n ² обозначен как β . Тогда и тригонометрические значения полного угла равны , , и . ^[9]${\displaystyle \tan {\tfrac {\beta }{2}}={\tfrac {n}{m}}}$${\displaystyle \sin {\beta }={\tfrac {2mn}{m^{2}+n^{2}}}}$${\displaystyle \cos {\beta}={\tfrac {m^{2}-n^{2}}{m^{2}+n^{2}}}}$${\displaystyle \tan {\beta }={\tfrac {2mn}{m^{2}-n^{2}}}}$

Следующий вариант формулы Евклида иногда более удобен, так как он более симметричен по m и n (одинаковые условия четности по m и n ).

Если m и n — два нечетных целых числа, причем m > n , то

${\displaystyle a=mn,\quad b={\frac {m^{2}-n^{2}}{2}},\quad c={\frac {m^{2}+n^{2}}{2}}}$

три целых числа, которые образуют пифагорову тройку, которая является примитивной тогда и только тогда, когда m и n взаимно просты. Наоборот, каждая примитивная пифагорова тройка возникает (после обмена a и b , если a четно) из уникальной пары m > n > 0 взаимно простых нечетных целых чисел.

В представлении выше говорится, что все пифагоровы тройки однозначно получаются из формулы Евклида «после замены a на b , если a четно». Формулу Евклида и вариант выше можно объединить следующим образом, чтобы избежать этой замены, что приводит к следующему результату.

Каждая примитивная пифагорова тройка может быть записана однозначно

${\displaystyle a=2\varepsilon mn,\quad b=\varepsilon (m^{2}-n^{2}),\quad c=\varepsilon (m^{2}+n^{2}),}$

где m и n — положительные взаимно простые целые числа, и если m и n — оба нечетные, и в противном случае. Эквивалентно, если a — нечетное, и если a — четное.${\displaystyle \varepsilon = {\frac {1}{2}}}$${\displaystyle \varepsilon =1}$${\displaystyle \varepsilon = {\frac {1}{2}}}$${\displaystyle \varepsilon =1}$

Свойства примитивной пифагорейской тройки ( a , b , c ) , где a < b < c (без указания, какое из чисел a или b является четным, а какое нечетным), включают в себя:

• ${\displaystyle {\tfrac {(ca)(cb)}{2}}}$всегда является полным квадратом. ^[10] Поскольку это только необходимое условие, но не достаточное, его можно использовать для проверки того, не является ли заданная тройка чисел пифагоровой тройкой. Например, тройки {6, 12, 18} и {1, 8, 9} каждая проходит тест на то, что ( c − a )( c − b )/2 является полным квадратом, но ни одна из них не является пифагоровой тройкой.
• Если тройка чисел a , b и c образует примитивную пифагорову тройку, то ( c минус четный катет) и половина ( c минус нечетный катет) являются полными квадратами; однако это не является достаточным условием, так как числа {1, 8, 9} проходят тест на полные квадраты, но не являются пифагоровой тройкой, поскольку 1 ² + 8 ² ≠ 9 ² .
• Максимум один из элементов a , b , c является квадратом. ^[11]
• Площадь пифагорейского треугольника не может быть равна квадрату ^{[12] : стр. 17} или удвоенному квадрату ^{[12] : стр. 21} целого числа.
• Точно один из катетов a , b делится на 2 (является четным ), а гипотенуза c всегда нечетная. ^[13]
• Точно один из a , b делится на 3, но никогда c . ^{[14] [8] : 23–25}
• На 4 делится только одно из чисел a , b ^[8], но не c (потому что c никогда не бывает четным).
• Ровно одно из чисел a , b , c делится на 5. ^[8]
• Наибольшее число, которое всегда делит abc , — 60. ^[15]
• Любое нечетное число вида 2 m +1 , где m — целое число и m >1 , может быть нечетным катетом примитивной пифагоровой тройки. См. раздел «Почти равнобедренные примитивные пифагоровые тройки» ниже. Однако только четные числа, делящиеся на 4, могут быть четным катетом примитивной пифагоровой тройки. Это связано с тем, что формула Евклида для четного катета, приведенная выше, равна 2 mn и один из m или n должен быть четным.
• Гипотенуза c (которая всегда нечетна) является суммой двух квадратов. Это требует, чтобы все ее простые множители были простыми числами вида 4 n + 1 . ^[16] Следовательно, c имеет вид 4 n + 1 . Последовательность возможных чисел гипотенузы для примитивной пифагоровой тройки можно найти по адресу (последовательность A008846 в OEIS ).
• Площадь ( K = ab /2) является конгруэнтным числом ^[17], делящимся на 6.
• В каждом пифагорейском треугольнике радиус вписанной окружности и радиусы трех вневписанных окружностей являются положительными целыми числами. В частности, для примитивной тройки радиус вписанной окружности равен r = n ( m − n ) , а радиусы вневписанных окружностей, противолежащих катетам m ² − n ² , 2mn и гипотенузе m ² + n ^{2 ,} равны соответственно m ( m − n ) , n ( m + n ) и m ( m + n ) . ^[18]
• Как и для любого прямоугольного треугольника, обратная теорема Фалеса гласит, что диаметр описанной окружности равен гипотенузе; следовательно, для примитивных троек диаметр описанной окружности равен m2 + n2 , а радиус описанной окружности равен половине этого значения и, таким образом ^{, является рациональным} , но нецелым числом (поскольку m и n имеют противоположную четность).
• Когда площадь треугольника Пифагора умножается на кривизну его вписанной окружности и 3 вневписанных окружностей, результатом являются четыре положительных целых числа w > x > y > z соответственно. Целые числа − w , x , y , z удовлетворяют уравнению окружности Декарта . ^[19] Эквивалентно, радиус внешнего круга Содди любого прямоугольного треугольника равен его полупериметру. Внешний центр Содди расположен в точке D , где ACBD — прямоугольник, ACB — прямоугольный треугольник, а AB — его гипотенуза. ^{[19] : стр. 6}
• Только две стороны примитивной пифагорейской тройки могут быть одновременно простыми, поскольку по формуле Евклида для создания примитивной пифагорейской тройки один из катетов должен быть составным и четным. ^[20] Однако только одна сторона может быть целым числом совершенной степени , поскольку если бы две стороны были целыми числами совершенной степени с одинаковым показателем, это противоречило бы тому факту, что не существует целочисленных решений диофантова уравнения , при этом , и являются попарно взаимно простыми. ^[21]${\displaystyle p\geq 2}$${\displaystyle p}$ ${\displaystyle x^{2p}\pm y^{2p}=z^{2}}$${\displaystyle x}$${\displaystyle у}$${\displaystyle z}$
• Не существует пифагоровых треугольников, в которых гипотенуза и один катет являются катетами другого пифагорового треугольника; это одна из эквивалентных форм теоремы Ферма о прямоугольном треугольнике . ^{[12] : стр. 14}
• Каждый примитивный пифагорейский треугольник имеет отношение площади K к квадрату полупериметра s , которое является уникальным для него и задается формулой ^[22]

${\displaystyle {\frac {K}{s^{2}}}={\frac {n(mn)}{m(m+n)}}=1-{\frac {c}{s}}.}$

• Ни один примитивный пифагоров треугольник не имеет целочисленной высоты из гипотенузы; то есть каждый примитивный пифагоров треугольник неразложим. ^[23]
• Множество всех примитивных пифагорейских троек естественным образом образует корневое троичное дерево ; см. Дерево примитивных пифагорейских троек .
• Ни один из острых углов пифагорейского треугольника не может быть рациональным числом градусов . ^[24] (Это следует из теоремы Нивена .)

Кроме того, можно гарантировать существование специальных пифагоровских тройок с некоторыми дополнительными свойствами:

• Каждое целое число больше 2, которое не сравнимо с 2 mod 4 (другими словами, каждое целое число больше 2, которое не имеет вида 4 k + 2 ), является частью примитивной пифагорейской тройки. (Если целое число имеет вид 4 k , можно взять n = 1 и m = 2 k в формуле Евклида; если целое число равно 2 k + 1 , можно взять n = k и m = k + 1 .)
• Каждое целое число больше 2 является частью примитивной или непримитивной пифагорейской тройки. Например, целые числа 6, 10, 14 и 18 не являются частью примитивных тройок, но являются частью непримитивных троек (6, 8, 10) , (14, 48, 50) и (18, 80, 82) .
• Существует бесконечно много пифагорейских троек, в которых гипотенуза и самый длинный катет отличаются ровно на единицу. Такие тройки обязательно примитивны и имеют вид (2 n + 1, 2 n ² + 2 n , 2 n ² + 2 n +1) . Это следует из формулы Евклида, замечая, что условие подразумевает, что тройка примитивна и должна проверять ( m ² + n ² ) - 2 mn = 1 . Это подразумевает ( m – n ) ² = 1 , и, таким образом, m = n + 1 . Вышеуказанная форма троек получается, таким образом, заменой m на n + 1 в формуле Евклида.
• Существует бесконечно много примитивных пифагоровых троек, в которых гипотенуза и самый длинный катет отличаются ровно на два. Все они примитивны и получаются подстановкой n = 1 в формулу Евклида. В более общем смысле, для каждого целого числа k > 0 существует бесконечно много примитивных пифагоровых троек, в которых гипотенуза и нечетный катет отличаются на 2 k ² . Они получаются подстановкой n = k в формулу Евклида.
• Существует бесконечно много пифагорейских троек, в которых два катета отличаются ровно на единицу. Например, 20 ² + 21 ² = 29 ² ; они генерируются формулой Евклида, когда является сходящимся к .${\displaystyle {\tfrac {mn}{n}}}$${\displaystyle {\sqrt {2}}}$
• Для каждого положительного целого числа k существует k пифагоровых троек с различными гипотенузами и одинаковой площадью.
• Для каждого положительного целого числа k существует по крайней мере k различных примитивных пифагоровых троек с одинаковым катетом a , где a — некоторое положительное целое число (длина четного катета равна 2 mn , и достаточно выбрать a со многими факторизациями, например a = 4 b , где b — произведение k различных нечетных простых чисел; это дает по крайней мере 2 ^k различных примитивных троек). ^{[8] : 30}
• Для каждого положительного целого числа k существует по крайней мере k различных пифагоровых троек с одинаковой гипотенузой. ^{[8] : 31}
• Если c = p ^e — степень простого числа , то существует примитивная пифагорова тройка a ² + b ² = c ² тогда и только тогда, когда простое число p имеет вид 4 n + 1 ; эта тройка единственна с точностью до замены a на b .
• В более общем случае положительное целое число c является гипотенузой примитивной пифагоровой тройки тогда и только тогда, когда каждый простой множитель c сравним с 1 по модулю 4 ; то есть каждый простой множитель имеет вид 4 n + 1. В этом случае число примитивных пифагоровых троек ( a , b , c ) с a < b равно 2 k ^{−1 ,} где k — число различных простых множителей c . ^[25]
• Существует бесконечно много пифагорейских троек с квадратными числами как для гипотенузы c, так и для суммы катетов a + b . Согласно Ферма, наименьшая такая тройка ^[26] имеет стороны a = 4 565 486 027 761 ; b = 1 061 652 293 520 ; и c = 4 687 298 610 289 . Здесь a + b = 2 372 159 ² и c = 2 165 017 ² . Это генерируется формулой Евклида со значениями параметров m = 2 150 905 и n = 246 792 .
• Существуют не примитивные пифагоровы треугольники с целочисленной высотой из гипотенузы . ^{[27] [28]} Такие пифагоровы треугольники известны как разложимые , поскольку их можно разделить по этой высоте на два отдельных и меньших пифагоровы треугольника. ^[23]

Формула Евклида для пифагоровой тройки

${\displaystyle a=m^{2}-n^{2},\quad b=2mn,\quad c=m^{2}+n^{2}}$

можно понять с точки зрения геометрии рациональных точек на единичной окружности (Траутман, 1998).

Фактически, точка на декартовой плоскости с координатами ( x , y ) принадлежит единичной окружности, если x2 + y2 = 1. ^Точка является рациональной, если ^x и y являются рациональными числами , то есть если существуют взаимно простые целые числа a , b , c, такие, что

${\displaystyle {\biggl (}{\frac {a}{c}}{\biggr )}^{2}+{\biggl (}{\frac {b}{c}}{\biggr )}^{2}=1.}$

Умножив оба члена на c2 , можно увидеть ^, что рациональные точки на окружности находятся во взаимно-однозначном соответствии с примитивными пифагорейскими тройками.

Единичная окружность может быть также определена параметрическим уравнением

${\displaystyle x={\frac {1-t^{2}}{1+t^{2}}}\quad y={\frac {2t}{1+t^{2}}}.}$

Формула Евклида для пифагоровых троек и обратное отношение t = y / ( x + 1) означают, что, за исключением (−1, 0) , точка ( x , y ) на окружности является рациональной тогда и только тогда, когда соответствующее значение t является рациональным числом. Обратите внимание, что t = y / ( x + 1) = b / ( a + c ) = n / m также является тангенсом половины угла , который противолежит стороне треугольника длины b .

Существует соответствие между точками на единичной окружности с рациональными координатами и примитивными пифагорейскими тройками. В этой точке формулы Евклида могут быть выведены либо методами тригонометрии , либо, что эквивалентно, с использованием стереографической проекции .

Для стереографического подхода предположим, что P ′ — это точка на оси x с рациональными координатами

${\displaystyle P'=\left({\frac {m}{n}},0\right).}$

Тогда с помощью элементарной алгебры можно показать, что точка P имеет координаты

${\displaystyle P=\left({\frac {2\left({\frac {m}{n}}\right)}{\left({\frac {m}{n}}\right)^{2}+1}},{\frac {\left({\frac {m}{n}}\right)^{2}-1}{\left({\frac {m}{n}}\right)^{2}+1}}\right)=\left({\frac {2mn}{m^{2}+n^{2}}},{\frac {m^{2}-n^{2}}{m^{2}+n^{2}}}\right).}$

Это устанавливает, что каждая рациональная точка оси x переходит в рациональную точку единичной окружности. Обратное, что каждая рациональная точка единичной окружности происходит из такой точки оси x , следует из применения обратной стереографической проекции. Предположим, что P ( x , y ) — точка единичной окружности с рациональными числами x и y . Тогда точка P ′, полученная стереографической проекцией на ось x, имеет координаты

${\displaystyle \left({\frac {x}{1-y}},0\right)}$

что рационально.

В терминах алгебраической геометрии алгебраическое многообразие рациональных точек на единичной окружности бирационально аффинной прямой над рациональными числами. Таким образом, единичная окружность называется рациональной кривой , и именно этот факт позволяет явно параметризовать (рациональные числа) точек на ней с помощью рациональных функций.

Двумерная решетка — это регулярный массив изолированных точек, где если любая точка выбрана в качестве декартовой точки начала координат (0, 0), то все остальные точки находятся в точке ( x , y ) , где x и y пробегают все положительные и отрицательные целые числа. Любой пифагоров треугольник с тройкой ( a , b , c ) можно нарисовать в двумерной решетке с вершинами в координатах (0, 0) , ( a , 0) и (0, b ) . Количество точек решетки, лежащих строго внутри границ треугольника, определяется выражением   ^[29] для примитивных пифагоровских троек это внутреннее количество решетки равно   Площадь (по теореме Пика, равная на единицу меньше внутреннего количества решетки плюс половина граничного количества решетки) равна    .${\displaystyle {\tfrac {(a-1)(b-1)-\gcd {(a,b)}+1}{2}};}$${\displaystyle {\tfrac {(a-1)(b-1)}{2}}.}$${\displaystyle {\tfrac {ab}{2}}}$

Первое появление двух примитивных пифагорейских троек, имеющих одну и ту же площадь, происходит с треугольниками со сторонами (20, 21, 29), (12, 35, 37) и общей площадью 210 (последовательность A093536 в OEIS ). Первое появление двух примитивных пифагорейских троек, имеющих одно и то же количество внутренних решеток, происходит с (18108, 252685, 253333), (28077, 162964, 165365) и количеством внутренних решеток 2287674594 (последовательность A225760 в OEIS ). Были найдены три примитивные пифагоровые тройки, имеющие одну и ту же площадь: (4485, 5852, 7373) , (3059, 8580, 9109) , (1380, 19019, 19069) с площадью 13123110. До сих пор не было найдено ни одного набора из трех примитивных пифагоровых тройок, имеющих одинаковое количество внутренних решеток.

По формуле Евклида все примитивные пифагоровы тройки могут быть получены из целых чисел и с , нечетными и . Следовательно, существует однозначное соответствие рациональных чисел (в низших членах) примитивным пифагоровам тройкам, где находится в интервале и нечетными.${\displaystyle m}$${\displaystyle n}$${\displaystyle m>n>0}$${\displaystyle m+n}$${\displaystyle \gcd(m,n)=1}$${\displaystyle {\tfrac {n}{m}}}$${\displaystyle (0,1)}$${\displaystyle m+n}$

Обратное отображение из примитивной тройки , где в рациональное число достигается путем изучения двух сумм и . Одна из этих сумм будет квадратом, который можно приравнять , а другая будет удвоенным квадратом, который можно приравнять . Затем можно определить рациональное число .${\displaystyle (a,b,c)}$${\displaystyle c>b>a>0}$${\displaystyle {\tfrac {n}{m}}}$${\displaystyle a+c}$${\displaystyle b+c}$${\displaystyle (m+n)^{2}}$${\displaystyle 2m^{2}}$${\displaystyle {\tfrac {n}{m}}}$

Для того чтобы перечислить примитивные пифагорейские тройки, рациональное число может быть выражено как упорядоченная пара и отображено в целое число с помощью функции спаривания, такой как функция спаривания Кантора . Пример можно увидеть в (последовательность A277557 в OEIS ). Она начинается${\displaystyle (n,m)}$

${\displaystyle 8,18,19,32,33,34,\dots }$и дает рациональные обоснования

${\displaystyle {\tfrac {1}{2}},{\tfrac {2}{3}},{\tfrac {1}{4}},{\tfrac {3}{4}},{\tfrac {2}{5}},{\tfrac {1}{6}},\dots }$они, в свою очередь, генерируют примитивные тройки

${\displaystyle (3,4,5),(5,12,13),(8,15,17),(7,24,25),(20,21,29),(12,35,37),\dots }$

Пифагоровы тройки также можно закодировать в квадратную матрицу вида

${\displaystyle X={\begin{bmatrix}c+b&a\\a&c-b\end{bmatrix}}.}$

Матрица такого вида симметрична . Кроме того , определитель X равен

${\displaystyle \det X=c^{2}-a^{2}-b^{2}\,}$

что равно нулю точно тогда, когда ( a , b , c ) — пифагорова тройка. Если X соответствует пифагорова тройка, то как матрица она должна иметь ранг 1.

Поскольку X симметричен, из результата линейной алгебры следует , что существует вектор-столбец ξ = [ m n ] ^T такой, что внешнее произведение

${\displaystyle X=2{\begin{bmatrix}m\\n\end{bmatrix}}[m\ n]=2\xi \xi ^{T}\,}$

1

выполняется, где T обозначает транспонированную матрицу . Поскольку ξ и -ξ производят одну и ту же пифагорову тройку, вектор ξ можно считать спинором ( для группы Лоренца SO(1, 2)). В абстрактных терминах формула Евклида означает, что каждая примитивная пифагорова тройка может быть записана как внешнее произведение спинора с самим собой с целыми элементами, как в ( 1 ).

Модульная группа Γ — это множество матриц 2×2 с целыми элементами

${\displaystyle A={\begin{bmatrix}\alpha &\beta \\\gamma &\delta \end{bmatrix}}}$

с определителем, равным единице: αδ − βγ = 1. Этот набор образует группу , поскольку обратная матрица из Γ снова находится в Γ, как и произведение двух матриц из Γ. Модулярная группа действует на совокупность всех целочисленных спиноров. Более того, группа транзитивна на совокупность целочисленных спиноров с относительно простыми элементами. Ибо если [ m n ] ^T имеет относительно простые элементы, то

${\displaystyle {\begin{bmatrix}m&-v\\n&u\end{bmatrix}}{\begin{bmatrix}1\\0\end{bmatrix}}={\begin{bmatrix}m\\n\end{bmatrix}}}$

где u и v выбираются (по алгоритму Евклида ) так, что mu + nv = 1 .

Действуя на спинор ξ в ( 1 ), действие Γ переходит в действие на пифагорейских тройках, при условии, что допускаются тройки с возможными отрицательными компонентами. Таким образом, если A является матрицей в Γ , то

${\displaystyle 2(A\xi )(A\xi )^{T}=AXA^{T}\,}$

2

приводит к действию на матрицу X в ( 1 ). Это не дает четко определенного действия на примитивных тройках, поскольку может привести примитивную тройку к импримитивной. На этом этапе (согласно Trautman 1998) удобно называть тройку ( a , b , c ) стандартной , если c > 0 и либо ( a , b , c ) являются взаимно простыми, либо ( a /2, b /2, c /2) являются взаимно простыми с a /2 нечетным. Если спинор [ m n ] ^T имеет относительно простые элементы, то связанная тройка ( a , b , c ), определяемая ( 1 ), является стандартной тройкой. Из этого следует, что действие модулярной группы транзитивно на множестве стандартных троек.

В качестве альтернативы ограничим внимание теми значениями m и n, для которых m нечетно, а n четно. Пусть подгруппа Γ(2) группы Γ будет ядром гомоморфизма групп

${\displaystyle \Gamma =\mathrm {SL} (2,\mathbf {Z} )\to \mathrm {SL} (2,\mathbf {Z} _{2})}$

где SL(2, Z ₂ ) — специальная линейная группа над конечным полем Z ₂ целых чисел по модулю 2 . Тогда Γ(2) — группа унимодулярных преобразований, сохраняющих четность каждого элемента. Таким образом, если первый элемент ξ нечетный, а второй элемент четный, то то же самое верно для A ξ для всех A ∈ Γ(2) . Фактически, при действии ( 2 ) группа Γ(2) действует транзитивно на наборе примитивных пифагорейских троек (Альперин 2005).

Группа Γ(2) является свободной группой , генераторами которой являются матрицы

${\displaystyle U={\begin{bmatrix}1&2\\0&1\end{bmatrix}},\qquad L={\begin{bmatrix}1&0\\2&1\end{bmatrix}}.}$

Следовательно, каждая примитивная пифагорова тройка может быть получена единственным способом как произведение копий матриц U и  L.

Согласно результату Берггрена (1934), все примитивные пифагоровы тройки могут быть получены из треугольника (3, 4, 5) с помощью трех линейных преобразований T ₁ , T ₂ , T ₃ ниже, где a , b , c являются сторонами тройки:

Другими словами, каждая примитивная тройка будет "родительской" для трех дополнительных примитивных тройок. Начиная с начального узла с a = 3 , b = 4 и c = 5 , операция T ₁ создает новую тройку

(3 − (2×4) + (2×5), (2×3) − 4 + (2×5), (2×3) − (2×4) + (3×5)) = (5, 12, 13),

и аналогично T ₂ и T ₃ производят тройки (21, 20, 29) и (15, 8, 17).

Линейные преобразования T ₁ , T ₂ и T ₃ имеют геометрическую интерпретацию на языке квадратичных форм . Они тесно связаны (но не равны) отражениям, порождающим ортогональную группу x ² + y ² − z ² над целыми числами. ^[30]

В качестве альтернативы формулы Евклида можно проанализировать и доказать с помощью целых чисел Гаусса . ^[31] Целые числа Гаусса являются комплексными числами вида α = u + vi , где u и v являются обычными целыми числами , а i является квадратным корнем из отрицательной единицы . Единицами целых чисел Гаусса являются ±1 и ±i. Обычные целые числа называются рациональными целыми числами и обозначаются как « Z ». Целые числа Гаусса обозначаются как Z [ i ] . Правую часть теоремы Пифагора можно разложить на целые числа Гаусса:

${\displaystyle c^{2}=a^{2}+b^{2}=(a+bi){\overline {(a+bi)}}=(a+bi)(a-bi).}$

Примитивная пифагорова тройка — это тройка, в которой a и b взаимно просты , т. е. они не имеют общих простых множителей в целых числах. Для такой тройки либо a , либо b четны, а другой нечетен; из этого следует, что c также нечетен.

Два множителя z  := a + bi и z*  := a − bi примитивной пифагорейской тройки каждый равен квадрату гауссовского целого числа. Это можно доказать, используя свойство, что каждое гауссово целое число может быть однозначно разложено на гауссовы простые числа до единиц . ^[32] (Эта уникальная факторизация следует из того факта, что, грубо говоря, на них можно определить версию алгоритма Евклида .) Доказательство состоит из трех шагов. Во-первых, если a и b не имеют общих простых множителей в целых числах, то они также не имеют общих простых множителей в гауссовых целых числах. (Предположим, что a = gu и b = gv с целыми числами Гаусса g , u и v , причем g не является единицей. Тогда u и v лежат на одной прямой, проходящей через начало координат. Все целые числа Гаусса на такой прямой являются целыми кратными некоторого целого числа Гаусса h . Но тогда целое число gh ≠ ±1 делит как a, так и b .) Во-вторых, отсюда следует, что z и z* также не имеют общих простых множителей в целых числах Гаусса. Иначе говоря, если бы они были, то их общий делитель δ также делил бы z + z* = 2 a и z − z* = 2 ib . Поскольку a и b взаимно просты, это означает, что δ делит  2 = (1 + i)(1 − i) = i(1 − i) ² . Из формулы c ² = zz* следует, что c четно, что противоречит гипотезе о примитивной пифагорейской тройке. В-третьих, поскольку c ² является квадратом, каждое гауссово простое число в его факторизации удваивается, т.е. встречается четное число раз. Поскольку z и z* не имеют общих простых множителей, это удвоение также верно для них. Следовательно, z и z* являются квадратами.

Таким образом, первый множитель можно записать

${\displaystyle a+bi=\varepsilon \left(m+ni\right)^{2},\quad \varepsilon \in \{\pm 1,\pm i\}.}$

Действительная и мнимая части этого уравнения дают две формулы:

${\displaystyle {\begin{cases}\varepsilon =+1,&\quad a=+\left(m^{2}-n^{2}\right),\quad b=+2mn;\\\varepsilon =-1,&\quad a=-\left(m^{2}-n^{2}\right),\quad b=-2mn;\\\varepsilon =+i,&\quad a=-2mn,\quad b=+\left(m^{2}-n^{2}\right);\\\varepsilon =-i,&\quad a=+2mn,\quad b=-\left(m^{2}-n^{2}\right).\end{cases}}}$

Для любой примитивной пифагоровой тройки должны быть целые числа m и n, такие, что эти два уравнения удовлетворяются. Следовательно, каждая пифагорова тройка может быть сгенерирована из некоторого выбора этих целых чисел.

Если мы рассмотрим квадрат целого числа Гаусса, то получим следующую прямую интерпретацию формулы Евклида как представляющей полный квадрат целого числа Гаусса.

${\displaystyle (m+ni)^{2}=(m^{2}-n^{2})+2mni.}$

Используя тот факт, что гауссовы целые числа являются евклидовой областью и что для гауссовского целого числа p всегда является квадратом, можно показать, что пифагорова тройка соответствует квадрату простого гауссова целого числа, если гипотенуза является простым числом.${\displaystyle |p|^{2}}$

Если гауссово целое число не является простым, то оно является произведением двух гауссовских целых чисел p и q с целыми числами и . Поскольку величины умножаются в гауссовских целых числах, произведение должно быть , которое при возведении в квадрат для нахождения пифагоровой тройки должно быть составным. Контрапозитив завершает доказательство.${\displaystyle |p|^{2}}$${\displaystyle |q|^{2}}$${\displaystyle |p||q|}$

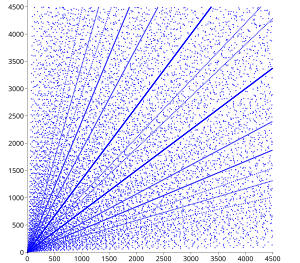
Существует ряд результатов по распределению пифагорейских троек. На диаграмме рассеяния ряд очевидных закономерностей уже очевиден. Всякий раз, когда на диаграмме появляются стороны ( a , b ) примитивной тройки, все целые кратные ( a , b ) также должны появляться на диаграмме, и это свойство создает видимость линий, исходящих из начала координат на диаграмме.

В пределах разброса есть наборы параболических узоров с высокой плотностью точек и всеми их фокусами в начале координат, раскрывающиеся во всех четырех направлениях. Различные параболы пересекаются на осях и, по-видимому, отражаются от оси с углом падения 45 градусов, при этом третья парабола входит перпендикулярно. В пределах этого квадранта каждая дуга с центром в начале координат показывает ту часть параболы, которая лежит между ее вершиной и ее пересечением с ее полуширокой прямой .

Эти закономерности можно объяснить следующим образом. Если — целое число, то ( a , , ) — пифагорова тройка. (На самом деле каждая пифагорова тройка ( a , b , c ) может быть записана таким образом с целым числом n , возможно, после замены a и b , поскольку и a и b не могут быть оба нечетными.) Таким образом, пифагоровы тройки лежат на кривых, заданных , то есть параболами, отраженными относительно оси a , и соответствующими кривыми с a и b , поменянными местами. Если a изменяется для данного n (то есть на данной параболе), целые значения b встречаются относительно часто, если n является квадратом или малым кратным квадрата. Если несколько таких значений оказываются близко друг к другу, соответствующие параболы приблизительно совпадают, и тройки группируются в узкую параболическую полосу. Например, 38 ² = 1444 , 2 × 27 ² = 1458 , 3 × 22 ² = 1452 , 5 × 17 ² = 1445 и 10 × 12 ² = 1440 ; соответствующая параболическая полоса около n ≈ 1450 отчетливо видна на диаграмме рассеяния.${\displaystyle a^{2}/4n}$${\displaystyle |n-a^{2}/4n|}$${\displaystyle n+a^{2}/4n}$${\displaystyle n=(b+c)/2}$${\displaystyle b=|n-a^{2}/4n|}$

Угловые свойства, описанные выше, немедленно следуют из функциональной формы парабол. Параболы отражаются относительно оси a при a = 2 n , а производная b по a в этой точке равна –1; следовательно, угол падения равен 45°. Поскольку кластеры, как и все тройки, повторяются в целых кратных, значение 2 n также соответствует кластеру. Соответствующая парабола пересекает ось b под прямым углом при b = 2 n , и, следовательно, ее отражение при перестановке a и b пересекает ось a под прямым углом при a = 2 n , именно там, где парабола для n отражается относительно оси a . (То же самое, конечно, верно для перестановки a и b .)

Альберт Фесслер и другие дают представление о значении этих парабол в контексте конформных отображений. ^{[33] [34]}

Случай n = 1 более общей конструкции пифагорейских троек известен давно. Прокл в своем комментарии к 47-му предложению первой книги «Начал » Евклида описывает его следующим образом:

Передаются некоторые методы открытия треугольников такого рода, один из которых они относят к Платону, а другой к Пифагору . (Последний) начинает с нечетных чисел. Ибо он делает нечетное число меньшей из сторон вокруг прямого угла; затем он берет его квадрат, вычитает единицу и делает половину разницы большей из сторон вокруг прямого угла; наконец, он прибавляет единицу к этому и таким образом образует оставшуюся сторону, гипотенузу.
... Ибо метод Платона рассуждает от четных чисел. Он берет данное четное число и делает его одной из сторон вокруг прямого угла; затем, делит это число пополам и возводит половину в квадрат, он прибавляет единицу к квадрату, чтобы образовать гипотенузу, и вычитает единицу из квадрата, чтобы образовать другую сторону вокруг прямого угла. ... Таким образом, он образовал тот же самый треугольник, который был получен другим методом.

В форме уравнения это принимает вид:

а — нечетное (Пифагор, ок. 540 г. до н.э.):

${\displaystyle {\text{side }}a:{\text{side }}b={a^{2}-1 \over 2}:{\text{side }}c={a^{2}+1 \over 2}.}$

а — четное (Платон, ок. 380 г. до н.э.):

${\displaystyle {\text{side }}a:{\text{side }}b=\left({a \over 2}\right)^{2}-1:{\text{side }}c=\left({a \over 2}\right)^{2}+1}$

Можно показать, что все пифагоровы тройки могут быть получены с соответствующим перемасштабированием из базовой платоновской последовательности ( ^a , ( a2−1 ) /2 и ( a2 +1)/2 ) ^, разрешив a принимать нецелые рациональные значения. Если заменить a ^{на дробь} m / n в последовательности, результат будет равен «стандартному» генератору тройки (2mn , m2 − n2 , m2 + n2 ) после перемасштабирования. ^Из этого следует, что каждая тройка имеет соответствующее рациональное значение a , которое можно использовать для генерации подобного треугольника (с теми же ^{тремя углами и сторонами в тех же пропорциях ,} что и исходный). Например, платоновский эквивалент (56, 33, 65) генерируется с помощью a = m / n = 7/4 как ( a , ( a2 –1)/2, ( a2 +1)/2) = (56/32, 33/32, 65/32) . Сама последовательность Платона может быть получена ^{[ требуется разъяснение ]} , следуя шагам для «разделения квадрата», описанным ^в Диофанте ^II.VIII .

Уравнение,

${\displaystyle a^{4}+b^{4}+c^{4}+d^{4}=(a+b+c+d)^{4}}$

эквивалентно специальной пифагорейской тройке,

${\displaystyle (a^{2}+ab+b^{2})^{2}+(c^{2}+cd+d^{2})^{2}=((a+b)^{2}+(a+b)(c+d)+(c+d)^{2})^{2}}$

Существует бесконечное число решений этого уравнения, поскольку решение для переменных включает эллиптическую кривую . Маленькие из них:

${\displaystyle a,b,c,d=-2634,955,1770,5400}$

${\displaystyle a,b,c,d=-31764,7590,27385,48150}$

Одним из способов генерации решений является параметризация a, b, c, d в терминах целых чисел m, n, p, q следующим образом: ^[35]${\displaystyle a^{2}+b^{2}=c^{2}+d^{2}}$

${\displaystyle (m^{2}+n^{2})(p^{2}+q^{2})=(mp-nq)^{2}+(np+mq)^{2}=(mp+nq)^{2}+(np-mq)^{2}.}$

Даны два набора пифагорейских троек,

${\displaystyle (a^{2}-b^{2})^{2}+(2ab)^{2}=(a^{2}+b^{2})^{2}}$

${\displaystyle (c^{2}-d^{2})^{2}+(2cd)^{2}=(c^{2}+d^{2})^{2}}$

задача нахождения равных произведений катета, не являющегося гипотенузой , на гипотенузу,

${\displaystyle (a^{2}-b^{2})(a^{2}+b^{2})=(c^{2}-d^{2})(c^{2}+d^{2})}$

легко видеть, что оно эквивалентно уравнению,

${\displaystyle a^{4}-b^{4}=c^{4}-d^{4}}$

и впервые была решена Эйлером как . Поскольку он показал, что это рациональная точка на эллиптической кривой , то существует бесконечное число решений. Фактически, он также нашел параметризацию полинома 7-й степени.${\displaystyle a,b,c,d=133,59,158,134}$

Для случая теоремы Декарта об окружности , где все переменные являются квадратами,

${\displaystyle 2(a^{4}+b^{4}+c^{4}+d^{4})=(a^{2}+b^{2}+c^{2}+d^{2})^{2}}$

Эйлер показал, что это эквивалентно трем одновременным пифагорейским тройкам,

${\displaystyle (2ab)^{2}+(2cd)^{2}=(a^{2}+b^{2}-c^{2}-d^{2})^{2}}$

${\displaystyle (2ac)^{2}+(2bd)^{2}=(a^{2}-b^{2}+c^{2}-d^{2})^{2}}$

${\displaystyle (2ad)^{2}+(2bc)^{2}=(a^{2}-b^{2}-c^{2}+d^{2})^{2}}$

Существует также бесконечное число решений, а для особого случая , когда , уравнение упрощается до вида:${\displaystyle a+b=c}$

${\displaystyle 4(a^{2}+ab+b^{2})=d^{2}}$

с малыми решениями и могут быть решены как бинарные квадратичные формы .${\displaystyle a,b,c,d=3,5,8,14}$

Ни одна пифагорова тройка не является равнобедренной , поскольку отношение гипотенузы к любой другой стороне равно √ 2 , но √ 2 не может быть выражено как отношение двух целых чисел .

Однако существуют прямоугольные треугольники с целыми сторонами, у которых длины сторон, не являющихся гипотенузами, отличаются на единицу, например,

${\displaystyle 3^{2}+4^{2}=5^{2}}$

${\displaystyle 20^{2}+21^{2}=29^{2}}$

и бесконечное множество других. Они могут быть полностью параметризованы как,

${\displaystyle \left({\tfrac {x-1}{2}}\right)^{2}+\left({\tfrac {x+1}{2}}\right)^{2}=y^{2}}$

где { x, y } — решения уравнения Пелля .${\displaystyle x^{2}-2y^{2}=-1}$

Если a , b , c — стороны этого типа примитивной пифагоровой тройки, то решение уравнения Пелля дается рекурсивной формулой

${\displaystyle a_{n}=6a_{n-1}-a_{n-2}+2}$с и${\displaystyle a_{1}=3}$${\displaystyle a_{2}=20}$

${\displaystyle b_{n}=6b_{n-1}-b_{n-2}-2}$с и${\displaystyle b_{1}=4}$${\displaystyle b_{2}=21}$

${\displaystyle c_{n}=6c_{n-1}-c_{n-2}}$с и . ^[36]${\displaystyle c_{1}=5}$${\displaystyle c_{2}=29}$

Эта последовательность примитивных пифагорейских троек образует центральный стебель (ствол) корневого троичного дерева примитивных пифагорейских троек.

Когда более длинная негипотенузная сторона и гипотенуза отличаются на единицу, например, в

${\displaystyle 5^{2}+12^{2}=13^{2}}$

${\displaystyle 7^{2}+24^{2}=25^{2}}$

тогда полное решение для примитивной пифагорейской тройки a , b , c равно

${\displaystyle a=2m+1,\quad b=2m^{2}+2m,\quad c=2m^{2}+2m+1}$

и

${\displaystyle (2m+1)^{2}+(2m^{2}+2m)^{2}=(2m^{2}+2m+1)^{2}}$

где целое число — генерирующий параметр.${\displaystyle m>0}$

Это показывает, что все нечетные числа (больше 1) появляются в этом типе почти равнобедренной примитивной пифагорейской тройки. Эта последовательность примитивных пифагорейских троек образует правый внешний ствол корневого тернарного дерева примитивных пифагорейских троек.

Другим свойством этого типа почти равнобедренной примитивной пифагоровой тройки является то, что стороны связаны таким образом, что

${\displaystyle a^{b}+b^{a}=Kc}$

для некоторого целого числа . Или, другими словами, делится на такое, как в${\displaystyle K}$${\displaystyle a^{b}+b^{a}}$${\displaystyle c}$

${\displaystyle (5^{12}+12^{5})/13=18799189}$. ^[37]

Начиная с 5, каждое второе число Фибоначчи является длиной гипотенузы прямоугольного треугольника с целыми сторонами, или, другими словами, наибольшим числом в пифагоровой тройке, полученным из формулы Последовательность пифагоровых треугольников, полученная из этой формулы, имеет стороны длиной$${\displaystyle (F_{n}F_{n+3})^{2}+(2F_{n+1}F_{n+2})^{2}=F_{2n+3}^{2}.}$$

(3,4,5), (5,12,13), (16,30,34), (39,80,89), ...

Средняя сторона каждого из этих треугольников представляет собой сумму трех сторон предыдущего треугольника. ^[38]

Существует несколько способов обобщения концепции пифагорейских троек.

Выражение

${\displaystyle \left(m_{1}^{2}-m_{2}^{2}-\ldots -m_{n}^{2}\right)^{2}+\sum _{k=2}^{n}(2m_{1}m_{k})^{2}=\left(m_{1}^{2}+\ldots +m_{n}^{2}\right)^{2}}$

является пифагоровским n -кортежем для любого кортежа положительных целых чисел ( m ₁ , ..., m _n ) с m²
₁> м²
₂+ ... + м²
_н. Пифагоров n -кортеж можно сделать примитивным, разделив его на наибольший общий делитель его значений.

Более того, любой примитивный пифагоров n -кортеж a²
₁+ ... + а²
_н= c ² можно найти с помощью этого подхода. Используйте ( m ₁ , ..., m _n ) = ( c + a ₁ , a ₂ , ..., a _n ), чтобы получить пифагоров n -кортеж по приведенной выше формуле и разделите на наибольший общий делитель целых чисел, который равен 2 m ₁ = 2( c + a ₁ ) . Деление на наибольший общий делитель этих значений ( m ₁ , ..., m _n ) дает тот же примитивный пифагоров n -кортеж; и существует взаимно-однозначное соответствие между кортежами взаимно простых положительных целых чисел ( m ₁ , ..., m _n ), удовлетворяющих m²
₁> м²
₂+ ... + м²
_ни примитивные пифагорейские n -кортежи.

Примеры взаимосвязи между взаимно простыми значениями и примитивными пифагорейскими n -кортежами включают в себя: ^[39]${\displaystyle {\vec {m}}}$

${\displaystyle {\begin{aligned}{\vec {m}}=(1)&\leftrightarrow 1^{2}=1^{2}\\{\vec {m}}=(2,1)&\leftrightarrow 3^{2}+4^{2}=5^{2}\\{\vec {m}}=(2,1,1)&\leftrightarrow 1^{2}+2^{2}+2^{2}=3^{2}\\{\vec {m}}=(3,1,1,1)&\leftrightarrow 1^{2}+1^{2}+1^{2}+1^{2}=2^{2}\\{\vec {m}}=(5,1,1,2,3)&\leftrightarrow 1^{2}+1^{2}+1^{2}+2^{2}+3^{2}=4^{2}\\{\vec {m}}=(4,1,1,1,1,2)&\leftrightarrow 1^{2}+1^{2}+1^{2}+1^{2}+1^{2}+2^{2}=3^{2}\\{\vec {m}}=(5,1,1,1,2,2,2)&\leftrightarrow 1^{2}+1^{2}+1^{2}+1^{2}+2^{2}+2^{2}+2^{2}=4^{2}\end{aligned}}}$

Поскольку сумма F ( k , m ) из k последовательных квадратов, начинающихся с m ^{2 ,} определяется формулой, ^[40]

${\displaystyle F(k,m)=km(k-1+m)+{\frac {k(k-1)(2k-1)}{6}}}$

можно найти значения ( k , m ) такие, что F ( k , m ) будет квадратом, например, как у Хиршхорна, где число членов само по себе является квадратом, ^[41]

${\displaystyle m={\tfrac {v^{4}-24v^{2}-25}{48}},\;k=v^{2},\;F(m,k)={\tfrac {v^{5}+47v}{48}}}$

и v ≥ 5 — любое целое число, не делящееся на 2 или 3. Для наименьшего случая v = 5 , следовательно, k = 25 , это приводит к известной задаче Лукаса о складывании пушечных ядер ,

${\displaystyle 0^{2}+1^{2}+2^{2}+\dots +24^{2}=70^{2}}$

факт, связанный с решеткой Лича .

Кроме того, если в пифагоровом n -кортеже ( n ≥ 4 ) все слагаемые являются последовательными, за исключением одного, можно использовать уравнение ^[42]

${\displaystyle F(k,m)+p^{2}=(p+1)^{2}}$

Поскольку вторая степень p сокращается, это уравнение является только линейным и легко решается, как если бы k и m были выбраны так, чтобы p было целым числом, с небольшим примером k = 5 , m = 1 , что дает,${\displaystyle p={\tfrac {F(k,m)-1}{2}}}$

${\displaystyle 1^{2}+2^{2}+3^{2}+4^{2}+5^{2}+27^{2}=28^{2}}$

Таким образом, один из способов генерации пифагорейских n -кортежей заключается в использовании для различных x [ ^43]

${\displaystyle x^{2}+(x+1)^{2}+\cdots +(x+q)^{2}+p^{2}=(p+1)^{2},}$

где q = n –2 и где

${\displaystyle p={\frac {(q+1)x^{2}+q(q+1)x+{\frac {q(q+1)(2q+1)}{6}}-1}{2}}.}$

Обобщением концепции пифагорейских троек является поиск троек положительных целых чисел a , b , и c , таких, что a ⁿ + b ⁿ = c ⁿ , для некоторого n строго большего 2. Пьер де Ферма в 1637 году утверждал, что такой тройки не существует, и это утверждение стало известно как Великая теорема Ферма, поскольку для ее доказательства или опровержения потребовалось больше времени, чем для любой другой гипотезы Ферма. Первое доказательство было дано Эндрю Уайлсом в 1994 году.

Другое обобщение — поиск последовательностей из n + 1 положительных целых чисел, для которых n- я степень последнего члена равна сумме n- х степеней предыдущих членов. Наименьшие последовательности для известных значений n :

• п = 3: {3, 4, 5; 6}.
• n = 4: {30, 120, 272, 315; 353}
• n = 5: {19, 43, 46, 47, 67; 72}
• n = 7: {127, 258, 266, 413, 430, 439, 525; 568}
• n = 8: {90, 223, 478, 524, 748, 1088, 1190, 1324; 1409}

Для случая n = 3 , называемого кубикой Ферма , существует общая формула, дающая все решения.${\displaystyle x^{3}+y^{3}+z^{3}=w^{3},}$

Немного иное обобщение позволяет сумме ( k + 1) n -ных степеней равняться сумме ( n − k ) n -ных степеней. Например:

• ( n = 3 ): 1 ³ + 12 ³ = 9 ³ + 10 ³ , получившее известность благодаря воспоминаниям Харди о разговоре с Рамануджаном о том, что число 1729 является наименьшим числом, которое можно выразить в виде суммы двух кубов двумя различными способами.

Также могут существовать n − 1 положительных целых чисел, чья сумма n -й степени равна n- й степени (хотя, по Великой теореме Ферма , не для n = 3) ; это контрпримеры к гипотезе Эйлера о сумме степеней . Наименьшие известные контрпримеры: ^{[44] [45] [15]}

• n = 4 : (95800, 217519, 414560; 422481)
• n = 5 : (27, 84, 110, 133; 144)

Геронов треугольник обычно определяется как треугольник с целыми сторонами, площадь которого также является целым числом. Длины сторон такого треугольника образуют геронову тройку ( a, b, c ) для a ≤ b ≤ c . Каждая пифагорова тройка является героновой тройкой, потому что по крайней мере один из катетов a , b должен быть четным в пифагоровой тройке, поэтому площадь ab /2 является целым числом. Однако не каждая геронова тройка является пифагоровой тройкой, как показывает пример (4, 13, 15) с площадью 24.

Если ( a , b , c ) — геронова тройка, то и ( ka , kb , kc ) — это любое положительное целое число; ее площадь будет целым числом, которое в k ² раз больше целой площади треугольника ( a , b , c ) . Геронова тройка ( a , b , c ) является примитивной , если a , b , c являются взаимно простыми . (К примитивным пифагоровым тройкам применимо также более сильное утверждение, что они попарно взаимно просты, но к примитивным героновым треугольникам более сильное утверждение не всегда верно, например, к (7, 15, 20) .) Вот несколько простейших примитивных героновых троек, которые не являются пифагоровыми тройками:

(4, 13, 15) с площадью 24

(3, 25, 26) с площадью 36

(7, 15, 20) с площадью 42

(6, 25, 29) с площадью 60

(11, 13, 20) с площадью 66

(13, 14, 15) с площадью 84

(13, 20, 21) с площадью 126

По формуле Герона , дополнительное условие для тройки положительных целых чисел ( a , b , c ) , где a < b < c, чтобы быть героновой, заключается в том, что

( а ² + б ² + с ² ) ² − 2( а ⁴ + б ⁴ + с ⁴ )

или эквивалентно

2( а ² б ² + а ² в ² + б ² в ² ) − ( а ⁴ + б ⁴ + с ⁴ )

быть ненулевым полным квадратом, делящимся на 16.

Примитивные пифагорейские тройки использовались в криптографии в качестве случайных последовательностей и для генерации ключей. ^[46]