Декартова система координат

В геометрии декартова система координат ( UK : / kɑːrˈt iːzjən / , US : / kɑːrˈt iːʒən / ) на плоскости — это система координат , которая однозначно задаёт каждую точку парой действительных чисел, называемых координатами , которые представляют собой расстояния до точки от двух фиксированных перпендикулярно ориентированных линий , называемых координатными линиями , осями координат или просто осями ( множественное число от axis ) системы . Точка , в которой оси пересекаются, называется началом координат и имеет (0, 0) в качестве координат. Направления осей представляют собой ортогональный базис . Комбинация начала координат и базиса образует систему координат, называемую декартовой системой координат .
Аналогично, положение любой точки в трехмерном пространстве может быть задано тремя декартовыми координатами , которые являются знаковыми расстояниями от точки до трех взаимно перпендикулярных плоскостей. В более общем случае, n декартовых координат определяют точку в n -мерном евклидовом пространстве для любого измерения n . Эти координаты являются знаковыми расстояниями от точки до n взаимно перпендикулярных фиксированных гиперплоскостей .

Декартовы координаты названы в честь Рене Декарта , чье изобретение их в 17 веке произвело революцию в математике, позволив выражать проблемы геометрии в терминах алгебры и исчисления . Используя декартову систему координат, геометрические фигуры (такие как кривые ) можно описать уравнениями , включающими координаты точек фигуры. Например, окружность радиусом 2 с центром в начале координат плоскости можно описать как множество всех точек, координаты x и y которых удовлетворяют уравнению x 2 + y 2 = 4 ; площадь , периметр и касательная в любой точке могут быть вычислены из этого уравнения с помощью интегралов и производных таким образом, что их можно применить к любой кривой.
Декартовы координаты являются основой аналитической геометрии и обеспечивают поучительные геометрические интерпретации для многих других разделов математики, таких как линейная алгебра , комплексный анализ , дифференциальная геометрия , многомерное исчисление , теория групп и т. д. Знакомым примером является концепция графика функции . Декартовы координаты также являются важными инструментами для большинства прикладных дисциплин, которые имеют дело с геометрией, включая астрономию , физику , инженерию и многие другие. Они являются наиболее распространенной системой координат, используемой в компьютерной графике , компьютерном геометрическом проектировании и другой обработке данных, связанной с геометрией .
История
Прилагательное «декартов» относится к французскому математику и философу Рене Декарту , который опубликовал эту идею в 1637 году, когда он жил в Нидерландах . Она была независимо открыта Пьером де Ферма , который также работал в трех измерениях, хотя Ферма не опубликовал свое открытие. [1] Французский священнослужитель Николь Орем использовал конструкции, похожие на декартовы координаты, задолго до времен Декарта и Ферма. [2]
И Декарт, и Ферма использовали одну ось в своих трактовках и имели переменную длину, измеряемую относительно этой оси. [3] Концепция использования пары осей была введена позже, после того, как «Геометрия » Декарта была переведена на латынь в 1649 году Франсом ван Схоотеном и его учениками. Эти комментаторы ввели несколько концепций, пытаясь прояснить идеи, содержащиеся в работе Декарта. [4]
Развитие декартовой системы координат сыграло основополагающую роль в развитии исчисления Исааком Ньютоном и Готфридом Вильгельмом Лейбницем . [5] Двухкоординатное описание плоскости позднее было обобщено в концепцию векторных пространств . [6]
Со времен Декарта было разработано много других систем координат, таких как полярные координаты для плоскости, а также сферические и цилиндрические координаты для трехмерного пространства.
Описание
Одно измерение
Аффинная линия с выбранной декартовой системой координат называется числовой прямой . Каждая точка на линии имеет вещественную координату, и каждое вещественное число представляет некоторую точку на линии.
Существует две степени свободы в выборе декартовой системы координат для линии, которые можно задать, выбрав две различные точки вдоль линии и присвоив им два различных действительных числа (чаще всего ноль и единица). Другие точки затем могут быть однозначно назначены числам с помощью линейной интерполяции . Эквивалентно, одна точка может быть назначена определенному действительному числу, например, исходной точке, соответствующей нулю, и ориентированная длина вдоль линии может быть выбрана в качестве единицы, с ориентацией, указывающей соответствие между направлениями вдоль линии и положительными или отрицательными числами. [7] Каждая точка соответствует своему знаковому расстоянию от начала (число с абсолютным значением, равным расстоянию, и знаком + или − , выбранным на основе направления).
Геометрическое преобразование линии может быть представлено функцией действительной переменной , например, перенос линии соответствует сложению, а масштабирование линии соответствует умножению. Любые две декартовы системы координат на линии могут быть связаны друг с другом линейной функцией (функцией вида ), переводящей координату определенной точки в одной системе в ее координату в другой системе. Выбор системы координат для каждой из двух различных линий устанавливает аффинное отображение из одной линии в другую, переводя каждую точку на одной линии в точку на другой линии с той же координатой.
Два измерения
Декартова система координат в двух измерениях (также называемая прямоугольной системой координат или ортогональной системой координат [8] ) определяется упорядоченной парой перпендикулярных линий (осей), единой единицей длины для обеих осей и ориентацией для каждой оси. Точка, где оси встречаются, принимается за начало координат для обеих, таким образом превращая каждую ось в числовую прямую. Для любой точки P , через P проводится линия, перпендикулярная каждой оси, и положение, где она встречается с осью, интерпретируется как число. Два числа в этом выбранном порядке являются декартовыми координатами P . Обратное построение позволяет определить точку P по ее координатам.
Первая и вторая координаты называются абсциссой и ординатой P соответственно ; а точка, где оси пересекаются, называется началом системы координат. Координаты обычно записываются в виде двух чисел в скобках, в указанном порядке, разделенных запятой, как в (3, −10.5) . Таким образом , начало координат имеет координаты (0, 0) , а точки на положительных полуосях, на расстоянии одной единицы от начала координат, имеют координаты (1, 0) и (0, 1) .
В математике, физике и инженерии первая ось обычно определяется или изображается как горизонтальная и ориентированная вправо, а вторая ось — вертикальная и ориентированная вверх. (Однако в некоторых контекстах компьютерной графики ось ординат может быть ориентирована вниз.) Начало координат часто обозначается O , а две координаты часто обозначаются буквами X и Y , или x и y . Тогда оси могут называться осью X и осью Y. Выбор букв происходит из первоначального соглашения, которое заключается в использовании последней части алфавита для обозначения неизвестных значений. Первая часть алфавита использовалась для обозначения известных значений.
Евклидова плоскость с выбранной декартовой системой координат называетсяДекартова плоскость . В декартовой плоскости можно определить канонические представители некоторых геометрических фигур, таких какединичная окружность(с радиусом, равным единице длины, и центром в начале координат),единичный квадрат(диагональ которого имеет конечные точки в(0, 0)и(1, 1)),единичная гиперболаи т. д.
Две оси делят плоскость на четыре прямых угла , называемых квадрантами . Квадранты могут быть названы или пронумерованы различными способами, но квадрант, где все координаты положительны, обычно называется первым квадрантом .
Если координаты точки равны ( x , y ) , то ее расстояния от оси X и от оси Y равны | y | и | x | соответственно; где | · | обозначает абсолютное значение числа.
Три измерения
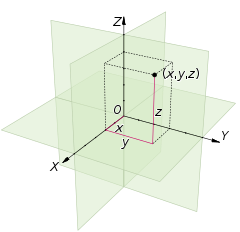
Декартова система координат для трехмерного пространства состоит из упорядоченной тройки линий ( осей ), которые проходят через общую точку ( начало координат ) и попарно перпендикулярны; ориентации для каждой оси; и единой единицы длины для всех трех осей. Как и в двумерном случае, каждая ось становится числовой прямой. Для любой точки P пространства рассматривается плоскость, проходящая через P, перпендикулярная каждой координатной оси, и интерпретируется точка, в которой эта плоскость пересекает ось, как число. Декартовы координаты P — это эти три числа в выбранном порядке. Обратное построение определяет точку P , учитывая ее три координаты.
В качестве альтернативы каждую координату точки P можно принять за расстояние от P до плоскости, определяемой двумя другими осями, причем знак определяется ориентацией соответствующей оси.
Каждая пара осей определяет координатную плоскость . Эти плоскости делят пространство на восемь октантов . Октанты:
Координаты обычно записываются в виде трех чисел (или алгебраических формул), заключенных в скобки и разделенных запятыми, как в (3, −2,5, 1) или ( t , u + v , π /2) . Таким образом, начало координат имеет координаты (0, 0, 0) , а единичные точки на трех осях — это (1, 0, 0) , (0, 1, 0) и (0, 0, 1) .
Стандартные названия координат по трем осям — абсцисса , ордината и аппликата . [9] Координаты часто обозначаются буквами x , y и z . Тогда оси могут называться осью x , осью y и осью z соответственно. Тогда координатные плоскости могут называться плоскостью xy , плоскостью yz и плоскостью xz .
В контексте математики, физики и инженерии первые две оси часто определяются или изображаются как горизонтальные, а третья ось направлена вверх. В этом случае третья координата может называться высотой или altitude . Ориентация обычно выбирается так, чтобы угол в 90 градусов между первой осью и второй осью выглядел против часовой стрелки, если смотреть из точки (0, 0, 1) ; это соглашение обычно называется правилом правой руки .

Более высокие измерения
Поскольку декартовы координаты уникальны и недвусмысленны, точки декартовой плоскости можно отождествить с парами действительных чисел ; то есть с декартовым произведением , где — множество всех действительных чисел. Точно так же точки в любом евклидовом пространстве размерности n можно отождествить с кортежами (списками) из n действительных чисел; то есть с декартовым произведением .
Обобщения
Концепция декартовых координат обобщается, чтобы разрешить оси, которые не перпендикулярны друг другу, и/или разные единицы вдоль каждой оси. В этом случае каждая координата получается путем проецирования точки на одну ось вдоль направления, параллельного другой оси (или, в общем случае, гиперплоскости , определяемой всеми другими осями). В такой косоугольной системе координат вычисления расстояний и углов должны быть изменены по сравнению со стандартными декартовыми системами, и многие стандартные формулы (например, формула Пифагора для расстояния) не выполняются (см. аффинная плоскость ).
Обозначения и соглашения
Декартовы координаты точки обычно записываются в скобках и разделяются запятыми, как в (10, 5) или (3, 5, 7) . Начало координат часто обозначается заглавной буквой O. В аналитической геометрии неизвестные или общие координаты часто обозначаются буквами ( x , y ) на плоскости и ( x , y , z ) в трехмерном пространстве. Этот обычай происходит от соглашения алгебры, в котором буквы в конце алфавита используются для неизвестных значений (например, координат точек во многих геометрических задачах), а буквы в начале — для заданных величин.
Эти общепринятые названия часто используются в других областях, таких как физика и инженерия, хотя могут использоваться и другие буквы. Например, на графике, показывающем, как давление изменяется со временем , координаты графика могут быть обозначены p и t . Каждая ось обычно называется по координате, которая измеряется вдоль нее; так, говорят, что ось x , ось y , ось t и т. д.
Другим распространенным соглашением об именовании координат является использование нижних индексов, как ( x 1 , x 2 , ..., x n ) для n координат в n -мерном пространстве, особенно когда n больше 3 или не указано. Некоторые авторы предпочитают нумерацию ( x 0 , x 1 , ..., x n −1 ). Эти обозначения особенно выгодны в компьютерном программировании : сохраняя координаты точки в виде массива , а не записи , нижний индекс может служить для индексирования координат.
В математических иллюстрациях двумерных декартовых систем первая координата (традиционно называемая абсциссой ) измеряется вдоль горизонтальной оси, ориентированной слева направо. Вторая координата (ордината ) затем измеряется вдоль вертикальной оси, обычно ориентированной снизу вверх. Маленькие дети, изучающие декартову систему, обычно изучают порядок чтения значений, прежде чем закрепить концепции осей x , y и z , начиная с 2D-мнемоники (например, «Идите по коридору, затем поднимитесь по лестнице», что похоже на прямое движение по оси x , затем вертикальное движение по оси y ).
Однако компьютерная графика и обработка изображений часто используют систему координат с осью Y , ориентированной вниз на дисплее компьютера. Эта конвенция возникла в 1960-х годах (или ранее) из того способа, которым изображения изначально хранились в буферах дисплея .
Для трехмерных систем принято изображать плоскость xy горизонтально, с добавленной осью z для представления высоты (положительная вверх). Кроме того, существует соглашение ориентировать ось x по направлению к зрителю, смещенную либо вправо, либо влево. Если диаграмма ( 3D-проекция или 2D-перспективный рисунок ) показывает оси x и y горизонтально и вертикально соответственно, то ось z должна быть показана направленной «из страницы» по направлению к зрителю или камере. На такой 2D-диаграмме 3D-системы координат ось z будет выглядеть как линия или луч, направленный вниз и влево или вниз и вправо, в зависимости от предполагаемой перспективы зрителя или камеры . На любой диаграмме или отображении ориентация трех осей в целом произвольна. Однако ориентация осей относительно друг друга всегда должна соответствовать правилу правой руки , если специально не указано иное. Все законы физики и математики предполагают эту правосторонность, что обеспечивает согласованность.
Для 3D-диаграмм названия «абсцисса» и «ордината» редко используются для x и y соответственно. В таких случаях координата z иногда называется аппликатой . Слова абсцисса , ордината и аппликат иногда используются для обозначения осей координат, а не значений координат. [8]
Квадранты и октанты

Оси двумерной декартовой системы делят плоскость на четыре бесконечные области, называемые квадрантами , [8] каждая из которых ограничена двумя полуосями. Они часто нумеруются от 1-го до 4-го и обозначаются римскими цифрами : I (где обе координаты имеют положительные знаки), II (где абсцисса отрицательна −, а ордината положительна +), III (где и абсцисса, и ордината равны −) и IV (абсцисса +, ордината −). Когда оси рисуются в соответствии с математическим обычаем, нумерация идет против часовой стрелки, начиная с верхнего правого («северо-восточного») квадранта.
Аналогично, трехмерная декартова система определяет разделение пространства на восемь областей или октантов , [8] в соответствии со знаками координат точек. Соглашение, используемое для наименования конкретного октанта, заключается в перечислении его знаков; например, (+ + +) или (− + −) . Обобщением квадранта и октанта на произвольное число измерений является ортант , и применяется похожая система наименования.
Декартовы формулы для плоскости
Расстояние между двумя точками
Евклидово расстояние между двумя точками плоскости с декартовыми координатами равно
Это декартова версия теоремы Пифагора . В трехмерном пространстве расстояние между точками и равно
который может быть получен путем двух последовательных применений теоремы Пифагора. [10]
Евклидовы преобразования
Евклидовы преобразования или евклидовы движения являются ( биективными ) отображениями точек евклидовой плоскости на самих себя, которые сохраняют расстояния между точками. Существует четыре типа этих отображений (также называемых изометриями): переносы , вращения , отражения и скользящие отражения . [11]
Перевод
Перевод набора точек плоскости с сохранением расстояний и направлений между ними эквивалентен добавлению фиксированной пары чисел ( a , b ) к декартовым координатам каждой точки в наборе. То есть, если исходные координаты точки равны ( x , y ) , то после перевода они будут
Вращение
Поворот фигуры против часовой стрелки вокруг начала координат на некоторый угол эквивалентен замене каждой точки с координатами ( x , y ) точкой с координатами ( x' , y' ), где
Таким образом:
Отражение
Если ( x , y ) — декартовы координаты точки, то (− x , y ) — координаты ее отражения относительно второй оси координат (оси y), как если бы эта линия была зеркалом. Аналогично, ( x , − y ) — координаты ее отражения относительно первой оси координат (оси x). В более общем смысле отражение относительно линии, проходящей через начало координат, образующей угол с осью x, эквивалентно замене каждой точки с координатами ( x , y ) точкой с координатами ( x ′, y ′) , где
Таким образом:
Скользить отражение
Скользящее отражение — это композиция отражения поперек линии, за которым следует перенос в направлении этой линии. Видно, что порядок этих операций не имеет значения (перенос может идти первым, а затем — отражение).
Общая матричная форма преобразований
Все аффинные преобразования плоскости можно описать единообразно с помощью матриц. Для этого координаты точки обычно представляются в виде матрицы-столбца Результат применения аффинного преобразования к точке определяется формулой , где — матрица 2×2, а — матрица-столбец. [12] То есть,
Среди аффинных преобразований евклидовы преобразования характеризуются тем, что матрица ортогональна ; то есть ее столбцы являются ортогональными векторами евклидовой нормы один, или, явно, и
Это эквивалентно утверждению, что A , умноженное на транспонированную матрицу, является единичной матрицей . Если эти условия не выполняются, формула описывает более общее аффинное преобразование .
Преобразование является переносом тогда и только тогда, когда A — единичная матрица . Преобразование является вращением вокруг некоторой точки тогда и только тогда, когда A — матрица вращения , что означает, что она ортогональна и
Отражение или скользящее отражение получается, когда,
Предполагая, что переводы не используются (то есть ), преобразования могут быть составлены путем простого умножения соответствующих матриц преобразования. В общем случае полезно использовать расширенную матрицу преобразования; то есть переписать формулу преобразования , где С помощью этого трюка композиция аффинных преобразований получается путем умножения расширенных матриц.
Аффинное преобразование
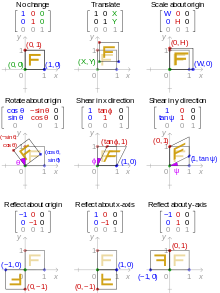
Аффинные преобразования евклидовой плоскости — это преобразования, которые отображают линии в линии, но могут изменять расстояния и углы. Как было сказано в предыдущем разделе, их можно представить с помощью расширенных матриц:
Евклидовы преобразования — это аффинные преобразования, при которых матрица 2×2 является ортогональной .
Расширенная матрица, представляющая композицию двух аффинных преобразований, получается путем умножения их расширенных матриц.
Некоторые аффинные преобразования, не являющиеся евклидовыми преобразованиями, получили специальные названия.
Масштабирование
Примером аффинного преобразования, которое не является евклидовым, является масштабирование. Чтобы сделать фигуру больше или меньше, эквивалентно умножению декартовых координат каждой точки на одно и то же положительное число m . Если ( x , y ) — координаты точки на исходной фигуре, соответствующая точка на масштабированной фигуре имеет координаты
Если m больше 1, число становится больше; если m находится между 0 и 1, оно становится меньше.
Стрижка
Сдвиговая трансформация сдвинет верхнюю часть квадрата вбок, образуя параллелограмм. Горизонтальный сдвиг определяется как:
Стрижку можно также выполнять вертикально:
Ориентация и леворукость
В двух измерениях
Фиксация или выбор оси x определяет направление оси y . А именно, ось y обязательно является перпендикуляром к оси x через точку, обозначенную 0 на оси x . Но есть выбор, какую из двух полупрямых на перпендикуляре обозначить как положительную, а какую как отрицательную. Каждый из этих двух выборов определяет различную ориентацию (также называемую хандардностью ) декартовой плоскости.
Обычный способ ориентации плоскости, при котором положительная ось x направлена вправо, а положительная ось y направлена вверх (при этом ось x является «первой», а ось y — «второй»), считается положительной или стандартной ориентацией, также называемой правой ориентацией.
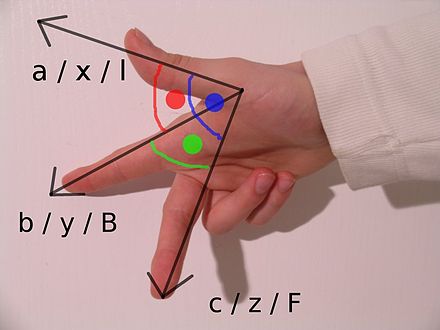
Обычно используемым мнемоническим приемом для определения положительной ориентации является правило правой руки . Помещаем слегка закрытую правую руку на плоскость с большим пальцем, направленным вверх, пальцы указывают от оси x к оси y в положительно ориентированной системе координат.
Другой способ ориентирования плоскости — следовать правилу левой руки , положив левую руку на плоскость большим пальцем вверх.
При направлении большого пальца от начала координат вдоль оси в положительном направлении кривизна пальцев указывает на положительное вращение вдоль этой оси.
Независимо от правила, используемого для ориентации плоскости, поворот системы координат сохранит ориентацию. Переключение любой из осей изменит ориентацию на противоположную, но переключение обеих оставит ориентацию неизменной.
В трех измерениях

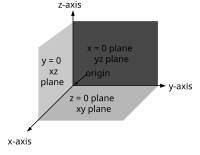
После того, как оси x и y заданы, они определяют линию , вдоль которой должна лежать ось z , но для этой линии возможны две ориентации. Две возможные системы координат, которые получаются в результате, называются «правой» и «левой». [13] Стандартная ориентация, в которой плоскость xy горизонтальна, а ось z направлена вверх (а оси x и y образуют положительно ориентированную двумерную систему координат в плоскости xy, если смотреть сверху плоскости xy ), называется правой или положительной .

Название происходит от правила правой руки . Если указательный палец правой руки направлен вперед, средний палец согнут внутрь под прямым углом к нему, а большой палец расположен под прямым углом к обоим, то три пальца указывают относительную ориентацию осей x , y и z в правосторонней системе. Большой палец указывает на ось x , указательный палец на ось y , а средний палец на ось z . И наоборот, если то же самое сделать с левой рукой, получится левосторонняя система.
На рисунке 7 изображены левая и правая системы координат. Поскольку трехмерный объект представлен на двухмерном экране, возникают искажения и неоднозначность. Ось, направленная вниз (и вправо), также должна указывать на наблюдателя, тогда как «средняя» ось должна указывать от наблюдателя. Красный круг параллелен горизонтальной плоскости xy и указывает на вращение от оси x к оси y (в обоих случаях). Следовательно, красная стрелка проходит перед осью z .
Рисунок 8 — это еще одна попытка изобразить правостороннюю систему координат. Опять же, есть неоднозначность, вызванная проекцией трехмерной системы координат на плоскость. Многие наблюдатели видят Рисунок 8 как «переворачивающийся внутрь и наружу» между выпуклым кубом и вогнутым «углом». Это соответствует двум возможным ориентациям пространства. Видение фигуры как выпуклой дает левостороннюю систему координат. Таким образом, «правильный» способ рассматривать Рисунок 8 — это представить, что ось x направлена на наблюдателя, и таким образом видеть вогнутый угол.
Представление вектора в стандартном базисе
Точка в пространстве в декартовой системе координат может быть также представлена вектором положения , который можно рассматривать как стрелку, направленную от начала системы координат к точке. [14] Если координаты представляют пространственные положения (смещения), то принято представлять вектор от начала до интересующей точки как . В двух измерениях вектор от начала до точки с декартовыми координатами (x, y) можно записать как:
где и являются единичными векторами в направлении оси x и оси y соответственно, обычно называемыми стандартным базисом (в некоторых прикладных областях их также могут называть версорами ). Аналогично, в трех измерениях вектор из начала координат в точку с декартовыми координатами можно записать как: [15]
где и
Не существует естественной интерпретации умножения векторов для получения другого вектора, который работает во всех измерениях, однако есть способ использовать комплексные числа для обеспечения такого умножения. В двумерной декартовой плоскости отождествите точку с координатами ( x , y ) с комплексным числом z = x + iy . Здесь i — мнимая единица и отождествляется с точкой с координатами (0, 1) , поэтому это не единичный вектор в направлении оси x . Поскольку комплексные числа можно умножать, получая другое комплексное число, эта идентификация дает возможность «умножать» векторы. В трехмерном декартовом пространстве похожую идентификацию можно провести с подмножеством кватернионов .
Смотрите также
- Робот с декартовыми координатами
- Горизонтальные и вертикальные
- Диаграмма Джонса , на которой изображены четыре переменные, а не две.
- Ортогональные координаты
- Полярная система координат
- Регулярная сетка
- Сферическая система координат
Цитаты
- ^ Бикс, Роберт А.; Д'Соуза, Гарри Дж. «Аналитическая геометрия». Encyclopaedia Britannica . Получено 6 августа 2017 г.
- ^ Кент и Вуякович 2017, см. здесь
- ^ Кац, Виктор Дж. (2009). История математики: введение (3-е изд.). Бостон: Addison-Wesley. стр. 484. ISBN 978-0-321-38700-4. OCLC 71006826.
- ^ Бертон 2011, стр. 374.
- ^ Берлински 2011
- ^ Акслер 2015, стр. 1
- ^ Рассмотрим два луча или полупрямые, полученные в результате расщепления прямой в начале координат. Одна из полупрямых может быть назначена положительным числам, а другая полупрямая — отрицательным числам.
- ^ abcd "Декартова ортогональная система координат". Энциклопедия математики . Получено 6 августа 2017 г.
- ^ "Декартовы координаты". planetmath.org . Получено 25 августа 2024 г. .
- ^ Хьюз-Халлетт, МакКаллум и Глисон 2013
- ^ Смарт 1998, Гл. 2
- ^ Браннан, Эсплен и Грей 1998, стр. 49
- ^ Антон, Бивенс и Дэвис 2021, стр. 657
- ^ Браннан, Эсплен и Грей 1998, Приложение 2, стр. 377–382.
- ^ Гриффитс 1999
Общие и цитируемые ссылки
- Axler, Sheldon (2015). Линейная алгебра, сделанная правильно. Бакалаврские тексты по математике. Springer. doi :10.1007/978-3-319-11080-6. ISBN 978-3-319-11079-0. Архивировано из оригинала 27 мая 2022 г. . Получено 17 апреля 2022 г. .
- Берлински, Дэвид (2011). Экскурсия по исчислению. Издательская группа Knopf Doubleday. ISBN 9780307789730.
- Бреннан, Дэвид А.; Эсплен, Мэтью Ф.; Грей, Джереми Дж. (1998). Геометрия . Кембридж: Cambridge University Press. ISBN 978-0-521-59787-6.
- Бертон, Дэвид М. (2011). История математики/Введение (7-е изд.). Нью-Йорк: McGraw-Hill. ISBN 978-0-07-338315-6.
- Гриффитс, Дэвид Дж. (1999). Введение в электродинамику . Prentice Hall. ISBN 978-0-13-805326-0.
- Хьюз-Халлетт, Дебора; МакКаллум, Уильям Г.; Глисон, Эндрю М. (2013). Исчисление: одно- и многомерное (6-е изд.). John Wiley & Sons . ISBN 978-0470-88861-2.
- Кент, Александр Дж.; Вуякович, Питер (4 октября 2017 г.). Справочник по картографии и картографии издательства Routledge. Routledge. ISBN 9781317568216.
- Смарт, Джеймс Р. (1998), Современные геометрии (5-е изд.), Пасифик Гроув: Брукс/Коул, ISBN 978-0-534-35188-5
- Антон, Ховард; Бивенс, Ирл К.; Дэвис, Стивен (2021). Исчисление: многомерное. John Wiley & Sons . стр. 657. ISBN 978-1-119-77798-4.
Дальнейшее чтение
- Декарт, Рене (2001). Рассуждение о методе, оптике, геометрии и метеорологии. Перевод Пола Дж. Оскампа (исправленное издание). Индианаполис, Индиана: Hackett Publishing. ISBN 978-0-87220-567-3. OCLC 488633510.
- Корн ГА, Корн ТМ (1961). Справочник по математике для ученых и инженеров (1-е изд.). Нью-Йорк: McGraw-Hill. С. 55–79. LCCN 59-14456. OCLC 19959906.
- Маргенау Х. , Мерфи Г. М. (1956). Математика физики и химии . Нью-Йорк: Д. ван Ностранд. LCCN 55-10911.
- Moon P, Spencer DE (1988). "Прямоугольные координаты (x, y, z)". Справочник по теории поля, включая системы координат, дифференциальные уравнения и их решения (исправленное 2-е, 3-е печатное изд.). Нью-Йорк: Springer-Verlag. С. 9–11 (таблица 1.01). ISBN 978-0-387-18430-2.
- Морзе П.М. , Фешбах Х. (1953). Методы теоретической физики, часть I. Нью-Йорк: McGraw-Hill. ISBN 978-0-07-043316-8. LCCN 52-11515.
- Зауэр Р., Сабо I (1967). Mathematische Hilfsmittel des Ingenieurs . Нью-Йорк: Springer Verlag. LCCN 67-25285.
Внешние ссылки
- Декартова система координат
- Вайсштейн, Эрик В. «Декартовы координаты». MathWorld .
- Преобразователь координат – преобразует полярные, декартовы и сферические координаты
- Координаты точки – интерактивный инструмент для изучения координат точки.
- класс JavaScript с открытым исходным кодом для 2D/3D манипуляции декартовой системой координат













































