Последовательные и параллельные цепи

Двухполюсные компоненты и электрические сети могут быть соединены последовательно или параллельно . Результирующая электрическая сеть будет иметь два вывода и сама может участвовать в последовательной или параллельной топологии . Является ли двухполюсный «объект» электрическим компонентом (например, резистором ) или электрической сетью (например, резисторы последовательно) — вопрос перспективы. В этой статье «компонент» будет использоваться для обозначения двухполюсного «объекта», который участвует в последовательных/параллельных сетях.
Компоненты, соединенные последовательно, соединены вдоль одного "электрического пути", и каждый компонент имеет тот же электрический ток через него, равный току через сеть. Напряжение через сеть равно сумме напряжений через каждый компонент. [1] [2]
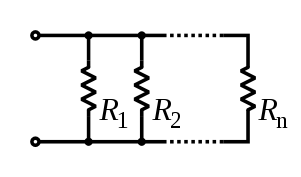
Компоненты, соединенные параллельно, соединены вдоль нескольких путей, и каждый компонент имеет одинаковое напряжение на нем, равное напряжению на сети. Ток через сеть равен сумме токов через каждый компонент.
Два предыдущих утверждения эквивалентны, за исключением того, что меняются местами напряжение и ток .
Цепь, состоящая исключительно из компонентов, соединенных последовательно, называется последовательной цепью ; аналогично, цепь, соединенная полностью параллельно, называется параллельной цепью . Многие цепи можно проанализировать как комбинацию последовательных и параллельных цепей, а также других конфигураций .
В последовательной цепи ток, протекающий через каждый из компонентов, одинаков, а напряжение в цепи представляет собой сумму отдельных падений напряжения на каждом компоненте. [1] В параллельной цепи напряжение на каждом из компонентов одинаково, а общий ток представляет собой сумму токов, протекающих через каждый компонент. [1]
Рассмотрим очень простую схему, состоящую из четырех лампочек и 12-вольтовой автомобильной батареи . Если провод соединяет батарею с одной лампочкой, со следующей лампочкой, со следующей лампочкой, со следующей лампочкой, затем обратно с батареей в одном непрерывном цикле, то лампочки называются последовательными. Если каждая лампочка подключена к батарее в отдельном цикле, то лампочки называются параллельными. Если четыре лампочки соединены последовательно, через них всех протекает одинаковый ток, а падение напряжения составляет 3 вольта на каждой лампочке, чего может быть недостаточно, чтобы они светились. Если лампочки соединены параллельно, токи через лампочки объединяются, образуя ток в батарее, в то время как падение напряжения составляет 12 вольт на каждой лампочке, и они все светятся.
В последовательной цепи каждое устройство должно функционировать, чтобы цепь была замкнутой. Если в последовательной цепи перегорает одна лампочка, вся цепь разрывается. В параллельных цепях каждая лампочка имеет свою собственную цепь, поэтому все лампочки, кроме одной, могут перегореть, а последняя все равно будет работать.
Последовательные цепи
| Статьи о |
| Электромагнетизм |
|---|
 |
Последовательные цепи иногда называют связанными по току. Ток в последовательной цепи проходит через каждый компонент цепи. Таким образом, все компоненты в последовательном соединении проводят один и тот же ток.
Последовательная цепь имеет только один путь, по которому может течь ток. Размыкание или разрыв последовательной цепи в любой точке приводит к «размыканию» или прекращению работы всей цепи. Например, если хотя бы одна из лампочек в старой гирлянде рождественских елок перегорает или вынимается, вся гирлянда становится неработоспособной, пока не будет заменена неисправная лампочка.
Текущий
В последовательной цепи ток одинаков для всех элементов.
Напряжение
В последовательной цепи напряжение представляет собой сумму падений напряжения на отдельных элементах (единицах сопротивления).
Отряды сопротивления
Общее сопротивление двух или более резисторов, соединенных последовательно, равно сумме их индивидуальных сопротивлений:
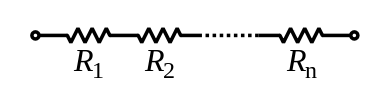 Здесь нижний индекс s в R s обозначает «серию», а R s обозначает сопротивление в серии.
Здесь нижний индекс s в R s обозначает «серию», а R s обозначает сопротивление в серии.
Проводимость
Электропроводность представляет собой величину, обратную сопротивлению. Полная проводимость последовательной цепи чистых сопротивлений, следовательно, может быть рассчитана по следующему выражению:
Для частного случая двух последовательных проводимостей общая проводимость равна:
Индукторы
Индукторы подчиняются тому же закону, что общая индуктивность не связанных последовательно индукторов равна сумме их индивидуальных индуктивностей:
Однако в некоторых ситуациях трудно предотвратить влияние соседних индукторов друг на друга, поскольку магнитное поле одного устройства связывается с обмотками его соседей. Это влияние определяется взаимной индуктивностью M. Например, если два индуктора соединены последовательно, то существуют две возможные эквивалентные индуктивности в зависимости от того, как магнитные поля обоих индукторов влияют друг на друга.
Когда имеется более двух индукторов, взаимная индуктивность между каждым из них и то, как катушки влияют друг на друга, усложняют расчет. Для большего числа катушек общая объединенная индуктивность определяется суммой всех взаимных индуктивностей между различными катушками, включая взаимную индуктивность каждой данной катушки с самой собой, которая называется самоиндукцией или просто индуктивностью. Для трех катушек существует шесть взаимных индуктивностей , , и , и . Существуют также три самоиндукции трех катушек: , и .
Поэтому
По принципу взаимности = так, чтобы последние две группы можно было объединить. Первые три члена представляют собой сумму самоиндукций различных катушек. Формула легко распространяется на любое количество последовательных катушек с взаимной связью. Метод может быть использован для нахождения самоиндукции больших катушек провода любой формы поперечного сечения путем вычисления суммы взаимной индуктивности каждого витка провода в катушке с каждым другим витком, поскольку в такой катушке все витки соединены последовательно.
Конденсаторы
Конденсаторы следуют тому же закону, используя обратные величины. Общая емкость конденсаторов, соединенных последовательно, равна обратной величине суммы обратных величин их индивидуальных емкостей:
Эквивалентно используя эластичность (величину, обратную емкости), общая последовательная эластичность равна сумме эластичностей каждого конденсатора.
Переключатели
Два или более переключателей последовательно образуют логическое И ; цепь проводит ток только в том случае, если все переключатели замкнуты. См. И-вентиль .
Элементы и батареи
Аккумулятор — это набор электрохимических ячеек . Если ячейки соединены последовательно, напряжение батареи будет равно сумме напряжений ячеек. Например, автомобильная батарея на 12 вольт содержит шесть 2-вольтовых ячеек, соединенных последовательно. Некоторые транспортные средства, такие как грузовики, имеют две 12-вольтовые батареи, соединенные последовательно, чтобы питать 24-вольтовую систему.
Параллельные цепи

Если два или более компонентов соединены параллельно, то они имеют одинаковую разность потенциалов (напряжение) на своих концах. Разности потенциалов на компонентах одинаковы по величине, и они также имеют одинаковую полярность. Одно и то же напряжение приложено ко всем компонентам цепи, соединенным параллельно. Общий ток является суммой токов через отдельные компоненты, в соответствии с законом токов Кирхгофа .
Напряжение
В параллельной цепи напряжение на всех элементах одинаково.
Текущий
Ток в каждом отдельном резисторе находится по закону Ома . Вынесение напряжения за скобки дает
Отряды сопротивления
Чтобы найти общее сопротивление всех компонентов, сложите обратные величины сопротивлений каждого компонента и возьмите обратную величину суммы. Общее сопротивление всегда будет меньше значения наименьшего сопротивления:
Для всего лишь двух сопротивлений невзаимное выражение достаточно простое:
Иногда это происходит с помощью мнемонического произведения суммы .
Для N одинаковых сопротивлений, соединенных параллельно, выражение обратной суммы упрощается до: и, следовательно, до:
Чтобы найти ток в компоненте с сопротивлением , снова воспользуемся законом Ома:
Компоненты делят ток в соответствии со своими обратными сопротивлениями, так, в случае двух резисторов,
Старый термин для устройств, подключенных параллельно, — «множественное» , например, множественные соединения для дуговых ламп .
Проводимость
Поскольку электропроводность обратно пропорциональна сопротивлению, выражение для полной проводимости параллельной цепи резисторов имеет простой вид:
Соотношения для полной проводимости и сопротивления находятся в дополнительных отношениях: выражение для последовательного соединения сопротивлений такое же, как и для параллельного соединения проводимостей, и наоборот.
Индукторы
Индукторы подчиняются тому же закону, что общая индуктивность несвязанных параллельно индукторов равна обратной величине суммы обратных величин их индивидуальных индуктивностей:
Если индукторы расположены в магнитных полях друг друга, этот подход недействителен из-за взаимной индуктивности. Если взаимная индуктивность между двумя параллельными катушками равна M , эквивалентный индуктор равен:
Если
Знак зависит от того, как магнитные поля влияют друг на друга. Для двух одинаковых плотно связанных катушек общая индуктивность близка к индуктивности каждой отдельной катушки. Если полярность одной катушки изменена так, что M отрицательна, то параллельная индуктивность близка к нулю или комбинация почти неиндуктивна. Предполагается, что в случае «плотной связи» M почти равна L. Однако, если индуктивности не равны и катушки плотно связаны, могут возникнуть близкие к короткому замыканию условия и высокие циркулирующие токи как для положительных, так и для отрицательных значений M , что может вызвать проблемы.
Более трех индукторов становятся более сложными, и необходимо учитывать взаимную индуктивность каждого индуктора относительно другого индуктора и их влияние друг на друга. Для трех катушек существует три взаимные индуктивности , и . Это лучше всего обрабатывается матричными методами и суммированием членов обратной матрицы (3×3 в данном случае).
Соответствующие уравнения имеют вид:
Конденсаторы
Общая емкость параллельно соединенных конденсаторов равна сумме их индивидуальных емкостей:
Рабочее напряжение параллельной комбинации конденсаторов всегда ограничено наименьшим рабочим напряжением отдельного конденсатора.
Переключатели
Два или более переключателей, соединенных параллельно, образуют логическое ИЛИ ; цепь проводит ток, если хотя бы один переключатель замкнут. См. элемент ИЛИ .
Элементы и батареи
Если ячейки батареи соединены параллельно, напряжение батареи будет таким же, как напряжение ячейки, но ток, подаваемый каждой ячейкой, будет составлять часть общего тока. Например, если батарея состоит из четырех идентичных ячеек, соединенных параллельно, и выдает ток 1 ампер , ток, подаваемый каждой ячейкой, будет составлять 0,25 ампера. Если ячейки не идентичны по напряжению, ячейки с более высоким напряжением будут пытаться зарядить ячейки с более низким, что может привести к их повреждению.
Параллельно соединенные батареи широко использовались для питания нитей накаливания в портативных радиоприемниках . Литий-ионные аккумуляторные батареи (особенно батареи ноутбуков) часто соединяются параллельно для увеличения номинала ампер-часов. Некоторые солнечные электрические системы имеют батареи, соединенные параллельно для увеличения емкости хранения; близкое приближение общего количества ампер-часов является суммой всех ампер-часов параллельно соединенных батарей.
Объединение проводимостей
Из законов Кирхгофа для цепей можно вывести правила объединения проводимостей. Для двух проводимостей и параллельно , напряжение на них одинаково и из закона тока Кирхгофа (KCL) общий ток равен
Подставляя закон Ома для проводимостей, получаем и эквивалентную проводимость,
Для двух проводимостей , соединенных последовательно, ток через них будет одинаковым, а закон напряжения Кирхгофа гласит, что напряжение на них равно сумме напряжений на каждой проводимости, то есть:
Подставляя закон Ома для проводимости, получаем, что в свою очередь дает формулу для эквивалентной проводимости:
Это уравнение можно немного перестроить, хотя это особый случай, который перестроится таким образом только для двух компонентов.
Для трех проводимостей, соединенных последовательно,
Обозначение
Значение двух параллельных компонентов часто представляется в уравнениях с помощью параллельного оператора , двух вертикальных линий (∥), заимствуя обозначение параллельных линий из геометрии .
Это упрощает выражения, которые в противном случае усложнялись бы расширением терминов. Например:
Приложения
Распространенное применение последовательной цепи в бытовой электронике — батареи, где несколько ячеек, соединенных последовательно, используются для получения удобного рабочего напряжения. Две одноразовые цинковые ячейки, соединенные последовательно, могут питать фонарик или пульт дистанционного управления при напряжении 3 вольта; аккумуляторная батарея для ручного электроинструмента может содержать дюжину литий-ионных ячеек, соединенных последовательно, для обеспечения 48 вольт.
Последовательные цепи ранее использовались для освещения в электропоездах . Например, если напряжение питания составляло 600 вольт, то могло быть восемь лампочек по 70 вольт последовательно (всего 560 вольт) плюс резистор для снижения оставшихся 40 вольт. Последовательные цепи для освещения поездов были заменены сначала мотор-генераторами , а затем твердотельными устройствами.
Последовательное сопротивление также может быть применено к расположению кровеносных сосудов в пределах данного органа. Каждый орган снабжается большой артерией, более мелкими артериями, артериолами, капиллярами и венами, расположенными последовательно. Общее сопротивление представляет собой сумму индивидуальных сопротивлений, как выражается следующим уравнением: R общее = R артерии + R артериол + R капилляров . Наибольшая доля сопротивления в этой серии приходится на артериолы. [3]
Параллельное сопротивление иллюстрируется кровеносной системой . Каждый орган снабжается артерией, которая ответвляется от аорты . Общее сопротивление этого параллельного расположения выражается следующим уравнением: 1/ R total = 1/ R a + 1/ R b + ... + 1/ R n . R a , R b и R n являются сопротивлениями почечной, печеночной и других артерий соответственно. Общее сопротивление меньше сопротивления любой из отдельных артерий. [3]
Смотрите также
- Антипараллельный (электроника)
- Объединение импедансов
- Делитель тока
- Эквивалентные преобразования импеданса
- Гидравлическая аналогия
- Анализ сетей (электрические цепи)
- Расстояние сопротивления
- Последовательно-параллельная дуальность
- Последовательно-параллельный частичный порядок
- Последовательные и параллельные пружины
- Топология (электрические цепи)
- Делитель напряжения
- мост Уитстона
- Преобразование Y-Δ
Ссылки
- ^ abc Резник, Роберт; Холлидей, Дэвид (1966). "Глава 32". Физика . Том I и II (Объединенное международное издание). Wiley . LCCN 66-11527. Пример 1.
- ^ Смит, Р. Дж. (1966). Схемы, приборы и системы (Международное издание). Нью-Йорк: Wiley . С. 21. LCCN 66-17612.
- ^ ab Костанцо, Линда С. Физиология . Серия обзоров совета. стр. 74.
Дальнейшее чтение
- Уильямс, Тим (2005). Спутник проектировщика схем . Баттерворт-Хайнеманн . ISBN 0-7506-6370-7.
- «Комбинации резисторов: сколько значений при использовании резисторов сопротивлением 1 кОм?». Журнал EDN .
- Гротц, Бернхард (04 января 2018 г.). «Стремунгширдерстенд». Mechanik der Flüssigkeiten (на немецком языке).