Параллельный (оператор)

Параллельный оператор (произносится как «параллельный», [1] следуя обозначению параллельных линий из геометрии ; [2] [3] также известный как сокращенная сумма , параллельная сумма или параллельное сложение ) — это бинарная операция , которая используется в качестве сокращения в электротехнике , [4] [5] [6] [примечание 1] но также используется в кинетике , механике жидкостей и финансовой математике . [7] [8] Название «параллельный» происходит от использования оператора, вычисляющего объединенное сопротивление резисторов, соединенных параллельно .
Обзор
Параллельный оператор представляет собой обратное значение суммы обратных значений (иногда также называемое «обратной формулой» или « гармонической суммой») и определяется следующим образом: [9] [6] [10] [11]
где a , b , и являются элементами расширенных комплексных чисел [12] [13]
Оператор дает половину гармонического среднего двух чисел a и b . [7] [8]
В качестве особого случая для любого числа :
Далее, для всех различных чисел :
с представлением абсолютного значения и означающим минимум ( наименьший элемент) среди x и y .
Если и — различные положительные действительные числа, то
Эта концепция была расширена от скалярной операции до матриц [14] [15] [16] [17] [18] и далее обобщена . [19]
Обозначение
Первоначально оператор был введен как сокращенная сумма Сундарамом Сешу в 1956 году [20] [21] [14], изучен как оператор ∗Кентом Э. Эриксоном в 1959 году [22] [23] [14] и популяризирован Ричардом Джеймсом Даффином и Уильямом Найлсом Андерсоном-младшим как оператор параллельного сложения или параллельной суммы: в математике и теории сетей с 1966 года. [15] [16] [1] Хотя некоторые авторы продолжают использовать этот символ до настоящего времени, [7] [8] например, Суджит Кумар Митра использовал его ∙как символ в 1970 году. [14] В прикладной электронике знак ∥стал более распространенным в качестве символа оператора около 1974 года. [24] [25] [26] [27] [28] [примечание 1] [примечание 2] Он часто записывался как двойная вертикальная линия (||), доступная в большинстве наборов символов (иногда курсивом как //[29] [30] ), но теперь может быть представлен с помощью символа Unicode U+2225 ( ∥ ) для «параллельно». В LaTeX и связанных языках разметки макросы \|и \parallelчасто используются (и редко \smallparallelиспользуются) для обозначения символа оператора.
Характеристики
Пусть представим расширенную комплексную плоскость, исключающую ноль, и биективную функцию от до такую, что One имеет тождества
и
Это немедленно подразумевает, что есть поле , в котором параллельный оператор занимает место сложения, и что это поле изоморфно
Следующие свойства могут быть получены путем перевода через соответствующие свойства комплексных чисел.
Свойства поля
Как и в любой области, удовлетворяет множеству основных идентичностей.
Он коммутативен относительно параллельности и умножения:
Ассоциативен относительно параллельности и умножения: [12] [7] [8]
Обе операции имеют элемент идентичности ; для параллельной операции идентичность равна 1 , а для умножения идентичность равна 1 :
Каждый элемент имеет обратный элемент по отношению к параллельному, равный аддитивному обратному элементу по отношению к сложению. (Но 0 не имеет обратного элемента по отношению к параллельному.)
Элемент идентичности является своим собственным обратным элементом,
Каждый элемент имеет мультипликативный обратный элемент :
Умножение является дистрибутивным по параллельности: [1] [7] [8]
Повторяющаяся параллель
Повторная параллель эквивалентна делению,
Или, умножив обе части на n ,
В отличие от повторного сложения , это не коммутирует:
Биномиальное разложение
Используя распределительное свойство дважды, произведение двух параллельных двучленов можно разложить как
Квадрат двучлена равен
Куб двучлена равен
В общем случае степень бинома n можно разложить с помощью биномиальных коэффициентов , которые являются обратными коэффициентами сложения, что приводит к аналогу формулы бинома :
Логарифм и экспонента
Имеют место следующие тождества:
Факторизация параллельных многочленов
Как и в случае с многочленом при сложении, параллельный многочлен с коэффициентами в (с ) можно разложить на множители в виде произведения одночленов:
для некоторых корней (возможно, повторяющихся) в
Аналогично полиномам при сложении, полиномиальное уравнение
подразумевает, что для некоторого k .
Квадратичная формула
Линейное уравнение можно легко решить с помощью параллельной обратной задачи:
Чтобы решить параллельное квадратное уравнение, дополните квадрат , чтобы получить аналог квадратной формулы
Включая ноль
Расширенные комплексные числа, включая ноль, больше не являются полем при параллельной обработке и умножении, поскольку 0 не имеет обратного значения при параллельной обработке. (Это аналогично тому, как не является полем, поскольку не имеет аддитивной обратной величины.)
Для каждого ненулевого a ,
Величину можно либо оставить неопределенной (см. неопределенную форму ), либо определить равной 0 .
Приоритет
При отсутствии скобок параллельный оператор определяется как имеющий приоритет над сложением или вычитанием, аналогично умножению. [1] [31] [9] [10]
Приложения
Параллельный оператор применяется в электронике, оптике и изучении периодичности:
Анализ схемы
В электротехнике параллельный оператор может использоваться для расчета полного сопротивления различных последовательных и параллельных электрических цепей. [nb 2] Существует двойственность между обычной (последовательной) суммой и параллельной суммой. [7] [8]
Например, общее сопротивление резисторов, соединенных параллельно, является величиной, обратной сумме обратных величин отдельных резисторов .
Аналогично для общей емкости последовательных конденсаторов . [nb 2]
Уравнение линзы
В геометрической оптике — приближение тонкой линзы к уравнению изготовителя линз.
Синодический период
Время между соединениями двух вращающихся тел называется синодическим периодом . Если период более медленного тела равен T 2 , а период более быстрого равен T 1 , то синодический период равен
Примеры
Вопрос:
- Три резистора соединены параллельно . Каково их результирующее сопротивление ?
Отвечать:
- Эффективное результирующее сопротивление составляет около 57 кОм .
Вопрос: [7] [8]
- Строитель возводит стену за 5 часов. Другому рабочему потребуется 7 часов на ту же работу. Сколько времени потребуется, чтобы построить стену, если оба рабочих будут работать параллельно?
Отвечать:
- Они закончат примерно через 3 часа.
Выполнение

Предложенный еще Кентом Э. Эриксоном в качестве подпрограммы в цифровых компьютерах в 1959 году [22] , параллельный оператор реализован как оператор клавиатуры на научных калькуляторах с обратной польской нотацией (RPN) WP 34S с 2008 года [32] [33] [34] , а также на WP 34C [35] и WP 43S с 2015 года [36] [37], что позволяет решать даже каскадные задачи несколькими нажатиями клавиш, например .270↵ Enter180∥120∥
Проекционный вид
Для данного поля F существуют два вложения F в проективную прямую P( F ): z → [ z : 1] и z → [1 : z ]. Эти вложения перекрываются, за исключением [0:1] и [1:0]. Параллельный оператор связывает операцию сложения между вложениями. Фактически, гомографии на проективной прямой представлены матрицами 2 x 2 M(2, F ), а полевые операции (+ и ×) распространяются на гомографии. Каждое вложение имеет свое сложение a + b, представленное следующими умножениями матриц в M(2, A ):
Два матричных произведения показывают, что существуют две подгруппы M(2, F ), изоморфные ( F ,+), аддитивной группе F . В зависимости от того, какое вложение используется, одна операция — +, другая —
Примечания
- ^ ab Хотя использование символа ∥ для обозначения «параллельного» в геометрии восходит к 1673 году в работе Джона Керси-старшего , [A] он стал более широко использоваться только с 1875 года. [B] Использование математического оператора для параллельных цепей берет свое начало в теории сетей в электротехнике . Сундарам Сешу ввел оператор сокращенной суммы в 1956 году, [C] Кент Э. Эриксон предложил звездочку (∗) для обозначения оператора в 1959 году, [D] в то время как Ричард Джеймс Даффин и Уильям Найлс Андерсон-младший использовали двоеточие ( :) для параллельного сложения с 1966 года. [E] Суджит Кумар Митра использовал для него точку (∙) в 1970 году. [F] Первое использование параллельного символа (∥) для этого оператора в прикладной электронике неизвестно, но, возможно, оно возникло в книге Стивена Д. Сентурии и Брюса Д. Уэдлока 1974 года «Электронные схемы и приложения», [G], которая развилась из их вводного курса по электронике в Массачусетском технологическом институте (MIT) с концепциями преподавания теории сетей и электроники, заимствованными из более раннего курса, который читал Кэмпбелл «Кэм» Лич Сирл. Он получил дальнейшую популяризацию благодаря книге Джона У. Маквейна 1981 года «Введение в электронику и приборостроение» [H] , которая выросла из одноименного курса Массачусетского технологического института, разработанного в рамках влиятельного Проекта по разработке технических учебных программ между 1974 и 1979 годами. Этот символ, вероятно, был введен также потому, что другие используемые символы можно было легко спутать со знаками, обычно используемыми для умножения и деления в некоторых контекстах.
- ^ abc В электрических цепях параллельный оператор может применяться к параллельным сопротивлениям ( R в [Ω]) или индуктивностям ( L в [H]), а также к импедансам ( Z в [Ω]) или реактивным сопротивлениям ( X в [Ω]). Игнорируя вводящий в заблуждение глиф символа оператора , его также можно применять к последовательным цепям, соответственно, проводимостей ( G в [S]) или емкостей ( C в [F]), а также проводимостей ( Y в [S]) или реактивных проводимостей ( B в [S]).
Ссылки
- ^ abcd Даффин, Ричард Джеймс (1971) [1970, 1969]. "Модели сетей". Написано в Дареме, Северная Каролина, США. В Wilf, Herbert Saul ; Hararay, Frank (ред.). Математические аспекты анализа электрических сетей. Труды симпозиума по прикладной математике Американского математического общества и Общества промышленной и прикладной математики, состоявшегося в Нью-Йорке, 1969-04-02/03. Том III Трудов SIAM-AMS (иллюстрированное издание). Провиденс, Род-Айленд: Американское математическое общество (AMS) / Общество промышленной и прикладной математики (SIAM). стр. 65–92 [68]. ISBN 0-8218-1322-6. ISSN 0080-5084. LCCN 79-167683. ISBN 978-0-8218-1322-5 . Отчет 69-21 . Получено 05.08.2019 . стр. 68– 69:
[…] Чтобы иметь удобную краткую запись для совместного сопротивления резисторов, соединенных параллельно, пусть […] A:B = AB/(A+B) […] A:B можно рассматривать как новую операцию, называемую
параллельным сложением
[…] Параллельное сложение определено для любых неотрицательных чисел. Сетевая модель показывает, что параллельное сложение
коммутативно
и
ассоциативно
. Более того, умножение является
дистрибутивным
относительно этой операции. Рассмотрим теперь алгебраическое выражение с операциями (+) и (:), действующими на положительных числах A, B, C и т. д. […] Чтобы дать сетевую интерпретацию такого многочлена, прочитайте
A + B
как «A ряд B» и
A : B
как «A параллельный B», тогда ясно, что выражение […] является совместным сопротивлением сети […]
[1] [2] (206 страниц)
- ^ Керси (старший), Джон (1673). «Глава I: О сфере действия этой четвертой книги и значении используемых в ней символов, сокращений и цитат». Элементы этого математического искусства, обычно называемого алгеброй. Том. Книга IV — Элементы алгебраических искусств. Лондон: Thomas Passinger, Three-Bibles, London-Bridge. стр. 177–178 . Архивировано из оригинала 05.08.2020 . Получено 09.08.2019 .
- ^ Cajori, Florian (1993) [сентябрь 1928]. "§ 184, § 359, § 368". История математических обозначений – обозначения в элементарной математике. Том 1 (два тома в одном неизмененном переиздании). Чикаго, США: Open court Publishing Company . стр. 193, 402–403, 411–412. ISBN 0-486-67766-4. LCCN 93-29211 . Получено 22.07.2019 . стр. 402– 403, 411– 412:
§359. […] ∥ для параллельности встречается в Opuscula mathematica hactenus inedita (1677) [стр. 197], посмертной работе Отреда (§ 184) […] §368. Знаки для параллельных линий. […] когда знак равенства Рекорда завоевал свое место на континенте , вертикальные линии стали использоваться для обозначения параллельности. Мы находим ∥ для «параллельного» у Керси , [A] Касвелла , Джонса , [B] Уилсона, [C] Эмерсона , [D] Камбли, [E] и авторов последних пятидесяти лет, которые уже цитировались в связи с другими пиктограммами. Примерно до 1875 года это встречалось не так часто […] Холл и Стивенс [F] использовали «par [F] или ∥» для обозначения параллельного […][A] Джон Керси , Алгебра (Лондон, 1673), Книга IV, стр. 177.[B] У. Джонс , Synopsis palmarioum matheseos (Лондон, 1706 г.).[C] Джон Уилсон, Тригонометрия (Эдинбург, 1714), объяснение символов.[D] У. Эмерсон , Элементы геометрии (Лондон, 1763), стр. 4.[E] Л. Камбли , Die Elementar-Mathematik , Часть 2: Planimetrie , 43. издание (Бреслау, 1876), с. 8. […][F] Х. С. Холл и Ф. Х. Стивенс, «Начала Евклида» , части I и II (Лондон, 1889), стр. 10. […]
[3] - ^ "INA 326/INA 327 – Precision, Rail-to-Rail I/O Instrumentation Amplifier" (PDF) . Burr-Brown / Texas Instruments . 2018 [ноябрь 2004 г., ноябрь 2001 г.]. стр. 3, 9, 13. SBOS222D. Архивировано (PDF) из оригинала 2019-07-13 . Получено 2019-07-13 .
- ^ Бобер, Уильям; Стивенс, Эндрю (2016). "Глава 7.6. Преобразования Лапласа, применяемые к схемам". Численные и аналитические методы с MATLAB для инженеров-электриков. Прикладная и вычислительная механика (1-е изд.). CRC Press . стр. 224. ISBN 978-1-46657607-0. ISBN 1-46657607-3 . (388 страниц)
- ^ ab Ranade, Gireeja; Stojanovic, Vladimir, eds. (осень 2018 г.). "Глава 15.7.2 Параллельные резисторы" (PDF) . EECS 16A Проектирование информационных устройств и систем I (PDF) (конспекты лекций). Калифорнийский университет, Беркли . стр. 12. Примечание 15. Архивировано (PDF) из оригинала 2018-12-27 . Получено 2018-12-28 . стр. 12:
[…] Это математическое соотношение встречается достаточно часто, чтобы у него даже было название: "параллельный оператор", обозначаемый ∥. Когда мы говорим x∥y, это означает
. Обратите внимание, что это математический оператор, и он ничего не говорит о фактической конфигурации. В случае резисторов параллельный оператор используется для параллельных резисторов, но для других компонентов (например, конденсаторов) это
не
так. […]
(16 страниц)
- ^ abcdefg Эллерман, Дэвид Паттерсон (1995-03-21). "Глава 12: Параллельное сложение, последовательно-параллельная дуальность и финансовая математика". Интеллектуальное вторжение как образ жизни: очерки по философии, экономике и математике (PDF) . Мирская философия: исследования на стыке философии и экономики (иллюстрированное издание). Rowman & Littlefield Publishers, Inc. стр. 237–268 . ISBN 0-8476-7932-2. Архивировано (PDF) из оригинала 2016-03-05 . Получено 2019-08-09 . стр. 237:
[…] Когда резисторы с сопротивлением a и b расположены последовательно, их составное сопротивление представляет собой обычную сумму (далее — последовательная сумма ) сопротивлений a + b. Если сопротивления расположены параллельно, их составное сопротивление представляет собой параллельную сумму сопротивлений, которая обозначается полным двоеточием […]
[4] (271 страница) - ^ abcdefg Эллерман, Дэвид Паттерсон (май 2004 г.) [1995-03-21]. "Введение в последовательно-параллельную дуальность" (PDF) . Калифорнийский университет в Риверсайде . CiteSeerX 10.1.1.90.3666 . Архивировано из оригинала 2019-08-10 . Получено 2019-08-09 .
Параллельная сумма двух положительных действительных чисел x:y = [(1/x) + (1/y)]
−1
возникает в теории электрических цепей как сопротивление, возникающее при параллельном соединении двух сопротивлений x и y. Существует
дуальность
между обычной
(последовательной) суммой
и параллельной суммой. […]
[5] (24 страницы)
- ^ ab Basso, Christophe P. (2016). "Глава 1.1.2 Текущий делитель". Линейные передаточные функции цепей: Введение в быстрые аналитические методы (1-е изд.). Чичестер, Западный Сассекс, Нью-Джерси, США: John Wiley & Sons Ltd. стр. 12. ISBN 978-1-11923637-5. LCCN 2015047967 . Получено 28.12.2018 .(464 страницы)
- ^ ab Cotter, Neil E., ред. (12.10.2015) [20.09.2014]. "ECE1250 Cookbook – Nodes, Series, Parallel" (конспекты лекций). Cookbooks. University of Utah . Архивировано (PDF) из оригинала 20.08.2020 . Получено 11.08.2019 .
[…] Один из удобных способов указать, что два резистора соединены параллельно, — поставить между ними знак ∥. […]
- ^ Бёккер, Иоахим (18 марта 2019 г.) [апрель 2008 г.]. «Grundlagen der Elektrotechnik Teil B» (PDF) (на немецком языке). Университет Падерборна . п. 12. Архивировано (PDF) из оригинала 17 апреля 2018 г. Проверено 9 августа 2019 г. п. 12:
Für die Berechnung des Ersatzwiderstands der Parallelschaltung wird […] gern die Kurzschreibweise ∥ benutzt.
- ^ аб Георг, Отфрид (2013) [1999]. «Глава 2.11.4.3: Aufstellen der Differentialgleichung aus der komplexen Darstellung - MATHCAD Anwendung 2.11-6: Benutzerdefinierte Operatingen». Elektromagnetische Felder und Netzwerke: Anwendungen в Mathcad и PSpice. Springer-Lehrbuch (на немецком языке) (1-е изд.). Спрингер-Верлаг . стр. 246–248 . doi : 10.1007/978-3-642-58420-6. ISBN 978-3-642-58420-6. ISBN 3-642-58420-9 . Получено 04.08.2019 . (728 страниц)
- ^
 Ассоциативная композиция алгебры/Гомографии в Wikibooks
Ассоциативная композиция алгебры/Гомографии в Wikibooks - ^ abcd Mitra, Sujit Kumar (февраль 1970 г.). "Матричная операция для анализа последовательно-параллельных многопортовых сетей". Журнал Института Франклина . Краткое сообщение. 289 (2). Институт Франклина : 167– 169. doi :10.1016/0016-0032(70)90302-9. стр. 167:
Целью этого сообщения является распространение концепции
скалярной
операции Приведенная сумма, введенной Сешу […] и позднее разработанной Эриксоном […], на матрицы, чтобы описать некоторые интересные свойства этой новой матричной операции и применить матричную операцию в анализе последовательных и параллельных
n
-портовых сетей
. Пусть A и B — две невырожденные
квадратные матрицы,
имеющие
обратные
, A
−1
и B
−1
соответственно. Операцию ∙ мы определяем как A ∙ B = (A
−1
+ B
−1
)
−1
, а операцию ⊙ как A ⊙ B = A ∙ (−B). Операция ∙ является
коммутативной
и
ассоциативной
, а также
дистрибутивной
относительно умножения. […]
(3 страницы)
- ^ ab Даффин, Ричард Джеймс ; Хазони, Дов; Моррисон, Норман Александр (март 1966) [1965-04-12, 1964-08-25]. "Синтез сетей с помощью гибридных матриц". Журнал SIAM по прикладной математике . 14 (2). Общество промышленной и прикладной математики (SIAM): 390– 413. doi :10.1137/0114032. JSTOR 2946272.(24 страницы)
- ^ ab Anderson, Jr., William Niles; Duffin, Richard James (1969) [1968-05-27]. "Последовательное и параллельное сложение матриц". Journal of Mathematical Analysis and Applications . 26 (3). Academic Press, Inc. : 576– 594. doi : 10.1016/0022-247X(69)90200-5 . p. 576:
[…] мы определяем параллельную сумму A и B формулой A(A + B)
+
B и обозначаем ее как A : B. Если A и B невырожденны, это сводится к A : B = (A
−1
+ B
−1
)
−1
, которая является хорошо известной электрической формулой для сложения резисторов параллельно. Затем показано, что
эрмитовы
полуопределенные матрицы образуют
коммутативную
частично упорядоченную полугруппу относительно операции параллельной суммы. […]
[6]
- ^ Митра, Суджит Кумар; Пури, Мадан Лал (октябрь 1973 г.). «О параллельной сумме и разности матриц» (PDF) . Журнал математического анализа и приложений . 44 (1). Academic Press, Inc .: 92– 97. doi :10.1016/0022-247X(73)90027-9. Архивировано из оригинала (PDF) 2019-04-13.
- ^ Митра, Суджит Кумар; Бхимасанкарам, Почираджу; Малик, Сародж Б. (2010). Матричные частичные порядки, сокращенные операторы и приложения. Серия по алгебре. Том 10 (иллюстрированное 1-е изд.). World Scientific Publishing Co. Pte. Ltd. ISBN 978-981-283-844-5. ISBN 981-283-844-9 . Получено 19 августа 2019 г. . (446 страниц)
- ^ Эрикссон-Бике, Сиркка-Лииза Аннели [на финском языке] ; Лейтвилер, Хайнц (февраль 1989 г.) [10 января 1989 г.]. «Обобщение параллельного сложения» (PDF) . Математические уравнения . 38 (1). Birkhäuser Verlag : 99–110 . doi : 10.1007/BF01839498. Архивировано (PDF) из оригинала 20 августа 2020 г. Проверено 20 августа 2020 г.
- ^ Seshu, Sundaram (сентябрь 1956). «Об электрических цепях и коммутационных цепях». Труды IRE по теории цепей . CT-3 (3). Институт радиоинженеров (IRE): 172– 178. doi :10.1109/TCT.1956.1086310.(7 страниц) (Примечание. См. исправления.)
- ^ Seshu, Sundaram; Gould, Roderick (сентябрь 1957 г.). "Исправление к 'On Electrical Circuits and Switching Circuits'". Труды IRE по теории цепей . Исправление. CT-4 (3). Институт радиоинженеров (IRE): 284. doi : 10.1109/TCT.1957.1086390 .(1 страница) (Примечание. Ссылка на предыдущую ссылку.)
- ^ ab Erickson, Kent E. (март 1959 г.). "Новая операция для анализа последовательно-параллельных сетей". IRE Transactions on Circuit Theory . CT-6 (1). Institute of Radio Engineers (IRE): 124– 126. doi :10.1109/TCT.1959.1086519. стр. 124:
[…] Операция ∗ определяется как A ∗ B = AB/A + B. Символ ∗ обладает алгебраическими свойствами, которые упрощают формальное решение многих задач последовательно-параллельной сети. Если бы операция ∗ была включена в качестве подпрограммы в
цифровой компьютер
, она могла бы упростить программирование определенных сетевых вычислений. […]
(3 страницы) (Примечание. См. комментарий.)
- ^ Кауфман, Говард (июнь 1963 г.). «Замечание о новой операции для анализа последовательно-параллельных сетей». Труды IEEE по теории цепей . CT-10 (2). Институт инженеров по электротехнике и электронике (IEEE): 283. doi :10.1109/TCT.1963.1082126. стр. 283:
[…] Комментарии к операции ∗ […] a∗b = ab/(a+b) […]
(1 страница) (Примечание. Ссылка на предыдущую ссылку.) - ^ Senturia, Stephen D. [на Wikidata] ; Wedlock, Bruce D. (1975) [август 1974]. "Часть A. Изучение языка, Глава 3. Линейные резистивные сети, 3.2 Базовые конфигурации сетей, 3.2.3. Параллельные резисторы". Написано в Массачусетском технологическом институте, Кембридж, Массачусетс, США. Electronic Circuits and Applications (1-е изд.). Нью-Йорк, Лондон, Сидней, Торонто: John Wiley & Sons, Inc. стр. viii– ix, 44–46 [45]. ISBN 0-471-77630-0. LCCN 74-7404. S2CID 61070327. стр. viii, ix, 45:
Этот учебник развился из односеместрового вводного курса по электронике, который авторы читали в Массачусетском технологическом институте . […] Курс используется многими первокурсниками в качестве предшественника основной программы по электротехнике Массачусетского технологического института. […] Подготовка книги такого размера потребовала вклада многих людей. Концепция преподавания теории сетей и электроники как единого объединенного предмета исходит от профессора Кэмпбелла Сирла, который преподавал вводный курс по электронике, когда один из нас (SDS) был аспирантом первого года обучения по физике, пытавшимся изучить электронику. Кроме того, профессор Сирл предоставил бесценную конструктивную критику на протяжении всего написания этого текста. Несколько членов факультета MIT и около 40 технических ассистентов приняли участие в преподавании этого материала за последние пять лет, многие из которых внесли важный вклад своими предложениями и примерами. Среди них мы особенно хотим поблагодарить OR Mitchell, Irvin Englander, George Lewis, Ernest Vincent, David James, Kenway Wong, Gim Hom, Tom Davis, James Kirtley и Robert Donaghey. Председатель кафедры электротехники MIT, профессор Louis D. Smullin , оказал поддержку и воодушевление в ходе этого проекта, как и многие коллеги по кафедре. […] Первый результат […] гласит, что общее напряжение на параллельной комбинации R 1 и R 2 такое же, как и на одном сопротивлении величиной R 1 R 2 (R 1 + R 2 ). Поскольку это выражение для параллельного сопротивления встречается так часто, ему дано специальное обозначение (R 1 ∥R 2 ). То есть, когда R 1 и R 2 соединены параллельно, эквивалентное сопротивление равно […]
(xii+623+5 страниц) (Примечание. Также было доступно руководство для учителя. Ранние тиражи содержат значительное количество типографских ошибок. См. также: Книга Уэдлока 1978 года.) [7] - ^ Wolf, Lawrence J. (1977) [1976, 1974]. «Раздел 4. Учебные материалы – 4.3. Проект по разработке технической учебной программы MIT – Введение в электронику и приборостроение». В Aldridge, Bill G.; Mowery, Donald R.; Wolf, Lawrence J.; Dixon, Peggy (ред.). Science and Engineering Technology – Curriculum Guide: A Guide to a Two-Year Associate Degree Curriculum (PDF) . Saint Louis Community College–Florissant Valley , St. Louis, Missouri, USA: National Science Teachers Association , Washington DC, USA. стр. 21, 77. Архивировано (PDF) из оригинала 2017-02-15 . Получено 2019-08-08 . стр. 21:
[…] Введение в электронику и приборостроение — это новый и современный подход к вводному курсу по электронике. Разработанный для студентов без предварительного опыта работы с электроникой, он развивает навыки и знания, необходимые для использования и понимания современных электронных систем. […] Джон В. МакВейн […]
(Примечание. Проект SET представлял собой двухгодичную программу обучения после окончания средней школы, разработанную в период с 1974 по 1977 год и готовившую техников к использованию электронных приборов.) - ^ Wiesner, Jerome Bert ; Johnson, Howard Wesley ; Killian, Jr., James Rhyne , ред. (1978-04-11). «Школа инженерии – Центр передовых инженерных исследований (CAES) – Исследования и разработки – Проект исследований и разработок технической учебной программы». Отчет президента и канцлера 1977–78 гг. – Массачусетский технологический институт (PDF) . Массачусетский технологический институт (MIT). стр. 249, 252–253 . Архивировано (PDF) из оригинала 2015-09-10 . Получено 2019-08-08 . стр. 249, 252–253 :
[…] Программа исследований и разработок технической учебной программы, спонсируемая Императорской организацией социальных служб
Ирана
,
вступает в четвертый год пятилетнего контракта. Продолжается разработка учебной программы по электронике и машиностроению. […] Проект, совместно администрируемый
CAES
и
кафедрой материаловедения и инженерии
, находится под руководством профессора Мертона К. Флемингса. Руководит им доктор Джон В. Маквейн. […] Разработка учебных материалов. Это основная деятельность проекта, которая связана с разработкой инновационных, современных учебных материалов в необходимых областях инженерных технологий […] новый вводный курс по электронике […] называется «Введение в электронику и приборостроение» и состоит из восьми […] модулей […] Постоянный ток, напряжение и сопротивление; Базовые схемы; Изменяющиеся во времени сигналы; Операционные усилители; Источники питания; Переменный ток, напряжение и импеданс; Цифровые схемы; и Электронные измерения и управление. Этот курс представляет собой существенное изменение и обновление способа введения электроники и должен иметь большую ценность для
STI,
а также для многих программ США. […]
- ^ Wedlock, Bruce D. (1978). Базовые схемы сетей . Введение в электронику и приборостроение. Массачусетский технологический институт (MIT), Проект исследований и разработок технической учебной программы.(81 страница) (Примечание. Это легло в основу Части I книги Маквейна 1981 года. См. также: Книга Сентурии и Уэдлока 1975 года.)
- ^ Маквейн, Джон У. (1981-05-01). Введение в электронику и приборостроение (иллюстрированное издание). North Scituate, Массачусетс, США: Breton Publishers , Wadsworth, Inc. стр. 78, 96– 98, 100, 104. ISBN 0-53400938-7. ISBN 978-0-53400938-0 . Получено 04.08.2019 . стр. xiii, 96–98, 100:
[…] Брюс Д. Уэдлок […] был основным автором, внесшим вклад в Часть I, БАЗОВЫЕ ЦЕПНЫЕ СЕТИ, включая разработку сопутствующих примеров. […] Большая часть разработки программы IEI была проведена в рамках Проекта исследований и разработок технической учебной программы Центра
передовых инженерных исследований Массачусетского технологического института
. […] сокращенное обозначение […] сокращенный символ ∥ […]
(xiii+545 страниц) (Примечание. В 1981 году также существовало 216-страничное лабораторное руководство, прилагавшееся к этой книге. Работа выросла из программы курса MIT «Проект по разработке технического учебного плана MIT — Введение в электронику и приборостроение», разработанной между 1974 и 1979 годами. В 1986 году было опубликовано второе издание этой книги под названием «Введение в электронную технологию».)
- ^ "7.5.3 Выбор внешнего сопротивления". TPL5110 Nano-Power System Timer for Power Gating (PDF) (Технический паспорт). Редакция A. Texas Instruments Incorporated . Сентябрь 2018 г. [Январь 2015 г.]. С. 13–14 . SNAS650A. Архивировано (PDF) из оригинала 2022-09-25 . Получено 2022-09-25 .(27 страниц)
- ^ "A7987: 61 В, 3 А асинхронный понижающий импульсный регулятор с регулируемым ограничением тока для автомобильной промышленности" (PDF) (Технический паспорт). Редакция 3. STMicroelectronics NV . 2020-09-22 [2019-03-19]. стр. 17, 18, 20. DS12928. Архивировано (PDF) из оригинала 2022-07-18 . Получено 2022-07-18 .(36 страниц)
- ^ Пол, Штеффен; Пол, Рейнхольд (24 октября 2014 г.). «Глава 2.3.2: Zusammenschaltungen линейное резистивное устройство Zweipole – Parallelschaltung». Grundlagen der Elektrotechnik und Elektronik 1: Gleichstromnetzwerke und ihre Anwendungen (на немецком языке). Том. 1 (5-е изд.). Спрингер-Верлаг . п. 78. ИСБН 978-3-64253948-0. ISBN 3-64253948-3 . Проверено 4 августа 2019 г. п. 78:
[…] Bei abgekürzter Schreibweise achte man sorgfältig auf die Anwendung von Klammern. […] Das Parallelzeichen ∥ der Kurzschreibweise Hat die gleiche Bedeutung wie ein Multiplikationszeichen. Дешалб кённен Кламмерн упал.
(446 страниц) - ^ Дейл, Пол; Бонин, Уолтер (2012-11-30) [2008-12-09]. Руководство пользователя WP 34S (PDF) (3.1 ред.). стр. 1, 14, 32, 66, 116. Архивировано (PDF) из оригинала 2019-07-09 . Получено 2019-07-13 .[8] (211 страниц)
- ^ Бонин, Уолтер (2015) [2008-12-09]. Руководство пользователя WP 34S (3.3 ред.). CreateSpace Independent Publishing Platform . ISBN 978-1-5078-9107-0.[9]
- ^ Бонин, Уолтер (2016-07-11) [2008-12-09]. Руководство пользователя WP 34S (4-е изд.). CreateSpace Independent Publishing Platform . ISBN 978-1-53366238-5. ISBN 1-53366238-X . (410 страниц)
- ^ Dowrick, Nigel (2015-05-03) [2015-03-16]. "Complex Lock mode for WP-34s". Музей HP . Архивировано из оригинала 2019-04-03 . Получено 2019-08-07 .
- ^ Бонин, Уолтер (2020) [2015]. Руководство пользователя WP 43S (PDF) . 0.16 (черновая редакция). стр. 119. ISBN 978-1-72950098-9. ISBN 1-72950098-6 . Архивировано (PDF) из оригинала 2022-07-21 . Получено 2020-08-20 . [10] [11] (328 страниц)
- ^ Бонин, Уолтер (2020) [2015]. Справочное руководство WP 43S (PDF) . 0.16 (черновая редакция). стр. 127. ISBN 978-1-72950106-1. ISBN 1-72950106-0 . Архивировано (PDF) из оригинала 2022-07-21 . Получено 2020-08-20 . [12] [13] (315 страниц)
Дальнейшее чтение
- Пекарев, Эдвард Л.; Шмульян, Ю. Л. (1976-04-30). «Параллельное сложение и параллельное вычитание операторов». Математика СССР-Известия . 10 (2). Американское математическое общество : 351– 370. Bibcode : 1976IzMat..10..351P. doi : 10.1070/IM1976v010n02ABEH001694.
- Даффин, Ричард Джеймс ; Морли, Том Д. (июль 1978 г.). «Почти определенные операторы и электромеханические системы». Журнал SIAM по прикладной математике . 35 (1). Общество промышленной и прикладной математики (SIAM): 21– 30. doi :10.1137/0135003. JSTOR 2101028.(10 страниц)
- Morley, Tom D. (июль 1979). "Parallel Summation, Maxwell's Principle and the Infimum of Projections" (PDF) . Journal of Mathematical Analysis and Applications . 70 (1). Department of Mathematics, University of Illinois at Urbana-Champaign , Urbana, Illinois, USA: 33– 41. doi :10.1016/0022-247X(79)90073-8. Архивировано из оригинала 20.08.2020 . Получено 20.08.2020 .
- Сигер, Альберто (май 1990 г.) [1988-03-22]. "Прямое и обратное сложение в выпуклом анализе и его приложениях" (PDF) . Журнал математического анализа и приложений . 148 (2). Кафедра математики, Вашингтонский университет , Сиэтл, Вашингтон, США: Academic Press, Inc. : 317– 349. doi :10.1016/0022-247X(90)90004-Y. Архивировано (PDF) из оригинала 20-08-2020 . Получено 20-08-2020 .(33 страницы)
- Bryant, Randal E. ; Tygar, J. Doug; Huang, Lawrence P. (1994). "Геометрическая характеристика последовательно-параллельных переменных резисторных цепей" (PDF) . IEEE Transactions on Circuits and Systems I: Fundamental Theory and Applications . 41 (11): 686– 698. doi :10.1109/81.331520. Архивировано из оригинала (PDF) 2017-08-14.
- Antezana, Jorge; Corach, Gustavo; Stojanoff, Demetrio (апрель 2006 г.) [2005-09-14]. "Bilateral Shorted Operators and Parallel Sums" (PDF) . Linear Algebra and Its Applications . 414 ( 2– 3). La Plata, Argentina & Buenos Aires, Argentina: 570– 588. arXiv : math/0509327 . doi :10.1016/j.laa.2005.10.039. Архивировано (PDF) из оригинала 2017-08-09 . Получено 2020-08-20 .[14] (19 страниц)
- Chansangiam, Pattrawut (февраль 2016 г.) [август 2015 г., июль 2015 г.]. «Математические аспекты электрических сетевых соединений». Инженерный журнал KKU . 43 (1): 47– 54. doi :10.14456/kkuenj.2016.8. Архивировано (PDF) из оригинала 20-08-2020 . Получено 20-08-2020 .
- Бесеньей, Адам (01 сентября 2016 г.). «Непреодолимое неравенство Милна» (PDF) . Будапешт: Департамент прикладного анализа и вычислительной математики, Университет Этвеша Лоранда . ЦРУ2016. Архивировано (PDF) из оригинала 8 августа 2019 г. Проверено 11 августа 2019 г.
- "7.5 Электрические характеристики: VCC = 5 В / 7.6 Электрические характеристики: VCC = 2,7 В / 9.1.2.1 Инвертирующий компаратор с гистерезисом". TLV3201, TLV3202: TLV320x 40-нс, microPOWER, двухтактные выходные компараторы (PDF) . Редакция B. Даллас, Техас, США: Texas Instruments Incorporated . 2022-06-03 [2016, 2012]. стр. 5, 6, 13–14 [13]. SBOS561B. Архивировано (PDF) из оригинала 2022-08-17 . Получено 2022-08-18 . стр. 5:
ПАРАМЕТР […] ТИП […] ЕДИНИЦА […] ВХОДНОЕ СОПРОТИВЛЕНИЕ […] Синфазный режим […] 10 13 ∥ 2 […] Ω ∥ пФ […] Дифференциальный […] 10 13 ∥ 4 […] Ω ∥ пФ […]
(37 страниц) (Примечание. Необычное использование ∥ как для значений, так и для единиц.)
Внешние ссылки
- https://github.com/microsoftarchive/edx-platform-1/blob/master/common/lib/calc/calc/calc.py























![{\displaystyle {\begin{align}a\parallel b&=b\parallel a\\[3mu]ab&=ba\end{align}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/33fdcf548e5e335be871903cc2d0cc02147439db)













![{\displaystyle {\begin{align}(a\parallel b)(c\parallel d)&=a(c\parallel d)\parallel b(c\parallel d)\\[3mu]&=ac\parallel ad\parallel bc\parallel bd.\end{align}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/75796fff00982215ddf28125ac13967f56303ac6)
![{\displaystyle {\begin{align}(a\parallel b)^{2}&=a^{2}\parallel ab\parallel ba\parallel b^{2}\\[3mu]&=a^{2}\parallel {\tfrac {1}{2}}ab\parallel b^{2}.\end{align}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5cc365e2090c31a9a827d434b9def70074105726)












![{\displaystyle {\begin{aligned}ax\parallel b&=\infty \\[3mu]\implies x&=-{\frac {b}{a}}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9f17b63944689d920e5fe583a2faa06bad488bc9)
![{\displaystyle {\begin{aligned}ax^{2}\parallel bx\parallel c&=\infty \\[5mu]x^{2}\parallel {\frac {b}{a}}x&=-{\frac {c}{a}}\\[5mu]x^{2}\parallel {\frac {b}{a}}x\parallel {\frac {4b^{2}}{a^{2}}}&=\left(-{\frac {c}{a}}\right)\parallel {\frac {4b^{2}}{a^{2}}}\\[5mu]\left(x\parallel {\frac {2b}{a}}\right)^{2}&={\frac {b^{2}\parallel -{\tfrac {1}{4}}ac}{{\tfrac {1}{4}}a^{2}}}\\[5mu]\подразумевает x&={\frac {(-b)\parallel \pm {\sqrt {b^{2}\parallel -{\tfrac {1}{4}}ac}}}{{\tfrac {1}{2}}a}}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/499ed1736b0e0cf7cea1e6de3291ffaacb848cfe)




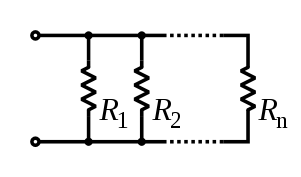
![{\displaystyle {\begin{aligned}{\frac {1}{R_{\text{eq}}}}&={\frac {1}{R_{1}}}+{\frac {1}{R_{2}}}+\cdots +{\frac {1}{R_{n}}}\\[5mu]R_{\text{eq}}&=R_{1}\параллельно R_{2}\параллельно \cdots \параллельно R_{n}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/92fddb4b991c03b156b12dd85c3cca8c3a3f66c1)





![{\displaystyle {\begin{aligned}R_{1}\parallel R_{2}\parallel R_{3}&=270\,\mathrm {k\Omega } \parallel 180\,\mathrm {k\Omega } \ параллель 120\,\mathrm {k\Omega } \\[5mu]&={\frac {1}{{\dfrac {1}{270\,\mathrm {k\Omega } }}+{\dfrac {1}{180\,\mathrm {k\Omega } }}+{\dfrac {1} {120\,\mathrm {k\Omega } }}}}\\[5mu]&\approx 56,84\,\mathrm {k\Омега } \end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8635ca3fd9bb42d8a264124fe968db472bb0486d)

![{\displaystyle {\begin{aligned}{\begin{pmatrix}1&0\\a&1\end{pmatrix}}{\begin{pmatrix}1&0\\b&1\end{pmatrix}}&={\begin{pmatrix}1&0\\a+b&1\end{pmatrix}},\\[10mu]{\begin{pmatrix}1&a\\0&1\end{pmatrix}}{\begin{pmatrix}1&b\\0&1\end{pmatrix}}&={\begin{pmatrix}1&a+b\\0&1\end{pmatrix}}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7a775bf62a63081caef53f3f33667ce290bbc4f5)



